↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Continual Learning (CL) faces a trade-off between preserving old knowledge and learning new tasks, often leading to catastrophic forgetting. Existing CL approaches struggle to balance both effectively. This paper addresses this challenge by introducing a novel perspective focusing on model parameter sensitivity. Excessive sensitivity causes significant forgetting and overfitting.
This paper proposes Model Sensitivity Aware Continual Learning (MACL), which addresses CL by optimizing model performance considering the worst-case parameter distribution within a neighborhood. This innovative approach mitigates drastic prediction changes under small parameter updates, thus reducing forgetting. Simultaneously, it enhances new task performance by preventing overfitting. Empirical results show MACL achieves superior performance in retaining old knowledge and learning new tasks compared to existing state-of-the-art CL methods, demonstrating its effectiveness, efficiency, and versatility.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in continual learning as it introduces a novel perspective on mitigating model parameter sensitivity to improve performance. The proposed method, which seamlessly integrates with existing CL methodologies, offers significant improvements in effectiveness and versatility and opens new avenues for research in parameter sensitivity reduction and optimization of worst-case CL performance.
Visual Insights#
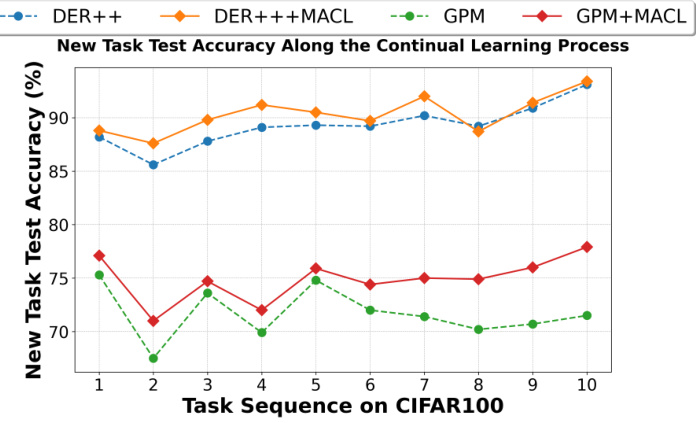
The figure shows the new task test accuracy along the continual learning process on CIFAR100. Four methods are compared: DER++, DER++ with the proposed MACL method, GPM, and GPM with MACL. The x-axis represents the task sequence (1-10), and the y-axis represents the new task test accuracy (%). The plot shows how the new task accuracy changes as new tasks are introduced during continual learning for each method. The results indicate that integrating MACL with existing methods (DER++ and GPM) significantly improves the new task performance.
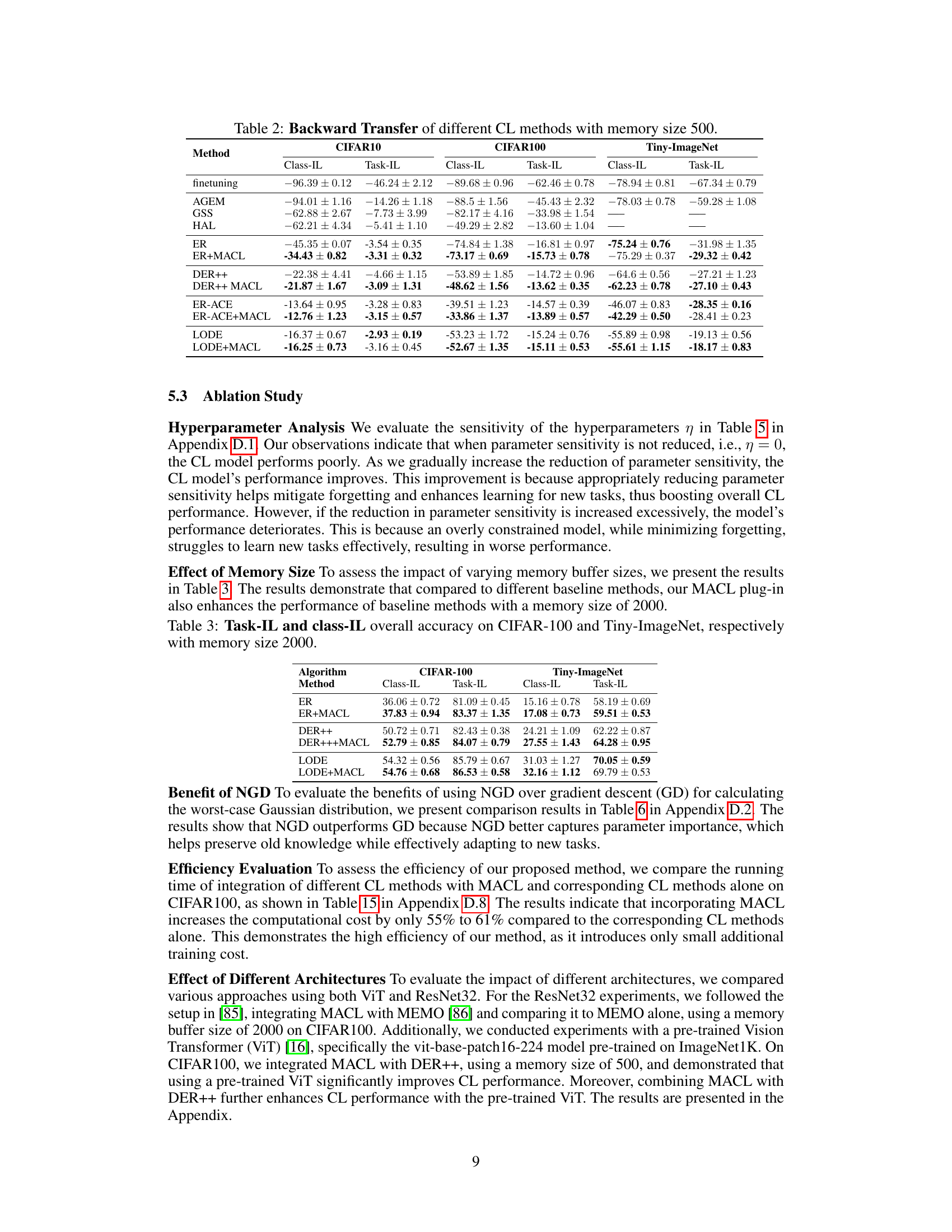
This table presents the overall accuracy results for various continual learning methods across three benchmark datasets: CIFAR-10, CIFAR-100, and Tiny-ImageNet. The results are broken down by task-incremental learning (Task-IL) and class-incremental learning (Class-IL) settings, and a memory size of 500 is used for methods that utilize memory. The ‘-’ indicates where results are not applicable or not available for a specific method and dataset combination.
In-depth insights#
CL Sensitivity#
In continual learning (CL), model sensitivity to parameter updates is a critical factor affecting performance. High sensitivity leads to catastrophic forgetting, where previously learned knowledge is lost, and overfitting to new tasks, hindering generalization. A low-sensitivity model, conversely, robustly maintains old knowledge while adapting effectively to new data distributions. Therefore, understanding and managing this sensitivity is crucial for successful CL. Strategies to mitigate sensitivity might include regularization techniques, careful parameter initialization, or optimization methods focusing on flat minima. The ideal CL model balances the ability to learn new information with the preservation of existing knowledge, demonstrating low sensitivity to parameter changes while exhibiting high performance on both old and new tasks.
NGD Optimization#
Natural Gradient Descent (NGD) optimization offers a powerful approach to continual learning by directly addressing the challenge of parameter sensitivity. Unlike standard gradient descent, NGD uses the Riemannian geometry of the parameter space to guide updates, making it particularly effective when the parameter space is highly curved, as often happens in deep learning models. By incorporating information geometry through the Fisher Information Matrix, NGD is better able to avoid catastrophic forgetting and improve generalization. However, computing the Fisher Information Matrix can be computationally expensive, which is why the paper explores efficient approximations and alternatives, such as updating parameters in the expectation space instead of the natural parameter space. This allows for faster convergence and scalability. This method ultimately aims to enhance model stability by finding the worst-case performance within a parameter distribution’s neighborhood, leading to more robust continual learning with improved performance in retaining previous knowledge while simultaneously achieving excellent results on new tasks.
Empirical Gains#
An ‘Empirical Gains’ section in a research paper would detail the practical improvements achieved by the proposed method. It would go beyond theoretical analysis to showcase real-world effectiveness. This might involve comparisons against existing state-of-the-art methods using standardized benchmarks and datasets, presenting quantitative results such as accuracy, precision, recall, F1-score, or other relevant metrics. Crucially, the section would also analyze the statistical significance of any observed improvements, ensuring that gains are not merely due to chance. A robust ‘Empirical Gains’ section should also discuss the generalizability of the results, examining performance across diverse datasets or under varied conditions to demonstrate the method’s broad applicability. Finally, it should carefully consider and acknowledge any limitations of the empirical findings, providing a balanced and nuanced perspective on the practical impact of the research.
Theoretical Bounds#
A theoretical bounds section in a machine learning research paper would rigorously analyze the performance guarantees of a proposed model. It would likely involve deriving upper and lower bounds on key metrics like generalization error or training time, often using techniques from statistical learning theory or information theory. The analysis might involve analyzing the model’s capacity, exploring relationships between model complexity and generalization performance, and potentially deriving convergence rates for the model’s learning algorithm. A strong theoretical bounds section would provide valuable insights into the model’s reliability and efficiency, complementing empirical results and offering a more complete understanding of its strengths and limitations. Furthermore, tight bounds demonstrate a more precise understanding of the model’s behavior, which enhances the paper’s contribution significantly. It may also explore the impact of hyperparameters and dataset characteristics on those bounds, providing practical guidelines for model deployment. Well-defined assumptions underpinning the theoretical analysis are critical for ensuring the validity and interpretability of the derived bounds.
Future Works#
Future work could explore extending the model’s applicability to more complex continual learning scenarios, such as those involving concept drift or significant changes in data distribution. Investigating the impact of different forgetting mitigation techniques when integrated with the proposed method would be valuable. A thorough analysis of the method’s scalability and computational cost, particularly for very large datasets or complex models, is necessary. Additionally, applying the framework to different modalities and tasks beyond image classification could reveal its generalizability and robustness. Furthermore, a deeper investigation into the theoretical underpinnings of the model’s parameter sensitivity is needed to establish a stronger theoretical foundation and potentially enhance its performance. Finally, exploring how to make the framework more user-friendly and easily integrated with existing CL methodologies would facilitate its wider adoption and deployment in real-world applications.
More visual insights#
More on tables
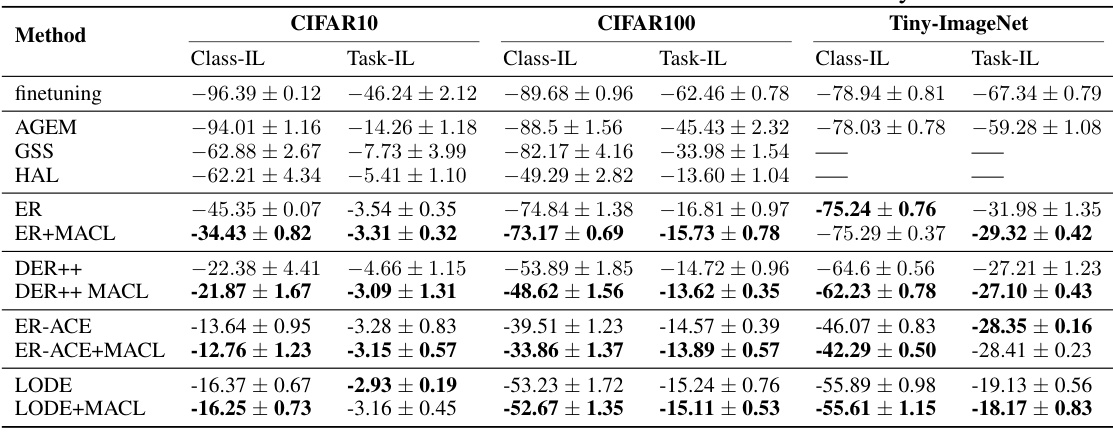
This table presents the overall accuracy results for task-incremental learning (Task-IL) and class-incremental learning (Class-IL) on three benchmark datasets: CIFAR-10, CIFAR-100, and Tiny-ImageNet. The results are reported for various continual learning methods (including the proposed MACL method and several baselines) and compare their performance under different learning scenarios. A memory size of 500 is used across all experiments.
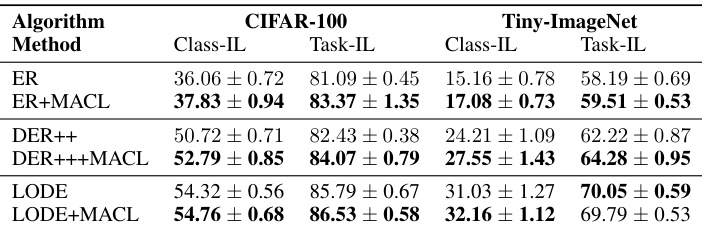
This table presents the results of Task-IL and Class-IL experiments conducted on CIFAR-100 and Tiny-ImageNet datasets using a memory size of 2000. It compares the performance of different continual learning methods (ER, ER+MACL, DER++, DER+++MACL, LODE, and LODE+MACL) in terms of overall accuracy. The results show the impact of integrating the proposed MACL method with existing continual learning approaches.

This table shows the overall accuracy results of integrating DER++ with MACL on the Tiny-ImageNet dataset. The experiment was conducted using a memory buffer size of 500, and the number of tasks in the continual learning sequence was varied (10 and 20 tasks). The results demonstrate the performance improvement achieved by integrating MACL with DER++, even with longer task sequences, highlighting the effectiveness of the method in improving overall accuracy across multiple tasks.

This table presents the results of an ablation study on the hyperparameter η, which controls the sensitivity of the model to parameter updates. The study evaluates the effect of different values of η on the overall accuracy of the model on two datasets, CIFAR100 and Tiny-ImageNet, when performing task-incremental learning (Task-IL). The results show how the model’s performance changes as the sensitivity to parameter updates is adjusted.

This table compares the performance of the proposed method MACL using two different optimization methods: Natural Gradient Descent (NGD) and Gradient Descent (GD). The results show the overall accuracy achieved on two benchmark datasets, CIFAR100 and Tiny-ImageNet, under the task-incremental learning setting. This demonstrates the impact of the optimization method on the model’s ability to retain knowledge and achieve good performance on new tasks. The values show the improvement of using NGD compared to GD for MACL.

This table presents the results of online continual learning experiments on the CIFAR100 dataset under blurry boundary conditions. It compares the performance of the MKD(PCR) method alone with the performance of MKD(PCR) enhanced by the proposed MACL method. The comparison is made across varying memory sizes (1000, 2000, and 5000). The results demonstrate the improvement in accuracy achieved by integrating MACL into the baseline MKD(PCR) method.

This table presents the results of online continual learning experiments on the Tiny-ImageNet dataset under blurry boundary conditions. It compares the performance of the MKD(PCR) method with and without the proposed MACL approach, across three different memory sizes (2000, 5000, and 10000). The results show the improvement achieved by integrating MACL into the MKD(PCR) method for enhancing online continual learning performance under challenging conditions.

This table shows the overall accuracy results of integrating the proposed MACL method with the DER++ baseline method on the Tiny-ImageNet dataset. The experiment is performed using a memory buffer size of 500 and varies the number of tasks in the sequence to assess the impact of longer task sequences. The results are reported separately for both Class-IL and Task-IL scenarios. The table highlights that even with longer sequences of tasks, the MACL method improves performance compared to the baseline DER++ method.

This table presents a comparison of the performance of various continual learning methods (ER, ER+MACL, DER++, and DER++MACL) on the 5-datasets benchmark, which consists of five distinct datasets (CIFAR-10, MNIST, Fashion-MNIST, SVHN, and notMNIST). The results are shown for both Class-IL (class-incremental learning) and Task-IL (task-incremental learning) settings. The table showcases the accuracy achieved by each method, illustrating the effectiveness of MACL when integrated with other continual learning techniques.

This table presents the overall accuracy achieved using the MEMO algorithm alone and when combined with the proposed MACL method. The experiment uses ResNet32 as the base model and a memory buffer of 2000. The results showcase the improvement in accuracy obtained by integrating MACL with MEMO.

This table presents the overall accuracy results for Class-IL and Task-IL scenarios on the CIFAR100 dataset using a Vision Transformer (ViT) model. The results compare the performance of the DER++ method alone against the performance of DER++ integrated with the proposed MACL method. The memory buffer size is set to 500. The table shows that incorporating MACL into DER++ improves the overall accuracy for both Class-IL and Task-IL settings.

This table presents the results of the ImageNet-R experiments. It shows the performance (Class-IL and Task-IL accuracy) of four different continual learning methods: DER++, DER++ with the proposed MACL method, LODE, and LODE with MACL. The memory size used was 500. The results demonstrate the improvement in accuracy achieved by integrating the MACL method with existing state-of-the-art continual learning approaches.

This table presents the results of the CUB200 dataset experiment. It shows the overall accuracy for class-incremental learning (Class-IL) and task-incremental learning (Task-IL) using different continual learning methods. The methods compared include DER++, DER++ with the proposed MACL method, LODE, and LODE with MACL. The table highlights the performance gains achieved by integrating the MACL method with existing continual learning techniques.
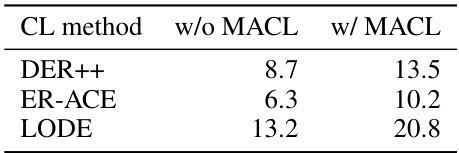
This table shows the running time (in seconds) for training a single epoch on the CIFAR100 dataset for several continual learning (CL) methods, both with and without the integration of the proposed Model Sensitivity Aware Continual Learning (MACL) method. The table compares the efficiency gains obtained by incorporating MACL into existing CL techniques.

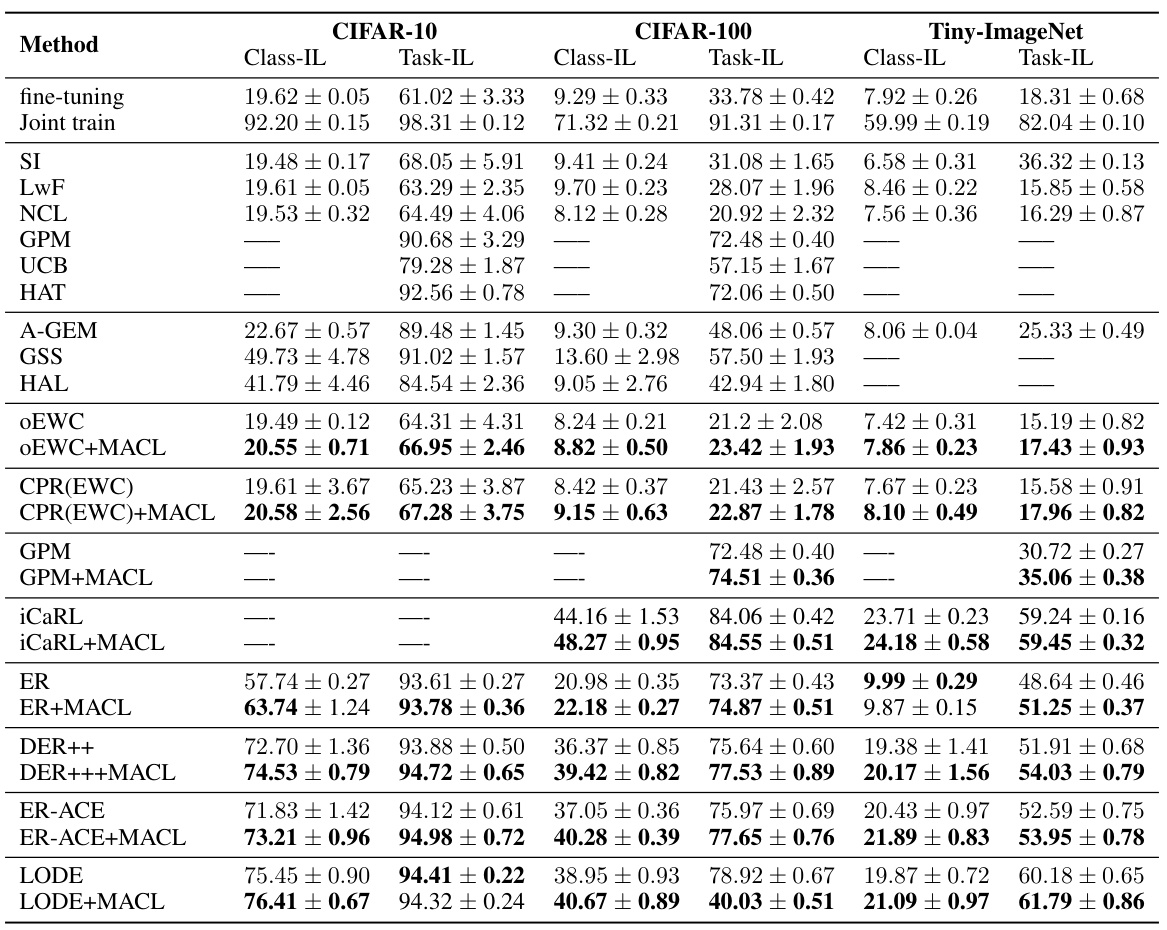
This table presents the overall accuracy results for Task-IL and Class-IL experiments conducted on three datasets: CIFAR10, CIFAR100, and Tiny-ImageNet. The results are categorized by method and include a comparison with fine-tuning and joint training baselines. The memory size used for the experiments was 500. A ‘-’ symbol denotes that the result is not applicable or available for that particular method and dataset combination.
Full paper#