Optimizing the coalition gain in Online Auctions with Greedy Structured Bandits

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in online advertising and multi-armed bandits. It introduces novel algorithms with problem-dependent and problem-independent regret bounds, offering practical solutions for maximizing coalition gain in online auctions while respecting privacy constraints. The work opens avenues for further research in structured bandits and privacy-preserving mechanisms within the online advertising domain.

Visual Insights

#

This figure empirically validates the theoretical regret bounds presented in Table 1. It shows the cumulative regret R(T) over time T for different multi-armed bandit algorithms: Local Greedy (LG), Greedy Grid (GG), Upper Confidence Bound 1 (UCB1), Exponential-weight algorithm for exploration and exploitation (EXP3), and Optimistic Upper Confidence Bound for Unimodal bandits (OSUB). The experiment uses a Bernoulli distribution with parameter 0.05 to generate bidder values, a coalition size of N=100, and p=4 competitors. The plot displays the average regret over 20 independent simulations, with error bars showing the first and last deciles, illustrating the variability of the results.

This table compares the upper bounds on the regret for various multi-armed bandit algorithms. The algorithms include EXP3, UCB1, OSUB, and the novel Local-Greedy (LG) and Greedy-Grid (GG) algorithms proposed in this paper. The regret upper bounds are expressed using Big O notation, highlighting the dependence on parameters such as the number of arms (N), the time horizon (T), and various gap parameters (Δ, ∆n, ∆n*+1, ∆n*-1) representing the differences in reward between arms. The table shows that the proposed LG and GG algorithms achieve problem-dependent regret, in contrast to EXP3 and UCB1, while GG also provides problem-independent guarantees.

In-depth insights

#

Greedy Bandit Alg

#

A greedy bandit algorithm is a reinforcement learning approach that balances exploration and exploitation by making decisions that are locally optimal at each step. This approach prioritizes immediate reward, making it efficient but potentially suboptimal in the long run. The core idea is to select the action with the highest estimated reward based on the current knowledge, ignoring the potential future gains from exploring less-known actions. The effectiveness of such algorithms strongly depends on the environment’s structure, especially the reward function’s shape and the presence of any hidden states or non-stationarity. In simpler settings, greedy algorithms can be remarkably effective, offering fast convergence and computational ease. However, in complex scenarios with uncertainty or delayed rewards, they might fail to identify the true optimal policy because of myopic decision-making. Therefore, the choice between a greedy approach and more sophisticated algorithms like UCB or Thompson Sampling depends on the complexity of the problem and the balance needed between computational efficiency and solution optimality. Often, hybrid approaches combining greedy exploration with more cautious strategies are favored to maximize both speed and performance.

Coalition Gain

#

The concept of “Coalition Gain” in the context of online auctions centers on optimizing the collective reward a group of agents (a coalition) achieves by participating in an auction. Individual agents have private valuations for the item, and the coalition’s decision-maker faces the challenge of selecting a subset of agents to maximize their collective profit, considering the trade-off between increased bidding power (higher chance of winning) and higher costs. The paper likely explores various strategies, such as greedy algorithms, to determine the optimal number of coalition members to deploy for each auction, given limited information and the dynamic nature of online environments. The key challenge is balancing exploration (learning about the reward function) and exploitation (maximizing immediate profit), which is further complicated by privacy constraints that restrict the availability of information. A crucial aspect will be the development and analysis of algorithms that can efficiently learn the optimal coalition size while adhering to privacy restrictions. The core problem is framed as a structured bandit problem, allowing for sophisticated algorithmic approaches and theoretical regret analysis, especially considering the unimodality property of the reward function under certain assumptions.

Reward Estimation

#

The reward estimation process is crucial for the effectiveness of the proposed algorithms. The paper cleverly leverages the knowledge that the expected reward function, r(n), is fully determined by the underlying cumulative distribution function (CDF), F, and the number of bidders. This allows for the estimation of r(n) using samples collected from any arm k ∈ [N], rather than just arm n itself. This innovative approach simplifies the problem while maintaining accuracy. The paper provides theoretical guarantees on the accuracy of these estimations using novel concentration bounds, demonstrating that the estimates’ reliability strongly depends on the relationship between the selected arm (k) and the target arm (n). Concentration bounds are derived using a novel approach which considers the relative position of k with respect to n, further enhancing the efficiency of the reward estimation. This innovative estimation technique serves as the foundation for the proposed bandit algorithms, allowing them to efficiently learn and optimize the coalition’s gain in repeated second-price auctions.

Regret Guarantees

#

Regret, in the context of online learning algorithms like those used in this paper, quantifies the difference between the cumulative reward achieved by an algorithm and that achieved by an optimal strategy. Strong regret guarantees are crucial, demonstrating an algorithm’s efficiency. This paper focuses on structured bandits, leading to problem-dependent regret bounds. Problem-dependent bounds mean the regret’s scaling depends on characteristics of the problem itself, such as the gaps between rewards of different arms (actions). The analysis provides upper bounds on regret for two algorithms (LG and GG), demonstrating both achieve constant regret independent of the time horizon (T). However, LG’s regret depends on the minimum gap between adjacent arms’ rewards, while GG’s depends on the gap between the optimal arm and other arms. The paper also details the derivation of confidence bounds on reward estimates, a key component in proving the regret guarantees. These bounds account for the uncertainty introduced by limited observations in online auctions, thus impacting the algorithms’ performance.

Future Works

#

The paper’s “Future Works” section could explore several promising avenues. Extending the algorithms to handle multiple auctions simultaneously would be highly impactful for real-world DSP applications. This would involve addressing the complexities of coordinating campaign participation across various auctions, potentially using novel optimization techniques. Furthermore, relaxing the identical bidders assumption and incorporating bidder heterogeneity would significantly increase the model’s realism. Investigating the effect of different bidding strategies on the algorithm’s performance is also important, particularly in the context of privacy-preserving mechanisms. Finally, a thorough theoretical analysis of the algorithms’ performance under non-unimodal reward functions is essential, aiming to provide tighter regret bounds or develop alternative algorithms that are robust to this assumption’s violation. Empirical validation of these extensions through extensive simulations using real-world data would be crucial to confirm the practical benefits of these enhancements.

More visual insights

#

More on figures

This figure shows the shape of the expected reward function r(n) for different parameters of the Beta distribution and the number of competing bidders (p). The x-axis represents the number of bidders from the coalition (n), and the y-axis represents the expected reward r(n). The different colored lines represent different Beta distributions and values for p. The figure illustrates the unimodal nature of r(n) for the Beta distribution, which is a key assumption in the paper’s theoretical analysis.

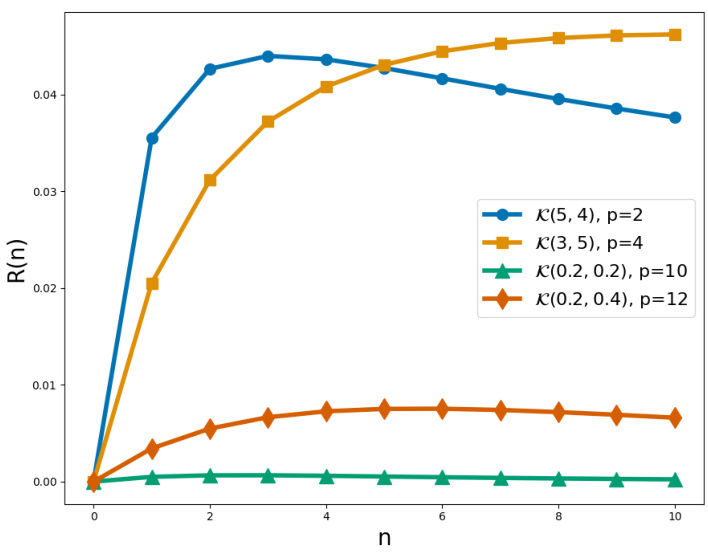
This figure shows the shape of the expected reward function r(n) for different parameters of the Kumaraswamy distribution and p. The Kumaraswamy distribution is defined by F(x) = 1 − (1 − x^a)^b for some parameters (a, b). The plot illustrates the unimodal shape of r(n) for different parameter settings, showcasing how the reward function changes with varying values of ’n’ (number of bidders from the coalition) and ‘p’ (number of competing bidders).

This figure empirically validates the theoretical regret bounds from Table 1. It shows the expected regret R(T) over time horizon T for several multi-armed bandit algorithms: UCB1, Exp3, OSUB, Local Greedy (LG), and Greedy Grid (GG). The simulation parameters are a Bernoulli distribution with parameter 0.05, coalition size N=100, and competitor size p=4. The shaded region represents the first and last deciles across 20 simulations, indicating variability.

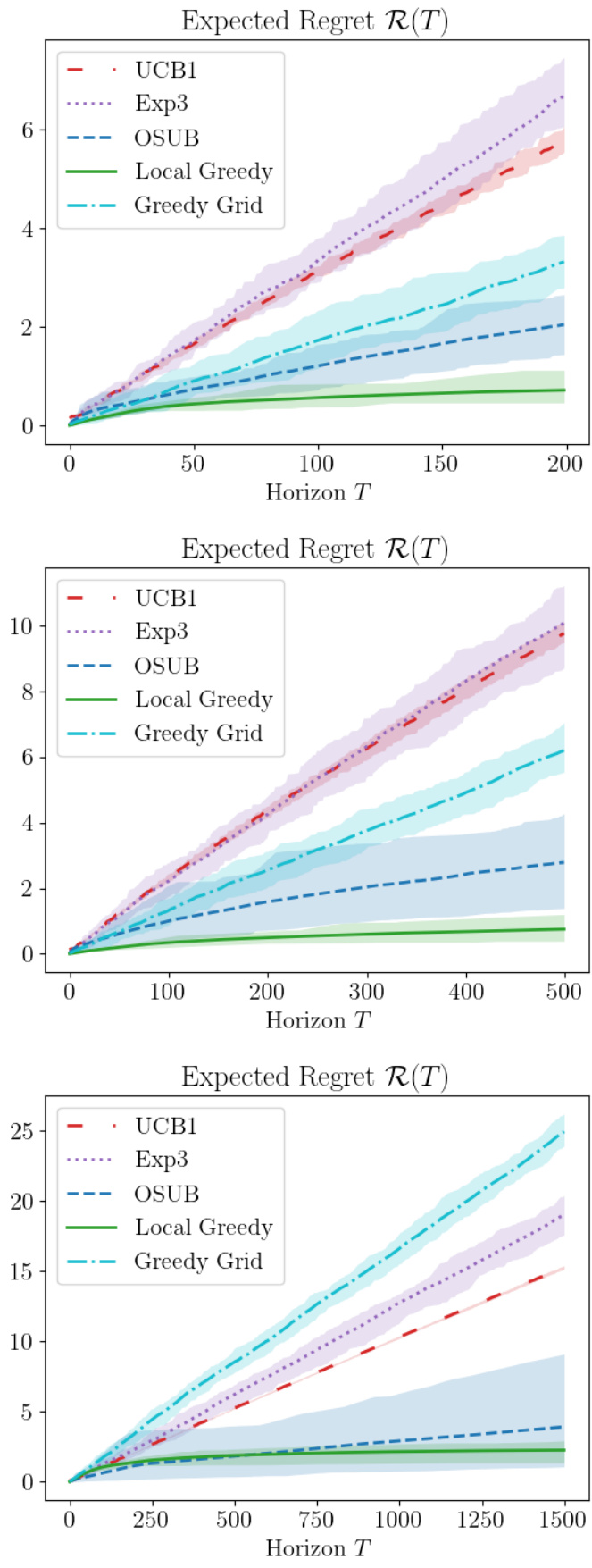
This figure shows the results of three different experimental settings with different parameters for the number of players, the number of competitors, and the distribution of player values. The purpose is to illustrate the practical performance of the Local Greedy algorithm across various scenarios. The figure compares the performance of Local Greedy to UCB1, Exp3, OSUB, and Greedy Grid algorithms, demonstrating that Local Greedy consistently outperforms these baselines, achieving a constant regret regime in each setting much faster than other methods. Table 2 provides the specific parameter values used in each of these three experimental settings.

More on tables

This table compares the regret upper bounds for various multi-armed bandit algorithms. It shows the theoretical guarantees on the cumulative regret (R(T)) achieved by different algorithms, highlighting their dependencies on the number of arms (N), the time horizon (T), and problem-specific parameters such as the gaps between rewards of different arms (∆n, ∆). The algorithms compared include EXP3, UCB1, OSUB, and the two novel algorithms proposed in the paper: LG (Local Greedy) and GG (Greedy Grid). The table provides a concise summary of the theoretical performance differences.

This table compares the upper bounds on regret for different multi-armed bandit algorithms. The algorithms include EXP3, UCB1, OSUB, and the two novel algorithms presented in the paper, LG (Local Greedy) and GG (Greedy Grid). The regret bounds are expressed in Big O notation and show the dependence on various parameters like the number of arms (N), the time horizon (T), and problem-dependent gaps (Δ). LG and GG achieve problem-dependent regret, which means their regret is constant regardless of the time horizon T.

This table compares the upper bounds on regret for different multi-armed bandit algorithms. The algorithms include EXP3, UCB1, OSUB, Local-Greedy (LG), and Greedy-Grid (GG). The regret upper bounds are expressed using Big O notation and show the dependence on various factors such as the number of auctions (T) and the number of arms (N), with problem-dependent and problem-independent guarantees shown for LG and GG.

Full paper

#