MatrixNet: Learning over symmetry groups using learned group representations

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working with symmetry groups, particularly in machine learning and mathematics. It introduces a novel method for handling groups, which can be directly applied to many open problems. The improved sample efficiency and generalization shown will impact numerous applications, and the efficient matrix representation offers a new direction for parameter-efficient model design.

Visual Insights

#

This figure shows a schematic of the MatrixNet architecture for predicting the order of elements in the symmetric group S3. The input consists of a sequence of generators (σ1, σ2, etc.), representing a group element. Each generator is passed through a ‘Matrix Block,’ which learns a matrix representation of that generator. These matrix representations are sequentially multiplied to obtain a matrix representation of the input group element. Finally, this matrix representation is flattened and fed into a task model (a Multilayer Perceptron or MLP in this case) to predict the order of the group element.

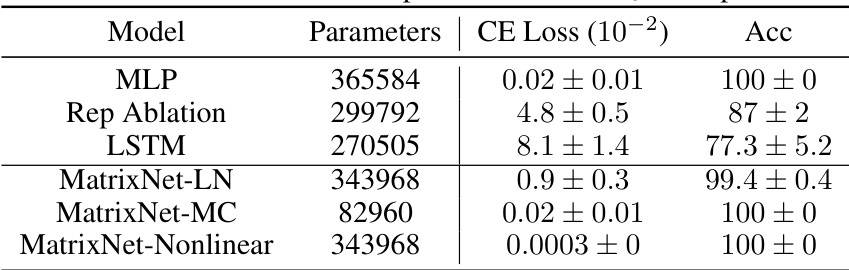
This table presents a comparison of the performance of MatrixNet variants and three baseline models (MLP, LSTM, and a model with a fixed representation) on an order prediction task for the symmetric group S10. The table shows the number of parameters, cross-entropy loss, and accuracy for each model. The results demonstrate that MatrixNet achieves superior performance, particularly MatrixNet-Nonlinear and MatrixNet-MC, with near-perfect accuracy and significantly lower loss compared to the baselines.

In-depth insights

#

Learned Group Reps

#

The concept of “Learned Group Representations” presents a significant advancement in applying group theory to machine learning. Instead of relying on predefined, fixed representations, this approach dynamically learns matrix representations of group elements. This offers several key advantages: enhanced sample efficiency due to the model’s adaptability to specific tasks, improved generalization through the incorporation of inherent algebraic structure, and increased parameter efficiency by focusing on learning representations of generators only. The method’s ability to generalize to unseen group elements, even those with longer word lengths than seen during training, highlights its potential for handling complex, large-scale groups. The learned representations themselves offer potential for interpretability, allowing investigation into the model’s understanding of the underlying group structure and its implications for the specific task at hand. The success of this technique, especially demonstrated in the experiments using symmetric groups and Artin braid groups, shows the power of learning to leverage the structure of groups for better machine learning performance.

MatrixNet Design

#

MatrixNet’s design centers on learning group representations, a departure from using predefined ones. This is achieved through matrix blocks, which map group generators to invertible matrices. The core innovation lies in learning these mappings, allowing the model to adapt to specific tasks and implicitly capture relevant algebraic structure. Sequential matrix multiplication combines individual matrix representations to form representations of composite group elements. This architecture respects group axioms and relations via a novel combination of model design (e.g., enforcing invertibility of matrix representations) and a regularization loss function that penalizes deviations from group relations. This approach leads to improved sample efficiency and generalization compared to baselines, particularly when dealing with unseen group elements, demonstrating MatrixNet’s capacity for leveraging group structure effectively in machine learning tasks.

Braid Group Action

#

The concept of a braid group action is central to the paper’s exploration of learning over symmetry groups. The braid group, unlike many finite groups, is infinite and its representations are not fully classified. This poses a significant challenge for applying standard machine learning techniques that rely on fixed, pre-defined group representations. The authors cleverly address this by introducing MatrixNet, an architecture that learns matrix representations of group elements, rather than relying on pre-defined ones. This allows MatrixNet to effectively handle the complexities of the braid group’s structure and to generalize to unseen group elements. The task of estimating the sizes of categorical objects under a braid group action is presented as a crucial test case showcasing MatrixNet’s capacity for handling complex group operations and generalizing beyond the training data. The success of MatrixNet in this context highlights the power of learning group representations directly from data, particularly when dealing with groups that lack a well-understood representation theory. The paper’s experimental results, therefore, suggest that learned representations offer a more adaptable and efficient approach for handling complex algebraic structures, opening avenues for future research in applying machine learning to problems within abstract algebra and topology.

Extrapolation Limits

#

The concept of “Extrapolation Limits” in the context of a machine learning model trained on a symmetry group, like the braid group, refers to how well the model generalizes to inputs (braid words) of lengths unseen during training. A successful model should exhibit robustness, maintaining accuracy even with significantly longer braid words. However, limitations are expected, as the model’s learned representations might not perfectly capture the group’s complex structure. Failure to extrapolate effectively could indicate either insufficient training data, a flawed model architecture unable to capture long-range dependencies within the braid group, or the inherent difficulty in representing the group’s infinite nature in a finite model. Analyzing extrapolation limits requires careful evaluation of model performance on unseen word lengths, examining error metrics to pinpoint the type of failure (e.g., gradual degradation or sudden collapse), and perhaps further investigation into the learned representations to uncover potential weaknesses in the model’s understanding of the underlying group structure. The presence or absence of extrapolation capabilities is a key benchmark for assessing a model’s true understanding of the symmetry group. Therefore, the study of extrapolation limits can offer valuable insights into model limitations and guide future improvements in the design of group-theoretic machine learning models.

Future Directions

#

The research paper’s ‘Future Directions’ section would ideally explore extending the MatrixNet architecture to handle continuous groups (Lie groups), a significant leap from the current discrete group focus. This would involve adapting the learned matrix representations to account for the continuous nature of Lie group elements and their operations, potentially using techniques from differential geometry. Another key area for future work involves improving the scalability of MatrixNet. While the paper demonstrates success on relatively small groups, the extension to larger groups or infinite groups (like braid groups) poses computational challenges. Investigating alternative data structures or more efficient learning techniques is critical for addressing this. A deep dive into the interpretability of the learned matrix representations is crucial. The paper hints at connections to irreducible representations, but a comprehensive exploration of this could lead to valuable insights into how the network learns group structure and its relationship to the task. Finally, the application of MatrixNet to a wider range of mathematical problems beyond those in the paper needs to be explored. The use of MatrixNet in other areas of mathematics, including knot theory, topology, and theoretical physics, presents exciting possibilities. Further investigation could reveal surprising connections and lead to novel theoretical advancements.

More visual insights

#

More on figures

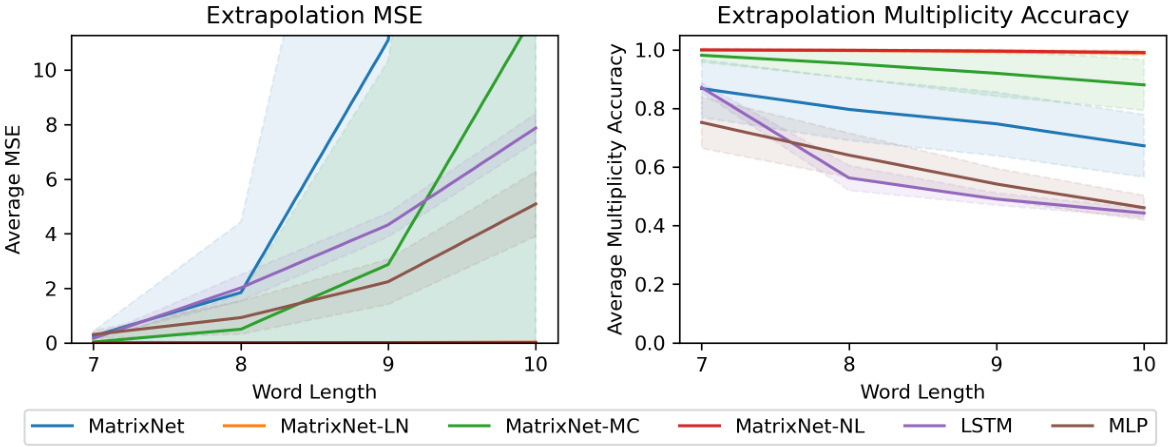
This figure displays the results of a length extrapolation experiment. The left panel shows the Mean Squared Error (MSE) for different models as the length of the input sequence increases. It shows that MatrixNet and MatrixNet-MC have a significant increase in MSE with longer sequences, while MatrixNet-LN and MatrixNet-NL show much more stable performance, even approaching zero MSE. The right panel shows that despite the increased MSE, MatrixNet and MatrixNet-MC maintain relatively high accuracy compared to baselines which suggests their high MSE may be due to outliers in prediction. Overall, this illustrates the generalization abilities of different model variants.

This figure visualizes the learned matrix representations of the braid group B3. The leftmost two heatmaps represent the learned representations for the generators g1 and g2. The rightmost two heatmaps show the representations for two longer braid words, g1g1g2g1g2 and g2g2g1g2g2, which are equivalent due to the group relations. The similarity in the heatmaps for these equivalent words demonstrates the model’s ability to learn representations that respect the group structure.

This figure illustrates the architecture of MatrixNet, a neural network designed for learning functions on a group. The input is a sequence of group generators (σ1, σ2 in this example, representing elements of the symmetric group S3). Each generator is mapped to a learned matrix representation (through a ‘Matrix Block’), and these matrices are sequentially multiplied. The resulting matrix represents the input group element. Finally, this matrix representation is processed by a Multilayer Perceptron (MLP) task model to predict the output (in this case, the order of the group element).

More on tables

This table presents the results of applying MatrixNet to order prediction tasks on various finite groups. It shows the group used (including its order |G|), the size of the learned matrix representation used, the number of classes in the prediction task (which varies based on the possible orders in the group), the cross-entropy loss (CE Loss), and the accuracy (Acc). The results demonstrate MatrixNet’s ability to generalize across different group structures and sizes.

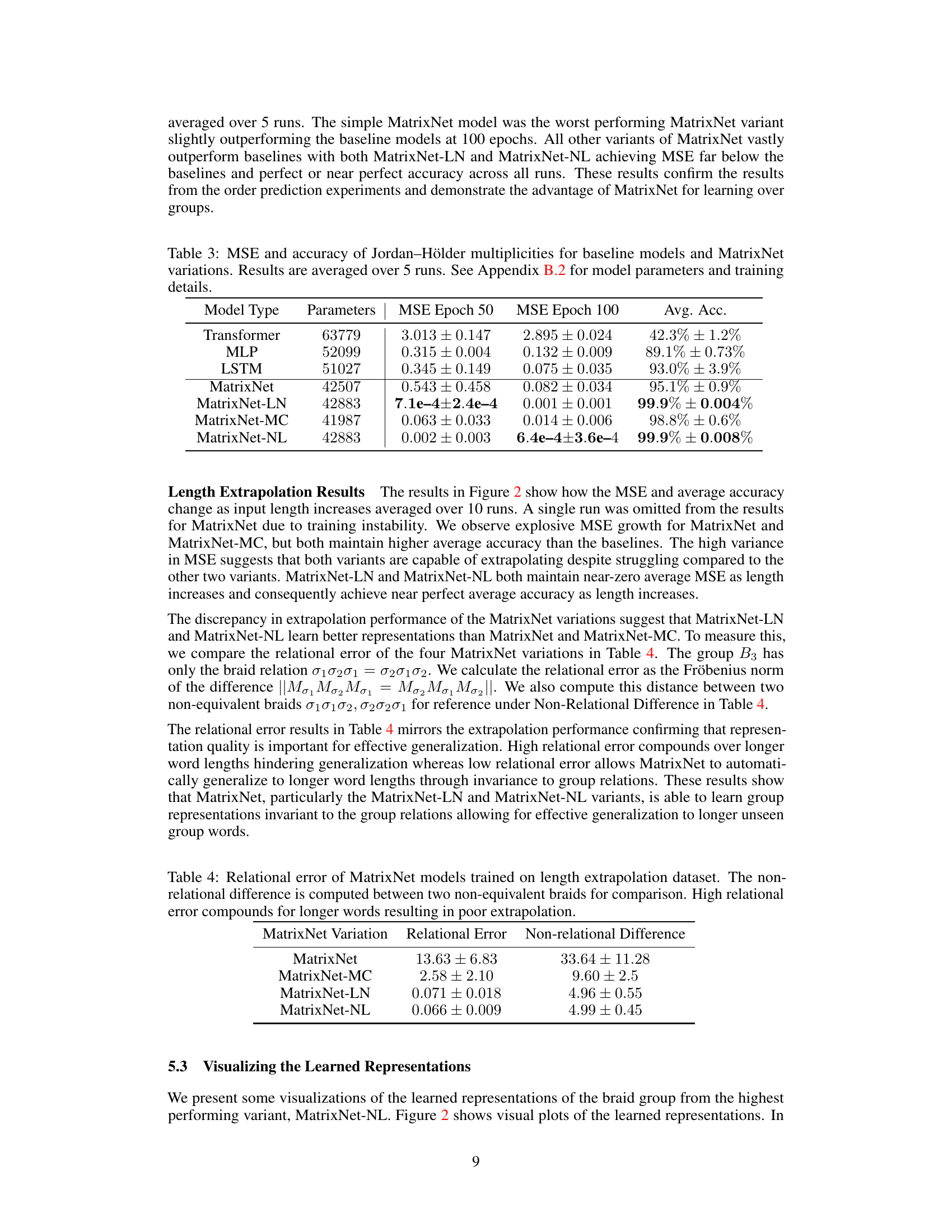
This table presents the Mean Squared Error (MSE) and average accuracy of different models in predicting the Jordan–Hölder multiplicities. The models compared include several baseline models (Transformer, MLP, LSTM) and various MatrixNet architectures (MatrixNet, MatrixNet-LN, MatrixNet-MC, MatrixNet-NL). The MSE is reported for both epoch 50 and epoch 100, providing a measure of model performance over training time. Average accuracy represents the overall correctness of the multiplicity predictions. Appendix B.2 provides further details on model parameters and training settings.

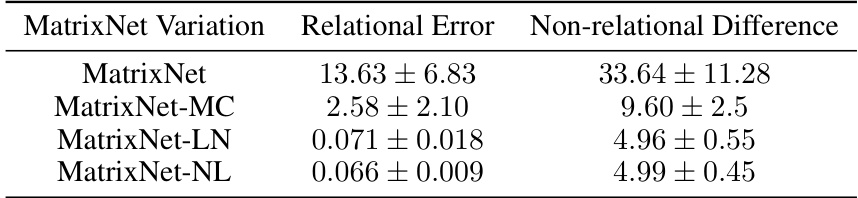
This table presents the relational error and non-relational difference for four variations of the MatrixNet model. The relational error measures how well the learned matrix representations respect the group relations of the braid group B3, while the non-relational difference is a comparison between two non-equivalent braids. Lower relational error indicates better generalization to longer, unseen braid words. The results suggest that MatrixNet-LN and MatrixNet-NL are superior in their ability to generalize.

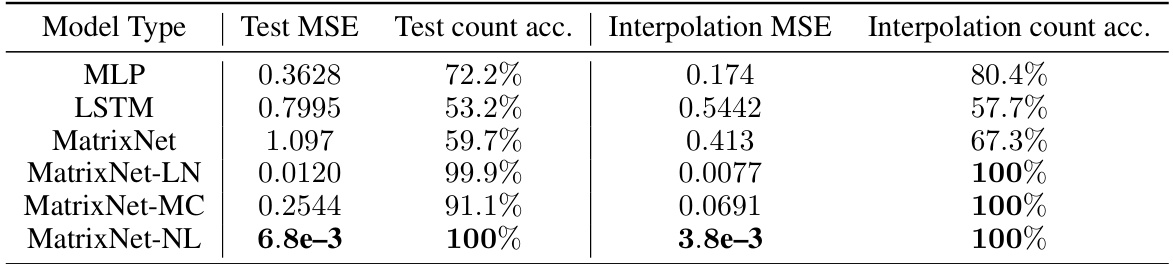
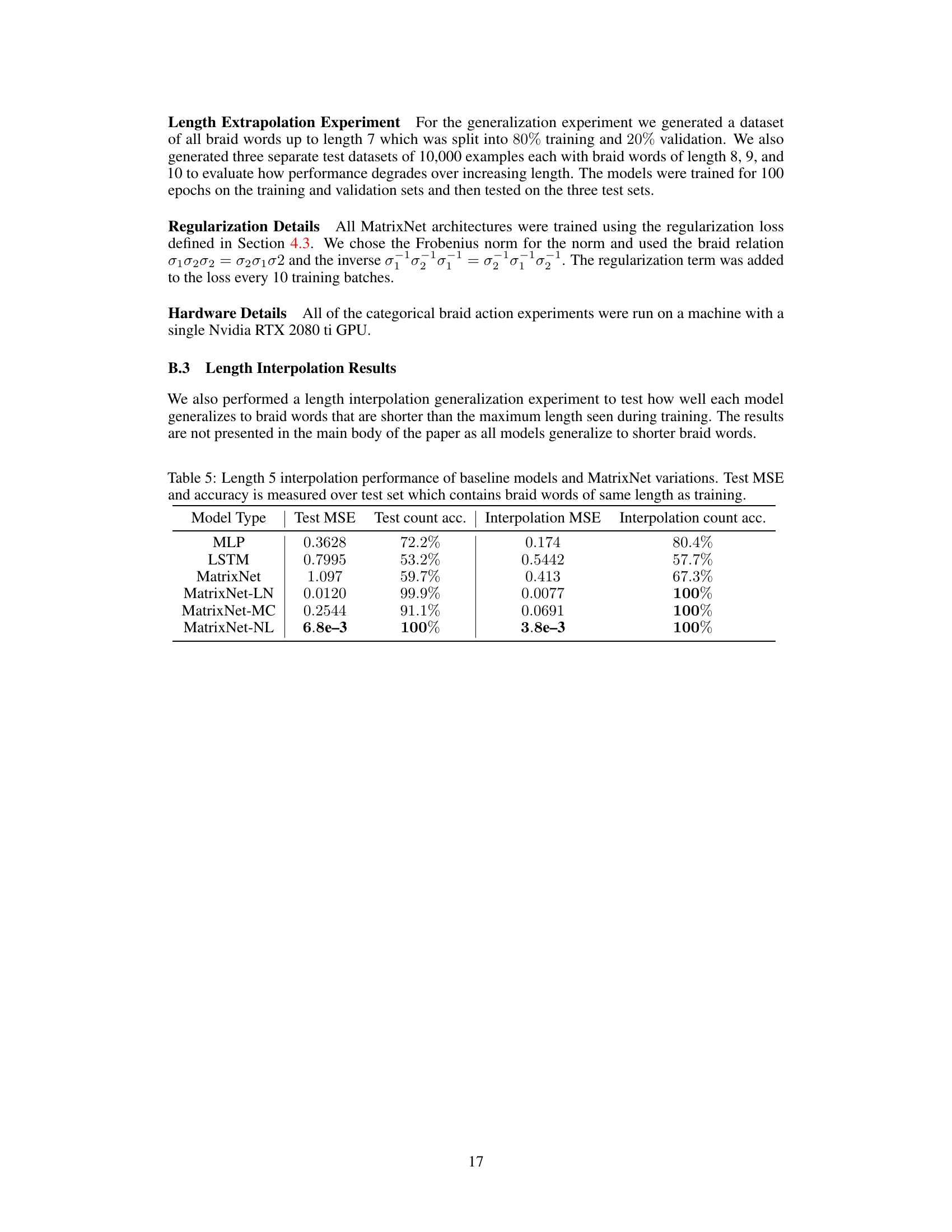
This table presents the Mean Squared Error (MSE) and accuracy results for models trained on braid words of length 5, evaluated on test sets containing braid words of length 5. It compares the performance of several baseline models (MLP, LSTM) against various MatrixNet architectures (MatrixNet, MatrixNet-LN, MatrixNet-MC, MatrixNet-NL). The results demonstrate the superior performance of MatrixNet variations, particularly MatrixNet-LN and MatrixNet-NL, which achieve near-perfect accuracy.

Full paper

#