↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Out-of-distribution (OOD) detection is crucial for reliable AI systems. However, current top-performing methods achieve high sensitivity by sacrificing robustness, meaning they fail when encountering even minor noise. This severely limits their practical use. This “sensitive-robust” dilemma arises from conflicting learning objectives: OOD detection prioritizes high uncertainty for unseen data, while generalization demands robust and confident predictions even with distributional shifts.
To address this, the researchers introduce a novel Decoupled Uncertainty Learning (DUL) method. DUL elegantly decouples the uncertainty learning objectives, allowing the model to separately handle semantic and covariate shifts. This results in significantly improved OOD detection and generalization, without the trade-off seen in previous methods. The paper provides both a theoretical analysis and empirical evidence supporting the effectiveness of DUL. The dual-optimal performance without sacrificing robustness is a significant advancement in building trustworthy AI.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses a critical limitation in existing out-of-distribution (OOD) detection methods. Many state-of-the-art OOD detectors prioritize sensitivity over robustness, leading to poor generalization in real-world scenarios with noisy data. This work provides a theoretical understanding of this “sensitive-robust” dilemma and proposes a novel solution, DUL, achieving a dual-optimal performance without sacrificing generalization ability. This opens new avenues for more reliable and trustworthy AI systems.
Visual Insights#

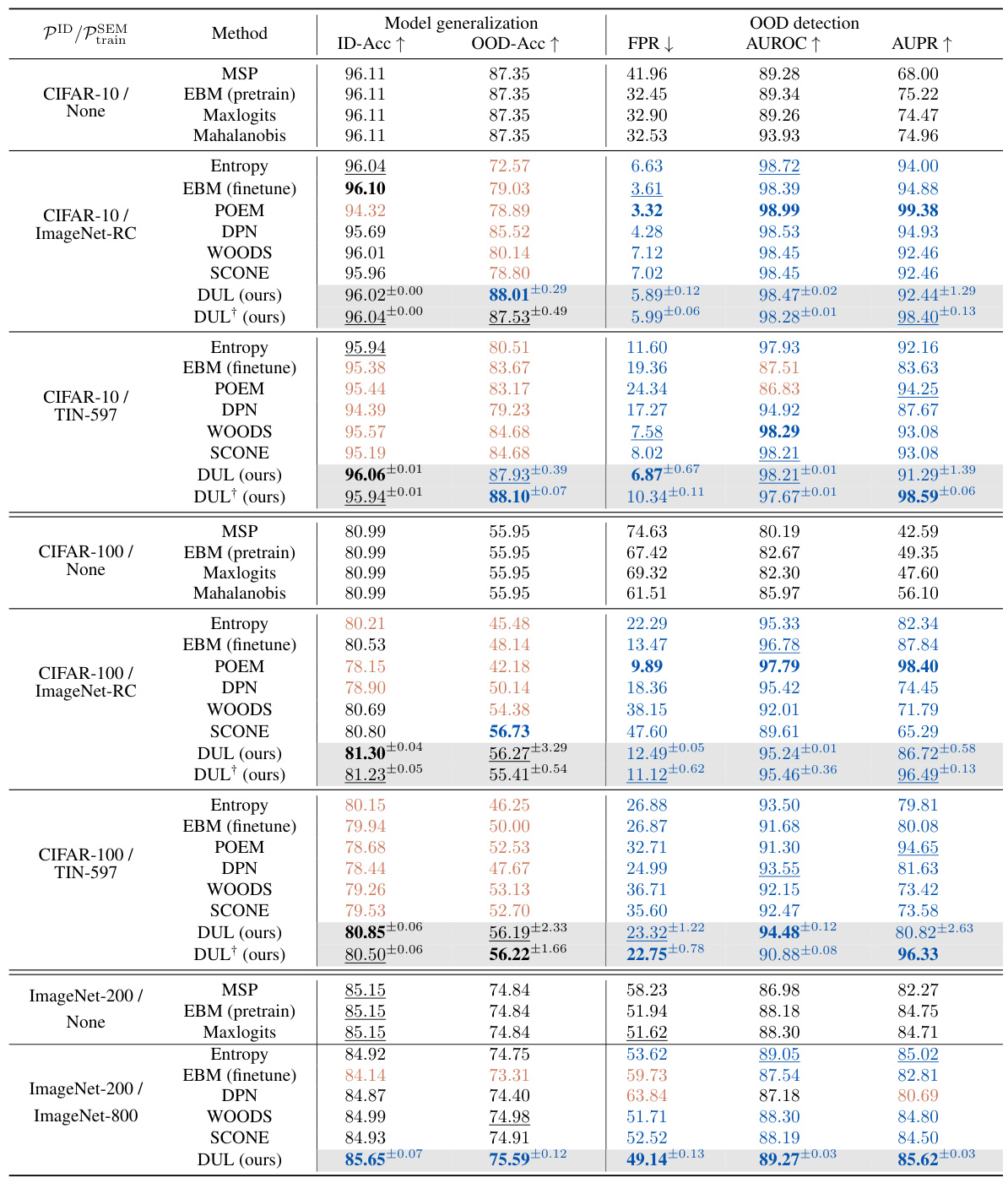
This figure demonstrates the challenges of out-of-distribution (OOD) detection and generalization in real-world scenarios. (a) shows three types of data an autonomous driving model might encounter: in-distribution (ID) data, covariate-shifted OOD data (e.g., a car in rainy conditions), and semantic OOD data (e.g., a deer on the road). (b) illustrates the dilemma faced by state-of-the-art (SOTA) OOD detection methods, which achieve superior OOD detection performance by sacrificing OOD generalization ability, creating a trade-off.
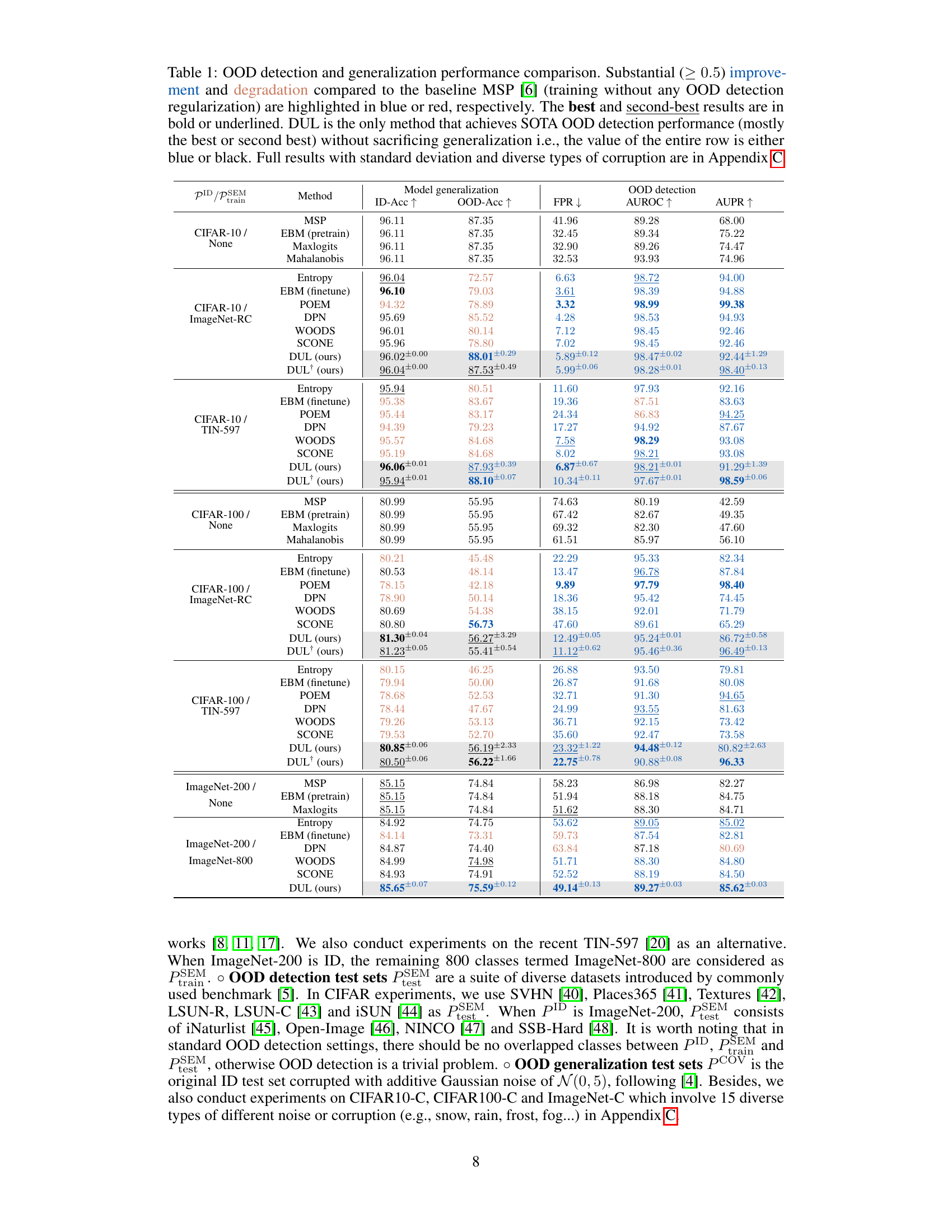
This table compares the performance of various OOD detection methods, including the proposed DUL, across multiple datasets and metrics. It highlights the trade-off between OOD detection and generalization ability observed in existing methods and shows that DUL achieves state-of-the-art OOD detection without sacrificing generalization performance. The table provides ID accuracy, OOD accuracy, false positive rate at 95% true positive rate (FPR95), AUROC, and AUPR for each method and dataset. Significant improvements and degradations compared to a baseline method (MSP) are highlighted.
In-depth insights#
OOD Dilemma#
The “OOD Dilemma” highlights the inherent conflict in machine learning models between achieving high out-of-distribution (OOD) detection accuracy and maintaining robust generalization performance. State-of-the-art OOD detection methods often prioritize sensitivity to outliers, sometimes at the expense of accuracy when encountering noisy or slightly shifted in-distribution data. This is a critical limitation because reliable generalization is crucial for trustworthy real-world applications. The dilemma arises from the often conflicting learning objectives: OOD detection pushes for high uncertainty scores on unseen data, while good generalization requires confident and consistent predictions even under distributional shifts. Successfully resolving this requires a principled approach that decouples these objectives, enabling a model to simultaneously detect outliers sensitively and generalize robustly. This represents a crucial challenge that demands further research into more sophisticated uncertainty estimation techniques and novel training strategies that address the inherent trade-off without sacrificing either detection accuracy or generalization capabilities.
DUL Framework#
The Decoupled Uncertainty Learning (DUL) framework offers a novel approach to OOD detection by decoupling uncertainty learning. Instead of relying on a single uncertainty measure that conflates OOD detection and generalization, DUL separates these objectives. This decoupling allows for simultaneous optimization of both OOD detection performance (high distributional uncertainty on OOD samples) and OOD generalization (maintaining low overall uncertainty). This is a significant departure from existing methods that often sacrifice one for the other, resulting in a dual-optimal solution. The framework’s theoretical justification highlights its effectiveness in overcoming the “sensitive-robust” dilemma, demonstrating its ability to enhance OOD detection without compromising robustness to distributional shifts. The Bayesian perspective adopted by DUL offers a principled way to disentangle these objectives leading to superior results in empirical evaluations.
Dual Optimality#
The concept of “Dual Optimality” in the context of out-of-distribution (OOD) detection suggests a method that simultaneously excels in two often-conflicting objectives: sensitive OOD detection and robust OOD generalization. Traditional approaches prioritize one over the other, creating a trade-off. A dual-optimal method aims to break this trade-off by achieving high accuracy in identifying OOD samples while maintaining strong performance on in-distribution (ID) data, even under noisy or corrupted conditions. Decoupling uncertainty learning is a potential pathway to dual optimality, where separate components of a model focus on OOD identification and ID robustness. This approach could lead to improved model trustworthiness and reliability in real-world scenarios where models inevitably encounter data that differs from their training distribution. The challenge lies in designing a system that effectively balances these often-competing goals, and rigorously evaluating its success across various benchmark datasets and noise conditions.
Generalization Error#
Generalization error, a crucial concept in machine learning, measures a model’s ability to perform well on unseen data after training. A low generalization error indicates strong generalization, meaning the model hasn’t overfit the training data and can accurately predict outcomes on new, independent data points. Conversely, high generalization error suggests overfitting, where the model performs exceptionally well on training data but poorly on unseen data. Factors influencing generalization error include model complexity, dataset size, and the presence of noise or irrelevant features in the training data. Reducing generalization error often involves techniques like regularization, cross-validation, and feature selection, all of which aim to improve the model’s ability to learn underlying patterns rather than memorizing specific instances from the training dataset. Understanding and minimizing generalization error is critical for building robust and reliable machine learning models. The optimal balance between model complexity and data availability is key; an overly simple model may underfit the data, while an overly complex model may overfit, resulting in poor generalization in both scenarios. Furthermore, the nature of the data itself significantly impacts generalization. Noisy or biased data will likely lead to higher generalization error, highlighting the necessity for data cleaning and preprocessing. Hence, a successful model achieves a sweet spot between model capacity and data quality, resulting in reliable predictions on new and unseen data.
Future Work#
Future research directions stemming from this work could explore several promising avenues. Extending the DUL framework to other learning paradigms, beyond classification, is crucial to broaden its applicability. Investigating the impact of different uncertainty quantification methods within DUL, such as those beyond the Bayesian approach, could reveal further performance gains and robustness improvements. A key challenge lies in mitigating the reliance on auxiliary OOD data, a limitation shared by many existing methods. Research focusing on generating synthetic OOD data or leveraging unsupervised learning techniques to learn from unlabeled out-of-distribution samples would be highly beneficial. A theoretical investigation into the generalization error bound, for a wider variety of OOD detection methods, will provide more insight into the ‘sensitive-robust’ dilemma and inspire improved algorithms. Finally, thorough empirical evaluations on more diverse real-world datasets are needed to validate the generalizability and practical efficacy of DUL in real-world deployment scenarios.
More visual insights#
More on figures
This figure demonstrates the dilemma faced by current state-of-the-art (SOTA) out-of-distribution (OOD) detection methods. Subfigure (a) illustrates the three types of data encountered in real-world deployments of machine learning models: in-distribution (ID) data, covariate-shifted OOD data (with noise or corruption), and semantic OOD data (samples not belonging to any known class). Subfigure (b) shows that most SOTA OOD detection methods achieve high performance by sacrificing OOD generalization ability. They operate in a trade-off area, while the proposed method (DUL) achieves both high OOD detection and generalization performance.

Figure 1(a) shows three types of data that machine learning models encounter in the real world: in-distribution (ID) data, covariate-shifted OOD data (with noise or corruption), and semantic OOD data (from unknown classes). Figure 1(b) illustrates the dilemma of current state-of-the-art (SOTA) OOD detection methods. These methods achieve high OOD detection performance but sacrifice OOD generalization ability. The figure uses a trade-off area graph to depict this balance.
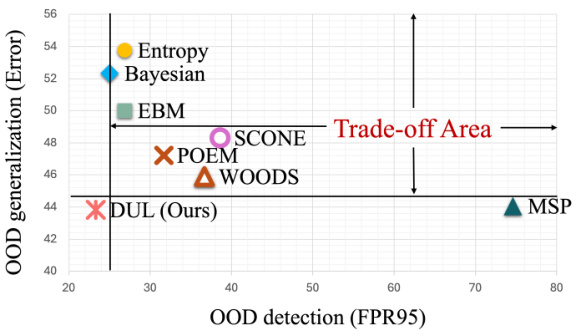
This figure visualizes the different types of uncertainty estimated by the Decoupled Uncertainty Learning (DUL) method. It shows the distributions of data uncertainty, distributional uncertainty, and total uncertainty for three different model training scenarios: a pretrained model, a model finetuned without DUL, and a model finetuned with DUL. The distributions are shown for both in-distribution (ID) and out-of-distribution (OOD) data, allowing for a comparison of how DUL affects the various uncertainty measures, particularly in relation to OOD detection and generalization.

This figure demonstrates the challenges in out-of-distribution (OOD) detection and generalization. (a) shows the different types of data encountered during model deployment, including in-distribution (ID) data, covariate-shifted OOD data (noisy or corrupted), and semantic OOD data (from completely different classes). (b) illustrates the trade-off dilemma that state-of-the-art (SOTA) OOD detection methods face. These methods achieve high OOD detection performance but at the cost of sacrificing OOD generalization ability.
More on tables
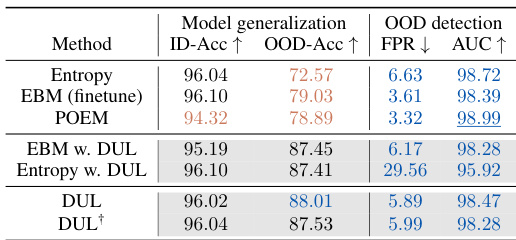
This table compares the performance of various OOD detection methods, including the proposed DUL, across different datasets. It shows ID accuracy, OOD accuracy (generalization), false positive rate at 95% true positive rate (FPR95), AUROC, and AUPR. Improvements and degradations compared to a baseline method (MSP) are highlighted. The table emphasizes DUL’s superior OOD detection performance without sacrificing generalization, a key advantage over other methods.

This table compares the performance of various OOD detection methods, including the proposed DUL, across different datasets. It evaluates both OOD detection performance (FPR, AUROC, AUPR) and OOD generalization ability (OOD accuracy). The table highlights methods that significantly improve or degrade performance compared to a baseline (MSP), emphasizing DUL’s unique ability to achieve state-of-the-art OOD detection without sacrificing generalization.

This table compares the performance of various OOD detection methods, including the proposed DUL, across different datasets and metrics. It highlights the trade-off often seen between OOD detection accuracy and generalization ability, showing that DUL is the only method to achieve state-of-the-art OOD detection without sacrificing generalization performance. The table provides ID accuracy, OOD accuracy, FPR95, AUROC, and AUPR values for each method. Significant improvements or degradations compared to a baseline method are color-coded.

This table compares the performance of various OOD detection methods, including the proposed DUL method, across different datasets. It evaluates both OOD detection performance (FPR, AUROC, AUPR) and OOD generalization ability (OOD accuracy). The table highlights the unique advantage of DUL, which achieves state-of-the-art OOD detection without sacrificing generalization performance, a key issue addressed in the paper.

This table compares the performance of various OOD detection methods across different datasets. It highlights the trade-off between OOD detection and generalization ability, showing that many state-of-the-art methods achieve high detection performance by sacrificing generalization ability. The table showcases the proposed DUL method, which uniquely achieves state-of-the-art OOD detection without compromising generalization.
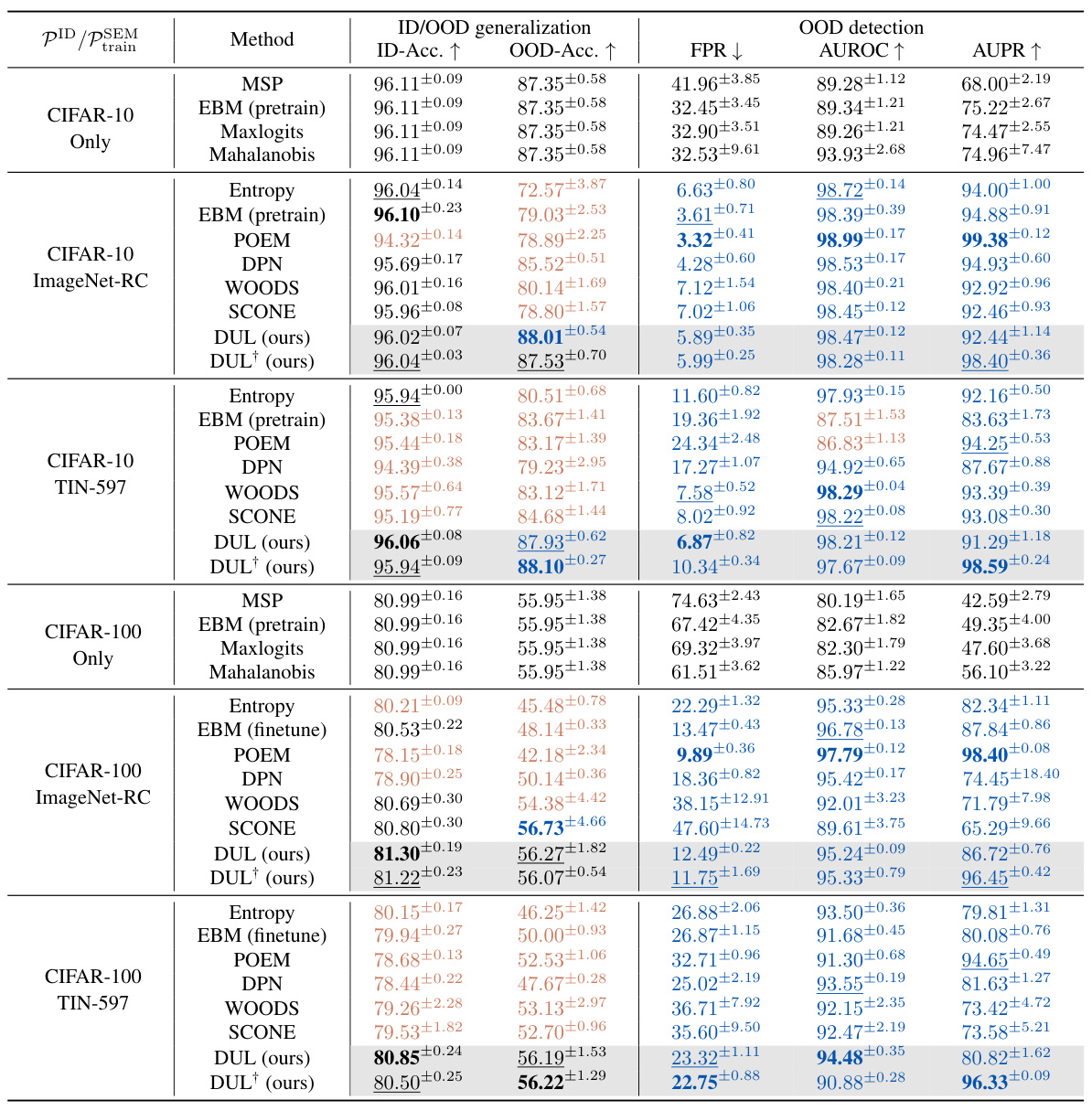
This table compares the performance of various OOD detection methods, including the proposed DUL method, across different datasets. It shows ID accuracy, OOD accuracy (generalization), false positive rate at 95% true positive rate (FPR95), AUROC, and AUPR. The table highlights the superior performance of DUL in achieving state-of-the-art OOD detection without sacrificing OOD generalization ability, a key challenge addressed in the paper. Significant improvements and degradations relative to the baseline method are indicated.

This table compares the performance of various OOD detection methods, including the proposed DUL method, across different datasets. It evaluates both OOD detection performance (FPR, AUROC, AUPR) and OOD generalization ability (OOD-Acc) and shows that DUL achieves state-of-the-art detection performance without sacrificing generalization, unlike other methods that trade-off one for the other. The comparison includes baseline methods and other state-of-the-art techniques.

This table compares the performance of various OOD detection methods, including the proposed DUL, across different datasets. The metrics used are ID accuracy, OOD accuracy, false positive rate at 95% true positive rate (FPR95), AUROC, and AUPR. The table highlights the unique advantage of DUL, achieving state-of-the-art OOD detection without compromising OOD generalization ability, as indicated by the blue and black color coding.

This table presents the results of the proposed Decoupled Uncertainty Learning (DUL) method on various individual OOD detection test datasets. It breaks down the performance (FPR and AUROC) for each dataset, offering a granular view of DUL’s effectiveness across diverse outlier distributions. This level of detail goes beyond the aggregate results and provides stronger evidence supporting the method’s robustness.

This table presents a comparison of OOD detection and generalization performance across various methods. It highlights the trade-off between detection and generalization ability often observed in other methods, where high detection accuracy comes at the cost of lower generalization accuracy, especially in noisy environments. The table showcases that the proposed DUL method uniquely achieves state-of-the-art OOD detection without sacrificing generalization performance.
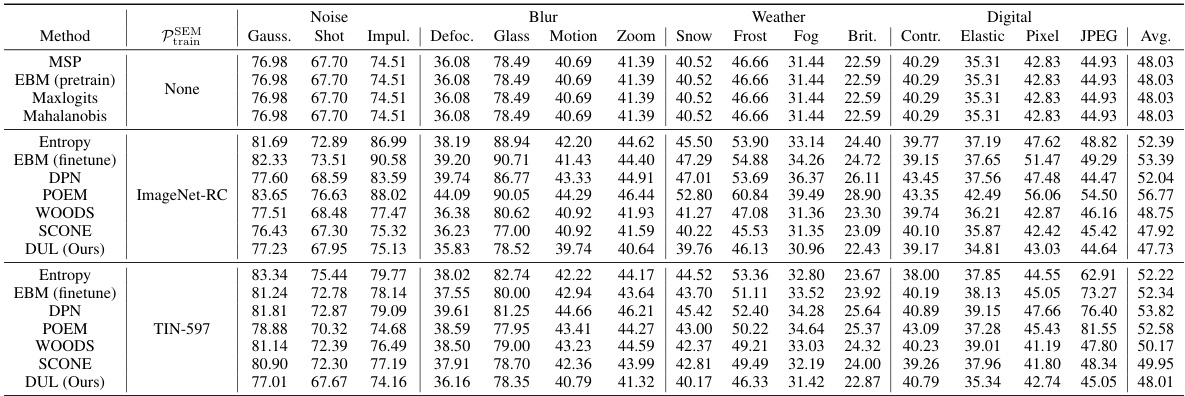
This table presents a comparison of various OOD detection methods, including the proposed DUL method, across different datasets and metrics. It highlights the trade-off between OOD detection accuracy and generalization performance, emphasizing DUL’s unique ability to achieve state-of-the-art results without sacrificing generalization. The table uses color-coding to indicate significant improvements or degradations compared to a baseline method, and bolded/underlined entries show top performers.

This table compares the performance of various OOD detection methods, including the proposed DUL method, across different datasets. It evaluates both OOD detection performance (FPR95, AUROC, AUPR) and OOD generalization ability (OOD-Acc). The table highlights methods that significantly improve or degrade performance compared to a baseline method (MSP). A key finding is that DUL achieves state-of-the-art OOD detection without sacrificing generalization ability.

This table compares the performance of various OOD detection methods, including the proposed DUL, across three different datasets (CIFAR-10, CIFAR-100, and ImageNet-200). It evaluates both OOD detection (FPR95, AUROC, AUPR) and OOD generalization (OOD-Acc). The baseline method (MSP) is a model trained without OOD detection regularization. The table highlights significant improvements or degradations in performance compared to the baseline and shows that DUL achieves state-of-the-art OOD detection without compromising generalization performance.

This table compares the performance of various OOD detection methods, including the proposed DUL, across different datasets. It shows ID accuracy, OOD accuracy, false positive rate at 95% true positive rate (FPR95), AUROC, and AUPR. The table highlights the unique advantage of DUL in achieving state-of-the-art OOD detection without compromising generalization ability. Significant improvements or degradations compared to a baseline method (MSP) are visually indicated.

This table compares the performance of various OOD detection methods, including the proposed DUL method, across different datasets. It shows ID accuracy, OOD accuracy, false positive rate at 95% true positive rate (FPR95), AUROC, and AUPR. The table highlights methods that significantly improve or worsen performance compared to a baseline method (MSP) and indicates which methods achieve state-of-the-art OOD detection without sacrificing generalization ability.
Full paper#