Rethinking Fourier Transform from A Basis Functions Perspective for Long-term Time Series Forecasting

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in time series forecasting because it offers a novel perspective on Fourier transforms, addressing limitations of existing methods. It proposes a new method that improves accuracy and interpretability, opening avenues for further research in deep learning for time series analysis. This is particularly important given the recent interest in utilizing deep learning models to improve the accuracy of long-term forecasting.

Visual Insights

#

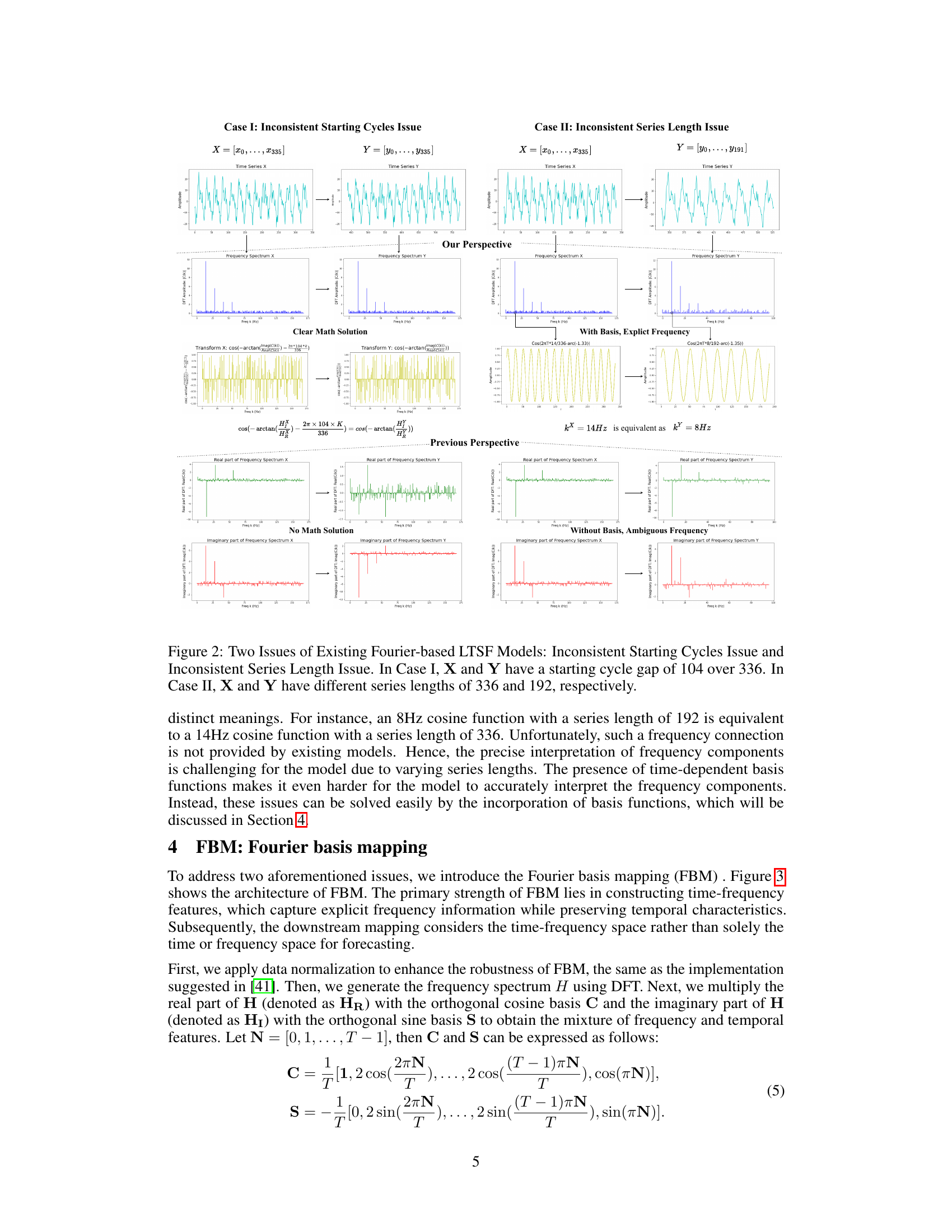
This figure compares existing Fourier-based methods with the proposed Fourier Basis Mapping (FBM) method. Existing methods primarily operate in the frequency domain, transforming time series data and then applying a mapping network that focuses on frequency features. This often leads to issues like inconsistent starting cycles and series length problems, as highlighted in the figure. In contrast, FBM operates in both the time and frequency domains. It uses Fourier basis expansion, which is a key difference; FBM embeds the discrete Fourier transform (DFT) with basis functions before applying a mapping network. This allows FBM to extract explicit frequency features while preserving temporal characteristics and address the limitations of existing methods.

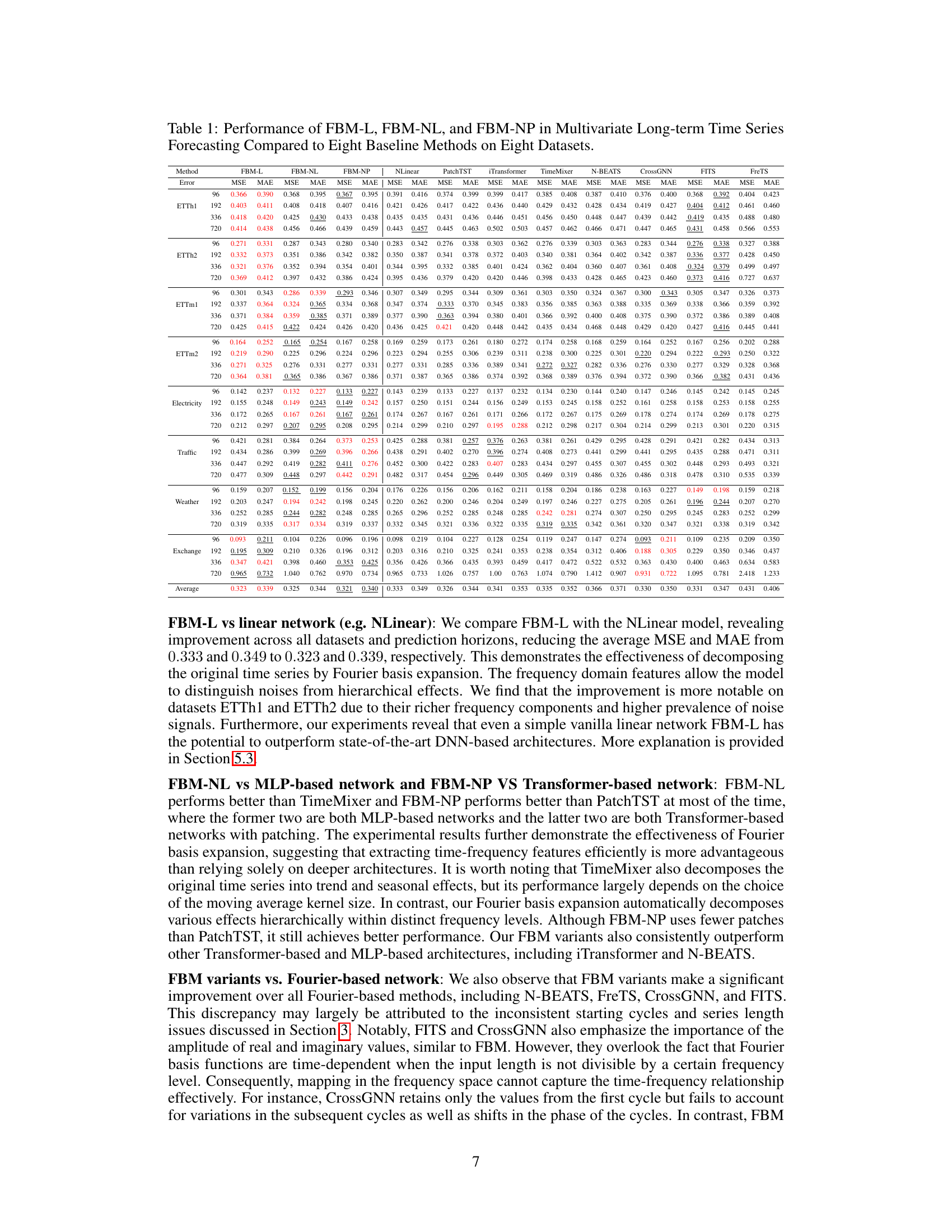
This table presents the results of a comparative study evaluating the performance of three proposed Fourier Basis Mapping (FBM) variants (FBM-L, FBM-NL, FBM-NP) against eight established baseline methods in multivariate long-term time series forecasting. The evaluation is performed across eight real-world datasets with varying forecasting horizons (96, 192, 336, and 720 time steps). The performance metrics used are Mean Squared Error (MSE) and Mean Absolute Error (MAE). The table allows readers to compare the forecasting accuracy of the different methods across different datasets and forecasting horizons.

In-depth insights

#

Basis Function View

#

The ‘Basis Function View’ offers a novel perspective on the Fourier Transform (FT) in time series forecasting. Instead of viewing FT solely as a frequency domain transformation, this viewpoint reframes the real and imaginary components of FT coefficients as coefficients of cosine and sine basis functions. This interpretation reveals a deeper connection between time and frequency domains, highlighting the crucial role of basis functions in interpreting frequency information accurately. This perspective addresses limitations of prior FT-based methods, which fail to fully leverage the temporal dynamics inherently linked to frequency coefficients. The authors argue that the explicit consideration of basis functions leads to more robust and interpretable models, capable of handling inconsistencies related to series length and starting cycles, which are significant challenges in long-term forecasting.

FBM Method

#

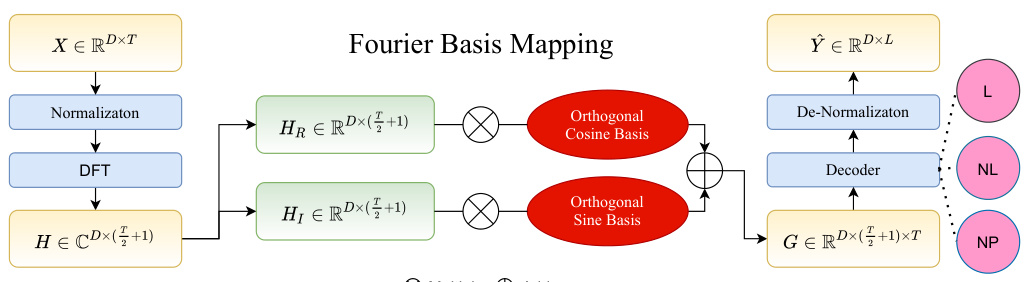
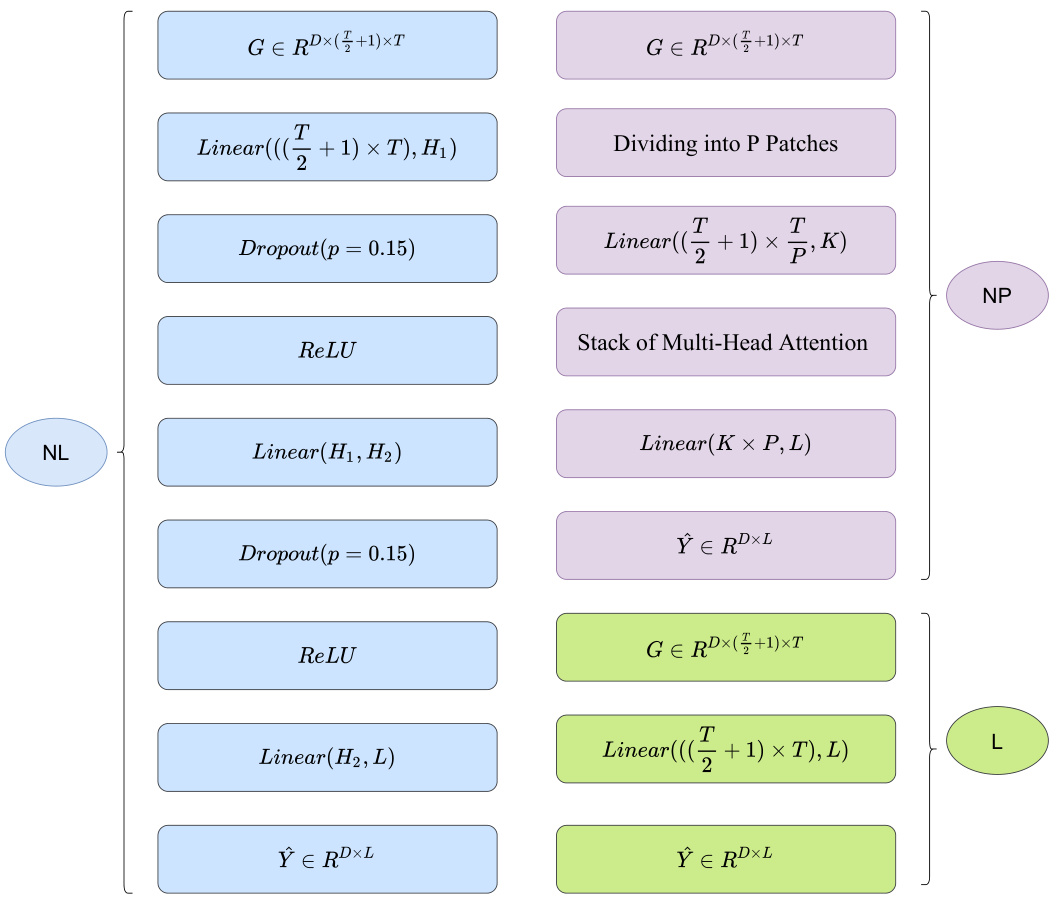
The core of the proposed approach lies in the Fourier Basis Mapping (FBM) method. FBM ingeniously tackles the limitations of existing Fourier-based time series forecasting methods by explicitly incorporating basis functions into the Fourier transform. This crucial step allows for a more precise interpretation of frequency coefficients and a more nuanced understanding of the time-frequency relationship. FBM’s simultaneous operation in both the time and frequency domains is a key differentiator, enabling the extraction of explicit time-frequency features. This innovative approach overcomes the issues of inconsistent starting cycles and inconsistent series lengths, which plague many prior methods. Importantly, FBM’s modular design allows for seamless integration with various neural network architectures, enhancing their performance in long-term time series forecasting tasks. The plug-and-play nature of FBM makes it a versatile tool applicable to a wide range of networks, making it a significant advancement in the field.

Time-Freq Features

#

The concept of ‘Time-Freq Features’ represents a powerful paradigm shift in time series analysis, particularly for long-term forecasting. By integrating temporal and frequency-domain information, these features capture the intricate interplay between the cyclical patterns and their evolution over time. This holistic approach surpasses the limitations of traditional methods that primarily focus on either time or frequency alone. The explicit consideration of time-dependent basis functions is crucial for accurately interpreting frequency coefficients, addressing issues like inconsistent starting cycles and series length problems. These features facilitate the mapping of complex time-frequency relationships, enabling more precise and interpretable forecasting models. Therefore, the effectiveness of Time-Freq Features lies in their capacity to improve models’ ability to learn from both time-dependent and frequency-independent information, ultimately leading to more accurate and robust long-term predictions.

LTSF Enhancements

#

The provided text focuses on enhancing long-term time series forecasting (LTSF) by revisiting the Fourier Transform (FT) from a basis function perspective. The core argument is that existing FT-based methods neglect the underlying basis functions, leading to inconsistencies in starting cycles and series lengths. The proposed Fourier Basis Mapping (FBM) method directly addresses this by integrating time and frequency domain features via Fourier basis expansion. This allows for more precise interpretation of frequency coefficients and a better understanding of time-frequency relationships. FBM’s modular design enables seamless integration with diverse neural network architectures, enhancing performance across various models and datasets. The authors demonstrate the method’s efficacy by incorporating FBM into linear, multilayer perceptron-based, transformer-based, and existing Fourier-based networks, showcasing state-of-the-art results. The key contribution lies in FBM’s ability to extract explicit and interpretable time-frequency features, overcoming limitations of prior approaches and paving the way for improved LTSF accuracy.

Future Works

#

Future research directions stemming from this Fourier Basis Mapping (FBM) method for long-term time series forecasting could involve several key areas. Extending FBM to handle multivariate time series presents a significant challenge and opportunity, as real-world datasets often contain multiple interconnected variables. Investigating more sophisticated deep learning architectures beyond simple linear and MLP networks within the FBM framework could unlock further performance gains. A thorough exploration of the optimal choice and design of basis functions beyond sine and cosine is needed, potentially incorporating wavelet transforms or other suitable orthogonal basis sets tailored to specific data characteristics. A comprehensive evaluation across a broader range of datasets is warranted to ascertain FBM’s generalizability and robustness to varying data distributions and noise levels. Finally, developing a more theoretical understanding of FBM’s ability to capture time-frequency relationships and its connections to other established time series methods would strengthen its foundation and guide further development.

More visual insights

#

More on figures

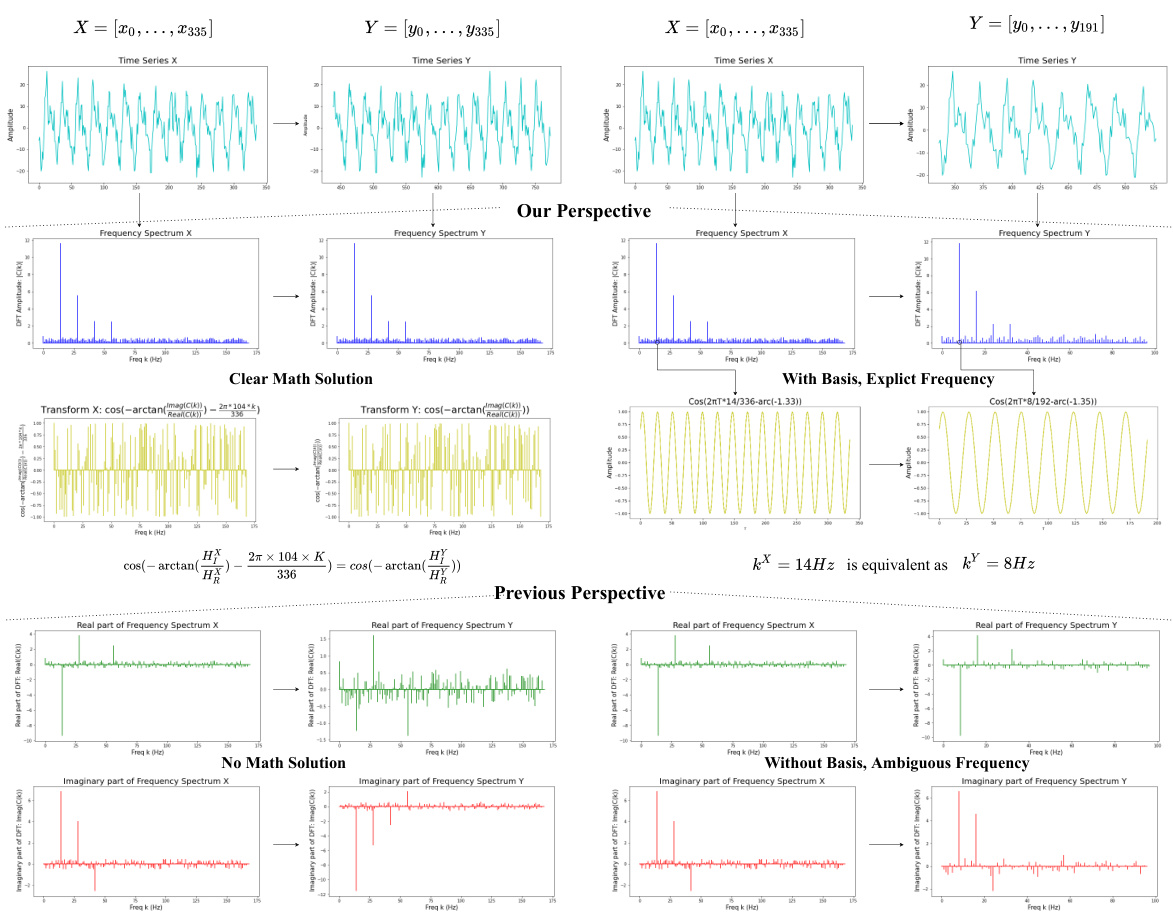
This figure compares existing Fourier-based time series forecasting methods with the proposed Fourier basis mapping (FBM) method. Existing methods mainly process data in the frequency domain, focusing on frequency features alone. In contrast, the FBM method operates in both the time and frequency domains, utilizing time-frequency features. This difference is visually represented in the diagram, showing how FBM incorporates both domains to address limitations of previous approaches such as inconsistent starting cycles and inconsistent series length issues.

This figure compares existing Fourier-based methods with the proposed Fourier basis mapping (FBM) method. Existing methods typically process time series data in the frequency domain, focusing solely on frequency features. In contrast, FBM uniquely operates in both time and frequency domains, extracting time-frequency features for enhanced forecasting performance. The figure illustrates the distinct approaches of existing methods and FBM, highlighting the difference in their focus and data processing techniques.

This figure compares existing Fourier-based time series forecasting methods with the proposed Fourier basis mapping (FBM) method. Existing methods typically process data solely in the frequency domain, mapping frequency features to predictions. In contrast, FBM operates on both time and frequency domains by integrating time and frequency features. This allows for a more comprehensive representation of the data and ultimately leads to improved forecasting.

This figure compares existing Fourier-based methods with the proposed Fourier basis mapping (FBM) method. Existing methods primarily work in the frequency domain, focusing only on frequency features. In contrast, FBM operates in both the time and frequency domains, utilizing time-frequency features. This difference is visually represented to highlight FBM’s unique approach to time series forecasting.

This figure compares the existing Fourier-based methods with the proposed Fourier basis mapping (FBM) method. Existing methods are shown to operate mainly in the frequency domain, mapping only frequency features. In contrast, FBM operates in both time and frequency domains to leverage time-frequency features, addressing limitations like inconsistent starting cycles and series length issues present in existing approaches.

This figure compares existing Fourier-based methods with the proposed Fourier Basis Mapping (FBM) method. Existing methods are shown to operate primarily in the frequency domain, focusing solely on frequency features. In contrast, FBM operates in both the time and frequency domains, leveraging both types of features. The figure highlights the key differences between the approaches, emphasizing FBM’s more comprehensive approach.

This figure compares existing Fourier-based time series forecasting methods with the proposed Fourier Basis Mapping (FBM) method. Existing methods mainly process data in the frequency domain, focusing on frequency features. In contrast, FBM operates in both time and frequency domains, leveraging time-frequency features. The figure highlights how FBM addresses limitations of existing methods, such as inconsistent starting cycles and inconsistent series length, by integrating basis functions and enabling plug-and-play functionality with different neural network architectures.

This figure compares existing Fourier-based methods with the proposed Fourier Basis Mapping (FBM) method. Existing methods typically operate solely in the frequency domain, focusing primarily on frequency features, while FBM operates in both the time and frequency domains by simultaneously considering both time and frequency features. This dual focus enables a more comprehensive understanding of the time-frequency relationships and improves the accuracy and consistency of long-term time series forecasting.

More on tables

This table compares the performance of three proposed Fourier Basis Mapping (FBM) variants (FBM-L, FBM-NL, FBM-NP) against eight baseline methods on eight multivariate long-term time series datasets. The performance is measured using Mean Squared Error (MSE) and Mean Absolute Error (MAE) for different forecasting horizons (96, 192, 336, 720). The table allows for a comparison of the effectiveness of the FBM approach against existing state-of-the-art methods across various architectures (linear, MLP, Transformer, and Fourier-based).

This table presents a comparison of the performance of three variants of the Fourier Basis Mapping (FBM) model (FBM-L, FBM-NL, and FBM-NP) against eight baseline methods for multivariate long-term time series forecasting. The performance is evaluated on eight different datasets using Mean Squared Error (MSE) and Mean Absolute Error (MAE) as metrics for different forecasting horizons. The table allows for a direct comparison of the proposed FBM method against established techniques across various datasets and prediction lengths.

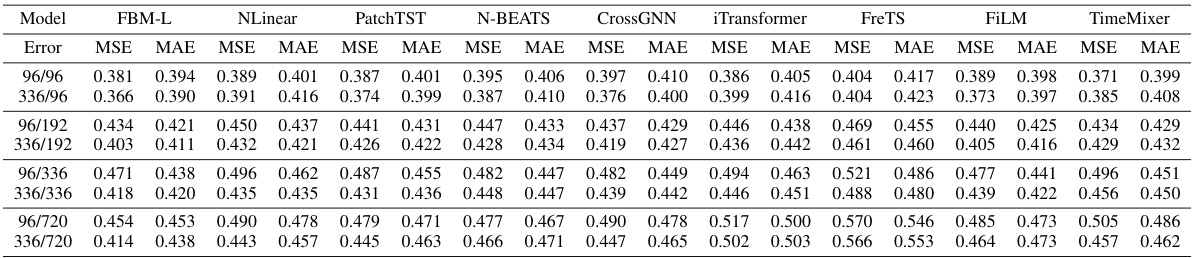
This table presents the Mean Squared Error (MSE) and Mean Absolute Error (MAE) for different forecasting horizons (96, 192, 336, and 720 time steps) on eight multivariate time series datasets. Three variants of the proposed Fourier Basis Mapping (FBM) method (FBM-L, FBM-NL, FBM-NP) are compared against eight baseline methods representing various architectures (linear, transformer-based, MLP-based, and Fourier-based). The results show the performance of the FBM variants across different datasets and forecasting horizons.

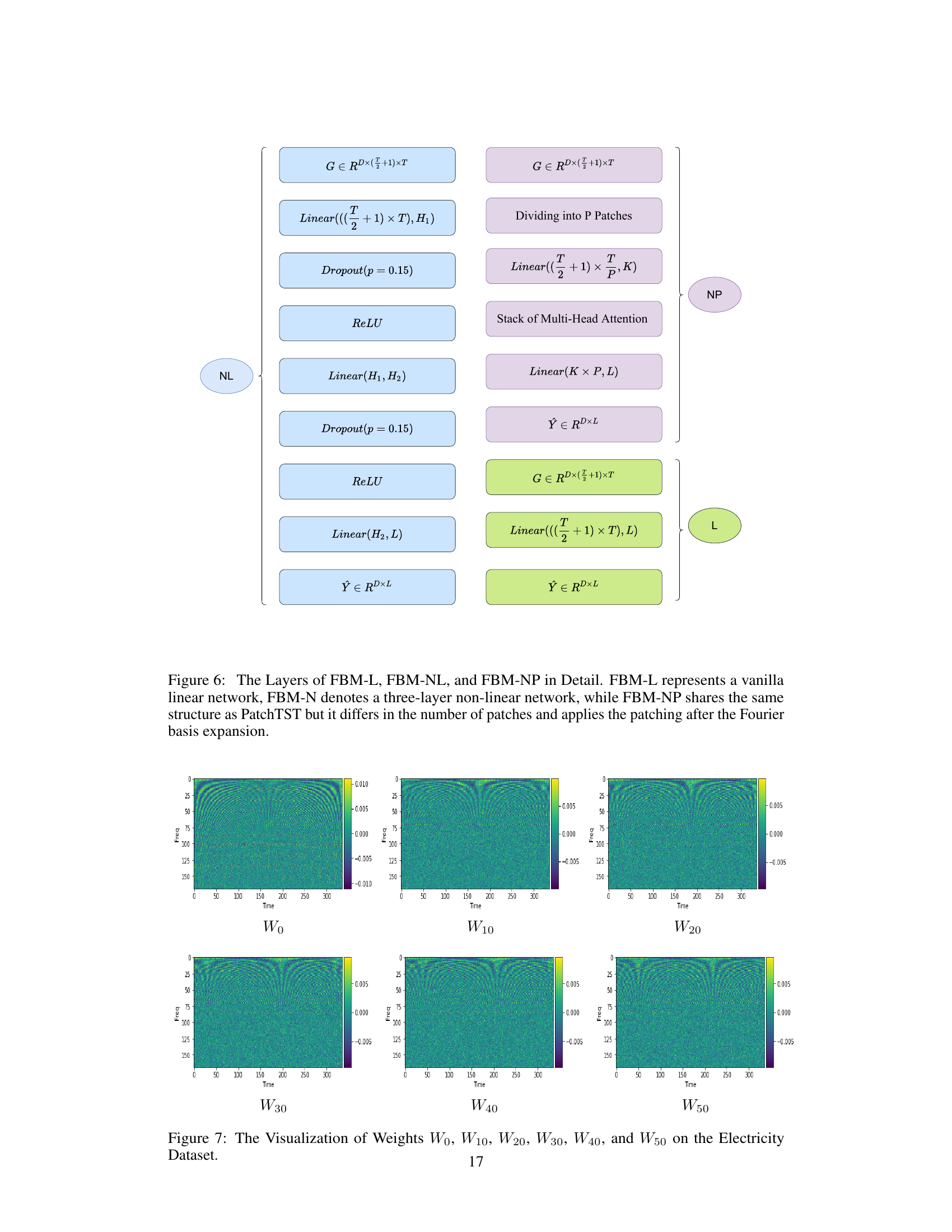
This table presents the hyperparameters used for the three variants of the Fourier Basis Mapping (FBM) model: FBM-NL, FBM-NP, and PatchTST. It shows the values for H1/H2 (number of hidden units in the first/second layer of the MLP network for FBM-NL), and P/K (number of patches and kernel size, respectively, for FBM-NP and PatchTST) used for each dataset. The hyperparameters were selected to optimize the performance of each model on the different datasets.

Full paper

#