↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Large machine learning models are powerful but slow. Early-exit neural networks (EENNs) aim to speed them up by producing predictions from intermediate layers, but ensuring accuracy is crucial. A major challenge is determining when it’s ‘safe’ to exit early without significantly impacting performance. This research addresses this by integrating “risk control” frameworks with EENNs. Risk control is a method that guarantees a certain level of prediction quality before allowing an early exit.
This paper introduces a novel approach to integrate risk control with EENNs, providing a theoretically grounded method to tune the exiting mechanism. They validate their approach on various tasks (image classification, semantic segmentation, language modeling, image generation, etc.), demonstrating significant computational savings while maintaining user-specified performance levels. The method is lightweight and can be applied post-hoc to already trained models, making it practical for real-world implementation. They also improve on prior work for language modeling by enabling less conservative early exiting and achieving larger efficiency gains.
Key Takeaways#
Why does it matter?#
This paper is crucial because it offers a practical solution to a significant challenge in machine learning: the computational cost of large models. By introducing risk control into early-exit neural networks, it enables faster inference without sacrificing accuracy. This is highly relevant to resource-constrained applications and addresses current trends towards more efficient AI. The work opens doors for further research on enhancing the safety and efficiency of early-exit models, especially in safety-critical applications.
Visual Insights#

This figure shows the accuracy and Brier score for four different early-exit neural networks (EENNs) on the ImageNet image classification task. Each EENN allows for predictions at different intermediate layers (’exits’). The x-axis represents the exit layer (1 to 5, with 5 being the final layer), the top graph plots the accuracy at each exit layer and the bottom graph plots the Brier score, a measure of uncertainty. The results show that accuracy generally improves as the network progresses to deeper layers, while uncertainty (Brier score) decreases. This confirms the hypothesis of marginal monotonicity (Eq. 2) of early exiting, meaning that performance generally improves across exits.
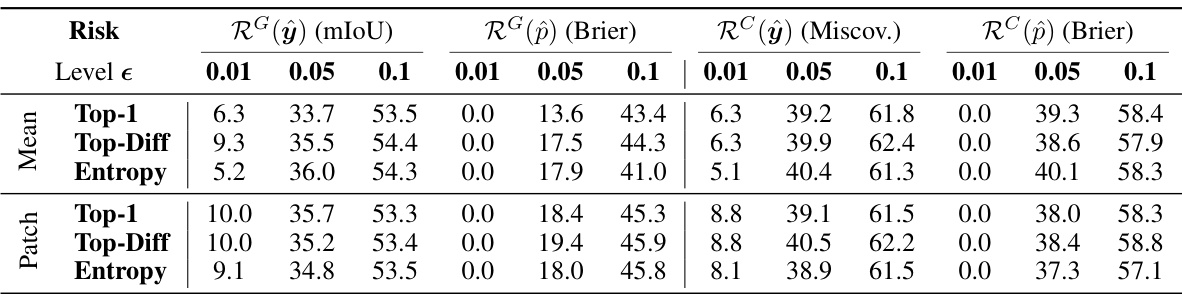
This table presents the efficiency gains achieved by using different risk control methods and confidence measures for semantic segmentation on the Cityscapes dataset. It shows the improvement in mean exit layer and GFLOPS over the last-layer exiting method, while maintaining the user-specified risk level. The results are broken down by different risk types, confidence measures (Top-1, Top-Diff, Entropy), and aggregation methods (Mean, Quantile, Patch).
In-depth insights#
EENN Risk Control#
The core idea of “EENN Risk Control” is to make early-exit neural networks (EENNs) safer and more reliable. EENNs speed up inference by letting the network exit early, but this can hurt accuracy. Risk control methods address this by only allowing an early exit when the model’s confidence is high enough to meet a pre-defined risk level. This ensures that while gaining speed, the performance doesn’t drop below an acceptable threshold. The framework uses statistical methods, particularly risk control techniques, to calibrate the network’s exit decisions. This is done in a post-hoc manner, meaning the risk-control mechanism is added after the EENN is already trained. Various risk functions are defined, focusing both on the accuracy of the model’s predictions and the quality of the underlying predictive distribution, which is helpful in uncertainty estimation. Several approaches, including empirical risk control and more robust methods based on high-probability guarantees, are explored for setting the safety thresholds. This work highlights the importance of both accuracy and uncertainty control in ensuring that speedups don’t come at the cost of reliability, making EENNs suitable for safety-critical applications. The authors demonstrate the effectiveness of their approach across diverse tasks, showing that substantial computational savings are possible without sacrificing user-specified performance standards.
Early-Exit Risks#
The section on “Early-Exit Risks” would delve into the challenges of prematurely exiting a neural network’s computation. The core problem is balancing speed and accuracy: early exits offer substantial computational savings but usually sacrifice predictive performance. This section likely proposes methods to quantify this tradeoff, introducing risk functions that measure the discrepancy between predictions made by early exits and the full network. Two types of risk are likely discussed: Performance Gap Risk, measuring the difference in prediction quality using a loss function, and Consistency Risk, focusing on the uncertainty and consistency between early and full model predictions. This section is crucial as it lays the groundwork for developing effective and safe early-exit mechanisms by providing a framework for quantifying the risk involved and making informed decisions about when early exit is acceptable. A key aspect will likely be the user-specified tolerance for risk, enabling a customizable balance between computational efficiency and accuracy.
Risk Control Methods#
The paper explores risk control within the context of early-exit neural networks (EENNs), focusing on how to ensure that computational speed-ups from early exiting don’t come at the cost of significant performance degradation. Risk control is framed as a post-hoc solution, meaning it’s applied after the EENN is trained, rather than being integrated directly into the model’s architecture. The core idea is to leverage statistical frameworks to carefully select a threshold that determines when it’s “safe” for the network to exit early. The paper proposes and compares two main risk control approaches: controlling risk in expectation and with high probability. The former aims to keep the average risk below a user-specified tolerance level, while the latter provides stronger guarantees by ensuring the risk stays below the threshold with high probability. Different risk functions are introduced to account for both the prediction accuracy and the quality of the predicted uncertainty (distribution). These methods are empirically evaluated across a range of vision and language tasks, showing considerable computational savings without sacrificing performance.
Empirical Results#
The empirical results section of a research paper should present a comprehensive evaluation of the proposed method. It needs to demonstrate the method’s performance across various metrics and datasets. Key aspects include a detailed description of the experimental setup, clear visualization of results (e.g., graphs, tables), and a rigorous statistical analysis. The discussion should highlight the strengths and weaknesses of the method, comparing its performance against existing state-of-the-art techniques. The analysis should also address potential limitations, sources of error, and any unexpected findings. A strong empirical results section should not only support the paper’s claims but also provide valuable insights into the broader implications of the research. It is critical to ensure the reproducibility of the results, possibly by providing clear instructions and possibly open-source code and data.
Future Work#
The authors acknowledge the limitation of using a single shared exit threshold across all layers in their early-exit neural network model, suggesting that relaxing this constraint could lead to further efficiency gains. They also point to the need for exploring risk control techniques for high-dimensional thresholds to handle the increased complexity of multiple thresholds. Future work should focus on adapting the framework to handle multiple thresholds, potentially using techniques like threshold functions to reduce dimensionality. Addressing the i.i.d. assumption on calibration and test data is also crucial, as it limits the applicability to scenarios with distribution shifts. Investigating online updating strategies and developing methods for controlling loss tails rather than expected loss are also promising directions. Finally, exploring the interaction between risk control and other model optimization techniques (such as pruning) to maximize efficiency would be beneficial.
More visual insights#
More on figures
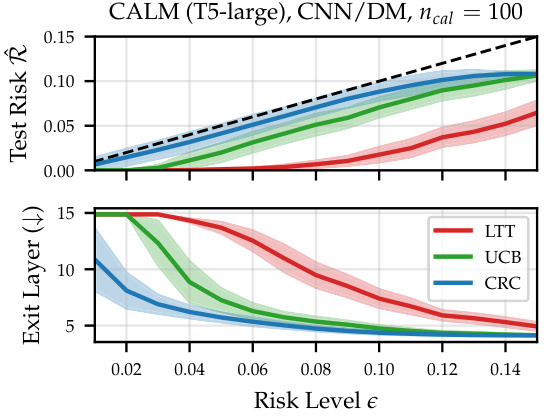
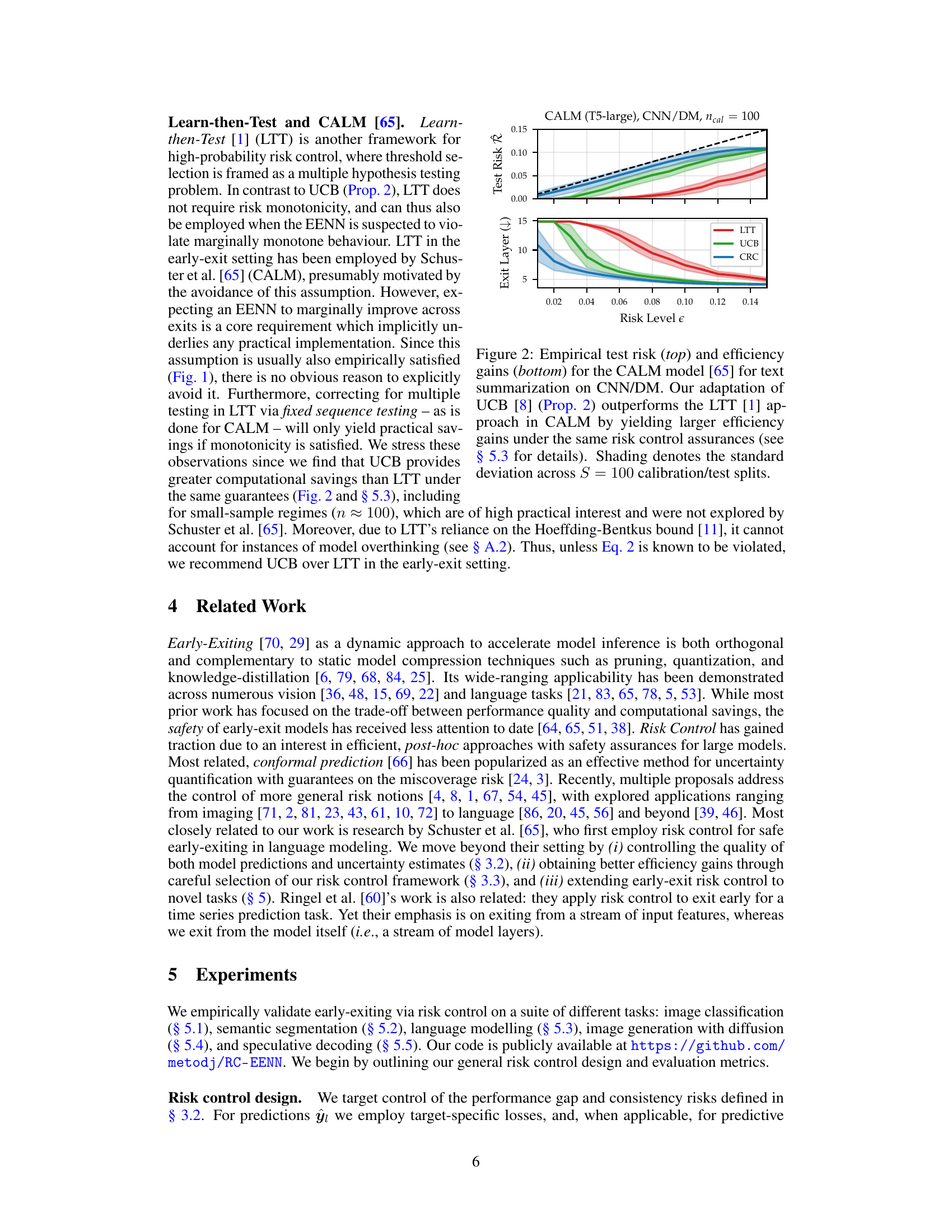
This figure compares the performance of three different risk control methods (LTT, UCB, and CRC) for early-exiting in a text summarization task. The top panel shows the test risk, a measure of how well the model performs relative to a fully computed model, while the bottom panel shows the efficiency gains, measured by the average number of layers processed before exiting. The results indicate that the UCB method offers better efficiency gains than the LTT method while maintaining the same level of risk control.

This figure displays the empirical test risk and efficiency gains for four different early-exit models (MSDNet, DVIT, L2W-DEN, Dyn-Perc) across four different risk types and various risk levels (ε) on the ImageNet dataset. The top row shows the test risk, demonstrating that risk control is achieved across all models, risk types and levels. The bottom row illustrates the efficiency gains (in terms of reduced computation), highlighting that substantial computational savings are achieved while maintaining the specified risk levels, whether controlled in expectation or with high probability.

This figure demonstrates the early-exiting mechanism of the proposed method on the Cityscapes dataset. It shows two example images, one with an early exit and one with a late exit. For each example, it displays the ground truth segmentation mask, the confidence map at the first and last model layers, and the Brier loss difference between the first and last layers stratified across the different exit layers. The left panel provides boxplots summarizing the Brier loss difference across all samples for each exit layer. The right panel visually shows the confidence maps for the early and late exits, compared to the ground truth.

This figure shows the results of applying early-exit diffusion with the DeeDiff model on the CIFAR dataset. The left side displays generated images at various risk levels (ϵ), demonstrating how image quality degrades as the risk tolerance increases. The right side presents graphs illustrating that the empirical test risk is successfully controlled across different risk levels using both CRC and UCB risk control methods. The top graph shows that the risk increases with less stringent thresholds. The bottom graph shows that the average exit point decreases with higher risk levels, indicating more computational savings but a possible trade-off in image quality.
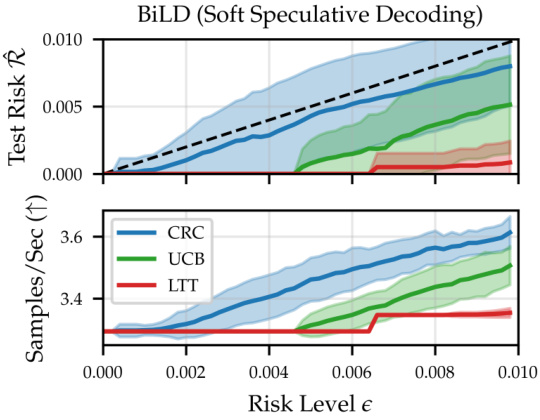
This figure shows the empirical test risk and efficiency gains for the BiLD model, a soft speculative decoding method for large language models, when applying risk control to the rollback threshold. The upper plot shows how the test risk increases with the risk level (epsilon) for different risk control methods (CRC, UCB, and LTT). The lower plot demonstrates the speedup in samples per second achieved by each method. The results indicate that UCB outperforms LTT in terms of efficiency gains while maintaining the same level of risk control.
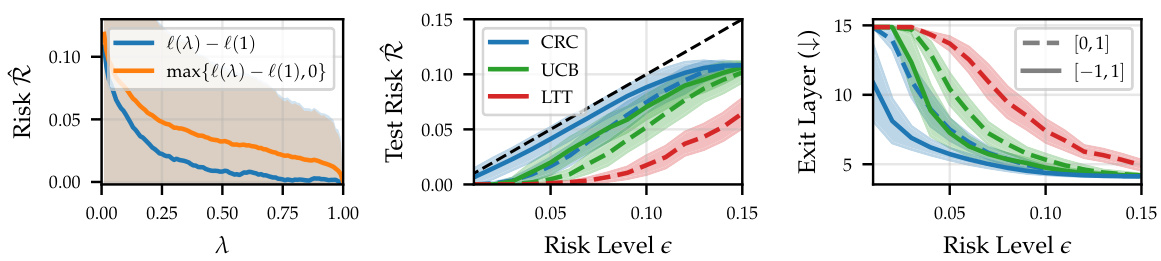
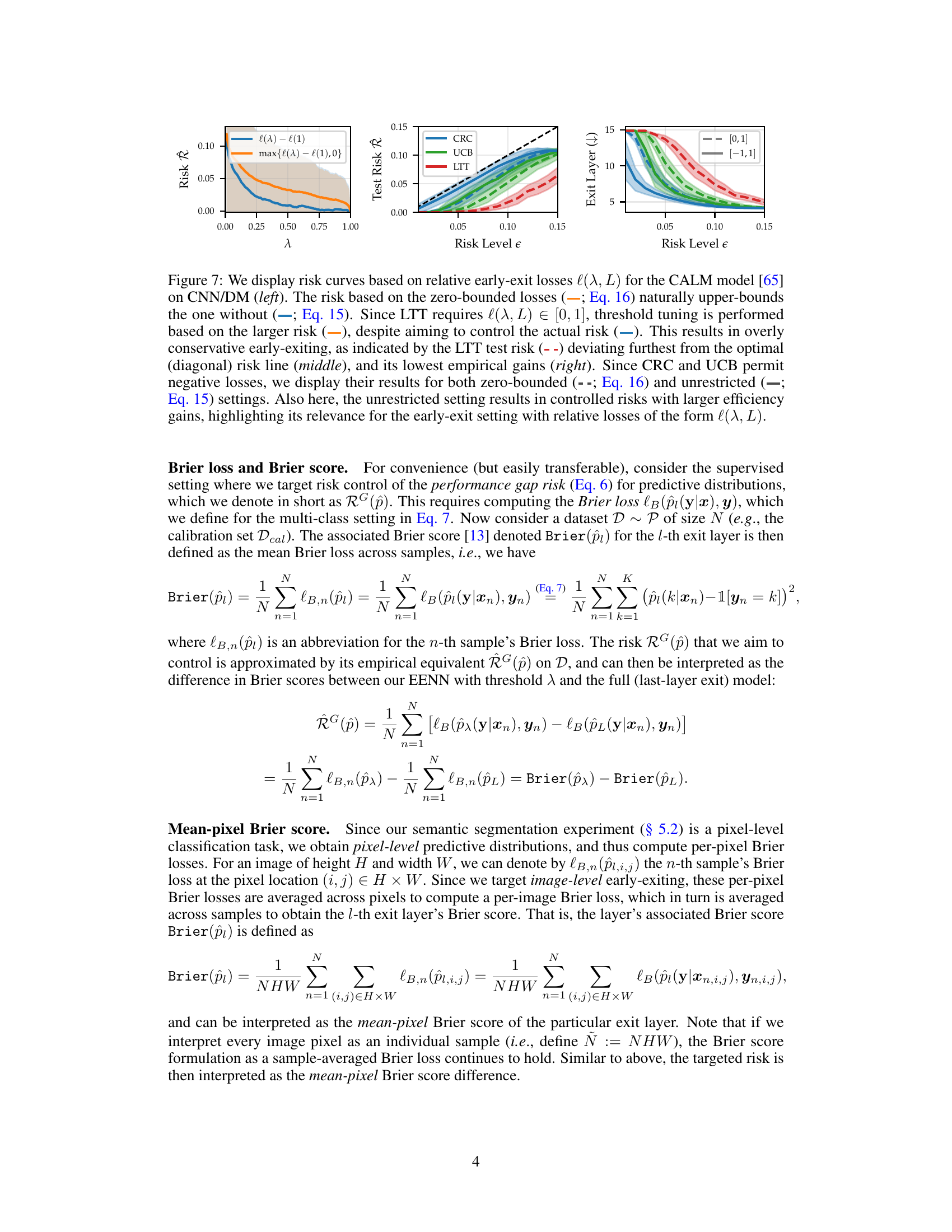
The figure compares three different risk control approaches (CRC, UCB, and LTT) for early-exit neural networks on the CNN/DM dataset. It shows how the choice of loss function and the method for risk control affect the relationship between the risk level and the model’s performance. Specifically, the figure demonstrates that using the zero-bounded loss (max{l(λ) - l(1), 0}) results in more conservative early-exiting compared to using the unrestricted loss (l(λ) - l(1)), which is particularly noticeable for the LTT method. The figure’s three panels visualize the empirical risk, test risk, and average exit layer across different risk levels. The results highlight that methods capable of handling negative losses (CRC and UCB) achieve better efficiency gains while maintaining a controlled risk.

This figure shows the results of applying different risk control methods (CRC and UCB) to various early-exit neural networks for image classification on the ImageNet dataset. The top row displays the test risk for different risk levels (epsilon) and risk types (performance gap and consistency). The bottom row shows the efficiency gains (in terms of reduced number of layers evaluated) for the same settings. The results demonstrate that the proposed risk control approaches successfully control the test risk while achieving significant computational savings.
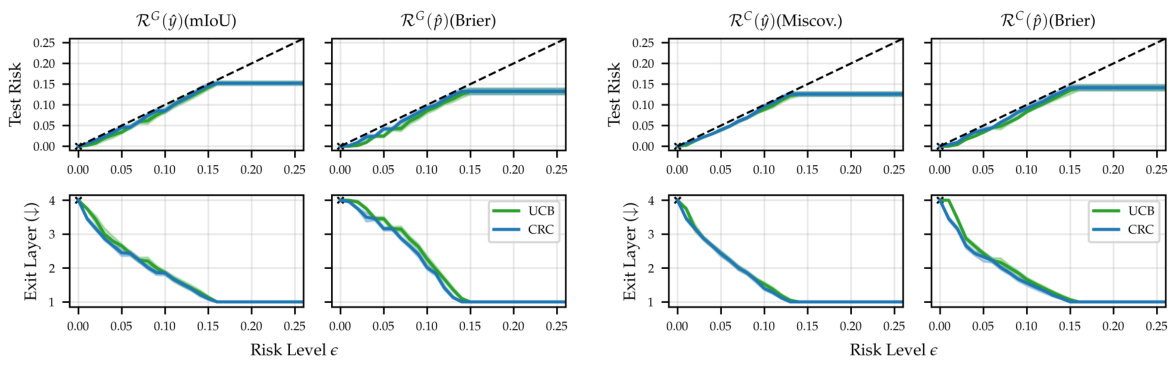
This figure shows the empirical test risk and efficiency gains for various early-exit models on the ImageNet dataset using different risk control methods. The top row displays the test risk for four different risk measures (Performance Gap for predictions and distributions, Consistency Risk for predictions and distributions) at various risk levels (epsilon). The bottom row presents the corresponding efficiency gains (reduction in the number of layers needed for inference). The results demonstrate that the proposed risk control methods effectively maintain the desired risk level across models and risk types while achieving substantial computational savings.
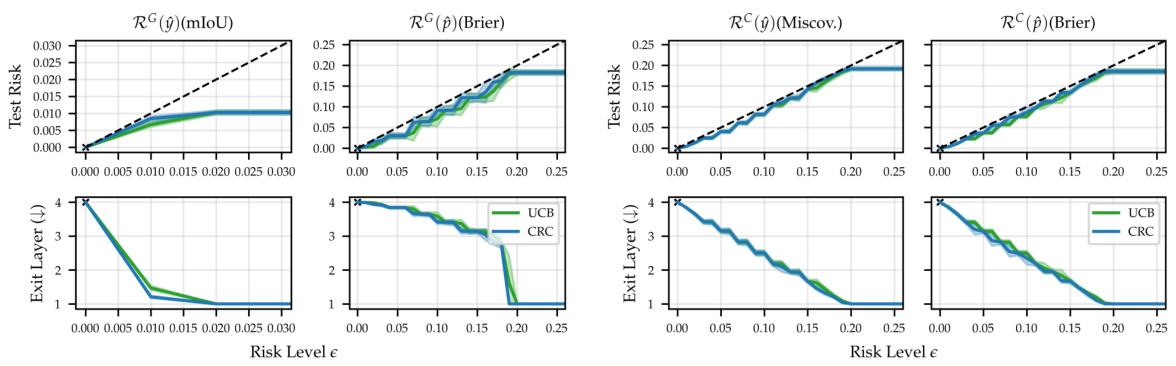
This figure displays the empirical test risk and efficiency gains for four different early-exit models on the ImageNet dataset. The top row shows the test risk for four different risk measures (performance gap risk for predictions, performance gap risk for distributions, consistency risk for predictions, and consistency risk for distributions) and varying risk levels (epsilon). The bottom row shows the corresponding efficiency gains, represented by the average exit layer. The results demonstrate that the test risk is controlled across all models, risk types, and risk levels, and that substantial efficiency gains are achieved despite the strong risk control guarantees.
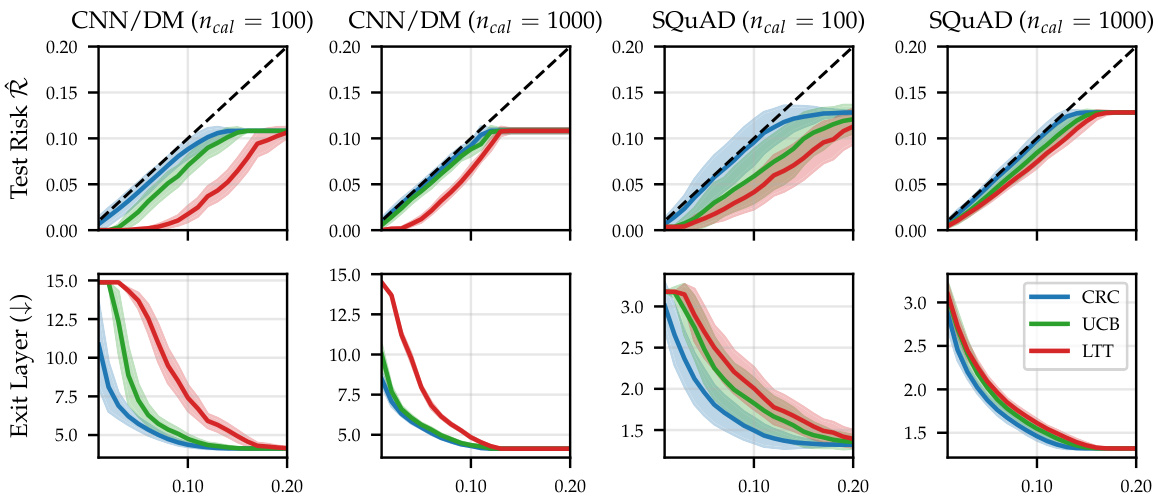
This figure displays the results of applying different risk control methods (CRC, UCB, LTT) to early-exit language models for text summarization and question answering tasks. The top row shows the test risk, while the bottom row displays the efficiency gains. The results show that UCB outperforms LTT, offering greater efficiency gains while maintaining similar levels of risk control.

This figure compares the performance of three different confidence measures (state saturation, meta-classifier, and softmax) for the CALM model in text summarization tasks. It evaluates the risk control and efficiency gains using different risk control frameworks (CRC, UCB, and LTT) across various risk levels. The results demonstrate that the proposed CRC and UCB methods consistently achieve better efficiency gains compared to LTT, while maintaining the desired level of risk control, across all the confidence measures.

This figure shows the results of early-exit diffusion using the DeeDiff model on the CIFAR dataset. The left side displays generated images for different risk control levels (ε). As ε increases, the quality of the generated images decreases, demonstrating the trade-off between computational efficiency and image quality. The right side shows that the empirical test risk is controlled for both CRC and UCB methods, indicating that the proposed risk control framework successfully maintains the desired level of risk, even with early exits.
More on tables

This table presents the efficiency gains achieved by different Early-Exit Neural Networks (EENNs) on the ImageNet dataset when employing risk control methods. It shows the relative improvement in the average exit layer (and thus computational savings) for various risk levels (epsilon) and calibration set sizes, using two different risk control approaches (CRC and UCB). The table is separated into four parts, each illustrating a combination of risk metric (performance gap or consistency) and risk control method.
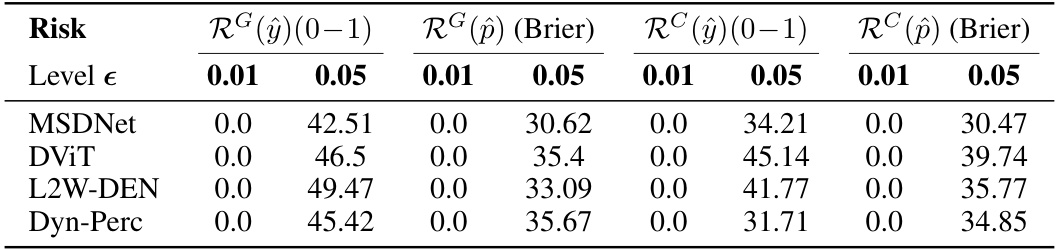
This table shows the efficiency gains achieved by different early-exit neural network models on the ImageNet dataset for various risk control levels. The efficiency gains are measured as the relative improvement in the mean exit layer compared to a full network evaluation. The table considers different risk metrics and model architectures, providing a comprehensive evaluation of the proposed risk control method’s effectiveness.

This table shows the efficiency gains achieved by different Early-Exit Neural Networks (EENNs) on the ImageNet dataset when employing risk control methods. The gains are presented as the percentage improvement in the average exit layer compared to a model using the full network. Two risk control methods are compared: Conformal Risk Control (CRC) and Upper Confidence Bound (UCB), each tested with calibration set sizes of 100 and 1000. The table is broken down by risk type (performance gap and consistency, both for predictions and distributions), and shows the results for different risk levels (0.01 and 0.05).
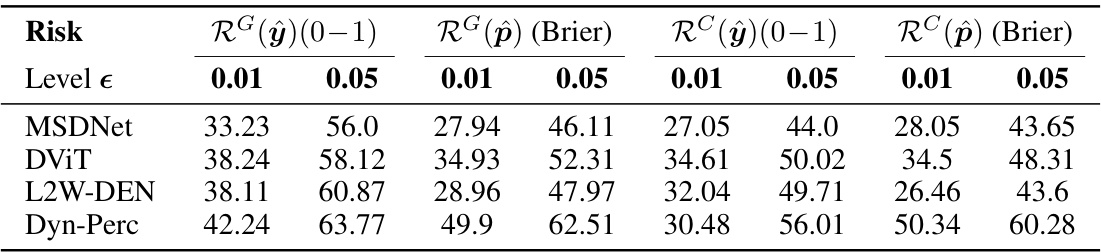
This table shows the efficiency gains achieved by different Early-Exit Neural Networks (EENNs) on the ImageNet dataset when using risk control. The efficiency is measured as the relative improvement in the mean exit layer compared to a full network. Two risk control methods, CRC and UCB, are compared at two different calibration set sizes (n=100 and n=1000). Results for low risk levels (0.01 and 0.05) are highlighted, as these are more relevant in practical applications.
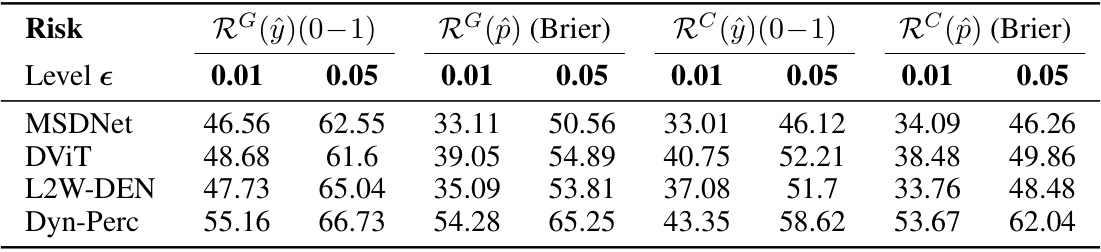
This table presents the efficiency gains achieved by different early-exit neural networks (EENNs) on the ImageNet dataset. The gains are calculated as the relative improvement in the mean exit layer compared to a full model, after applying risk control techniques (CRC and UCB) to manage the risk of early-exiting. Results are shown for different risk levels (epsilon) and calibration set sizes. The focus is on small risk levels (0.01 and 0.05) which are more relevant to practical applications.

This table presents the efficiency gains achieved by using the proposed risk control method for semantic segmentation on the Cityscapes dataset. It shows the improvements in terms of mean exit layer and GFLOPS, categorized by different risk types, confidence measures, and risk levels. The results demonstrate the effectiveness of the method while maintaining controlled risk levels.

This table presents the efficiency gains achieved using different risk control strategies for semantic segmentation on the Cityscapes dataset. It shows the improvement in terms of the average number of layers processed and the number of floating-point operations (FLOPS) compared to using the full model. Various risk levels, confidence measures, and risk types are used to assess the impact on efficiency. The test risk is consistently controlled in all scenarios.
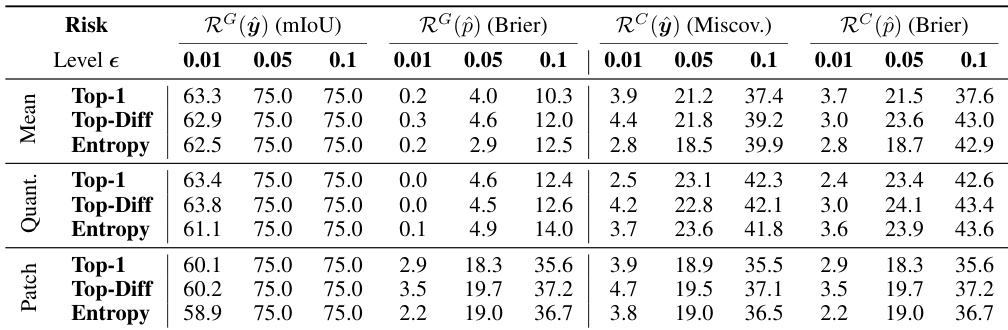
This table presents the efficiency gains obtained from using different risk control methods and confidence measures for semantic segmentation on the Cityscapes dataset. It shows improvements in mean exit layer and GFLOPS, indicating faster inference speeds while maintaining controlled risk levels.

This table presents the efficiency gains achieved by different early-exit neural network models on the ImageNet dataset when employing risk control methods. It shows the relative improvement in the average exit layer (and thus computational speedup) compared to using the full model, for various risk levels (0.01 and 0.05) and different risk control techniques (CRC and UCB). The results are presented separately for different model architectures (MSDNet, DVIT, L2W-DEN, Dyn-Perc) and for two different calibration set sizes (n=100 and n=1000). The table demonstrates that substantial efficiency gains can be obtained even while maintaining the specified risk level.
Full paper#