↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many applications require sets of structurally diverse graphs for tasks like algorithm testing. However, generating such graphs is challenging because existing random graph models produce similar structures. This paper tackles this challenge by introducing a new method.
The paper proposes a novel diversity measure, Energy, and compares various algorithms: a greedy approach, genetic algorithm, local optimization, and a neural generative model. The researchers found that the choice of graph distance measure significantly affects the characteristics of the generated graphs, and their proposed methods can significantly improve graph diversity compared to standard techniques.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses a significant gap in graph generation research by focusing on structural diversity, a previously unexplored aspect. Its proposed methods and diversity metrics are directly applicable to various graph-related tasks, such as algorithm testing and neural network evaluation, thus potentially impacting a wide range of fields.
Visual Insights#

This figure shows a sample of 24 graphs generated using the methods described in the paper. The graphs illustrate the diversity of structures that can be produced, showcasing variations in density, connectivity, cycles, and overall topology. This visual representation highlights the effectiveness of the proposed algorithms in generating structurally diverse graphs, a key aspect of the paper’s contribution.
This table presents the Energy optimization results for different methods of generating diverse graphs, using four graph distance measures (GCD, Portrait-div, NetLSD-heat, NetLSD-wave). It compares various approaches, including baselines (ER-mix, GraphWorld, Random Graph Generators) and combinations of greedy, genetic, and local optimization algorithms, against the performance of an iterative graph generative modeling (IGGM) approach. Lower values indicate higher diversity.
In-depth insights#
Graph Diversity Metrics#
Measuring graph diversity is crucial for various applications, yet it presents unique challenges. A key aspect is defining appropriate graph distance metrics, which quantify the dissimilarity between graph structures. The choice of metric significantly impacts the perceived diversity, as different metrics emphasize various structural properties (e.g., degree distribution, clustering, or subgraph counts). Energy, a proposed metric, addresses limitations of existing measures by satisfying monotonicity and uniqueness properties, ensuring a more robust assessment of diversity. However, the computational cost of evaluating certain graph distance metrics can be substantial, demanding consideration when dealing with large graphs or large sets of graphs. Further research is essential to explore the interplay between different graph distance metrics and their effectiveness in revealing structural diversity for specific applications. Ultimately, the selection of a graph diversity metric should be guided by the specific characteristics relevant to the problem domain and computational constraints.
Generative Models#
Generative models for graphs are crucial for various applications, from testing graph algorithms to creating realistic network datasets. This paper explores the challenge of generating structurally diverse graphs, arguing that existing methods often produce similar structures. The core problem lies in defining and measuring graph diversity, which is non-trivial given the vast space of possible graphs. The authors propose a novel diversity measure called ‘Energy’, satisfying key properties like monotonicity and uniqueness, which are absent in previous metrics. Several algorithms are proposed and compared—greedy, genetic, local optimization, and neural generative modeling— each optimizing the Energy measure. Results demonstrate a significant improvement in diversity compared to baseline random graph models. Importantly, the analysis highlights how different graph distances influence the structural properties of the generated graphs, furthering our understanding of graph dissimilarity.
Greedy Algo Analysis#
A greedy algorithm for generating diverse graphs iteratively adds the graph that maximizes a chosen diversity measure at each step. Theoretical guarantees on diversity are achievable, particularly when the algorithm starts with a sufficiently diverse set of candidate graphs. The greedy approach’s simplicity makes it computationally efficient, requiring fewer graph distance computations compared to more complex algorithms like genetic algorithms. However, a major limitation is its susceptibility to local optima, meaning the algorithm might settle on a suboptimal diverse set. The analysis of the greedy algorithm’s performance often involves analyzing its approximation ratio in terms of the optimal diversity achievable, highlighting the trade-off between efficiency and optimality. It’s crucial to consider the initial graph set, as the greedy algorithm is highly reliant on its diversity to obtain a good result. Careful consideration of the diversity measure is critical, as different measures prioritize diverse features which significantly impacts the resultant graph structures.
Diversity Optimization#
The concept of ‘Diversity Optimization’ in the context of graph generation is crucial for creating representative datasets. The authors grapple with the non-trivial task of defining and measuring diversity, acknowledging the limitations of existing measures and proposing a novel approach based on the energy of a system of charged particles. This approach addresses shortcomings of simpler measures, ensuring both monotonicity and uniqueness in the resulting diversity score. Several algorithms are then proposed and evaluated for optimizing the diversity score, including greedy, genetic, local optimization, and iterative generative modeling. Benchmarking against existing random graph models demonstrates the effectiveness of the proposed techniques in generating significantly more diverse graph sets. The analysis highlights the sensitivity of different graph distances to specific structural properties, offering valuable insights into the properties of various graph distances themselves. The study successfully establishes a novel approach to generating diverse graphs, showcasing a rigorous theoretical foundation combined with robust experimental validation.
Future Research#
The research on generating structurally diverse graphs is in its nascent stages, presenting exciting avenues for future exploration. Scalability remains a significant hurdle; as the number of nodes increases, the computational cost of exploring the vast graph space explodes. Addressing this requires investigating more efficient algorithms, potentially leveraging advanced techniques like graph embeddings or sampling methods to intelligently explore a reduced, yet representative, subset of the space. Furthermore, more sophisticated diversity measures need development, capable of capturing subtle nuances of graph structure beyond current metrics. This involves a deeper investigation into the theoretical properties of graph distances and their suitability for quantifying structural diversity. Finally, exploring the real-world applications of structurally diverse graphs is crucial; their use in algorithm testing, neural network training, and benchmarking graph algorithms offers significant potential, but the efficacy of employing diverse sets in these contexts requires careful investigation.
More visual insights#
More on figures

This figure shows the relationship between the average node degree and the average clustering coefficient in Erdős-Rényi random graphs. The blue dots represent graphs generated with a fixed edge probability p=0.5 (ER-0.5), while the pink crosses represent graphs generated with varying edge probabilities (ER-mix). It illustrates how the Erdős-Rényi model, even with varying parameters, produces graphs with a highly correlated relationship between these two structural properties, limiting their diversity in structural characteristics. The concentration of points for ER-0.5 highlights the limited structural variation produced by a single fixed parameter.
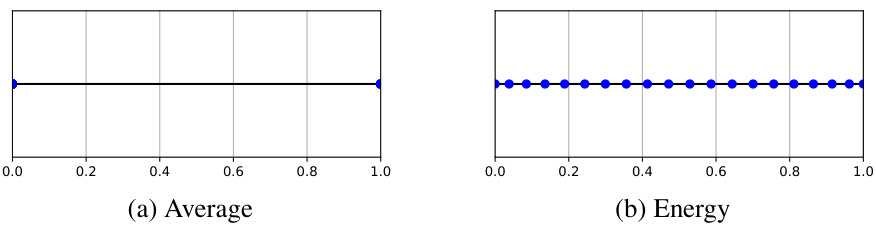
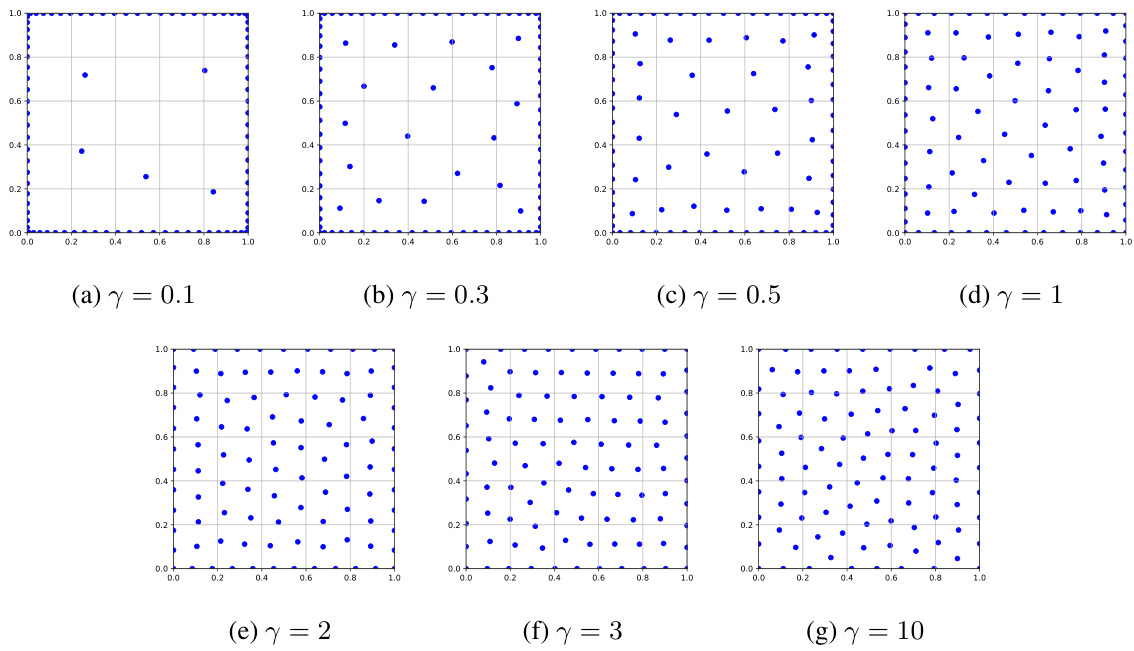
This figure illustrates the results of optimizing two different diversity measures (Average and Energy) on a one-dimensional line segment. The Average measure leads to a degenerate solution where points cluster at the segment’s endpoints. In contrast, the Energy measure results in a more even distribution of points along the segment, demonstrating its effectiveness in promoting diversity.

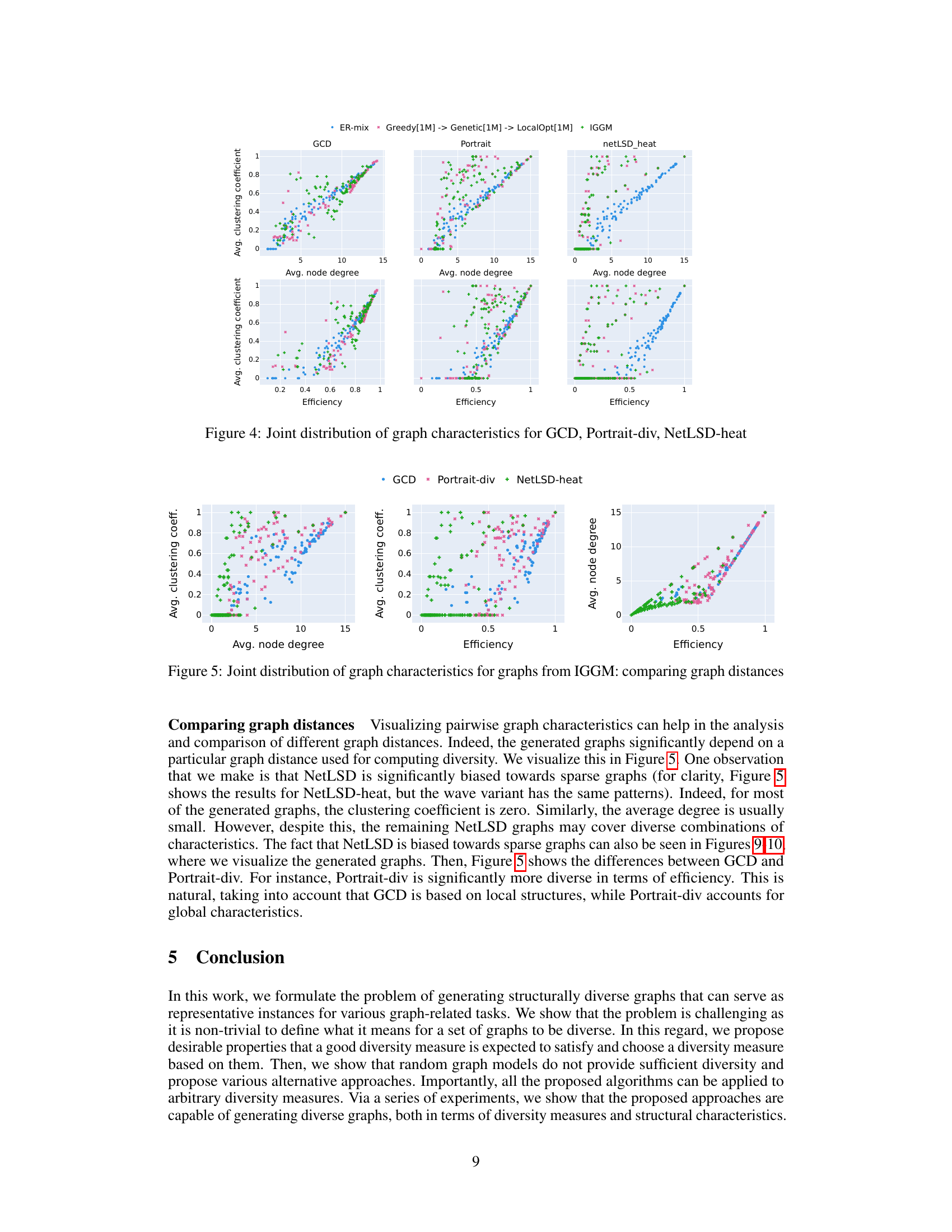
This figure visualizes the joint distribution of several graph characteristics for three different graph distance measures: GCD (Graphlet Correlation Distance), Portrait-div (Portrait Divergence), and NetLSD-heat (NetLSD using heat diffusion). Each subplot shows a scatter plot with one characteristic on the x-axis and another on the y-axis, illustrating their relationships. The plots reveal how the distributions of these structural properties vary depending on the underlying graph distance measure.
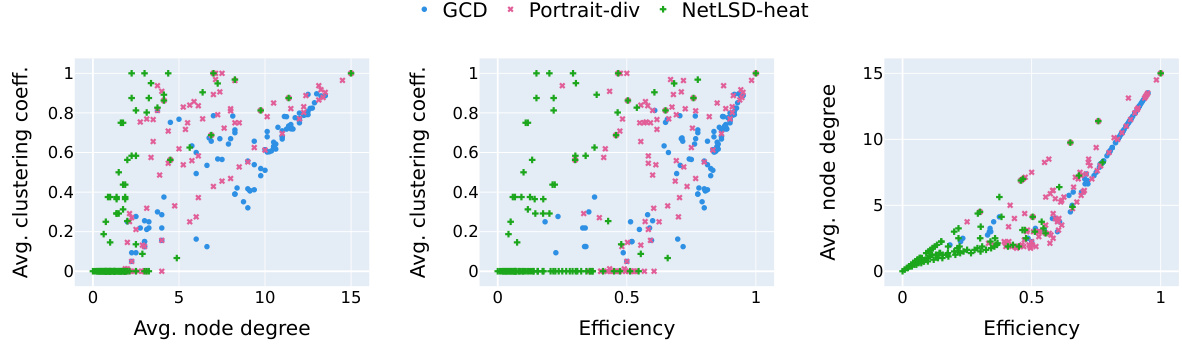
This figure visualizes the joint distributions of several pairs of graph characteristics for three different graph distance measures: GCD, Portrait Divergence, and NetLSD-heat. Each point represents a generated graph, with its x and y coordinates corresponding to the values of two graph characteristics (e.g., average node degree and average clustering coefficient). The different colors represent the different graph distance measures used to generate the graphs. The figure is intended to illustrate how different graph distances focus on different aspects of graph structure, leading to distinct sets of generated graphs with varying properties.
This figure shows a sample of structurally diverse graphs generated using the methods described in the paper. The graphs showcase a variety of structural properties, highlighting the diversity achieved by the proposed algorithms. These diverse graphs are useful for testing graph algorithms and evaluating neural approximations, as discussed in the paper.

This figure shows a sample of graphs generated by the algorithms proposed in the paper. The graphs illustrate the diversity achieved by the algorithms in terms of structure and topology. The different styles of graphs showcase various structural properties, highlighting the ability of the methods to generate a wide range of graph patterns, not limited to specific graph models.

This figure showcases a sample of 100 graphs generated using the Genetic algorithm with the Portrait Divergence graph distance. The graphs demonstrate the diversity achieved, with each exhibiting distinct structural properties. The variety in density, internal structure, cycle counts, and planarity highlight the success of the Genetic algorithm in producing structurally diverse graphs. The image provides a visual representation of graph diversity resulting from the combination of the Genetic algorithm and the specific graph distance metric used.

This figure shows a sample of graphs generated using the methods described in the paper. The graphs exhibit diverse structural properties, highlighting the success of the proposed methods in generating a structurally diverse set of graphs. The variety in graph density, connectivity, and overall structure demonstrates the algorithms’ ability to produce non-trivial graph topologies beyond those of simple random graph models.

This figure shows a sample of graphs generated by the proposed methods in the paper. It visually demonstrates the diversity of graph structures achieved, showcasing variations in density, connectivity patterns, presence of cycles, and overall topology. The graphs represent a small subset from a much larger set and serve to illustrate the effectiveness of the proposed approaches in creating structurally diverse graphs.

This figure shows a set of 100 graphs generated using the Genetic algorithm with the Portrait Divergence distance measure as the diversity metric. The graphs are visually diverse, showcasing a wide range of structural properties, including density, internal structure, number of cycles, and planarity. The diversity in graph structures demonstrates the effectiveness of the Genetic algorithm in producing representative samples from the graph space.

This figure visualizes the joint distribution of several pairs of graph characteristics, specifically for three different graph distance measures: Graphlet Correlation Distance (GCD), Portrait Divergence, and NetLSD-heat. Each subplot represents a pair of characteristics, such as average node degree vs. average clustering coefficient, average node degree vs. efficiency, and so on. The different colors represent different graph generation algorithms or baselines (ER-mix, GraphWorld, Greedy->Genetic->LocalOpt, and IGGM). The goal is to visually demonstrate how these algorithms produce graphs with differing structural properties across the various graph distance measures.
More on tables

This table presents the diversity measured by the Average metric for the same sets of graphs as in Table 1. It allows for a comparison of the diversity achieved using different graph generation algorithms and baselines, providing insights into the effectiveness of each approach in producing structurally diverse graphs. The values represent the average pairwise distances between graphs within each set.

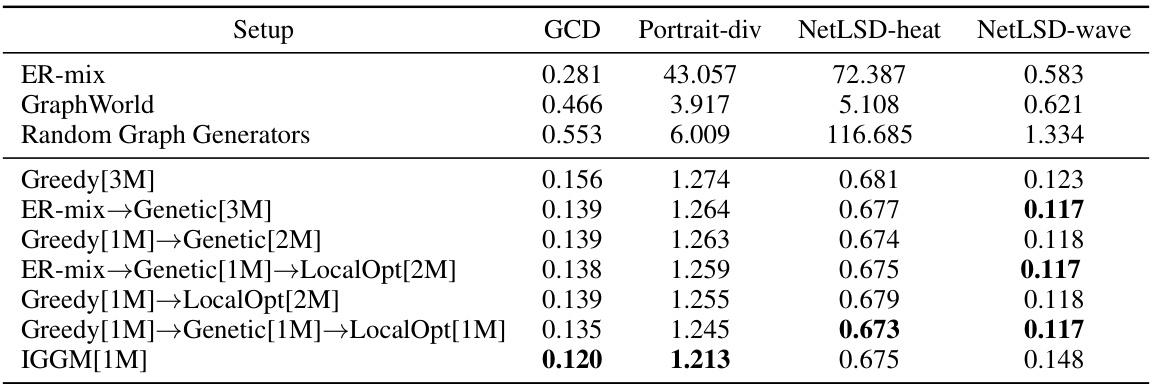
This table presents the results of energy optimization experiments for different graph generation methods. It compares the diversity of graphs generated by various methods, including Erdős-Rényi graphs, GraphWorld benchmark, and several proposed algorithms (Greedy, Genetic, LocalOpt, IGGM). Diversity is measured using the Energy measure with four different graph distances (GCD, Portrait-div, NetLSD-heat, NetLSD-wave). The table shows that the proposed methods significantly outperform the baseline methods in terms of diversity.

This table presents the results of energy optimization for different algorithms used to generate diverse graphs, specifically focusing on graphs with 16 nodes. The algorithms compared include various combinations of greedy, genetic, and local optimization approaches, along with baselines like Erdos-Renyi graphs and random graph generators. Four different graph distance measures are used: GCD, Portrait-div, NetLSD-heat, and NetLSD-wave, showing the energy optimization results for each. The table allows for a comparison of the effectiveness of different approaches in achieving high diversity, highlighting the impact of different distance measures and algorithm combinations.
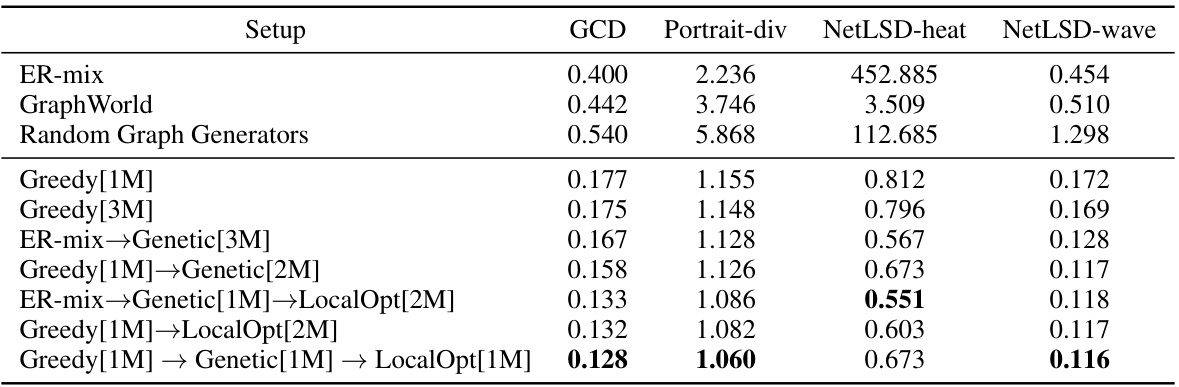
This table presents the results of energy optimization for graphs with 64 nodes using various algorithms. The table shows the energy scores obtained for different graph distance measures (GCD, Portrait-div, NetLSD-heat, NetLSD-wave) and algorithm combinations. The results are compared against baseline methods (ER-mix, GraphWorld, Random Graph Generators). Lower energy scores indicate better diversity. The table demonstrates the impact of different approaches on optimizing graph diversity, revealing the most effective strategies for generating structurally diverse graphs.
Full paper#