↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Continual learning, where models learn new tasks sequentially without forgetting previously learned tasks, is challenging when tasks are similar. This paper investigates how task similarity (in input features and output patterns) impacts continual learning performance. The authors highlight the issue of
catastrophic forgetting, where learning a new similar task can negatively impact performance on previous tasks. They also discuss the challenge of knowledge transfer, where similarity can help or hinder the transfer of knowledge from prior tasks to new ones.
To address these issues, the researchers developed a novel linear teacher-student model with latent structure to mathematically analyze the impact of task similarity on continual learning. They analytically evaluated the effects of three common continual learning techniques (task-dependent activity gating, plasticity gating, and weight regularization) on both knowledge transfer and retention, identifying optimal conditions for each technique’s effectiveness. The study’s key finding is that high input feature similarity with low output similarity is particularly detrimental, while the opposite scenario is relatively harmless. They propose improvements using adaptive gating and weight regularization within the Fisher information metric.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in continual learning because it provides analytical insights into how task similarity impacts model performance, especially the interplay between input feature and output similarity. It also offers practical guidance on mitigating catastrophic forgetting using task-dependent gating and weight regularization. This work is relevant to the ongoing effort to develop more robust and effective continual learning algorithms and could spur further research into the effects of task similarity and the development of more adaptive strategies.
Visual Insights#

Figure 1(A) shows a schematic of a continual linear regression model. The model uses a low-dimensional latent variable (s) to generate both inputs (x) and target outputs (y*). The student model learns a linear mapping (W) from the input to the output. Figure 1(B) is a phase diagram showing how knowledge transfer and retention depend on the feature (Pa) and readout (Pb) similarity between two tasks. Panels C and D illustrate continual learning scenarios with low feature similarity (permuted input pixels) and low readout similarity (permuted output labels) in the MNIST dataset, respectively. These examples correspond to the green and orange points on the phase diagram in panel B.
In-depth insights#
Task Similarity Impact#
The research paper investigates the multifaceted impact of task similarity on continual learning. Task similarity is shown to be a double-edged sword, presenting opportunities for positive knowledge transfer but also posing the risk of catastrophic forgetting and negative interference. The study reveals a complex interplay between the similarity of input features and output patterns. High input similarity coupled with low output similarity proves particularly detrimental, leading to poor knowledge transfer and retention. Conversely, low input and high output similarity scenarios are relatively benign. The analysis extends to the effects of various continual learning algorithms, including activity and plasticity gating, weight regularization, and their interaction with task similarity, revealing a non-monotonic relationship between similarity and algorithm effectiveness. Ultimately, the research provides a valuable framework for understanding when continual learning is difficult and offers potential mitigation strategies.
Continual Learning#
Continual learning, a subfield of machine learning, tackles the challenge of training AI models on sequential tasks without catastrophic forgetting of previously learned information. The core problem is that standard training methods overwrite previous knowledge, hindering performance on older tasks. This paper investigates how task similarity (in input features and output patterns) influences continual learning, revealing a critical interaction. High input similarity with low output similarity leads to catastrophic forgetting, while the opposite scenario is more benign. The authors demonstrate that task-dependent activity gating improves retention at the cost of transfer, while weight regularization based on the Fisher information metric significantly improves retention without sacrificing transfer. This work provides a valuable framework for understanding the challenges posed by task similarity in continual learning and offers insightful algorithmic solutions, offering potentially useful insights for improving the robustness and efficiency of AI systems in dynamic environments.
Gating & Regularization#
The effectiveness of gating and regularization techniques in continual learning is a key focus. The authors explore task-dependent activity gating, observing a trade-off between knowledge retention and transfer. High activity sparsity improves retention but hinders transfer, whereas dense activity proves more beneficial. Adaptive gating, dynamically adjusting activity levels based on performance, offers a potential solution to mitigate this trade-off. Furthermore, weight regularization, especially using the Fisher Information Metric, emerges as a powerful tool. Regularization in the Fisher Information Metric significantly enhances retention without compromising transfer, highlighting its superiority over Euclidean-based regularization. The analysis underscores the importance of task similarity: high input feature similarity coupled with low readout similarity proves particularly challenging for continual learning.
MNIST Experiment#
The MNIST experiment section would likely detail the application of the proposed continual learning methods to the classic MNIST handwritten digit dataset. It would likely involve a sequential learning paradigm, where the model is trained on a subset of MNIST digits (e.g., 0-4), then subsequently trained on a different, potentially overlapping subset (e.g., 5-9). The key performance metrics would be transfer learning, measuring the model’s ability to quickly learn new digits after initial training, and catastrophic forgetting, examining whether the model loses performance on previously learned digits. Task similarity, being a core concept, would be manipulated by varying the overlap between the digit subsets. The results would showcase the effectiveness of different continual learning algorithms (e.g., activity gating, weight regularization) in mitigating catastrophic forgetting and promoting efficient transfer learning across varying degrees of task similarity. The experiment would provide numerical validation of the theoretical findings, potentially showing how input/output feature similarity influences performance. Latent variable analysis may be incorporated to further understand the impact of data structure on continual learning, and the findings would be interpreted in the context of the theoretical framework provided earlier in the paper.
Future Directions#
Future research could explore extending the analytical framework beyond the linear teacher-student model to encompass more realistic neural network architectures, such as deep networks with non-linear activation functions. This would involve investigating how task similarity influences continual learning in these complex settings, potentially focusing on the role of hidden layer representations and interactions between different layers. Investigating the effect of different weight initialization strategies on continual learning performance would also be valuable, as this could shed light on how initial network configurations impact subsequent learning and forgetting. Furthermore, exploring different types of task similarity beyond feature and readout similarity is crucial. This could encompass analysing tasks with similar input but different outputs, or tasks with similar outputs but dissimilar inputs. Developing more robust and efficient algorithms for continual learning that adapt to varying levels of task similarity is another important direction. Finally, applying the theoretical framework developed to other continual learning challenges, such as learning in non-stationary environments or handling class-incremental learning tasks, would expand the scope and impact of this research.
More visual insights#
More on figures

This figure displays results from a vanilla model (no gating or regularization) of continual learning performance. Panel A shows the calculation of transfer and retention error, while panels B and C show how transfer performance varies with feature similarity (ρa) and readout similarity (ρb). Panels D-G show how retention performance varies with ρa and ρb, with panel G magnifying a specific region of panel E to highlight local minima/maxima.
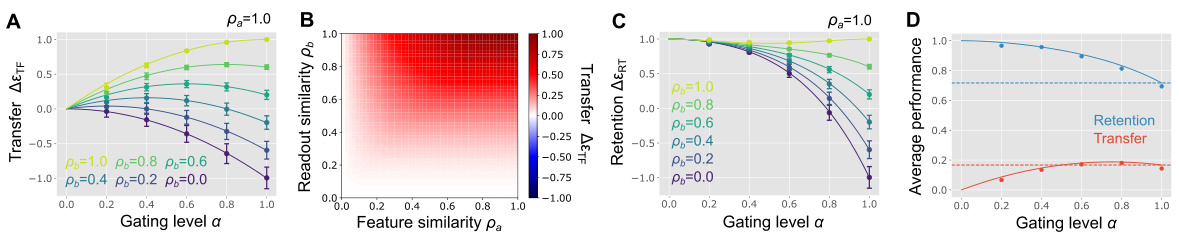
This figure shows the results of a random task-dependent activity gating model. It shows how the transfer and retention performance change depending on different parameters such as feature similarity, readout similarity, and gating level. The results are shown in four different subplots to illustrate how each parameter affects the performance. The results are obtained through numerical estimations, and horizontal dashed lines are added to compare the results against the baseline performance.
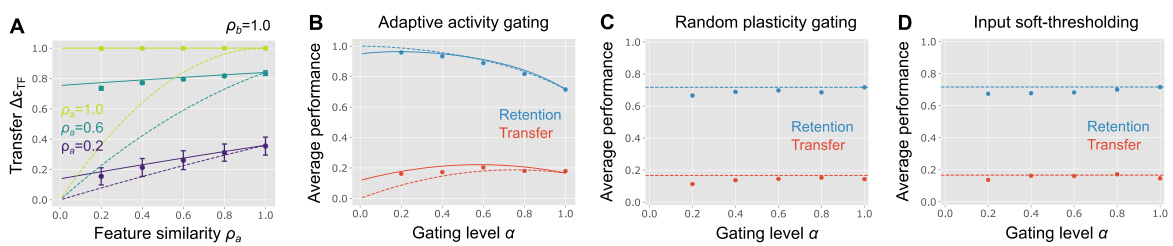
Figure 3 presents the results of simulations using a random task-dependent activity gating model. The results are shown as a function of the gating level (α), which is defined as the proportion of active input neurons. Panel (A) shows the transfer performance when input feature similarity (ρa) is 1.0. Panel (B) shows the transfer performance under the optimal gating level, with the optimal level determined by maximizing transfer performance. Panel (C) shows the retention performance when ρa = 1.0, and Panel (D) displays the average transfer and retention performances across a uniform distribution of task similarities (0 ≤ ρa, ρb ≤ 1). The performance of the vanilla model without gating is shown as a horizontal dashed line in each panel for comparison.
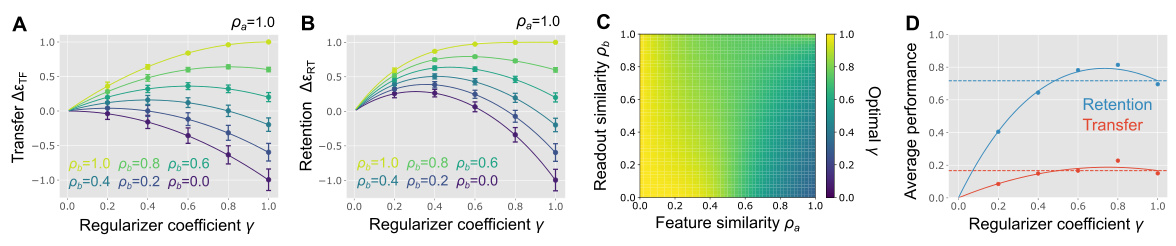
This figure shows the results of using weight regularization in a Euclidean metric for continual learning. Panels A and B illustrate the transfer and retention performance, respectively, as a function of the regularizer coefficient (γ) and task similarity (ρa and ρb). Panel C displays the optimal regularizer coefficient (γ) that maximizes retention performance for various levels of task similarity. Finally, Panel D presents the average performance (both transfer and retention) across a range of task similarities.
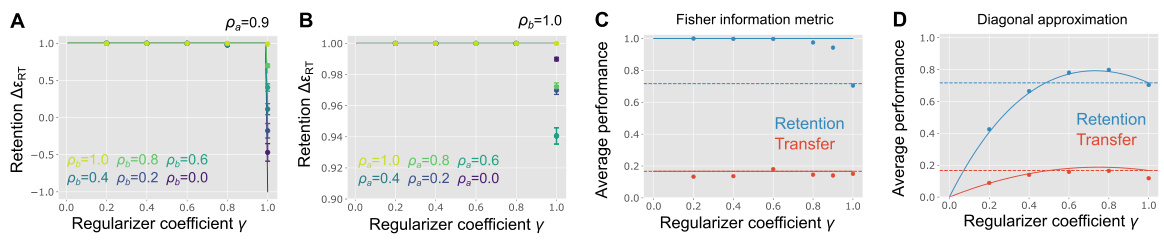
This figure shows the results of applying weight regularization using the Fisher information metric and its diagonal approximation. Panels A and B illustrate how retention performance varies with the regularizer coefficient (gamma) and different levels of task similarity (feature and readout). Panels C and D present the average transfer and retention performance across various task similarity conditions for both the exact Fisher information metric and its diagonal approximation. The diagonal approximation is shown to be less robust against task similarity.
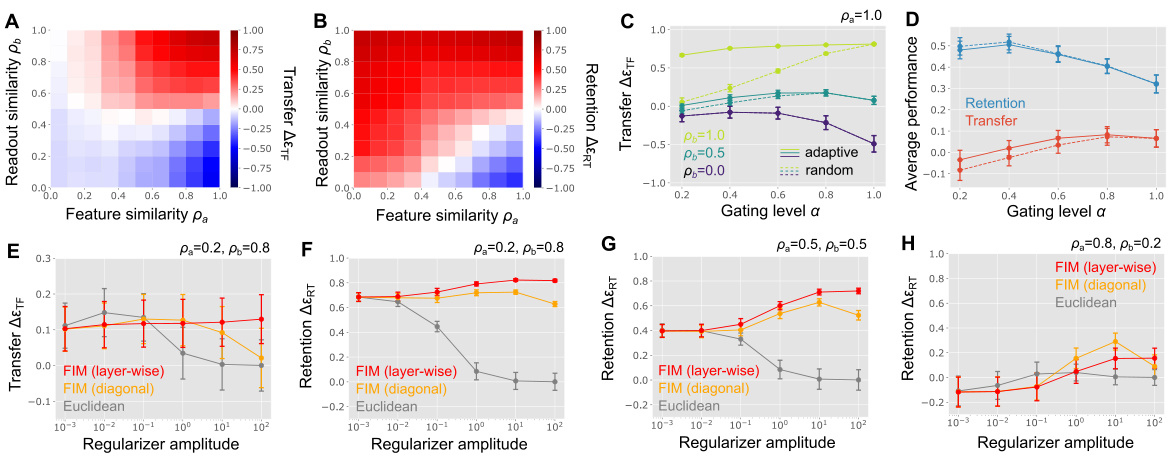
This figure shows the results of numerical experiments using a permuted MNIST dataset with a latent structure. Panels A and B display the transfer and retention performance of a vanilla model, demonstrating the asymmetric and non-monotonic relationship between task similarity and performance. Panels C and D illustrate the impact of random and adaptive activity gating on transfer and retention, highlighting how adaptive gating can mitigate the tradeoff between these two objectives. Finally, panels E through H compare the performance of weight regularization using different metrics (Euclidean, Fisher information, diagonal approximation of Fisher information, layer-wise approximation of Fisher information), showcasing that the layer-wise approximation of the Fisher information metric achieves the best retention performance.

This figure examines how the gating level affects the trade-off between transfer and retention performance in continual learning. Panel A shows a phase diagram illustrating the different regions of gating level behavior as a function of feature and readout similarity. Panels B-D then delve deeper into specific regions of this phase diagram, showing the transfer and retention performance curves for different gating levels within those regions. The results demonstrate the complex interplay between gating, feature similarity, and readout similarity in determining continual learning success.

Figure 9 shows the results of weight regularization in Euclidean metric. Panels A and B illustrate how the optimal regularizer coefficient γ that maximizes transfer performance and the resulting performance vary depending on feature similarity (ρa) and readout similarity (ρb). Panels C and D show the optimal regularizer coefficient γ for retention performance and the resulting performance under different combinations of feature and readout similarity. Note that panel C is the same as Figure 5C.
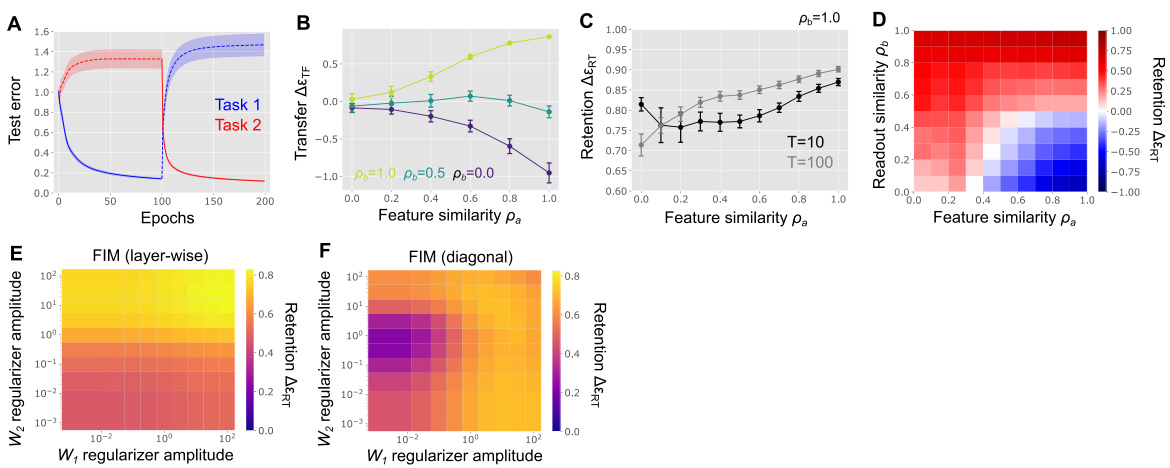
This figure shows the results of experiments on a permuted MNIST dataset with latent variables. It demonstrates the transfer and retention performance for several continual learning algorithms, including a vanilla model, random and adaptive activity gating, and weight regularization using different metrics (Euclidean, Fisher information matrix, layer-wise and diagonal approximations). The plots illustrate how performance varies based on task similarity (feature and readout), highlighting the effects of different continual learning strategies. Error bars represent standard error.

This figure shows the results of experiments conducted on a permuted MNIST dataset with latent variables. The experiments test the impact of task similarity and different continual learning algorithms on transfer and retention performance. Panel A and B illustrate the baseline transfer and retention for a vanilla model. Panels C and D show results using random and adaptive activity gating. Panels E-H present results for weight regularization using three different methods: Euclidean metric, Fisher information metric (layer-wise approximation), and Fisher information metric (diagonal approximation). The graphs display transfer and retention performance as a function of task similarity (feature and readout similarity) and regularization strength.
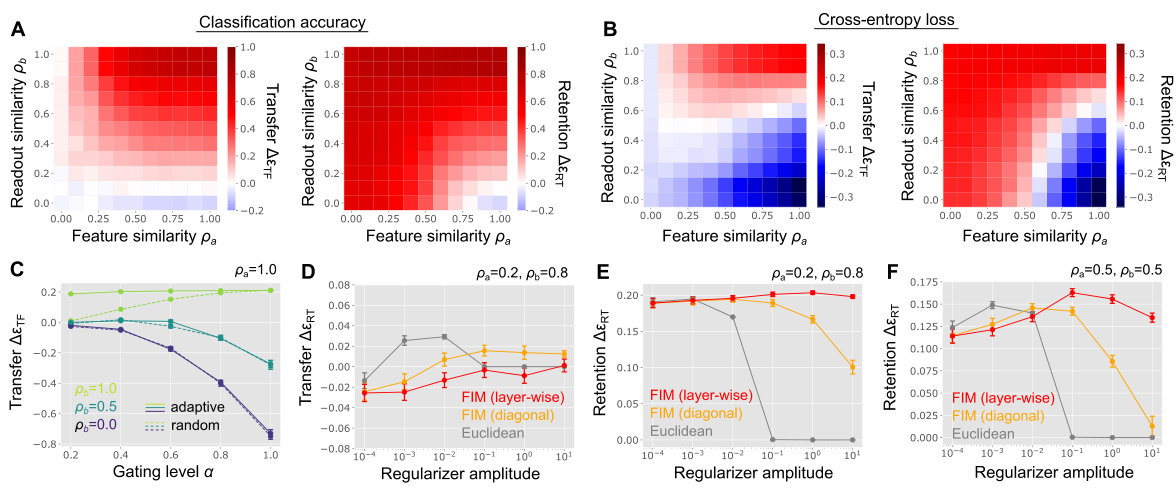
This figure shows the results of experiments on the permuted MNIST dataset where both input pixels and output labels were permuted to control feature and readout similarity. Panels A and B show the transfer and classification performance using classification accuracy and cross-entropy loss, respectively, as performance metrics. Panel C compares transfer performance using random versus adaptive activity gating. Panels D-F illustrate the effect of weight regularization using different metrics (Euclidean, Fisher information matrix (FIM) with diagonal and layer-wise approximations) on transfer and retention performance under varying levels of feature and readout similarity.
Full paper#



















