↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current large-scale AI model training often relies on third-party services, raising concerns about the training process’s integrity and potential for attacks like data poisoning. Existing verifiable training methods face challenges in scalability and robustness due to the nondeterministic nature of GPU hardware. Nondeterminism leads to different results when the same training process runs on different GPU types, hindering the verification process.
This research proposes a novel approach to address this challenge. By training models at a higher precision than needed, and carefully recording and sharing rounding decisions based on an adaptive thresholding technique, the researchers were able to achieve exact replication of the training process across different GPUs. This significantly reduces the storage and time overhead associated with verifiable training methods, making it scalable for large models. The method leverages an interactive verification game to ensure accountability and allows for efficient dispute resolution.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in verifiable machine learning and distributed computing. It offers a practical solution to the problem of nondeterminism in GPU-based training, a significant hurdle in verifying the correctness of AI model training across various hardware platforms. The work opens new avenues for secure and reliable outsourced training, addressing a critical trust issue in the increasingly popular model-as-a-service paradigm.
Visual Insights#
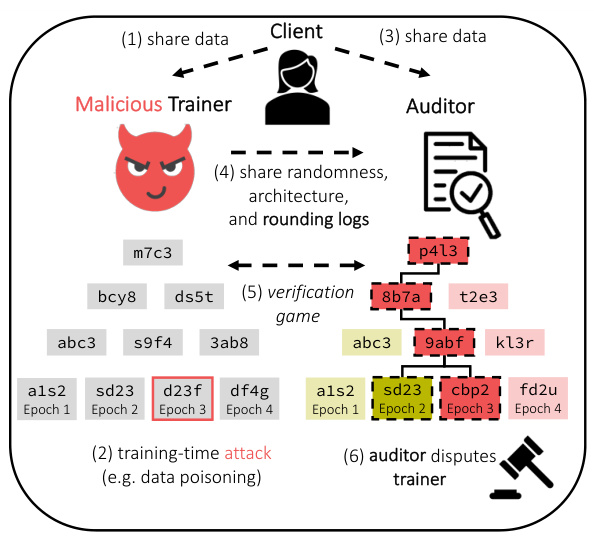
This figure illustrates the optimistic verifiable training scheme proposed in the paper. A malicious trainer trains a model for a client, potentially introducing a training-time attack (e.g., data poisoning). An auditor can then challenge the trainer by replicating the training process using their own resources. To ensure correctness, model weights are stored in a Merkle tree, allowing for efficient verification. A binary search game is used to pinpoint any discrepancies. The scheme addresses the challenge of GPU nondeterminism, making verification robust across different GPU architectures.

This table shows two examples to demonstrate how floating point accumulation errors can occur when rounding from higher precision (FP32) to lower precision (FP16). In the first example, the same result is obtained regardless of the order of summation because the error introduced by rounding is less than the least significant bit of the FP16 representation. However, in the second example, the accumulation order affects the final rounded FP16 result, illustrating non-determinism due to floating point arithmetic.
In-depth insights#
Verifiable Training#
Verifiable training tackles the crucial problem of ensuring the integrity of AI model training, especially in outsourced scenarios. Trust becomes a major concern when clients lack the resources to train models themselves and must rely on third-party services. Existing methods, like proof-based systems, face scalability challenges, while optimistic approaches relying on auditor replication struggle with hardware nondeterminism, leading to unreliable verification. This research proposes a novel approach that cleverly mitigates nondeterminism by combining high-precision training with controlled rounding and adaptive thresholding. This allows for exact training replication across different GPU architectures, demonstrating the efficacy of the approach for large models. The approach significantly improves upon existing methods regarding storage and time efficiency. The resulting verifiable training scheme offers a practical solution for clients to verify the correctness of their model training, fostering accountability and trust in outsourced AI services.
GPU Nondeterminism#
The section on “GPU Nondeterminism” highlights a critical challenge in verifiable machine learning. Nondeterministic behavior in GPUs, arising from factors like floating-point arithmetic, parallel computation, and memory hierarchy variations, prevents exact replication of training processes across different GPU architectures. This makes it difficult to verify if a model was trained correctly by a third-party service provider, as an auditor’s replicated training may diverge from the original. The authors underscore the significance of addressing this, as nondeterministic training can lead to issues like reproducibility concerns, and potentially bias and inconsistent model performance. The core issue is the difficulty of achieving bit-wise identical results across GPUs, even with identical code and seeds. The paper’s innovative solution directly tackles this challenge by introducing novel techniques to control nondeterminism during training, paving the way for reliable and trustworthy verifiable training systems.
Adaptive Threshold#
The adaptive threshold technique is a crucial element in this verifiable training method. It directly addresses the challenge of nondeterminism in floating-point computations across different GPUs by intelligently deciding when to log rounding decisions. Instead of always recording the rounding direction, which would lead to excessive storage costs, the adaptive threshold determines whether the divergence between GPU computations is significant enough to warrant logging. This dynamic approach reduces the amount of data that needs to be shared between the trainer and auditor, resulting in significant storage savings. The algorithm cleverly balances the accuracy of verifiable training with the efficiency of storage, thus making the overall method more scalable and practical for larger models.
Storage Efficiency#
The research paper explores storage efficiency in verifiable training by addressing the challenge of large storage costs associated with logging rounding decisions. Efficient encoding techniques, reducing storage needs by 77%, are implemented by packing log entries. An adaptive thresholding mechanism further reduces storage by intelligently selecting which rounding decisions need logging, further improving efficiency. The method is compared with other verifiable training approaches, demonstrating significant storage cost reductions compared to proof-based systems. These strategies are vital for scaling verifiable training to larger models and datasets where storage costs can be prohibitive. The overall efficiency gains highlight the practicality of the proposed optimistic verifiable training approach.
Future Directions#
Future research could explore distributed verifiable training, adapting the proposed methods to handle the complexities of parallel computation across multiple machines. Another key area is improving the efficiency of the logging mechanism, potentially by developing more sophisticated techniques to predict and selectively log rounding decisions only when necessary, thereby reducing the storage overhead. Investigating alternative rounding strategies beyond simple rounding to the nearest value could also enhance the robustness and accuracy of the approach. Finally, extending the framework to support a wider range of model architectures and training tasks would broaden its applicability and impact within the machine learning community. A formal security analysis to rigorously prove the security guarantees under various attack models would also bolster the trustworthiness of the system.
More visual insights#
More on figures
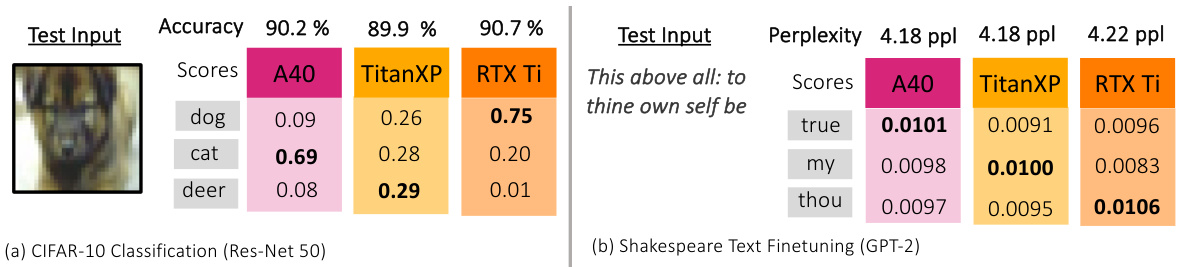
This figure shows the results of training the same model (ResNet-50 for image classification and GPT-2 for text generation) on three different NVIDIA GPUs (A40, Titan XP, and RTX 2080 Ti) using the same software version, random seed, and deterministic algorithms. Despite these measures, significant differences in the model’s outputs are observed, as indicated by the varying accuracy and perplexity scores for the same inputs. This demonstrates that nondeterminism persists even under controlled conditions.
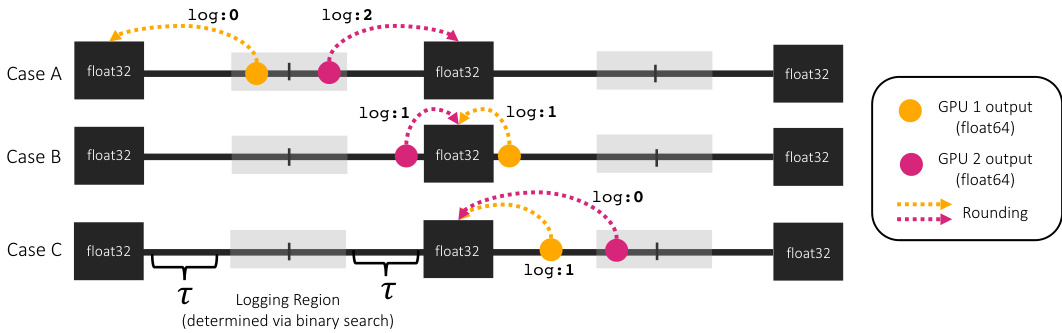
This figure illustrates how nondeterminism in floating-point arithmetic across different GPUs can lead to different rounding results, even when starting with the same high-precision input. It introduces the concept of a ’logging region’ and a threshold (τ) to control when rounding decisions are recorded and shared between the trainer and auditor to maintain consistency. The three cases (A, B, C) show different scenarios and how the threshold affects the logging strategy.
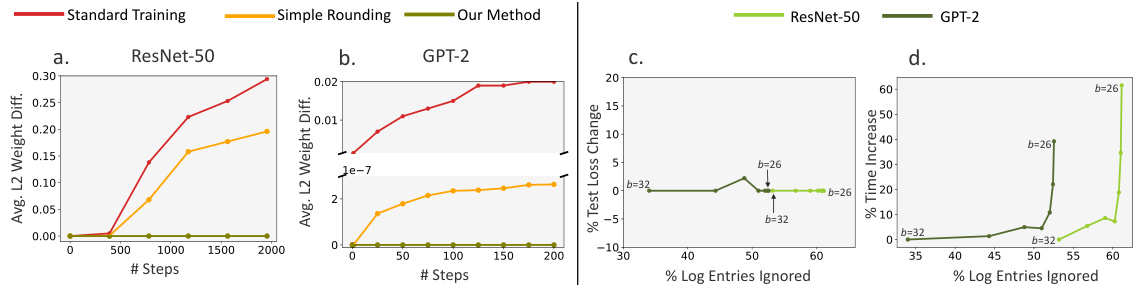
This figure shows the results of applying different training methods to ResNet-50 and GPT-2 models on different GPUs. (a) and (b) demonstrate that the proposed method successfully prevents model divergence caused by hardware nondeterminism, unlike standard training and simple rounding. (c) and (d) analyze the trade-off between rounding strength and performance, showing that stronger rounding improves determinism but increases training time.
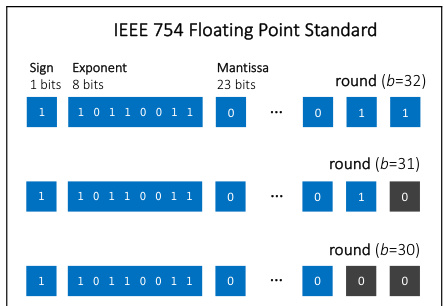
This figure illustrates how rounding to a certain number of bits (b) in floating-point representation works. It shows that rounding to b bits means selecting the nearest 32-bit floating-point number with zeros in the least significant 32-b bits of the mantissa. The exponent part of the number remains unchanged by the rounding operation. This process is crucial for controlling non-determinism in the training process, as it ensures that even with different GPUs, rounding will produce the same value when the intermediate computations are performed with higher precision.
More on tables

This table compares the storage costs of the proposed verifiable training method with different encoding schemes and rounding amounts (b). It highlights the significant reduction in storage costs achieved by efficient encoding and aggressive rounding compared to a naive approach and a previous method (Jia et al., 2021), demonstrating the scalability and efficiency of the proposed approach.

This table shows the average number of rounding corrections the auditor needs to perform per training step for different rounding amounts (b) in both the forward and backward passes of ResNet-50 and GPT-2 models. The results demonstrate that even with a high-precision rounding (b=32), the number of corrections required is extremely low (less than 0.01% of samples), highlighting the efficiency of the proposed verifiable training method.

This table shows the adaptive thresholds (τ) determined by Algorithm 3 for different layer types in neural networks (2D Convolution, Batch Norm, Linear, Layer Norm). The threshold is crucial for efficiently controlling nondeterminism during training by selectively logging rounding decisions. The dimensions shown represent the input/output shapes for each layer.

This table shows the training time requirements for both the trainer and auditor for one step of training for ResNet-50 and GPT-2. The time is broken down into the original time without any rounding or disk I/O, the trainer time and the auditor time. The relative increase in time for both trainer and auditor is more important than the absolute time.

This table compares the model divergence caused by data ordering and GPU non-determinism. The metrics used are the L2 weight difference (the Euclidean distance between the model weights) and the L2 output distance (the difference in model outputs). The results show that data ordering has a much greater impact on model divergence than GPU non-determinism.
Full paper#



















