↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Large Language Models (LLMs) are powerful tools for reasoning, but their application to complex combinatorial problems (CPs) remains limited. Existing prompting techniques often fall short when dealing with the inherent complexity and NP-hard nature of these problems. This leads to inadequate solutions, especially for larger problem instances. This necessitates the development of more robust and effective prompting strategies to fully utilize LLMs’ potential in solving CPs.
This research introduces a novel prompting strategy called Self-Guiding Exploration (SGE) to improve the performance of LLMs on CPs. SGE autonomously generates multiple solution trajectories, breaks them down into subtasks, executes them sequentially, and refines results for optimal outcomes. It significantly outperforms existing strategies, showcasing its effectiveness across diverse CPs and achieving higher accuracy than the best-existing results in other reasoning tasks. This demonstrates the potential of SGE as a versatile metaheuristic for tackling combinatorial challenges, highlighting its applicability and effectiveness across various domains.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with LLMs and combinatorial problems. It demonstrates the effectiveness of LLMs in solving complex optimization tasks, a field previously considered beyond their capabilities. The proposed method, Self-Guiding Exploration (SGE), offers a new approach to prompting LLMs that significantly improves performance, opening up avenues for future research in this area and across diverse reasoning tasks.
Visual Insights#
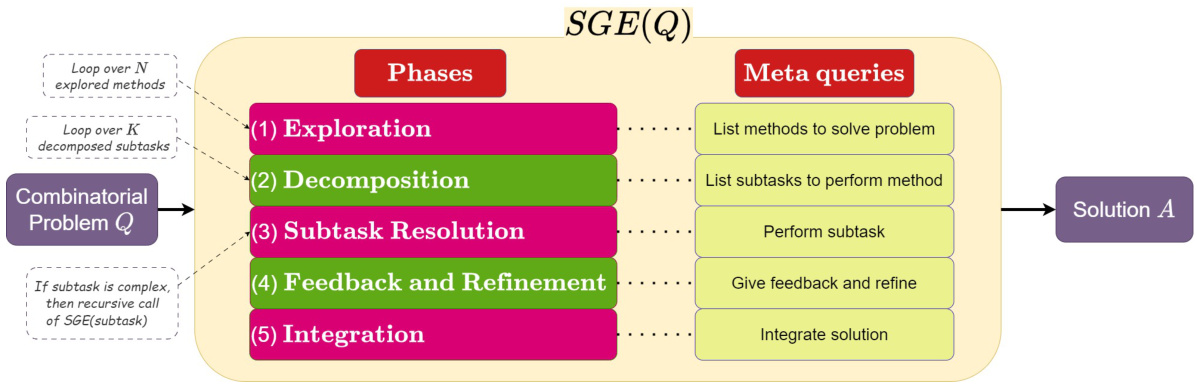
This figure illustrates the Self-Guiding Exploration (SGE) algorithm’s workflow. The algorithm processes a combinatorial problem (Q) through five phases: exploration (generating multiple solution trajectories), decomposition (breaking trajectories into subtasks), subtask resolution (executing subtasks), feedback and refinement (improving results), and integration (combining results into a final solution, A). The key feature is the algorithm’s autonomous operation, eliminating the need for task-specific prompts.

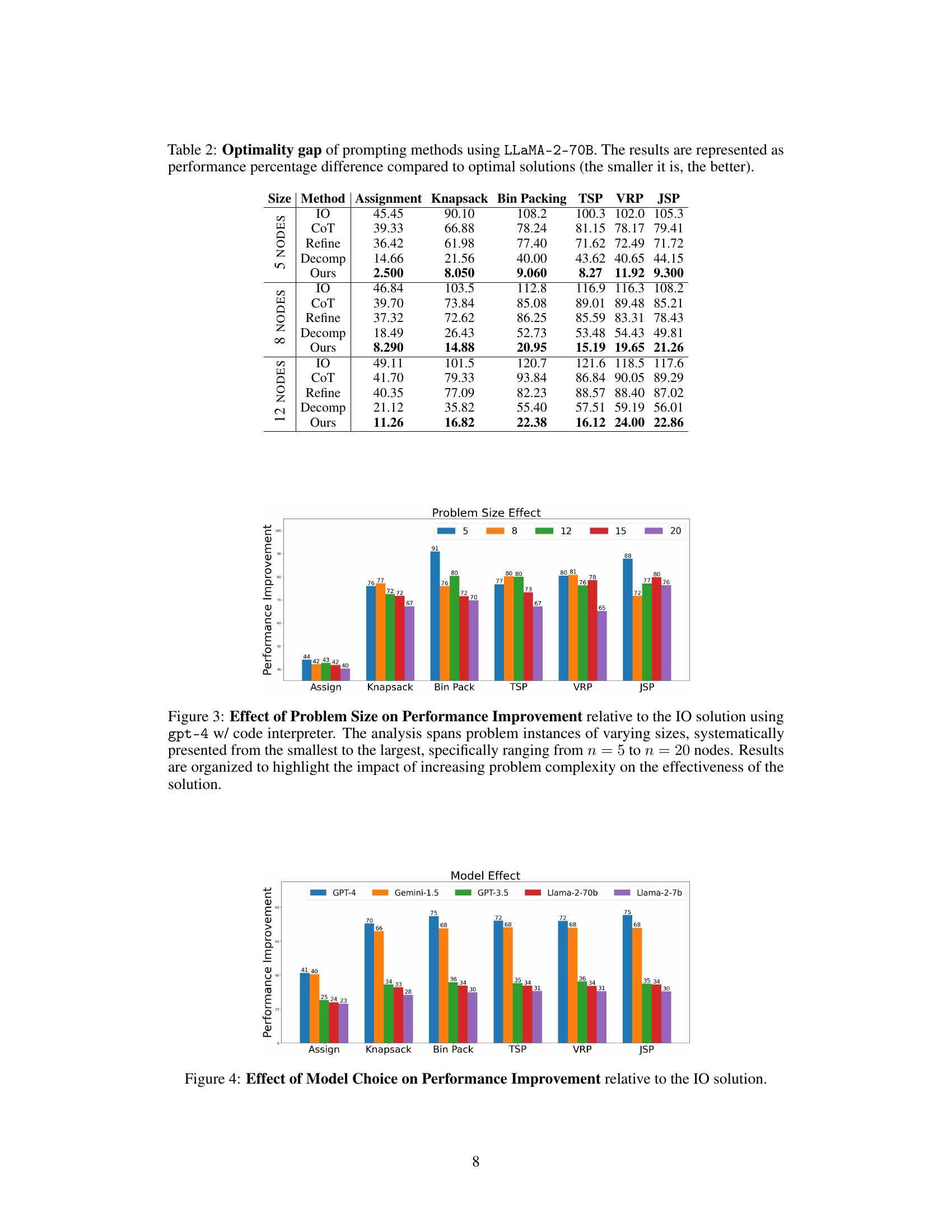
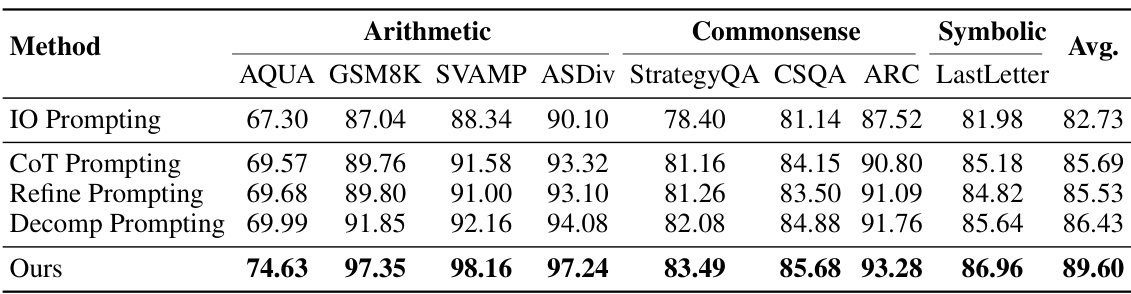
This table presents the performance improvement of the proposed Self-Guiding Exploration (SGE) method compared to several baseline methods (Input-Output (IO), Chain-of-Thought (CoT), Self-Refine, and Decomposition) for six different combinatorial problems (CPs) using two large language models (LLMs): GPT-4 and Gemini-1.5. The improvement is calculated as a percentage reduction in the cost of the solution found by each method compared to the IO baseline. Higher percentages indicate better performance. The number of candidates for the CoT method is set equal to the number of thought trajectories generated by SGE.
In-depth insights#
LLM for CPs#
The application of Large Language Models (LLMs) to Combinatorial Problems (CPs) is a relatively unexplored area despite LLMs’ success in other reasoning tasks. This is mainly due to the inherent complexity of CPs, which are often NP-hard and require sophisticated solution strategies. Existing LLMs struggle with the scale and complexity of many real-world CPs. This paper explores a new prompting strategy, Self-Guiding Exploration (SGE), to address this challenge. SGE enhances LLM performance by autonomously generating multiple solution trajectories, breaking them into manageable subtasks, and iteratively refining results. The approach shows significant improvement over existing methods across diverse CPs like the Travelling Salesman Problem and Job Scheduling, demonstrating the potential of LLMs for solving a wider range of complex optimization problems. Further research should explore how to improve efficiency and address limitations. The effectiveness of SGE also highlights the value of investigating various prompting techniques for LLMs applied to computationally complex domains.
SGE Prompting#
Self-Guiding Exploration (SGE) prompting presents a novel approach to solving combinatorial problems (CPs) using Large Language Models (LLMs). Instead of relying on pre-defined heuristics or task-specific prompts, SGE leverages the LLM’s capacity for autonomous exploration and decomposition. The method generates multiple solution trajectories, each representing a different heuristic strategy, and then breaks down these trajectories into smaller, manageable subtasks. This decomposition allows the LLM to tackle complex heuristics step-by-step, improving accuracy and performance. A key advantage of SGE is its adaptability; it uses general-purpose prompts, making it applicable to a wide range of CPs without requiring task-specific modifications. The iterative refinement process inherent in SGE further enhances the quality of the final solution. Empirical results demonstrate significant performance gains over existing prompting strategies across diverse combinatorial tasks and various reasoning benchmarks, highlighting SGE’s effectiveness and versatility. The research suggests SGE is a promising technique for broadening LLMs’ capabilities in handling complex optimization challenges.
CP Experiments#
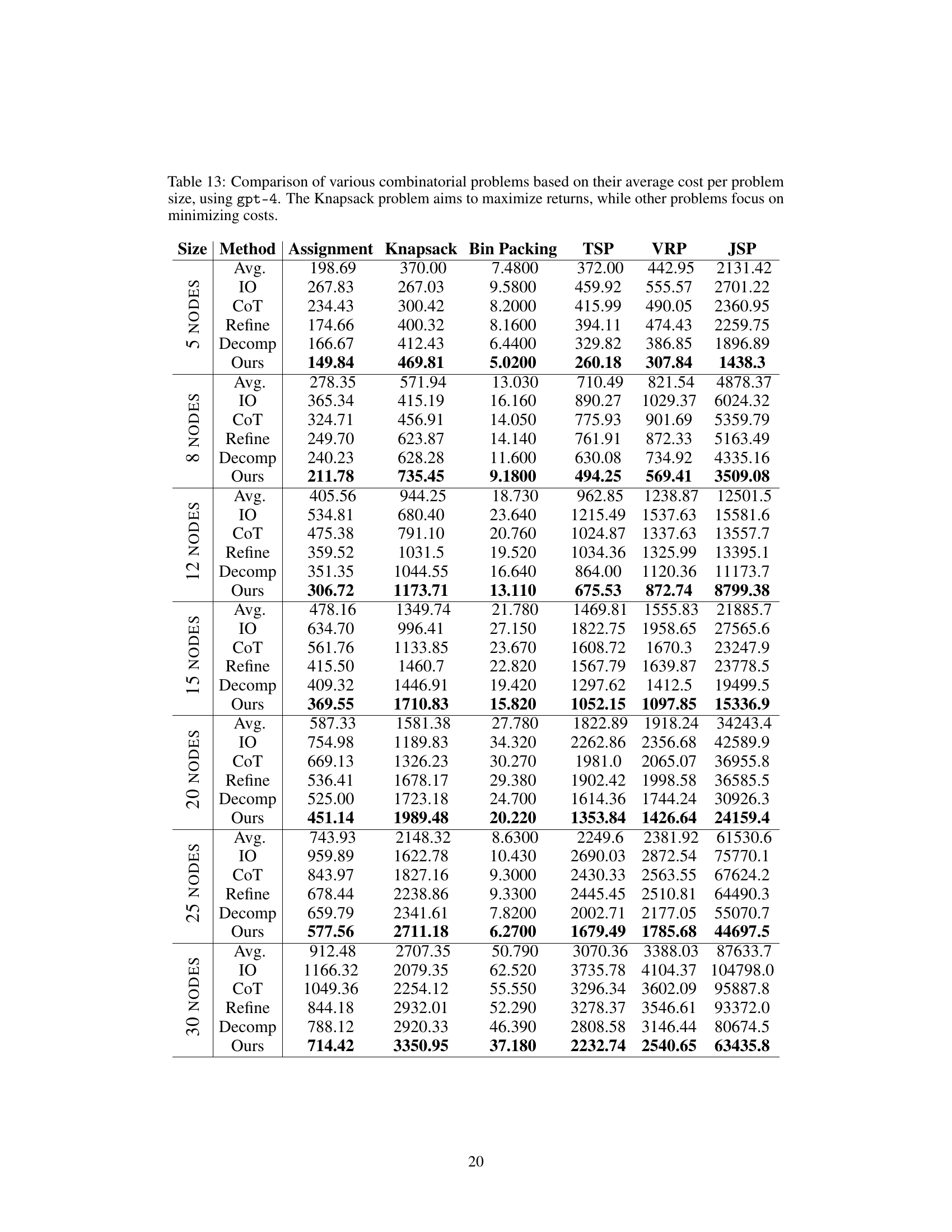
The CP (Combinatorial Problem) experiments section of the research paper would likely detail the methodology and results of applying the proposed Self-Guiding Exploration (SGE) method to various CP instances. This would involve a description of the chosen CPs, including their specific characteristics and complexity. Problem size variations would be crucial, testing the scalability of SGE against established baselines. Key performance metrics such as solution quality (optimality gap from known optimal solutions or comparison against the best known solution) and computational efficiency (time and resource usage) would be rigorously measured and compared. The experimental setup would likely encompass multiple runs for each instance to account for stochasticity and provide statistical validity. Finally, the results would showcase SGE’s performance, highlighting its strengths and limitations relative to the baselines across different CPs and problem sizes, likely with statistical significance testing to support the claims.
SGE Scalability#
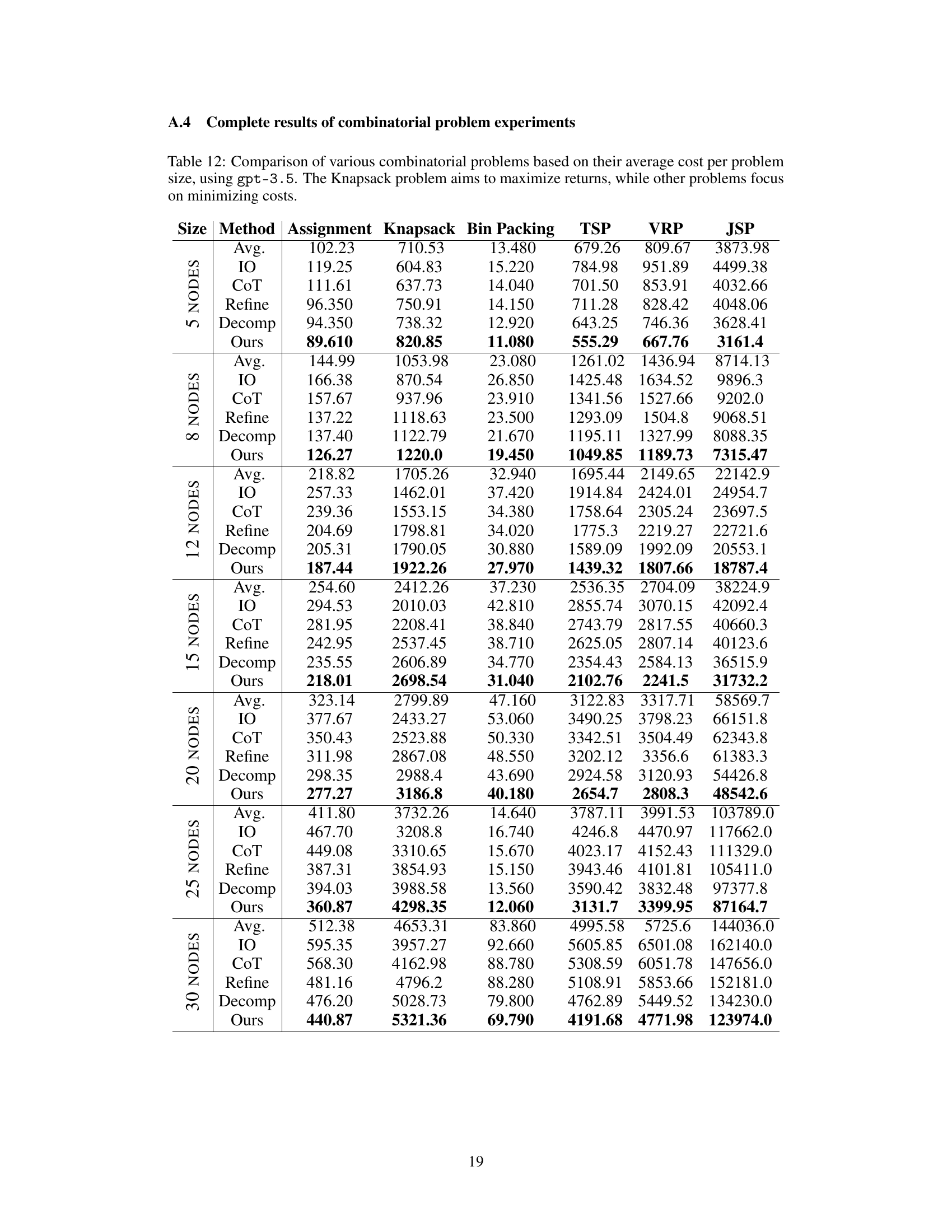
The scalability of the Self-Guiding Exploration (SGE) method for solving combinatorial problems is a crucial aspect to consider. While SGE demonstrates promising results on smaller problem instances, its ability to handle larger, more complex problems needs further investigation. The computational cost of SGE increases significantly with problem size, as it involves generating multiple thought trajectories and decomposing them into subtasks. This suggests potential limitations in applying SGE to real-world scenarios where massive-scale combinatorial problems are prevalent. Further research should explore optimization strategies to mitigate the computational burden, such as refining the trajectory generation process or employing more efficient subtask decomposition techniques. Investigating the impact of different LLM models on SGE’s scalability is also important, as LLMs with greater capacity and specialized capabilities might offer better performance on larger problems. Ultimately, assessing SGE’s scalability relative to existing methods such as Google OR-Tools and traditional heuristics provides valuable insights into its practical applicability and potential for broader deployment.
Future of LLMs#
The future of LLMs is bright, but also uncertain. Continued advancements in model scaling will likely lead to even more powerful and versatile models capable of handling increasingly complex tasks. However, challenges remain in areas such as efficiency, bias mitigation, and explainability. Future research should focus on developing more efficient training methods, addressing biases inherent in training data, and making LLM decision-making processes more transparent and understandable. Furthermore, the integration of LLMs with other technologies, such as robotics and computer vision, holds tremendous potential for creating truly intelligent systems that can interact with and understand the real world in sophisticated ways. Ethical considerations, including the potential for misuse and the need for responsible development and deployment, must be central to this process. Ultimately, the future of LLMs hinges on striking a balance between innovation and responsible development, ensuring these powerful tools are used to benefit society as a whole.
More visual insights#
More on figures

This figure illustrates the Self-Guiding Exploration (SGE) method’s five phases: exploration, decomposition, subtask resolution, feedback and refinement, and integration. It shows how the model autonomously generates multiple solution trajectories, breaks them down into subtasks, solves them, refines the results based on feedback, and combines everything into a final solution. The key is that it’s fully autonomous, unlike many other methods that rely on task-specific prompts or manual intervention.
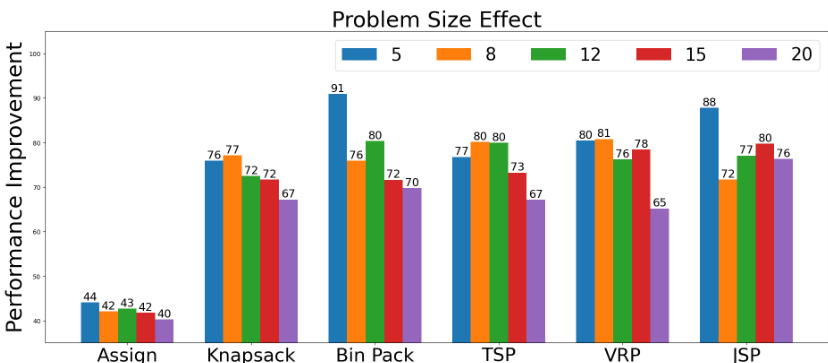
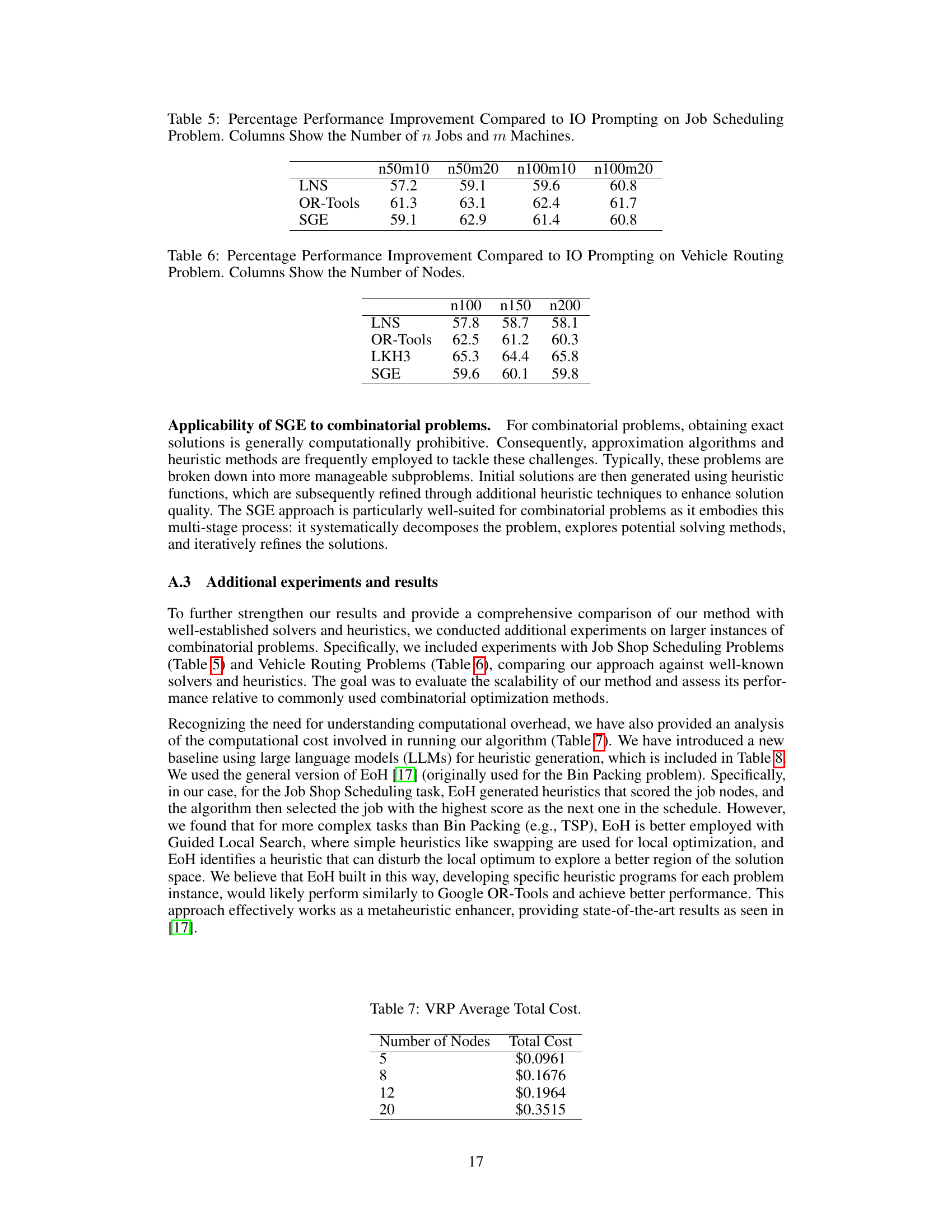
The bar chart visualizes the performance improvement of the Self-Guiding Exploration (SGE) method compared to the Input-Output (IO) baseline across six combinatorial problems (Assignment, Knapsack, Bin Packing, TSP, VRP, JSP) with varying problem sizes (5, 8, 12, 15, 20 nodes). The chart demonstrates how the performance improvement of SGE diminishes with increasing problem size, suggesting that the complexity of larger instances presents greater challenges for the model.

This bar chart visualizes the performance improvement of Self-Guiding Exploration (SGE) across different Large Language Models (LLMs) for six combinatorial tasks (Assignment, Knapsack, Bin Packing, TSP, VRP, JSP). Each bar represents a task, and the height indicates the percentage improvement in performance achieved by SGE compared to the baseline Input-Output (IO) method for that task, broken down by LLM used. The chart helps to assess how the choice of the LLM affects the efficacy of SGE in solving combinatorial problems.
More on tables
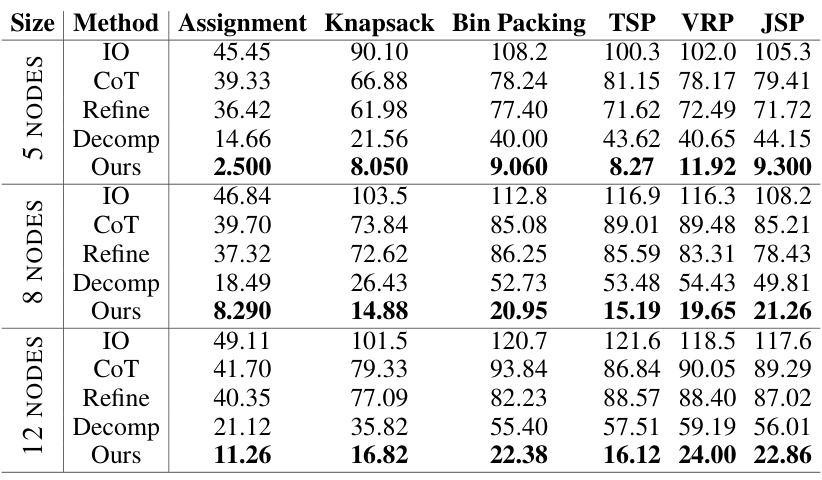
This table presents the percentage improvement in cost achieved by the Self-Guiding Exploration (SGE) method compared to four baseline methods (Input-Output, Chain-of-Thought, Self-Refine, and Decomposition) across six different combinatorial problems (Assignment, Knapsack, Bin Packing, Traveling Salesman, Vehicle Routing, Job Scheduling) using two different large language models (GPT-4 and Gemini-1.5). Higher percentages indicate better performance.
This table presents the performance improvement achieved by the Self-Guiding Exploration (SGE) method compared to four baseline methods (Input-Output (IO), Chain-of-Thought (CoT), Self-Refine (Refine), and Decomposition) across six combinatorial problems (Assignment, Knapsack, Bin Packing, Traveling Salesman, Vehicle Routing, and Job Scheduling). The results are shown for two large language models (GPT-4 and Gemini-1.5). The improvement is calculated as the percentage decrease in cost compared to the IO baseline. The table highlights that SGE outperforms the other methods significantly, with the improvement increasing as the complexity of the problem increases.
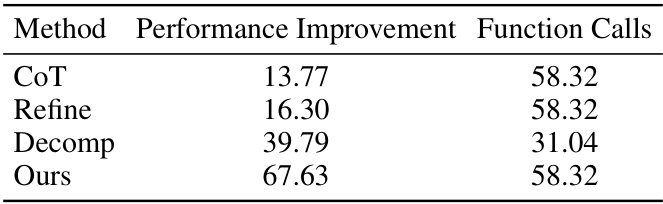
This table presents the performance improvement of the proposed Self-Guiding Exploration (SGE) method and three baseline methods (CoT, Refine, Decomp) compared to a basic Input-Output (IO) approach on six combinatorial problems (CPs) using two large language models (LLMs): GPT-4 and Gemini-1.5. The improvement is measured as a percentage reduction in cost compared to the IO baseline. The table shows that SGE significantly outperforms the baseline methods across all tasks and models.

This table presents the percentage improvement in performance achieved by the Self-Guiding Exploration (SGE) method compared to four baseline methods (Input-Output, Chain-of-Thought, Self-Refine, and Decomposition) across six combinatorial problem tasks (Assignment, Knapsack, Bin Packing, Traveling Salesman, Vehicle Routing, and Job Scheduling) using two different Large Language Models (GPT-4 and Gemini-1.5). The improvement is calculated as a percentage relative to the Input-Output baseline’s cost. Higher values indicate better performance.

This table presents the performance improvement of different methods compared to the basic Input-Output (IO) prompting method for solving Vehicle Routing Problems (VRPs). The improvement is shown as a percentage for various problem sizes (number of nodes). Methods compared include LNS (Large Neighborhood Search), Google OR-Tools, LKH3 (Lin-Kernighan Heuristic), and the proposed SGE (Self-Guiding Exploration) method. Larger percentage values indicate better performance.
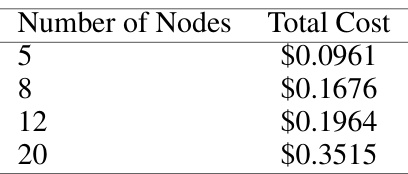
This table shows the average total cost for solving the Vehicle Routing Problem (VRP) using the Self-Guiding Exploration (SGE) method, categorized by the number of nodes (cities). The costs reflect the computational expense incurred when utilizing a large language model to solve the VRP using the described method. A higher number of nodes generally correlates with a higher total cost.

This table presents the percentage improvement in performance achieved by different methods (LNS, OR-Tools, and SGE) compared to a basic Input-Output (IO) prompting approach for solving Job Scheduling Problems. The results are broken down by the number of jobs (n) and machines (m) used in the problem instances.

This table presents the performance improvement of the Self-Guiding Exploration (SGE) method compared to several baseline methods (Input-Output, Chain-of-Thought, Self-Refine, and Decomposition) across six different combinatorial problems (Assignment, Knapsack, Bin Packing, Traveling Salesman, Vehicle Routing, and Job Scheduling) using two different Large Language Models (LLMs), GPT-4 and Gemini-1.5. The improvement is measured as the percentage reduction in cost compared to the Input-Output baseline. Higher values indicate better performance.
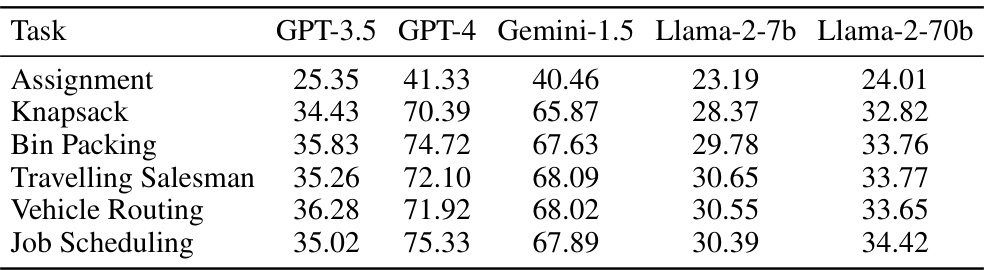
This table presents the performance improvement of the Self-Guiding Exploration (SGE) method compared to four baseline methods (Input-Output, Chain-of-Thought, Self-Refine, and Decomposition) across six combinatorial problems (Assignment, Knapsack, Bin Packing, Traveling Salesman, Vehicle Routing, and Job Scheduling) using GPT-4 and Gemini-1.5 language models. The improvement is measured as a percentage reduction in cost compared to the Input-Output baseline. The table also shows the results for the Chain-of-Thought (CoT) approach, using majority voting.

This table presents the performance improvement of the Self-Guiding Exploration (SGE) method compared to several baseline methods (IO, CoT, Refine, Decomp) for solving six combinatorial problems (Assignment, Knapsack, Bin Packing, TSP, VRP, Job Scheduling) using two different LLMs (GPT-4 and Gemini-1.5). The improvement is calculated as a percentage relative to the Input-Output (IO) baseline method and represents the percentage reduction in cost achieved by each method. Higher percentages indicate better performance.

This table presents the performance improvement of the Self-Guiding Exploration (SGE) method compared to several baseline methods (Input-Output, Chain-of-Thought, Self-Refine, and Decomposition) for six different combinatorial problems (Assignment, Knapsack, Bin Packing, Traveling Salesman, Vehicle Routing, and Job Scheduling) using two different large language models (GPT-4 and Gemini-1.5). The improvement is measured as the percentage reduction in cost compared to the Input-Output baseline. The table highlights SGE’s superior performance.

This table presents the percentage improvement in cost achieved by the Self-Guiding Exploration (SGE) method compared to four baseline methods (Input-Output, Chain-of-Thought, Self-Refine, and Decomposition) across six different combinatorial problems (Assignment, Knapsack, Bin Packing, Traveling Salesman, Vehicle Routing, and Job Scheduling) using two large language models (GPT-4 and Gemini-1.5). The improvement is calculated relative to the Input-Output baseline and is presented as a percentage. The table also shows results using a Chain-of-Thought baseline with the number of candidates equal to the number of thought trajectories generated by SGE.
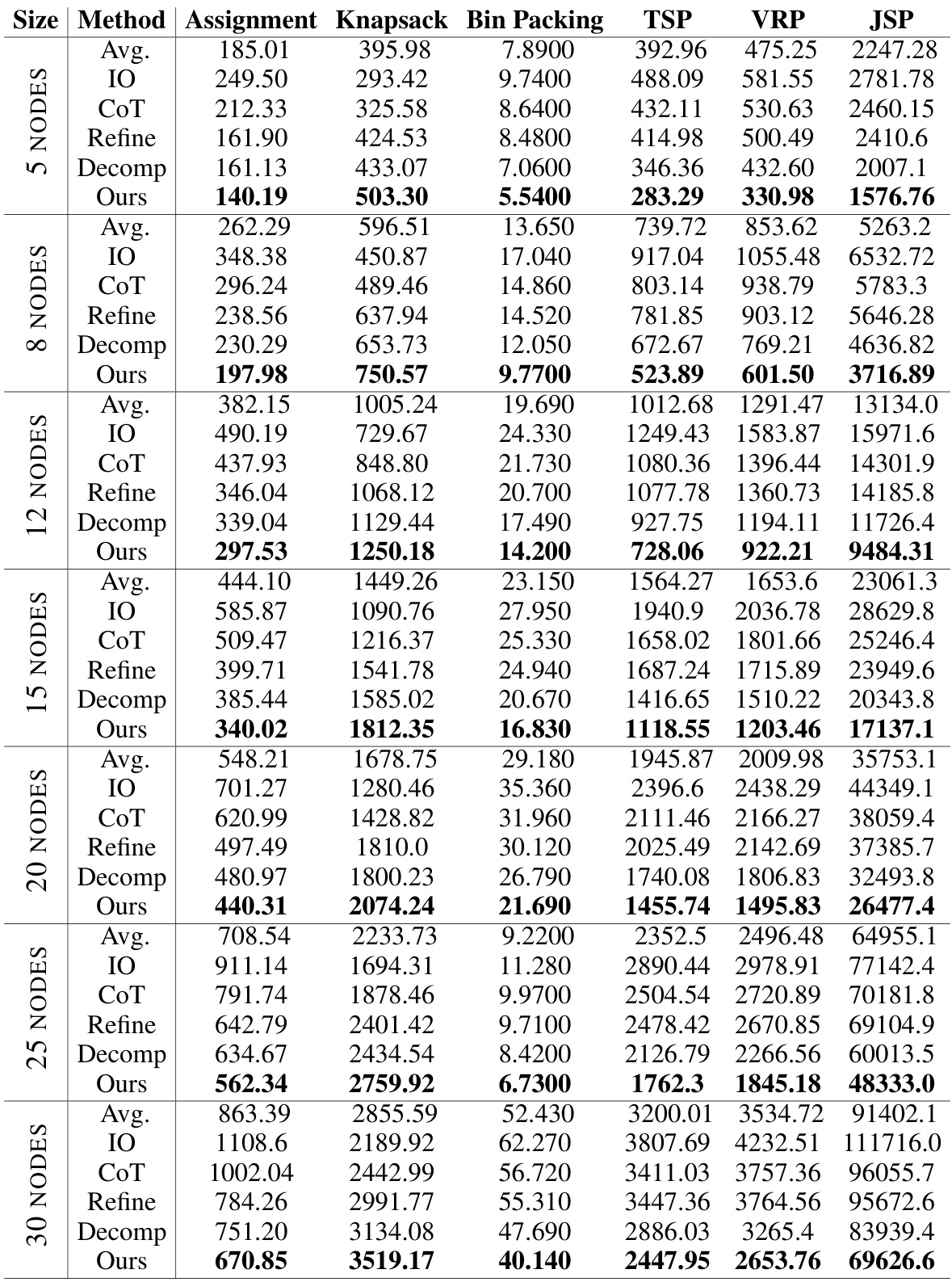
This table presents the performance improvement of the Self-Guiding Exploration (SGE) method compared to other baseline methods (Input-Output, Chain-of-Thought, Self-Refine, and Decomposition) for six different combinatorial problems (Assignment, Knapsack, Bin Packing, Traveling Salesman, Vehicle Routing, and Job Scheduling) using two different Large Language Models (LLMs), GPT-4 and Gemini-1.5. The improvement is measured as a percentage reduction in cost compared to the Input-Output baseline.
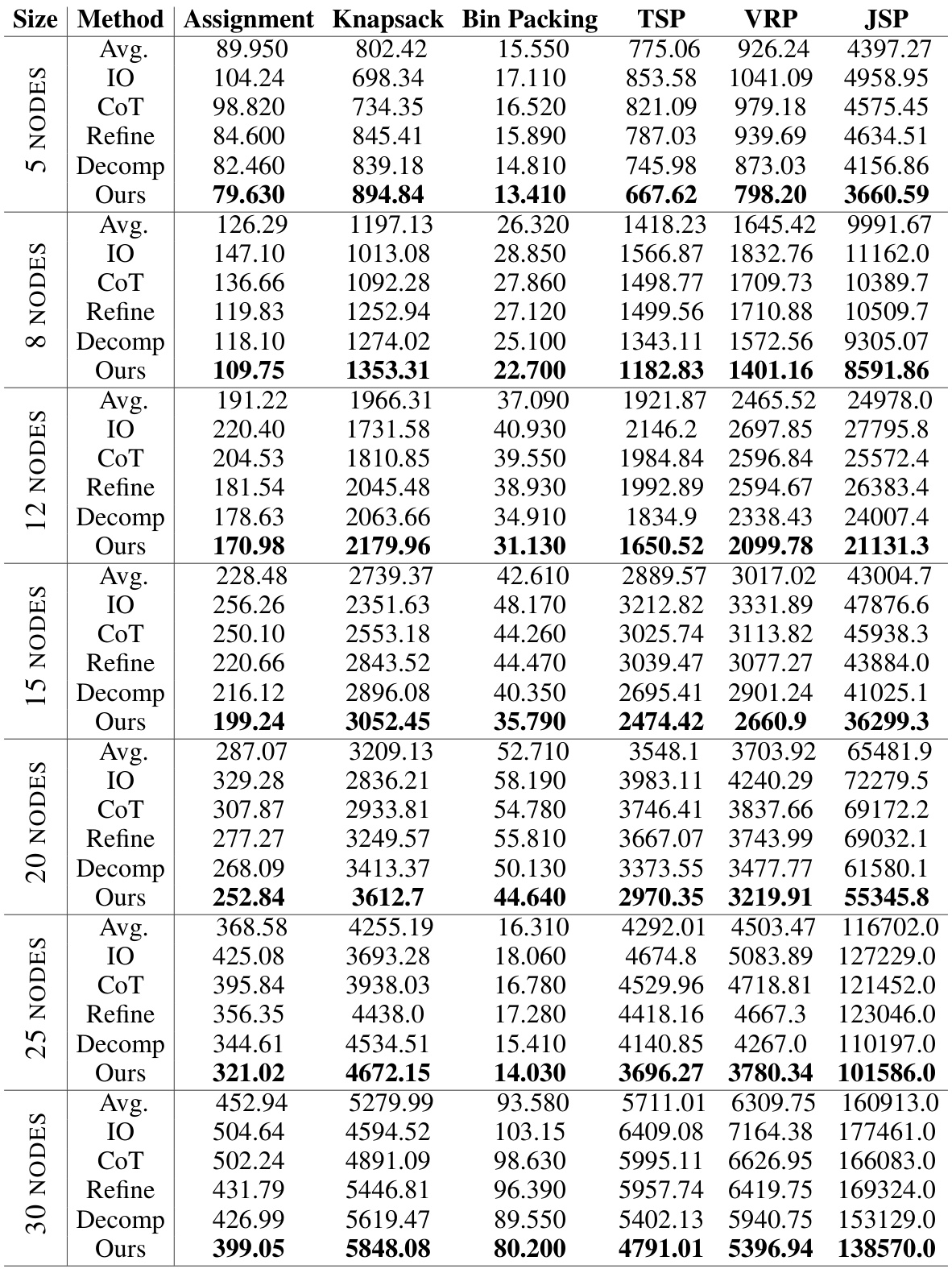
This table presents the performance improvement of the Self-Guiding Exploration (SGE) method compared to four baseline methods (Input-Output (IO) Direct Prompting, Chain-of-Thought Prompting, Self-Refine Prompting, and Decomposition Prompting) across six different combinatorial problems (Assignment, Knapsack, Bin Packing, Traveling Salesman, Vehicle Routing, and Job Scheduling). The improvements are calculated as a percentage relative to the IO baseline, showing how much better SGE performed in terms of cost optimization. The table also includes results using both GPT-4 and Gemini-1.5 language models.

This table presents the performance improvement of the Self-Guiding Exploration (SGE) method compared to several baselines (Input-Output, Chain-of-Thought, Self-Refine, and Decomposition) on six combinatorial problems (Assignment, Knapsack, Bin Packing, Traveling Salesman, Vehicle Routing, and Job Scheduling) using two different large language models (LLMs): GPT-4 and Gemini-1.5. The improvement is measured as the percentage reduction in cost compared to the Input-Output baseline. The table highlights the superior performance of SGE across all tasks and models.
Full paper#