↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Asynchronous Stochastic Gradient Descent (ASGD) is vital for training large-scale machine learning models. However, existing research provides limited insights into its generalization ability, often relying on stringent assumptions that don’t reflect real-world scenarios. This restricts practical applications and theoretical understanding. Prior work yields either vacuous or overly pessimistic results.
This paper tackles these issues by establishing sharper generalization bounds for ASGD under less restrictive assumptions. It employs the ‘on-average model stability’ concept and achieves non-vacuous bounds, even for non-smooth situations (using Hölder continuity). The study also examines excess generalization error to further refine the analysis. The authors validate their findings through extensive experiments on various machine learning tasks, providing concrete evidence of ASGD’s improved stability and reduced generalization error with appropriately increased delays.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses limitations in understanding the generalization performance of Asynchronous SGD (ASGD), a widely used algorithm in large-scale machine learning. By providing sharper generalization bounds under weaker assumptions and validating findings empirically, it improves our theoretical understanding and offers practical guidance for optimizing ASGD in various applications. This work opens avenues for further research into the stability and generalization of ASGD in non-smooth settings and non-convex problems, significantly impacting the field of distributed machine learning.
Visual Insights#

This figure shows the generalization error for three different machine learning tasks (convex optimization, computer vision, and natural language processing) as a function of the number of asynchronous training iterations. Different lines represent different average delays (τ). The results show a general trend of increasing generalization error with more iterations, but also demonstrate that increasing the average delay can mitigate this effect and improve generalization performance.

The table compares the assumptions and results of three different studies on the generalization of asynchronous SGD. It highlights the differences in the required assumptions (Lipschitz and smoothness) and the resulting generalization error bounds. This allows readers to quickly assess the relative strengths and weaknesses of each approach and the advancements made by the current work.
In-depth insights#
Async SGD Stability#
Analyzing asynchronous stochastic gradient descent (Async SGD) stability requires a nuanced understanding of the algorithm’s inherent challenges. The asynchronous nature introduces delays in gradient updates, which can lead to model inconsistency and affect convergence. Existing research often relies on strong assumptions like Lipschitz continuity and smoothness of loss functions to provide stability bounds. However, these assumptions are not always met in real-world applications. The paper addresses this gap by analyzing Async SGD’s stability under weaker assumptions, providing tighter bounds. This involves exploring different stability notions like uniform stability and on-average model stability to capture diverse aspects of the asynchronous behavior. Further investigation focuses on how factors like asynchronous delays, learning rates, model initialization, and the number of iterations influence the stability. The results highlight that appropriately increasing the asynchronous delay can actually improve stability, contrasting some conventional wisdom. Non-vacuous and practical bounds are presented, advancing our comprehension of Async SGD’s stability in diverse settings.
Generalization Bounds#
The study delves into generalization bounds, a critical aspect of machine learning, focusing on asynchronous stochastic gradient descent (ASGD). It aims to improve upon existing bounds, which are often pessimistic or based on overly restrictive assumptions like Lipschitz continuity and smoothness. The core contribution lies in establishing sharper bounds under weaker assumptions, relaxing the need for Lipschitz continuity and replacing smoothness with the more general Hölder continuity. This broadened applicability is significant, as many practical loss functions do not satisfy strict smoothness requirements. The analysis provides insights into how factors like asynchronous delays, model initialization, and the number of training samples and iterations impact generalization. The results demonstrate that appropriately increasing asynchronous delays can, counter-intuitively, improve generalization, a finding validated through extensive empirical testing. Overall, the work contributes to a more nuanced understanding of ASGD’s generalization behavior and offers valuable theoretical support for practical applications.
Non-smooth ASGD#
The exploration of “Non-smooth ASGD” in the research paper is a significant contribution, as it addresses a limitation of existing ASGD analysis which typically relies on smoothness assumptions. Relaxing the smoothness requirement to the weaker Hölder continuous assumption is crucial as it expands the applicability of the theoretical findings to a wider range of loss functions frequently encountered in machine learning, such as the hinge loss. The study’s investigation into the impact of asynchronous delays, model initialization, and the number of training samples on generalization error under this weaker condition is insightful. The results demonstrate that even without smoothness, ASGD maintains similar generalization properties, suggesting the robustness of the algorithm. This research is important because it moves beyond the restrictive assumptions of previous work and provides a more realistic and practically relevant analysis of ASGD’s generalization capabilities.
Empirical Validation#
The empirical validation section of a research paper is crucial for demonstrating the practical applicability and effectiveness of the proposed methods. A strong empirical validation should not only present results, but also provide a thorough methodology, justifying the experimental design and choices. Careful consideration should be given to datasets used, ensuring they are relevant and representative of real-world scenarios. The evaluation metrics selected should align directly with the paper’s claims, and sufficient details on the experimental setup should allow for reproducibility by other researchers. Robust statistical analysis, including error bars and appropriate significance tests, is necessary to support claims of improved performance. The inclusion of ablative studies and comparisons to existing methods further strengthens the validity of the results. Furthermore, a comprehensive discussion of the results is needed, interpreting them in light of the theoretical findings and highlighting limitations or unexpected behaviors. A thoughtful analysis should reveal valuable insights and potentially address open research questions, leading to broader implications for the field.
Future Directions#
The study’s significant contribution lies in establishing sharper generalization error bounds for asynchronous SGD under weaker assumptions. Future research could explore tighter high-probability bounds to reduce the learning rate’s dominance in generalization. Additionally, extending the analysis to non-convex scenarios presents a substantial challenge, requiring investigation into whether asynchronous updates remain approximately non-expansive in such settings. Moreover, empirical findings suggest asynchronous training can be beneficial even with delay-independent learning rates, warranting further theoretical exploration. Finally, investigating the impact of different learning rate strategies and their interaction with asynchronous delays on both stability and generalization would yield valuable insights. This detailed analysis will enhance understanding of asynchronous SGD’s theoretical properties and optimize its application in large-scale machine learning.
More visual insights#
More on figures
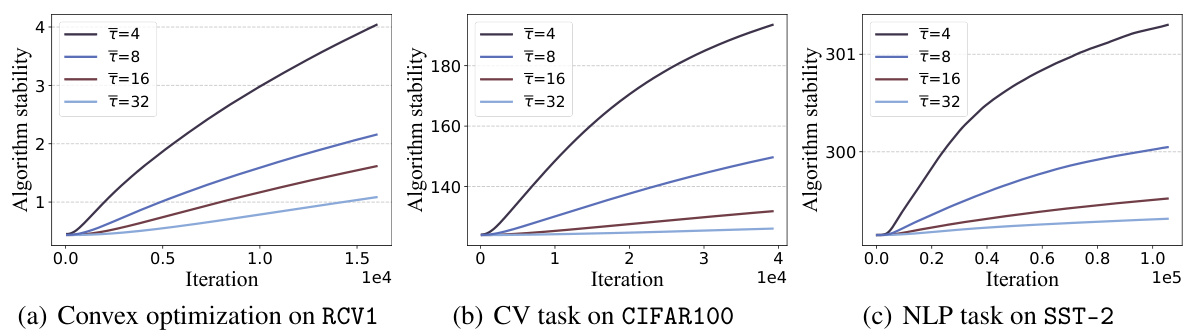
This figure shows how the on-average model stability changes with the number of training iterations and the average delay (τ) in three different machine learning tasks: convex optimization on RCV1, computer vision (CV) task on CIFAR100, and natural language processing (NLP) task on SST-2. As the number of iterations increases, the stability decreases for all delay values. The stability is better for larger delay values (τ).
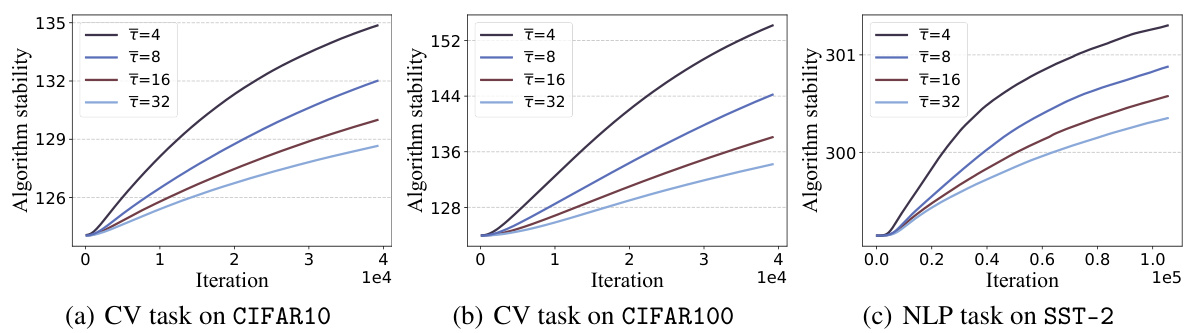
This figure shows how the on-average model stability changes with respect to the number of training iterations and the average asynchronous delay (τ). Across three different machine learning tasks (convex optimization, computer vision, and natural language processing), the stability generally decreases as the number of iterations increases. However, increasing the average delay tends to improve the stability, suggesting that a larger delay mitigates some negative effects of asynchronous updates.
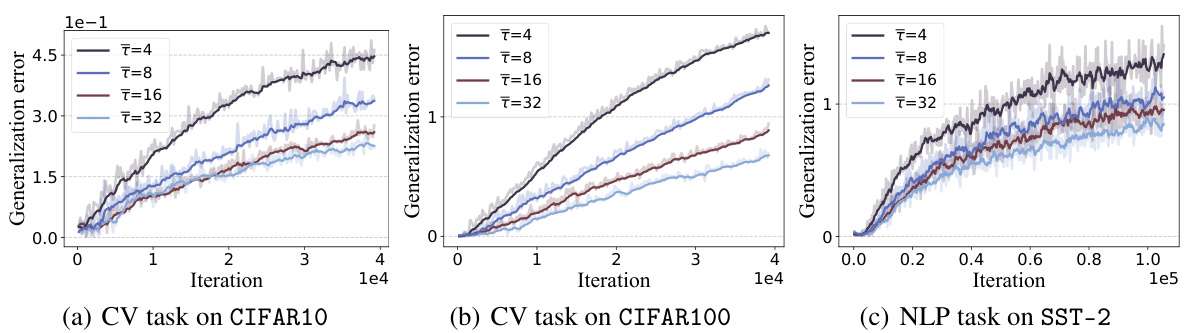
This figure shows the generalization error for three different machine learning tasks (convex optimization, computer vision, and natural language processing) when trained using the Asynchronous Stochastic Gradient Descent (ASGD) algorithm. The x-axis represents the number of iterations during training, and the different colored lines represent different average delays (τ). The figure demonstrates that increasing the average delay can mitigate the negative impact of asynchronous updates on generalization performance, especially as the number of training iterations increases.

This figure shows the generalization error curves for three different machine learning tasks (convex optimization, computer vision, and natural language processing) trained using the Asynchronous Stochastic Gradient Descent (ASGD) algorithm. The x-axis represents the number of training iterations, and different colored lines represent different average delays (τ) in the ASGD algorithm. The results demonstrate that increasing the asynchronous delay (τ) can improve generalization performance, especially in the later stages of training. However, as the training iterations increase, the generalization error tends to worsen, regardless of the delay.
Full paper#



















