TL;DR#
Reinforcement learning (RL) algorithms often struggle with non-stationary optimization landscapes due to continuously changing objectives, leading to instability and suboptimal performance. Existing methods, like target networks and clipped policy updates, attempt to mitigate this issue but lack theoretical grounding. Adam, a widely used optimizer, relies on a global timestep assumption that breaks down in non-stationary settings.
This paper introduces Adam-Rel, a modified Adam optimizer that uses a relative timestep within each epoch. This simple modification prevents large updates resulting from objective changes. Through rigorous experiments on Atari and Craftax, the authors demonstrate that Adam-Rel significantly outperforms standard Adam and other related methods. The study also offers a theoretical analysis explaining the benefits of the proposed method and showcases its effectiveness in handling various types of non-stationarity.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses a critical limitation in reinforcement learning (RL) optimization, improving the stability and performance of deep RL algorithms. Its findings are relevant to current research trends focusing on robust and efficient RL, and its proposed solution (Adam-Rel) is straightforward to implement and highly effective. This work opens up new avenues for research into improving optimizer design for non-stationary environments, and also provides insight into the interactions between gradient dynamics and the optimization process. This method is directly applicable to many existing deep RL algorithms.
Visual Insights#
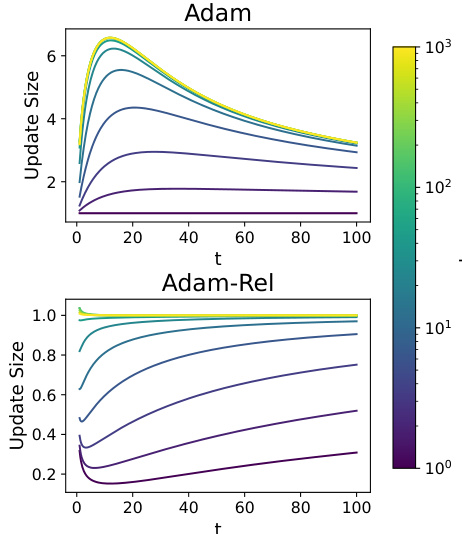
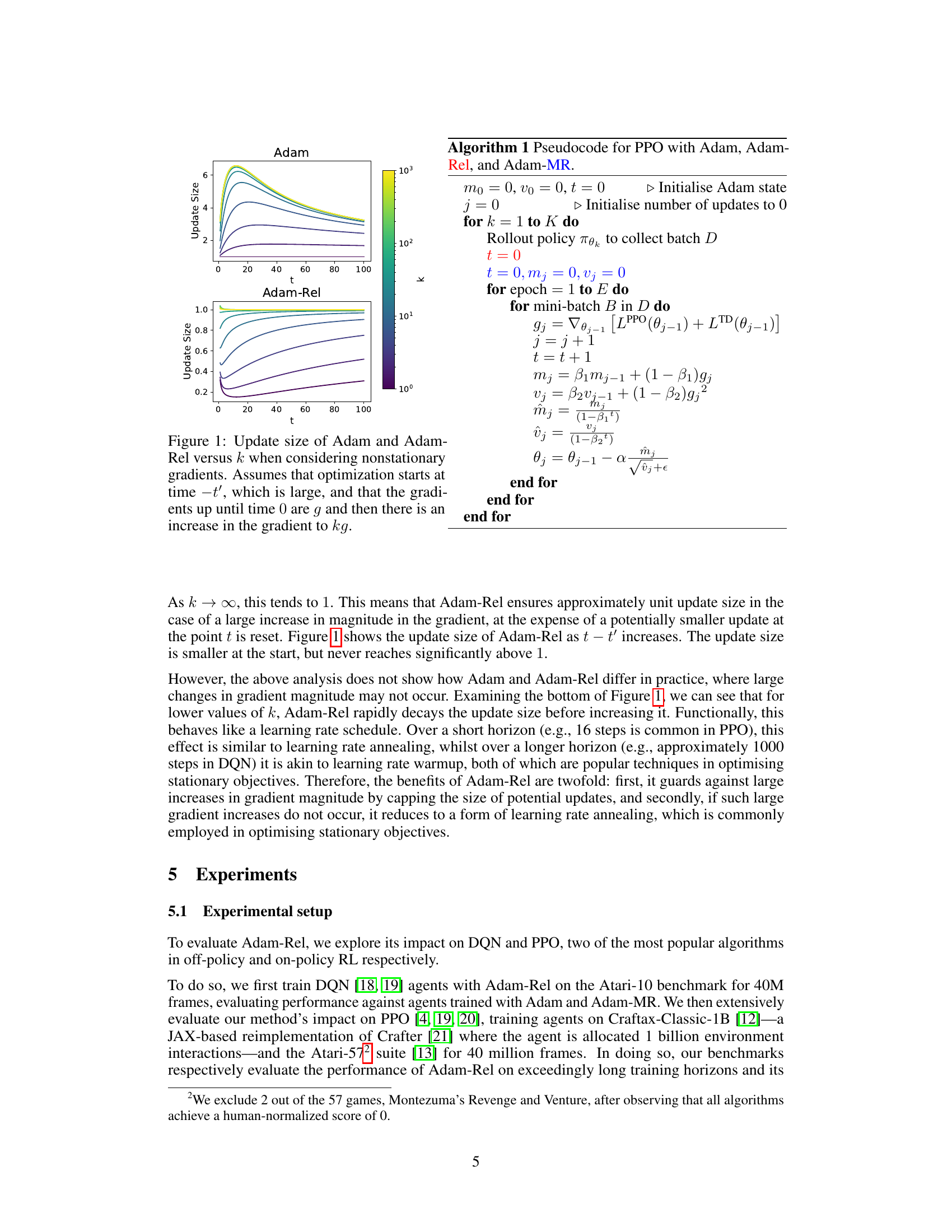
🔼 This figure compares the update size of Adam and Adam-Rel over time (t) for various scaling factors (k) applied to the gradient after a time step of 0. The top panel shows Adam’s behavior, illustrating that large updates occur after the gradient change, especially when the k value is large, demonstrating the effect of non-stationarity. The bottom panel shows Adam-Rel, highlighting that the update size remains bounded and converges to approximately 1, even with significant gradient changes.
read the caption
Figure 1: Update size of Adam and Adam-Rel versus k when considering nonstationary gradients. Assumes that optimization starts at time -t', which is large, and that the gradients up until time 0 are g and then there is an increase in the gradient to kg.
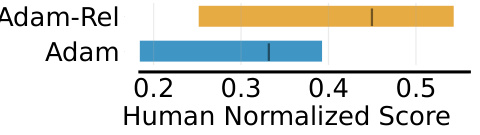
🔼 This figure compares the performance of Adam and Adam-Rel optimizers on the Atari-10 benchmark when using the Deep Q-Network (DQN) algorithm with Polyak averaging. Polyak averaging is a technique used to smooth the updates to the target network in DQN. The regressed median is used as a performance metric. The plot shows that Adam-Rel significantly outperforms Adam in this setting.
read the caption
Figure 7: Comparison of the regressed median on the Atari-10 benchmark of Adam and Adam-Rel for DQN with Polyak Averaging.
In-depth insights#
Adam’s Nonstationarity#
The concept of “Adam’s Nonstationarity” explores how the Adam optimizer, widely used in machine learning, behaves in the nonstationary environment typical of reinforcement learning (RL). Adam’s inherent reliance on past gradients assumes stationarity, meaning the data distribution remains consistent over time. However, in RL, the environment and the agent’s policy are constantly changing, leading to nonstationary gradients. This mismatch causes issues like large, unpredictable updates, hindering learning and potentially leading to instability. The paper likely investigates the theoretical analysis of Adam’s update rule under nonstationary conditions, revealing how past gradients can hinder adaptation in changing environments. It further proposes and evaluates modifications to the Adam algorithm, such as the introduction of a relative timestep or a reset mechanism, to improve performance in nonstationary settings. The analysis likely demonstrates that adapting Adam for RL requires modifications to better handle the dynamics of nonstationary data.
Adam-Rel: Epoch Reset#
The proposed Adam-Rel algorithm, featuring an epoch reset mechanism, offers a novel approach to mitigating the challenges of non-stationarity in reinforcement learning. By resetting Adam’s internal timestep at the beginning of each epoch, Adam-Rel prevents the accumulation of outdated momentum estimates that can hinder learning when the objective function changes due to policy updates or other factors. This approach effectively addresses gradient magnitude instability by avoiding excessively large updates in the presence of abrupt objective shifts. Unlike complete optimizer resets, Adam-Rel preserves valuable momentum information, leading to more efficient and stable learning. The epoch reset strategy elegantly transitions to learning rate annealing when gradient changes are gradual, further enhancing robustness and performance. Empirically, Adam-Rel demonstrates improvements in various RL benchmarks, showcasing its practical efficacy in addressing non-stationarity, a persistent issue in RL optimization. Its simple implementation and adaptability make it a promising solution for enhancing the reliability and efficiency of Adam in non-stationary reinforcement learning environments.
Atari & Craftax Tests#
The Atari and Craftax tests in the research paper served as crucial empirical evaluations to assess the performance of Adam-Rel, a novel optimizer designed to address nonstationarity in reinforcement learning. Atari, a benchmark known for its diverse and challenging games, provided a strong test of the algorithm’s robustness across multiple tasks with varying degrees of complexity and dynamics. Similarly, Craftax, with its procedural generation of environments, offered a unique assessment of the algorithm’s ability to adapt and optimize consistently even when facing significant environmental variability. The results from both benchmarks, demonstrating improved performance by Adam-Rel over standard Adam, confirmed the algorithm’s efficacy and emphasized its significant contribution to addressing the challenges presented by nonstationarity in RL.** The detailed analysis across these two very different testing environments provides compelling evidence supporting the claims made in the paper. The selection of both on-policy and off-policy settings further strengthened the validity and generalizability of the findings.
Gradient Norm Analysis#
A Gradient Norm Analysis section would delve into the magnitude of gradients during training, exploring how these magnitudes change over time and in response to various factors. Nonstationarity in reinforcement learning (RL) would be a key focus, investigating how shifts in the objective function (e.g., due to target network updates) impact gradient norms. The analysis might involve comparing gradient norms across different algorithms (e.g., Adam vs. Adam-Rel) or different phases of training (e.g., early vs. late stages). Visualizations, such as plots of gradient norms over time, would be crucial for illustrating the observed patterns and relationships. Furthermore, the analysis could compare empirical findings with theoretical predictions of gradient behavior under nonstationary conditions. This comparison would help assess the accuracy and limitations of theoretical models and potentially guide the development of more robust optimization techniques for RL. An important aspect would be to examine the relationship between gradient norms and algorithm performance, such as return or success rates. Finally, the analysis should also discuss the implications of gradient norm behavior for algorithm stability and design choices. In short, Gradient Norm Analysis is critical for understanding RL optimization and improving its efficacy.
Future Work: RL Scope#
Future research directions in reinforcement learning (RL) could explore several promising avenues. Extending Adam-Rel to continuous non-stationary settings is crucial, as many RL algorithms face this challenge. Investigating the interplay between Adam-Rel and other RL techniques, such as different learning rate schedules or exploration strategies, would offer valuable insights. Analyzing the impact of Adam-Rel on more diverse RL tasks and environments, beyond the Atari and Craftax benchmarks, is important for assessing its generalizability. Furthermore, a deeper theoretical understanding of the interaction between non-stationarity and optimization algorithms, particularly Adam’s update rule, could lead to the development of more robust and efficient methods. Finally, directly addressing the plasticity loss problem—the inability of models to adapt to changing objectives—using this approach warrants future investigation.
More visual insights#
More on figures

🔼 This figure shows how the update size of the Adam and Adam-Rel optimizers change over time when there is a sudden increase in the gradient magnitude. The x-axis represents the timestep, and the y-axis represents the update size. The figure shows that Adam produces much larger updates after the gradient increase than Adam-Rel, which maintains a relatively stable update size. This demonstrates how Adam-Rel handles non-stationarity better than Adam.
read the caption
Figure 1: Update size of Adam and Adam-Rel versus k when considering nonstationary gradients. Assumes that optimization starts at time -t', which is large, and that the gradients up until time 0 are g and then there is an increase in the gradient to kg.
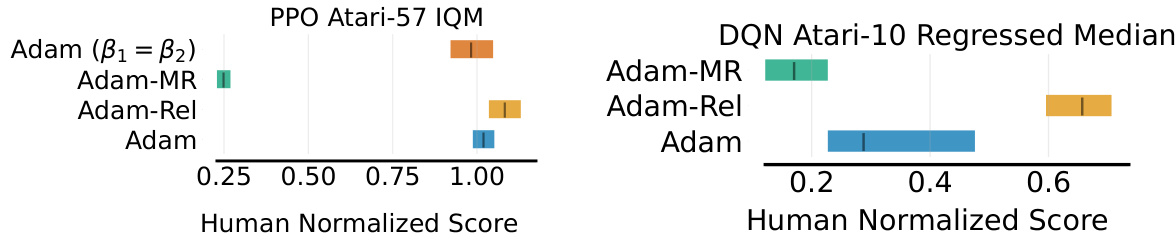
🔼 This figure compares the performance of four different Adam-based optimization methods (Adam, Adam-Rel, Adam-MR, and Adam with β₁=β2) on two reinforcement learning tasks: Atari-57 (using Proximal Policy Optimization or PPO) and Atari-10 (using Deep Q-Network or DQN). The Atari-10 results show the median performance across a subset of the Atari games. The chart displays the human-normalized scores for each method, with error bars indicating the 95% confidence intervals. The results show the relative effectiveness of each Adam variant in improving performance compared to standard Adam, highlighting the improvement offered by Adam-Rel.
read the caption
Figure 2: Performance of Adam-Rel, Adam, Adam-MR, and Adam (β₁ = β2) for PPO and Adam, Adam-MR and Adam-Rel for DQN on Atari-57 and Atari-10 respectively. Atari-10 uses a subset of Atari tasks to estimate median performance across the whole suite. Details can be found in [14]. Error bars are 95% stratified bootstrapped confidence intervals. Results are across 10 seeds except for Adam (β₁ = β2), which is 3 seeds.

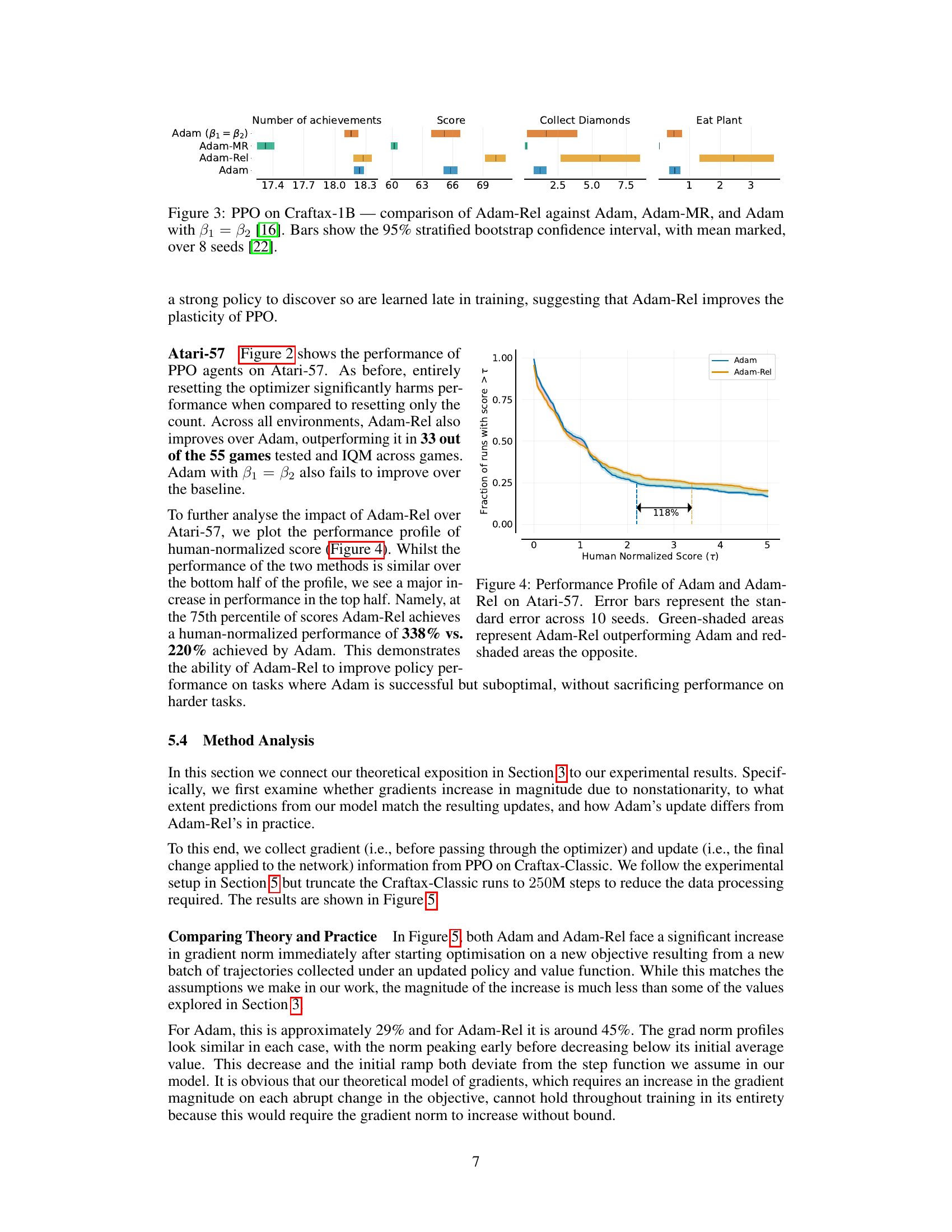
🔼 This figure compares the performance of four different optimization algorithms (Adam, Adam-Rel, Adam-MR, and Adam with β₁ = β2) used in the Proximal Policy Optimization (PPO) algorithm on the Craftax-1B environment. The performance metrics shown are the number of achievements, score (geometric mean of success rates for achievements), success rate of collecting diamonds, and success rate of eating plants. Adam-Rel demonstrates consistent improvement over the other methods.
read the caption
Figure 3: PPO on Craftax-1B comparison of Adam-Rel against Adam, Adam-MR, and Adam with β₁ = β2 [16]. Bars show the 95% stratified bootstrap confidence interval, with mean marked, over 8 seeds [22].
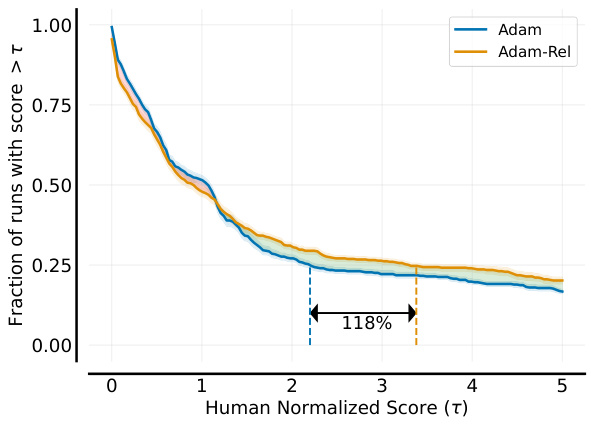
🔼 This figure shows the performance profile of Adam and Adam-Rel on Atari-57, comparing the fraction of runs achieving a score greater than a certain human-normalized score (τ). The shaded areas highlight where one method surpasses the other. The key takeaway is Adam-Rel’s significant performance improvement over Adam, especially in the higher-performing percentile, indicating its ability to enhance performance in challenging tasks without compromising performance on simpler tasks.
read the caption
Figure 4: Performance Profile of Adam and Adam-Rel on Atari-57. Error bars represent the standard error across 10 seeds. Green-shaded areas represent Adam-Rel outperforming Adam and red-shaded areas the opposite.
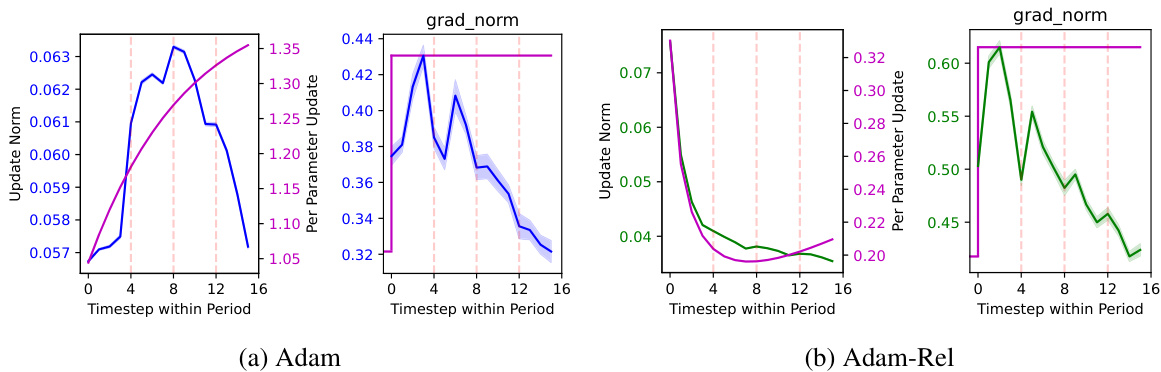
🔼 This figure shows the update size of both Adam and Adam-Rel plotted against time (t) for different values of k. The parameter k represents a sudden increase in the gradient magnitude at time t=0. The top plot shows the update size for Adam, demonstrating a large peak exceeding 1 before converging back to 1. The bottom plot shows Adam-Rel’s update size which stays bounded close to 1, highlighting the advantage of using relative timesteps in handling non-stationary gradients.
read the caption
Figure 1: Update size of Adam and Adam-Rel versus k when considering nonstationary gradients. Assumes that optimization starts at time -t', which is large, and that the gradients up until time 0 are g and then there is an increase in the gradient to kg.
🔼 This figure shows the update size of the Adam and Adam-Rel optimizers plotted against time (t) for different values of k, which represents the factor by which the gradient increases at time t=0. The top plot shows that when using Adam, a sudden increase in the gradient (large k) leads to an overshoot in the update size before slowly converging back to 1. The bottom plot shows that Adam-Rel avoids this overshoot, maintaining an update size near 1 even for large k. This demonstrates Adam-Rel’s ability to handle non-stationary gradients.
read the caption
Figure 1: Update size of Adam and Adam-Rel versus k when considering nonstationary gradients. Assumes that optimization starts at time -t', which is large, and that the gradients up until time 0 are g and then there is an increase in the gradient to kg.
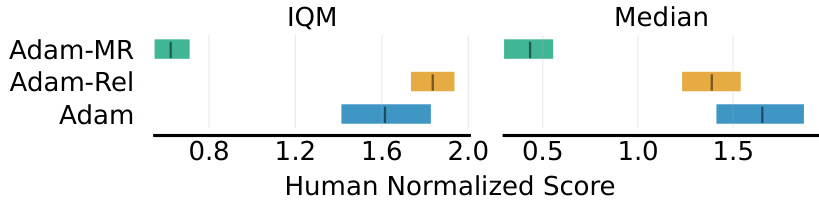
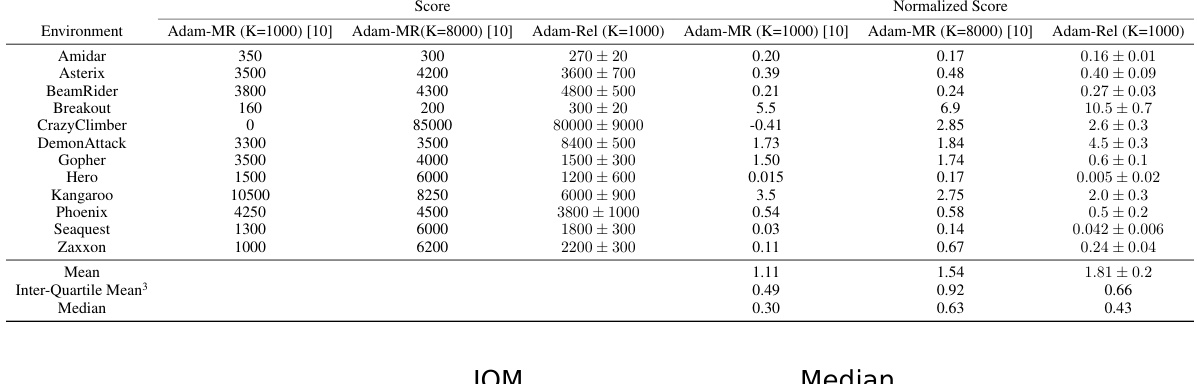
🔼 This figure compares the performance of three Adam variants (Adam-MR, Adam-Rel, and Adam) on the Atari games used in the Asadi et al. [10] study. The performance is measured using two metrics: the interquartile mean (IQM) and the median. The IQM represents the average performance excluding extreme outliers, while the median provides a robust central tendency measure. The results show that Adam-Rel generally outperforms the baselines.
read the caption
Figure 6: Comparison of the inter-quartile mean and median of Adam-MR, Adam-Rel and Adam on the Atari games evaluated on in Asadi et al. [10].
More on tables
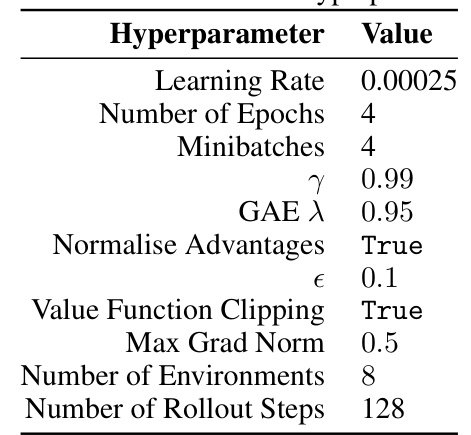
🔼 This table shows the hyperparameters used for the Proximal Policy Optimization (PPO) algorithm with the Adam optimizer on the Atari benchmark. It lists the learning rate, number of epochs, minibatch size, discount factor (γ), generalized advantage estimation (GAE) λ parameter, whether advantages were normalized, the value function clipping parameter (ε), whether value function clipping was used, max gradient norm, number of environments, and the number of rollout steps. These settings were used in the experiments evaluating the Adam-Rel algorithm’s performance.
read the caption
Table 2: Atari Adam PPO hyperparameters
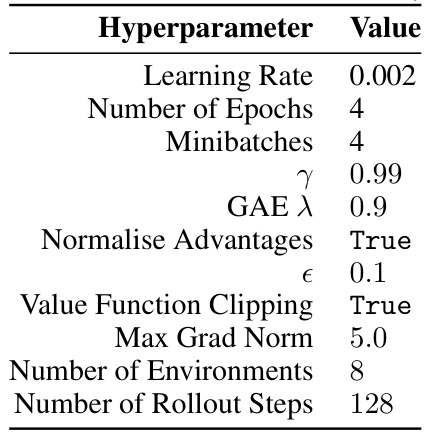
🔼 This table lists the hyperparameters used for both Adam-Rel and Adam-MR in the Proximal Policy Optimization (PPO) algorithm on the Atari benchmark. It specifies values for learning rate, number of epochs, minibatches, gamma (γ), Generalized Advantage Estimation (GAE) lambda (λ), whether advantages are normalized, epsilon (ϵ), whether value function clipping is used, the maximum gradient norm, the number of environments used for training, and the number of rollout steps.
read the caption
Table 3: Atari Adam-Rel and Adam-MR PPO hyperparameters
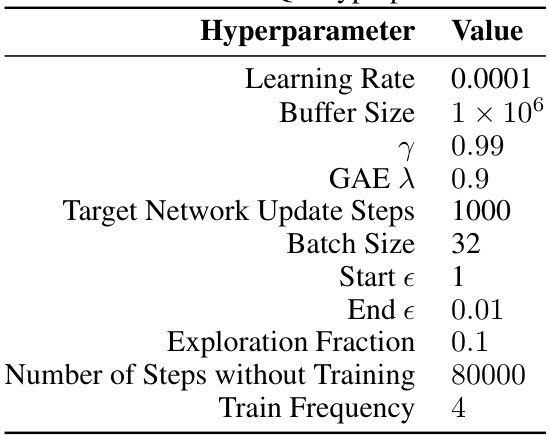
🔼 This table lists the hyperparameters used for the Deep Q-Network (DQN) algorithm in the Atari-10 experiments. It includes the learning rate, replay buffer size, discount factor (γ), generalized advantage estimation (GAE) λ parameter, target network update frequency, batch size, exploration rate (start and end epsilon), exploration fraction, number of steps without training, and train frequency.
read the caption
Table 4: Atari-10 DQN hyperparameters
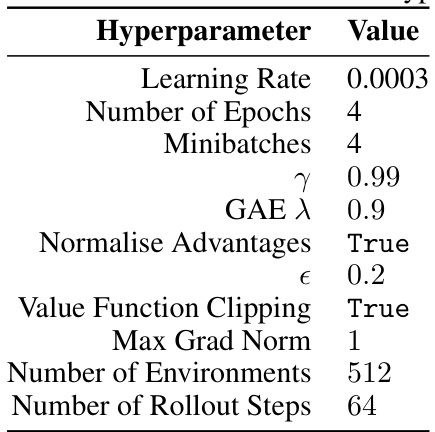
🔼 This table lists the hyperparameters used for the Proximal Policy Optimization (PPO) algorithm with Adam and Adam-MR optimizers on the Craftax environment. The hyperparameters include the learning rate, number of epochs, minibatches, gamma (γ), Generalized Advantage Estimation lambda (GAE λ), whether advantages were normalized, value function clipping epsilon (ϵ), maximum gradient norm, number of environments, and number of rollout steps. Note that the hyperparameters were tuned separately for Adam and Adam-MR.
read the caption
Table 5: Craftax Adam and Adam-MR PPO hyperparameters
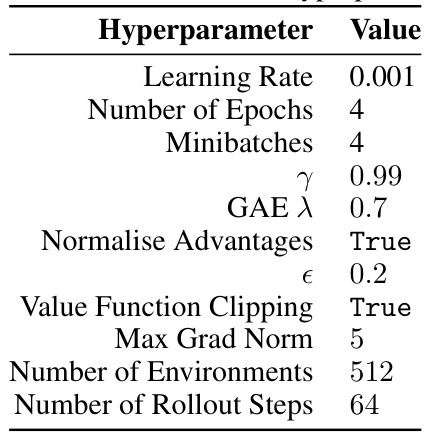
🔼 This table presents the hyperparameters used for the Adam-Rel algorithm during the Craftax experiments. It includes the learning rate, the number of epochs and minibatches used in training, the discount factor (γ), the generalized advantage estimation lambda (GAE λ), whether advantages were normalized, the value function clipping parameter (ε), whether value function clipping was used, the maximum gradient norm, the number of environments used for training, and the number of rollout steps.
read the caption
Table 6: Craftax Adam-Rel hyperparameters
Full paper#