↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Large language models and AI image generators are increasingly trained on AI-generated data. This practice can lead to a phenomenon called “model collapse,” where the model’s performance drastically degrades, resulting in nonsensical outputs. This paper investigates model collapse in high-dimensional regression using Gaussian data. The researchers found that training a model on data from multiple generations of AI-generated data causes the model’s performance to worsen linearly with the number of iterations.
The researchers use a linear regression setting with Gaussian data to study model collapse. They derive analytical formulas that quantify how the test error increases with iterations of AI-generated data, considering various factors like covariance spectrum, regularization, noise level, and dataset size. They find that even with no noise, catastrophic model collapse can occur. They propose a simple regularization strategy to lessen the effects of model collapse. Their theoretical findings are validated with experiments, showing the impact of retraining on model performance and offering practical solutions for mitigating model collapse.
Key Takeaways#
Why does it matter?#
This paper is crucial because it provides a theoretical framework to understand and quantify model collapse, a significant issue in the field of large language models and AI-generated data. The findings offer practical guidance on mitigating model collapse by adjusting regularization parameters, directly impacting the development and reliability of future AI systems. The detailed analysis opens avenues for further research on more complex architectures and datasets.
Visual Insights#

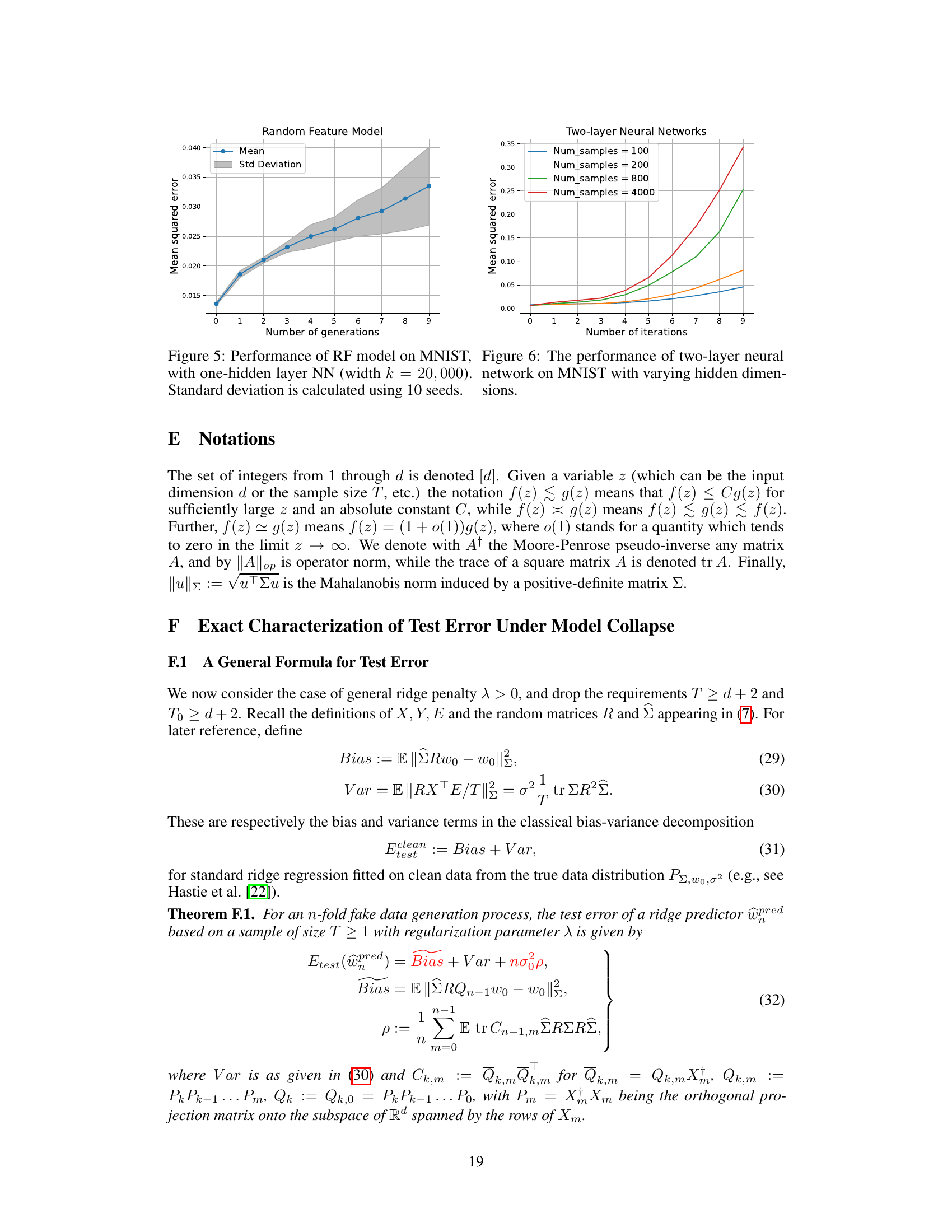
This figure displays two plots illustrating model collapse in high-dimensional regression with Gaussian data. Plot (a) shows test error evolution for different sample sizes (T), ridge regularization parameters (λ), and training data generations (n) using an isotropic covariance spectrum (Σ = Id). The U-shaped curves highlight an optimal regularization parameter. Plot (b) uses a power-law covariance spectrum, showing test error for adaptive regularization (λ = T−lcrit) and varying sample sizes. The broken lines represent the theoretical results from Theorem 4.1 and Theorem 5.1. Both plots showcase how test error increases linearly with the number of model iterations (n), as predicted by the theory.
In-depth insights#
Model Collapse#
The phenomenon of model collapse, where the performance of AI models degrades upon retraining with AI-generated data, is a significant concern. This paper offers valuable insights into this issue, particularly focusing on the impact of iterative retraining on synthesized data in high-dimensional regression. The core finding is that model collapse is not merely a consequence of noise but is intrinsically tied to the data generation process itself. Even without label noise, catastrophic collapse can occur in over-parameterized models due to a bias introduced by the iterative process. The paper’s rigorous analysis uses random matrix theory, effectively demonstrating how the bias increases with each generation. This leads to a change in the scaling laws of test error, highlighting the importance of adapting regularization techniques to effectively counter the negative effects of model collapse. The study provides crucial theoretical insights, offering a pathway to building more robust AI systems that are less susceptible to this critical failure mode. The analysis shows the effects on bias and variance separately, demonstrating that the issue isn’t merely one of increased variance but is primarily about increasing bias that becomes catastrophic in overparameterized settings. The results strongly suggest the need for careful consideration and design of training regimes to mitigate the risks associated with model collapse.
Bias-Variance#
The bias-variance tradeoff is a central concept in machine learning, representing the balance between a model’s ability to fit the training data (low bias) and its ability to generalize to unseen data (low variance). High bias indicates the model is too simplistic, failing to capture the underlying patterns in the data, leading to underfitting. High variance, conversely, suggests an overly complex model that’s highly sensitive to noise and fluctuations in the training data, resulting in overfitting. The optimal model minimizes both bias and variance, achieving a balance between these two opposing forces. The paper likely explores how the iterative retraining on synthetic data influences this tradeoff. Specifically, it investigates whether the process amplifies bias, variance, or both. It may demonstrate how the increase in bias, a consequence of training on inaccurate synthesized data, becomes increasingly prominent as the model iterates, while the variance component, related to model complexity and noise, exhibits a different behavior across various data regimes (under vs. over-parameterized) and covariance structures. Understanding these dynamics helps to refine model design and training strategies to avoid detrimental model collapse, thereby improving the overall generalization performance.
Scaling Laws#
Scaling laws in machine learning aim to characterize the relationship between model performance and various resource factors, like dataset size, model parameters, and computational power. Empirical scaling laws reveal power-law relationships, suggesting that improvements in these resources lead to predictable gains in performance. However, the presence of synthetic data generated by prior models significantly alters these relationships. The paper investigates how model collapse, caused by iterative retraining on synthetic data, impacts established scaling laws. It finds that synthetic data leads to modified scaling laws, where the rate of performance improvement slows down or even plateaus, demonstrating the significant negative effect of training exclusively on AI-generated data. This highlights a crucial limitation of relying on solely synthetic data for model training and emphasizes the need for careful consideration of the underlying data distribution when extrapolating scaling laws to new settings. The simple strategy based on adaptive regularization to mitigate model collapse is proposed.
Regularization#
Regularization is crucial in mitigating model collapse, a phenomenon where AI models trained on their own generated data exhibit performance degradation. The paper investigates this using high-dimensional regression, demonstrating that adaptive regularization, adjusting the regularization strength based on the amount of training data, is particularly effective in preventing catastrophic model failure. The authors derive analytical formulas showing how test error increases with the number of model iterations, highlighting the importance of controlling this increase through regularization. In the over-parametrized regime, where the number of model parameters exceeds the number of data points, even noise-free data can lead to exponentially fast model collapse, again emphasizing the vital role of regularization. Their findings suggest that optimal regularization strategies for clean data need significant adjustment when dealing with synthetic data, which underscores the complexity of training models in the current age of readily available synthetic data generation.
High-D Regimes#
The section on “High-D Regimes” in this research paper delves into the complexities of high-dimensional settings, where both the number of data points and the dimensionality of the feature space grow substantially. The authors acknowledge that analyzing the test error in these regimes demands advanced mathematical tools from Random Matrix Theory (RMT). RMT is crucial for handling the asymptotic behavior of large random matrices, which accurately reflect the high-dimensional nature of the data in such cases. The core idea is to use RMT to obtain analytic formulae for test error. These formulae explicitly capture the interplay between various hyperparameters such as the covariance structure of the data, the regularization strength, the level of label noise, and the amount of data available. By leveraging the power of RMT, the authors manage to derive new scaling laws that show how test error evolves in high-dimensional settings. These scaling laws offer a significant advance in understanding model collapse, especially in the context of training models iteratively on AI-generated data. The results are particularly important because they highlight the limitations of previously established regularization strategies in the presence of synthetic data. Specifically, the authors show how optimal regularization schemes need to be adapted in high-dimensional regimes where the data has been recursively synthesized.
More visual insights#
More on figures
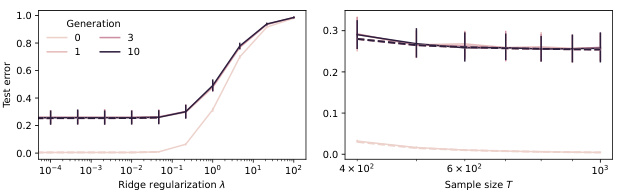
This figure shows the evolution of test error for different sample sizes (T), different levels of ridge-regularization (λ), and training data from different generations (n) of fake data for both isotropic and power-law covariance spectrums. The plots demonstrate the impact of model collapse and show the existence of an optimal regularization parameter (sweet spot) for large values of n. The broken lines in the plots correspond to the theoretical results from Theorem 4.1 and Theorem 5.1. Appendix D provides additional experimental details.
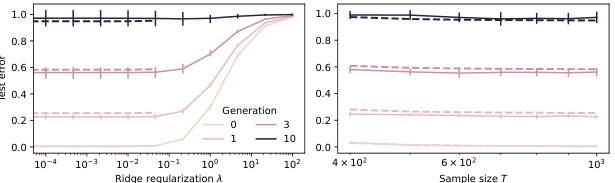
This figure shows the impact of model collapse on test error in two different settings. (a) Isotropic covariance spectrum shows how test error evolves with different ridge regularization parameters and sample sizes, illustrating the existence of an optimal regularization parameter. (b) Power-law covariance spectrum demonstrates test error changes with adaptive regularization. The figures reveal how test error changes with different generations of synthetic data and highlights the effects of model collapse.

This figure illustrates the theoretical framework of the paper. It shows how the model is trained iteratively on synthetic data generated from previous generations, which introduces noise at each step. The process starts with original model parameters ŵo and original data (X0, Y0). Subsequent models (ŵ1 to ŵn) are trained on data synthesized using the previous generation’s model with added noise (σ0). Finally, a downstream model (wpred) is trained on the nth generation of synthetic data (Xn, Yn) with added noise (σ) and a regularization parameter (λ). The test error of the downstream model (wpred) is then evaluated against the ground truth labels (from ŵo).
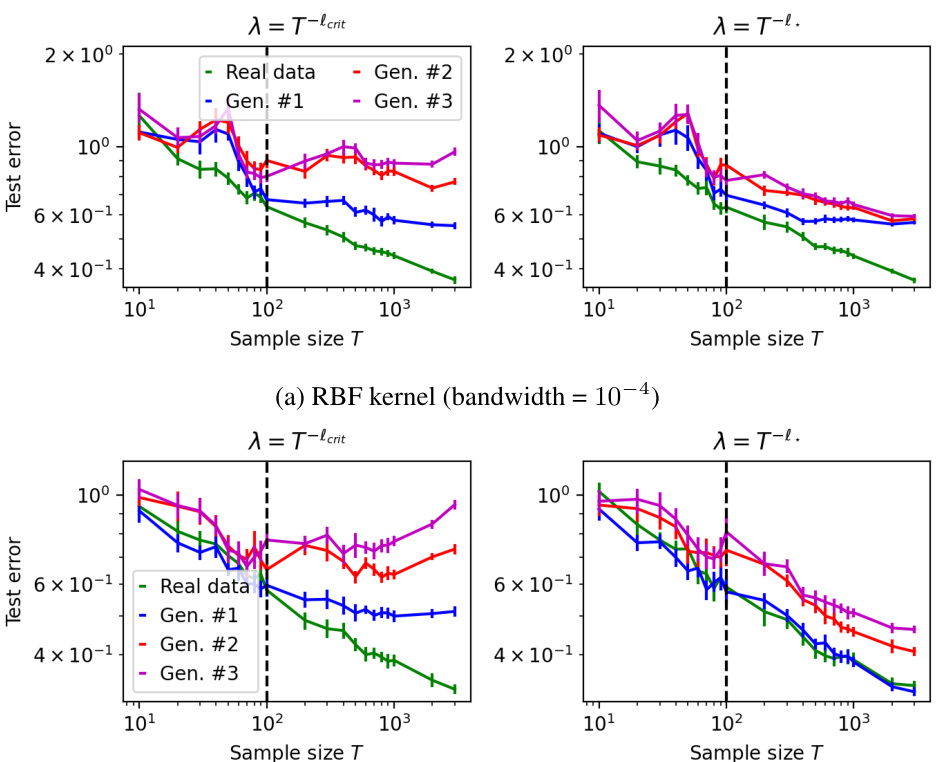
This figure shows the impact of training on synthetic data generated iteratively from previous generations. It compares the test error of kernel ridge regression models trained on real MNIST data versus those trained on synthetic data generated by iteratively retraining a model on its own outputs. The plots illustrate the ‘model collapse’ phenomenon, where the test error increases (and does not decrease) as the number of synthetic data generations increases.
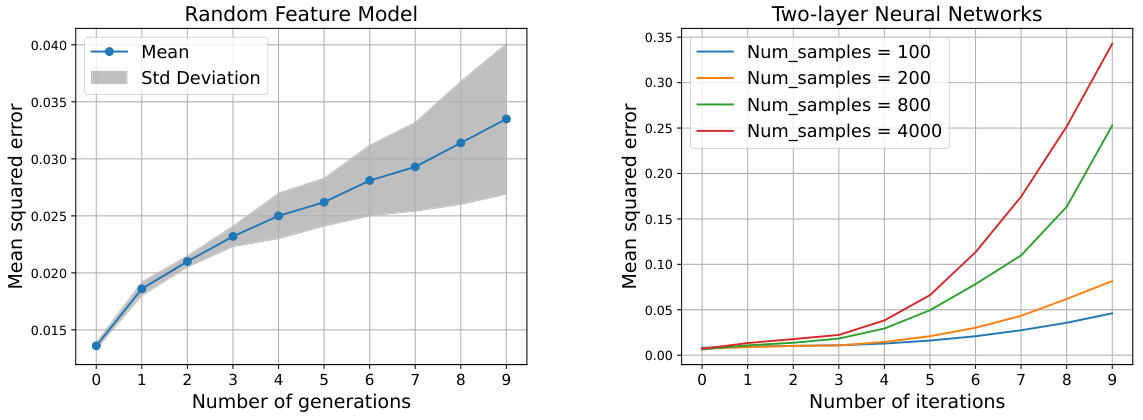
This figure demonstrates the evolution of test error as a function of different hyperparameters such as ridge regularization, sample size, and the number of generations of synthetic data. The plots show the test error for isotropic and power-law covariance spectrum scenarios, highlighting the effects of model collapse.
Full paper#