↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Federated learning (FL) faces challenges with clients having varying computational resources, hindering participation and impacting model training. Existing static and dynamic submodel extraction approaches have limitations: static methods are inflexible and fail to account for model evolution, while dynamic methods may compromise individual submodel performance. These limitations impact both the training speed and overall accuracy.
FIARSE addresses these issues through an importance-aware submodel extraction technique. It dynamically adjusts submodels based on parameter importance, enhancing model efficiency without requiring additional information beyond model parameters. FIARSE outperforms existing static and dynamic methods across various datasets and model sizes, demonstrating its ability to optimize both local submodel accuracy and global model convergence. Its theoretical analysis confirms a convergence rate comparable to state-of-the-art FL algorithms, solidifying its efficiency and effectiveness.
Key Takeaways#
Why does it matter?#
This paper is important because it tackles the crucial problem of model heterogeneity in federated learning, offering a novel solution that enhances efficiency and scalability in resource-constrained environments. The theoretical analysis and empirical results demonstrate its significant advantages over existing methods, opening up new avenues for research and development in heterogeneous federated learning.
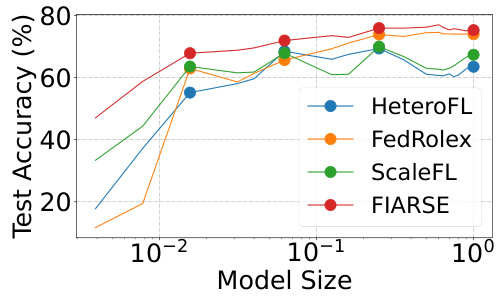
Visual Insights#

This figure shows the distribution of test accuracy achieved by different clients using four different submodel sizes (1/64, 1/16, 1/4, 1) for four different model-heterogeneous federated learning methods (HeteroFL, FedRolex, ScaleFL, and FIARSE). The x-axis represents the test accuracy, and the y-axis represents the number of clients achieving that level of accuracy. It provides a visual comparison of the performance of each method in terms of the distribution of client accuracy.

This table presents the test accuracy results of four different model sizes (1/64, 1/16, 1/4, 1.0) on CIFAR-10, CIFAR-100, and AGNEWS datasets. For each dataset and model size, it shows the average test accuracy across multiple clients (‘Local’) as well as the global model accuracy (‘Global’). The ‘Local’ accuracy reflects the performance of the submodel trained on each client’s local dataset, while the ‘Global’ accuracy reflects the performance of the aggregated global model.
In-depth insights#
FIARSE Algorithm#
The FIARSE algorithm innovatively addresses model heterogeneity in federated learning (FL) by dynamically constructing submodels tailored to individual clients’ computational constraints. Central to FIARSE is its importance-aware submodel extraction, which leverages the magnitude of model parameters as a proxy for their importance. This eliminates the need for additional overhead associated with calculating or storing separate importance scores. Instead, the algorithm iteratively incorporates parameters in descending order of magnitude, building each client’s submodel until the client’s capacity is reached. This dynamic approach contrasts with static methods, which extract submodels once and can’t adapt to parameter shifts during training, and improves upon dynamic techniques like FedRolex, which lack an explicit importance measure, potentially sacrificing submodel performance. The algorithm’s theoretical convergence analysis demonstrates a rate consistent with other state-of-the-art FL methods, showing that its adaptive submodel construction doesn’t hinder convergence. Empirical results on various datasets further solidify FIARSE’s superior performance, particularly for resource-constrained clients.
Importance Metrics#
In evaluating model parameters’ importance, several strategies exist, each with strengths and limitations. Magnitude-based metrics, such as the absolute value or L1 norm, offer simplicity and computational efficiency, but might overlook parameters crucial despite small magnitudes. Gradient-based approaches use gradients to quantify the impact of a parameter’s change on model output. While more sensitive than magnitude-based methods, they demand additional computation and are sensitive to hyperparameter tuning. Hessian-based methods, involving the second derivative, offer higher-order insights but suffer from immense computational cost, often limiting their use to smaller models. Information-theoretic metrics, like mutual information, assess a parameter’s impact on the overall model uncertainty and capture non-linear relationships; however, they are computationally challenging. Shapley values provide a fair attribution by evaluating the marginal contribution of each parameter, but their calculation becomes increasingly expensive with larger models. The choice of importance metric hinges on the trade-off between accuracy, computational cost, and interpretability, making it a crucial aspect of model optimization and interpretation.
Convergence Analysis#
The Convergence Analysis section of a research paper is crucial for establishing the reliability and effectiveness of the proposed algorithms. A rigorous convergence analysis provides a theoretical guarantee of the algorithm’s ability to reach a solution, often specifying the rate of convergence. This analysis usually involves making assumptions about the problem structure (e.g., convexity, smoothness, boundedness of gradients) and the algorithm’s parameters (e.g., step sizes, regularization). Key aspects to look for include the types of assumptions made and their justification, the proof techniques employed (e.g., Lyapunov functions, contraction mappings), and the resulting convergence rates. A strong convergence analysis will not only prove convergence but also provide insights into factors influencing the convergence speed, such as problem parameters or algorithm hyperparameters. Limitations and potential improvements regarding the convergence analysis should also be discussed. For instance, the analysis might only hold under specific assumptions which may not always hold in practice. Analyzing the impact of relaxing these assumptions or proposing methods to address the limitations enhances the paper’s value.
Experimental Results#
The Experimental Results section of a research paper is crucial for validating the claims and hypotheses presented. A strong results section will include clear visualizations (graphs, tables) that are easy to interpret and directly support the paper’s conclusions. Statistical significance, including error bars and p-values, should be meticulously reported to demonstrate the reliability of findings. The section needs to clearly define metrics used for evaluation and justify the chosen ones. Comparison with baselines or previous works is essential to demonstrate the novelty and improvement of the proposed approach. The discussion should be comprehensive and insightful, analyzing not only the successes, but also limitations and potential biases of the results and acknowledging any unexpected outcomes or areas for future work. A well-written Experimental Results section significantly enhances the impact and credibility of a research paper by providing convincing evidence of its contributions.
Future Works#
The “Future Works” section of a research paper on FIARSE, a novel federated learning approach, could explore several promising avenues. Extending FIARSE to handle more complex model architectures beyond ResNet and RoBERTa is crucial, evaluating its performance on diverse, large-scale datasets. A thorough investigation into different threshold selection strategies beyond the proposed TopK method is necessary to optimize submodel construction, potentially using adaptive or dynamic techniques based on real-time feedback. Theoretical analysis could be deepened, proving tighter convergence bounds or exploring scenarios with non-convex objectives and heterogeneous client participation more rigorously. Furthermore, exploring neuron-wise importance as opposed to parameter-wise importance, and investigating hardware-aware optimization techniques to minimize computational overhead, especially for resource-constrained edge devices, are worthwhile directions. Finally, examining the impact of varying communication round frequencies and different client sampling strategies on the overall performance of FIARSE would offer valuable insights. These are but a few of the numerous opportunities for advancing the field of model-heterogeneous federated learning.
More visual insights#
More on figures

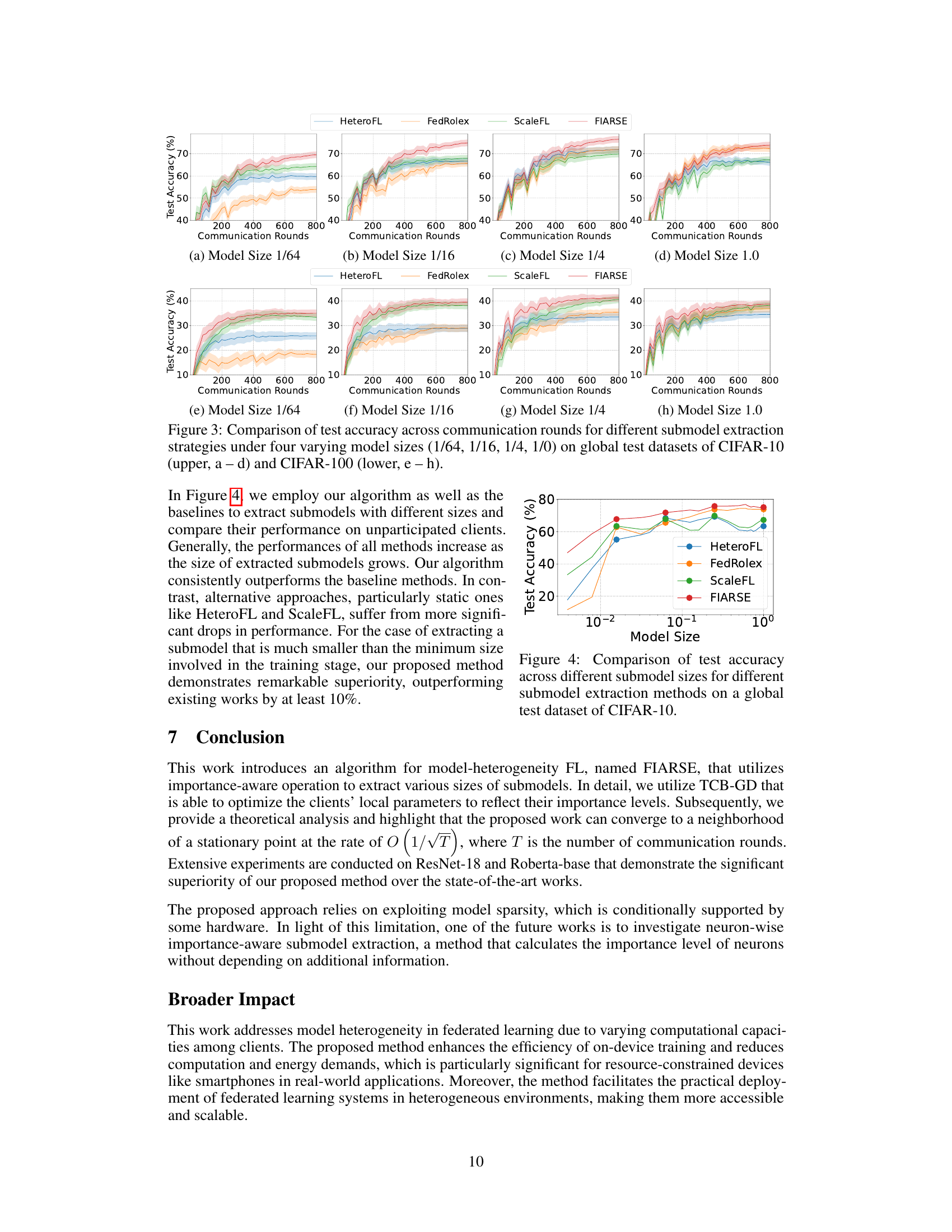
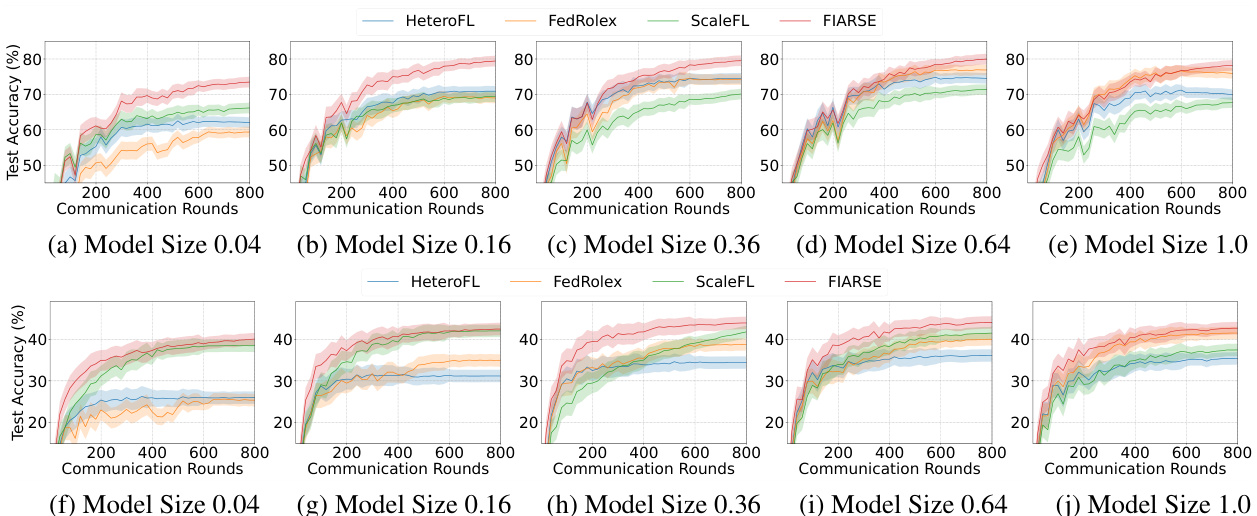
This figure compares the performance of four different submodel extraction methods (HeteroFL, FedRolex, ScaleFL, and FIARSE) on CIFAR-10 and CIFAR-100 datasets across four different model sizes (1/64, 1/16, 1/4, and 1.0). The x-axis represents the communication rounds, and the y-axis represents the test accuracy. The plots show the test accuracy trend over communication rounds for each method and model size. The shaded areas around the lines likely represent confidence intervals or standard deviations indicating variability in the results across different runs. The results suggest how different methods affect the model training over time, highlighting FIARSE’s superior and faster convergence in achieving higher test accuracy.
This figure compares the performance of four different submodel extraction methods (HeteroFL, FedRolex, ScaleFL, and FIARSE) on CIFAR-10 and CIFAR-100 datasets. The test accuracy is plotted against the number of communication rounds for four different model sizes (1/64, 1/16, 1/4, and 1.0). The plots show how the test accuracy evolves over the communication rounds and how the performance varies across different model sizes for each method. The upper panel shows the results for CIFAR-10, while the lower panel shows the results for CIFAR-100.
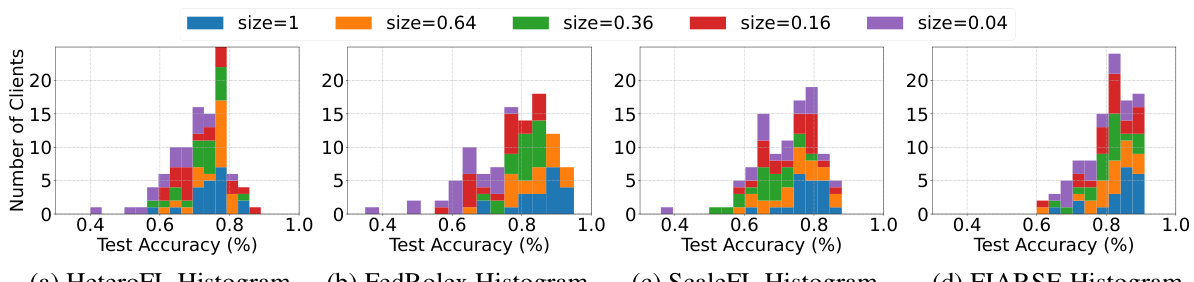
The figure displays histograms showing the distribution of test accuracy achieved by different clients using four different model sizes (1/64, 1/16, 1/4, 1.0) for four different submodel extraction methods (HeteroFL, FedRolex, ScaleFL, and FIARSE). Each bar in the histogram represents a range of test accuracy, and the height of the bar indicates the number of clients that achieved test accuracy within that range. This visualization helps to compare the performance of the different methods in terms of how well they adapt to clients with different computational capabilities, represented by the varying model sizes. It shows the distribution of successful clients which provides insights into the effectiveness of each submodel extraction method.
This figure compares three different submodel extraction methods in federated learning: static, dynamic, and importance-aware (the proposed FIARSE method). It visually illustrates how a global model is partitioned into submodels for different clients across two consecutive training rounds (t and t+1). Solid lines represent parameters included in the client’s submodel, while dashed lines show excluded parameters. The thickness of the lines in the importance-aware approach indicates the relative importance of the parameters.

The figure shows the test accuracy of different submodel extraction methods (HeteroFL, FedRolex, ScaleFL, and FIARSE) across communication rounds for four different model sizes (1/64, 1/16, 1/4, 1.0) on CIFAR-10 and CIFAR-100 datasets. The upper part shows results for CIFAR-10 and the lower part for CIFAR-100. Each sub-figure shows the accuracy trend for a specific model size.
More on tables

This table presents the test accuracy results for four different submodel sizes (1/64, 1/16, 1/4, 1.0) across three datasets (CIFAR-10, CIFAR-100, and AGNews). The ‘Local’ columns show the average test accuracy achieved by the submodels on each client’s local dataset, illustrating the performance of locally customized models. The ‘Global’ column indicates the test accuracy achieved by the global model (aggregated from the submodels) on a global test dataset. This comparison helps to evaluate both the effectiveness of the submodels in adapting to local data and their generalization capability to unseen data.
This table lists the hyperparameters used in the experiments for CIFAR-10, CIFAR-100, and AGNews datasets. It specifies the number of local epochs, batch size, communication rounds, optimizer used (SGD or AdamW), learning rate range (log10 scale), and momentum values.

This table presents the test accuracy results under four different submodel sizes (1/64, 1/16, 1/4, 1.0) for three datasets: CIFAR-10, CIFAR-100, and AGNews. For each dataset and submodel size, it shows the test accuracy on local datasets (‘Local’), representing the average accuracy across clients’ individual local test sets, and the global test accuracy (‘Global’), which indicates the accuracy of the aggregated global model tested on a common global test set. The results highlight the performance of different model sizes for different model heterogeneity scenarios.

This table presents the test accuracy results achieved by FIARSE and other baseline methods under five different submodel sizes (0.04, 0.16, 0.36, 0.64, 1.0) across three datasets: CIFAR-10, CIFAR-100, and AGNews. For each dataset and model size, it shows both the local accuracy (average accuracy across all clients’ local test sets) and the global accuracy (accuracy of the globally aggregated model on a global test set). This allows for a comparison of how well each method generalizes and how well it performs on resource-constrained devices (smaller submodels).

This table presents the results of an ablation study on CIFAR-100 dataset to demonstrate the effectiveness of the proposed FIARSE. It compares the performance of FIARSE against a pruning-greedy baseline and a layer-wise FIARSE variant across four different submodel sizes (1/64, 1/16, 1/4, 1.0). The ‘Local’ columns show the average test accuracy across all clients, while the ‘Global’ columns show the test accuracy of the globally aggregated model. The average accuracy across all model sizes is also provided for both local and global evaluations. This allows for a comparison of the proposed method’s performance against simpler baselines with different submodel extraction strategies.

This table presents the test accuracy results obtained using five different submodel sizes (0.04, 0.16, 0.36, 0.64, 1.0) on the CIFAR-10, CIFAR-100, and AGNews datasets. The results are categorized into ‘Local’ accuracy (evaluated on the local test datasets of each client) and ‘Global’ accuracy (evaluated using the global test dataset). This comparison helps assess the performance of the model at both the individual client level and the overall global level.
Full paper#