On the Complexity of Identification in Linear Structural Causal Models

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in causal inference and related fields because it significantly advances the understanding of the computational complexity of causal identification, a long-standing challenge. The new polynomial-space algorithm for generic identification and the hardness results for numerical identification provide valuable theoretical insights and pave the way for more efficient and robust causal discovery methods. This impacts research on algorithm design, model selection, and real-world applications.

Visual Insights

#

This figure shows a comparison of different methods for generic identification in linear structural causal models (SCMs). The methods are represented as nodes, and arrows indicate that one method subsumes (includes all the identifiable instances of) another. Green boxes signify methods with known polynomial-time algorithms, red boxes denote methods without such algorithms or proven to be NP-hard, and a blue box highlights the complete methods. The figure visually represents the relationships and completeness of various approaches to identifying causal parameters in linear SCMs.

In-depth insights

#

PSPACE ID Algo

#

A PSPACE ID algorithm for causal inference in linear structural causal models (SCM) would represent a significant advancement. Current methods often rely on Gröbner basis computations, leading to doubly exponential time complexity. A PSPACE algorithm would guarantee a solution within polynomial space, improving efficiency dramatically for larger models, although the time complexity may still be exponential. The development of such an algorithm would likely involve innovative techniques for solving polynomial systems, possibly leveraging results from computational algebraic geometry or symbolic computation. The algorithm’s practicality would depend heavily on the size of the polynomial systems generated from the SCM. A key challenge lies in managing the complexity of these systems, potentially through clever variable substitutions or approximations. While a PSPACE solution wouldn’t guarantee a fast algorithm in practice, it significantly alters the theoretical landscape, implying that the identification problem is not as computationally intractable as initially believed. Understanding this theoretical improvement opens new avenues for exploration in causal discovery, focusing on refinements for speed or specific model structures. Future research could explore methods to improve its runtime performance in practice, potentially through heuristics or tailored methods for particular types of SCMs.

Numerical ID Hardness

#

The section on ‘Numerical ID Hardness’ likely investigates the computational complexity of identifying causal parameters in linear structural causal models (SCMs) given a covariance matrix. The authors probably demonstrate that determining the uniqueness of a parameter set explaining the observed data is a computationally hard problem. This hardness result is significant because it implies that finding the true causal parameters from observational data alone is likely intractable for large or complex systems. The core argument likely relies on a reduction from a known hard problem, such as the existential theory of the reals (ETR) or a variant thereof. This reduction would involve constructing an SCM instance whose identifiability is equivalent to the solution of the hard problem. By showing this equivalence, the authors provide evidence that numerical identifiability is computationally hard, indicating that even with sufficient data, the task of identifying the causal parameters uniquely might be computationally infeasible.

Generic ID in PSPACE

#

The heading ‘Generic ID in PSPACE’ suggests a significant finding in the computational complexity of generic identifiability within a specific causal model. PSPACE (Polynomial Space) signifies a class of computational problems solvable using an amount of memory polynomial to the input size, contrasting with potentially harder classes like EXP (Exponential time). The term ‘Generic ID’ likely refers to determining the model parameters under the assumption of generic identifiability, meaning the parameters are uniquely determined almost everywhere in the parameter space, except for a lower-dimensional set of measure zero. This result implies a polynomial space algorithm exists to solve for these parameters, a considerable improvement upon previous algorithms which often had double-exponential complexity. This constitutes a major advance in the efficiency of causal inference, shifting the theoretical understanding of the problem’s computational difficulty and paving the way for potentially more efficient practical algorithms. The algorithm’s design would be interesting, as it likely leverages the properties of polynomial space computations for effectively managing the search space or constructing a solution. The exact nature of the causal model itself (linear, non-linear etc.) would also strongly influence the practicality and implications of this result.

Beyond Linearity

#

A research section titled ‘Beyond Linearity’ in a causal inference paper would likely explore the limitations of linear structural causal models (SCMs) and discuss extensions to handle nonlinear relationships. Nonlinearity is prevalent in real-world phenomena, and linear SCMs, while mathematically tractable, often fail to capture the complexity of these systems. The section would probably delve into methods for identifying and estimating causal effects in the presence of nonlinearity, potentially including techniques like nonparametric methods, generalized additive models, or neural networks. A key challenge is the increased computational cost and the potential for identifiability issues in nonlinear settings. The discussion might also encompass model diagnostics and sensitivity analysis to evaluate the robustness of inferences to deviations from linearity. Finally, the section might compare and contrast the performance of nonlinear methods against linear approaches, highlighting the trade-offs between accuracy and interpretability.

Cyclic SCMs

#

In the realm of causal inference, cyclic Structural Causal Models (SCMs) present a significant challenge compared to their acyclic counterparts. Cycles introduce the possibility of feedback loops, where a variable’s effect influences its own cause, creating intricate dependencies not found in acyclic systems. This complexity significantly impacts identifiability—the ability to uniquely determine causal parameters from observational data. Standard identification methods often fail in cyclic SCMs, requiring novel approaches. Researchers are actively exploring techniques like those employing differential equations or advanced algebraic methods to address the challenges posed by feedback loops and the resulting non-linear relationships. Understanding and modeling cyclic SCMs is crucial for accurately representing real-world systems that frequently exhibit feedback mechanisms, improving our ability to draw reliable causal inferences. The computational complexity of identifying causal parameters also increases dramatically in the presence of cycles, demanding further research into efficient algorithms. A deeper understanding of cyclic SCMs is essential for progress in fields like biology, economics, and social sciences where feedback loops are pervasive.

More visual insights

#

More on figures

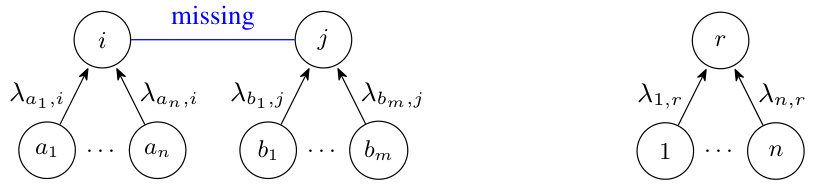
The figure shows two diagrams. The left diagram illustrates a bipartite graph with a missing edge between nodes in the top layer. The right diagram depicts a gadget used to store the value of each variable within a larger model; each variable xᵢ is represented by the edge Aᵢ,ᵣ. This gadget is a crucial component in a reduction proof used in the paper to establish the computational complexity of a problem.

This figure illustrates two key components within a larger graph structure used in a proof. The left panel displays a simplified view, showing a single ‘missing’ edge connecting nodes ‘r’ and ‘i’ and the directed edges from nodes ‘1…n’ into ‘r’. The right panel presents a more elaborate ‘gadget’ that represents a variable. This gadget involves adding multiple nodes (‘i’ and ‘j’ in the top layer and their corresponding nodes ‘i and ‘j in the bottom layer) and their interconnections, reflecting a specific type of mathematical constraint. The ‘missing’ edges represent equations that need to be satisfied and the purpose of the gadget is to encode the value of the variable ‘x into the structure of the graph.

Full paper

#