Provably Faster Algorithms for Bilevel Optimization via Without-Replacement Sampling

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it presents novel algorithms for bilevel optimization that are provably faster than existing methods. This is significant because bilevel optimization is crucial in many machine learning applications, including hyperparameter optimization and meta-learning. The proposed algorithms offer significant computational advantages, especially for large-scale problems, and the theoretical analysis provides strong guarantees on their performance. The work also opens new avenues for research into example-selection strategies and their impact on the efficiency of bilevel optimization algorithms.

Visual Insights

#

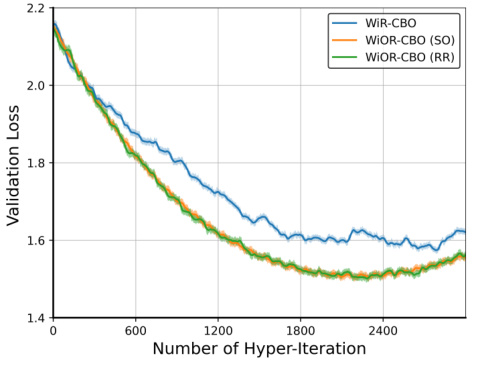
This figure compares three different sampling strategies used in the Invariant Risk Minimization task: independent sampling (WiR-CBO), shuffle-once (WiOR-CBO (SO)), and random-reshuffling (WiOR-CBO (RR)). The x-axis represents the number of hyper-iterations, and the y-axis represents the validation loss. The results show that the without-replacement sampling methods (shuffle-once and random-reshuffling) outperform the independent sampling method, converging to a lower validation loss.

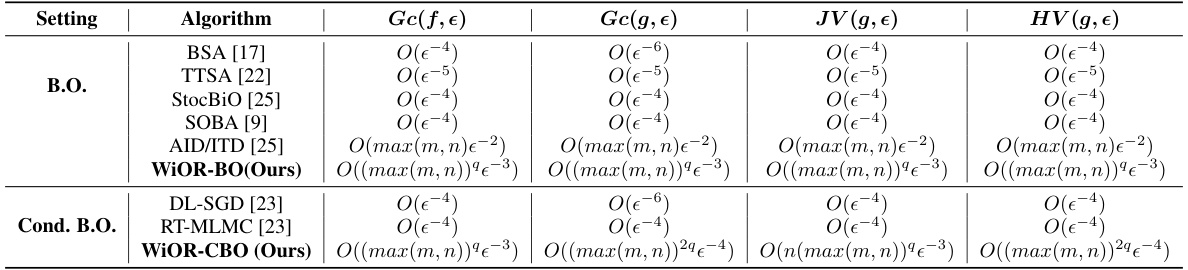
This table compares the computational complexity of various bilevel optimization algorithms in terms of gradient evaluations, Jacobian-vector products, and Hessian-vector products needed to find an e-stationary point. It shows the complexity for both standard and conditional bilevel optimization problems, highlighting the impact of different sampling strategies (independent vs. without-replacement). The table includes existing algorithms and the authors’ proposed methods (WiOR-BO and WiOR-CBO), demonstrating the improved convergence rate of the new algorithms.

In-depth insights

#

Bilevel Optimization

#

Bilevel optimization presents a significant challenge in optimization, involving the nested optimization of two problems. The inner problem is dependent on the solution of the outer problem, creating complex interdependencies. Recent advancements leverage stochastic gradient-based methods, mirroring successes in single-level optimization. However, a major hurdle is the increased computational cost from the inherent assumption of independent sampling. This paper tackles this by proposing without-replacement sampling strategies, demonstrating improved convergence rates compared to traditional methods relying on independent sampling. This approach is extended to encompass conditional bilevel optimization, showcasing broader applicability. The study also covers important special cases like minimax and compositional optimization. Numerical results on synthetic and real-world applications confirm the superiority of the proposed algorithms, highlighting the efficiency gains obtained through the novel example-selection methods. The theoretical analysis provides convergence guarantees and rate analyses. The research offers a compelling advancement in bilevel optimization techniques through careful consideration of sample efficiency.

Sampling Methods

#

The effectiveness of bilevel optimization algorithms hinges significantly on the employed sampling strategies. Traditional approaches often rely on independent sampling, where examples for estimating gradients are selected randomly with replacement at each iteration. This method, while straightforward, can be computationally expensive due to the nested nature of bilevel problems and the complexity of hypergradient calculations. The paper explores without-replacement sampling, a more efficient alternative. By sampling without replacement, the algorithm leverages information from previously sampled examples, improving the accuracy of gradient estimation and reducing overall computational cost. This is particularly advantageous in large-scale settings. Two prominent without-replacement strategies, random reshuffling and shuffle-once, are investigated, showcasing their ability to accelerate convergence compared to independent sampling. The paper rigorously analyzes the convergence rate of algorithms using both independent and without-replacement methods, highlighting the superior theoretical performance of the latter under certain conditions. The empirical validation further demonstrates the practical benefits of the proposed without-replacement sampling techniques, indicating significant speed improvements in the context of several real-world applications.

Algorithm Analysis

#

The algorithm analysis section of a research paper is crucial for establishing the validity and efficiency of the proposed methods. A strong analysis should begin by clearly stating the assumptions made about the problem setting (e.g., convexity, smoothness, data distribution). These assumptions are critical because they directly influence the theoretical guarantees that can be derived. The core of the analysis typically involves deriving bounds on the convergence rate, showing how quickly the algorithm approaches a solution as a function of key parameters (e.g., number of iterations, sample size, step size). Tight bounds are highly desirable, providing strong evidence of efficiency. Furthermore, the analysis might involve comparing the algorithm’s performance to existing methods under similar assumptions. This comparative analysis helps position the proposed work within the broader literature and highlight any improvements or unique contributions. Finally, proofs or detailed proof sketches are essential to support any theoretical claims made. The level of rigor should match the overall ambition of the paper. While asymptotic results are often valuable, it is sometimes beneficial to explore the performance of the algorithms in the finite-sample regime to provide a more realistic picture of the algorithm’s practical behavior. In many cases, numerical experiments that validate the theoretical findings are also expected.

Experimental Results

#

The effectiveness of the proposed algorithms is rigorously evaluated in the ‘Experimental Results’ section through a series of experiments. The experiments encompass both synthetic and real-world datasets, allowing for a comprehensive assessment of the methods’ performance in diverse settings. Quantitative metrics, such as convergence rates and validation performance, are meticulously presented, and the results convincingly demonstrate the superiority of the proposed approaches over existing state-of-the-art methods. The section also includes insightful analyses of the results, highlighting the impact of various factors, such as the choice of sampling strategy and dataset characteristics, on the algorithms’ performance. Visualizations in the form of plots and tables are effectively used to aid understanding of the findings. The inclusion of error bars showcases the reliability of the reported results and adds to their overall credibility. The detailed presentation of experimental findings enhances the rigor and reliability of the research. Overall, the results strongly support the claims made in the paper, establishing the practical value of the new algorithms.

Future Directions

#

Future research directions stemming from this bilevel optimization work could explore several promising avenues. Developing more sophisticated sampling strategies beyond the without-replacement methods presented, perhaps incorporating adaptive or variance-reduction techniques, could significantly enhance efficiency. Theoretical analysis could be extended to encompass broader classes of bilevel problems, such as those with non-convex inner or outer objectives, or those involving stochasticity beyond independent sampling. Practical applications to larger-scale, more complex real-world problems are needed to validate the generalizability of these algorithms. Investigating the interplay between example selection and other acceleration techniques like variance reduction or momentum could potentially lead to even faster convergence. Finally, exploring alternative bilevel solution methods entirely, and comparing their performance to this sampling-based approach, would provide valuable insights and could inspire the development of hybrid approaches combining the strengths of multiple methods.

More visual insights

#

More on figures

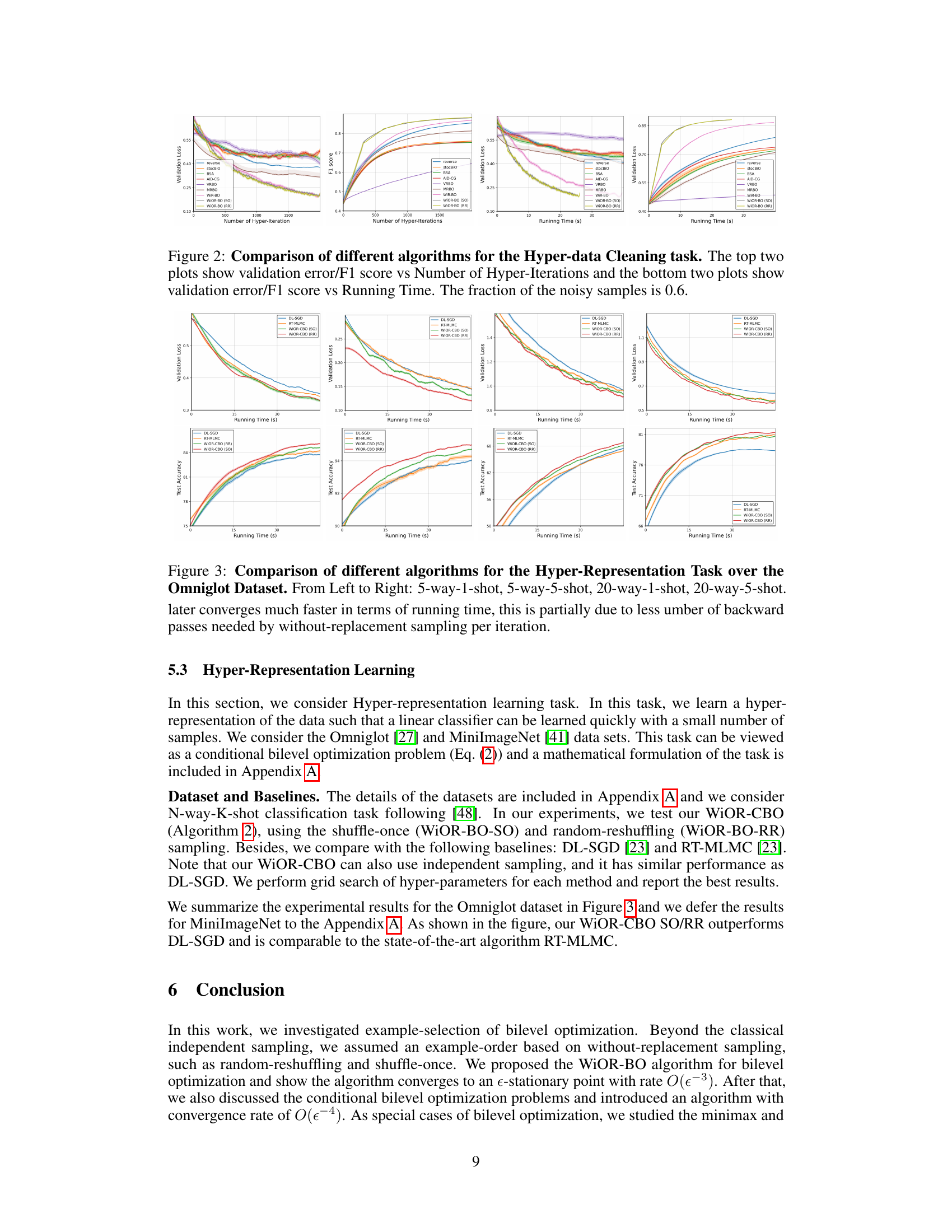
This figure compares the performance of different bilevel optimization algorithms on the hyper-data cleaning task. The top two graphs show validation error and F1 score plotted against the number of hyper-iterations. The bottom two graphs show the same metrics plotted against running time. The experiment uses a dataset with 60% noisy labels.

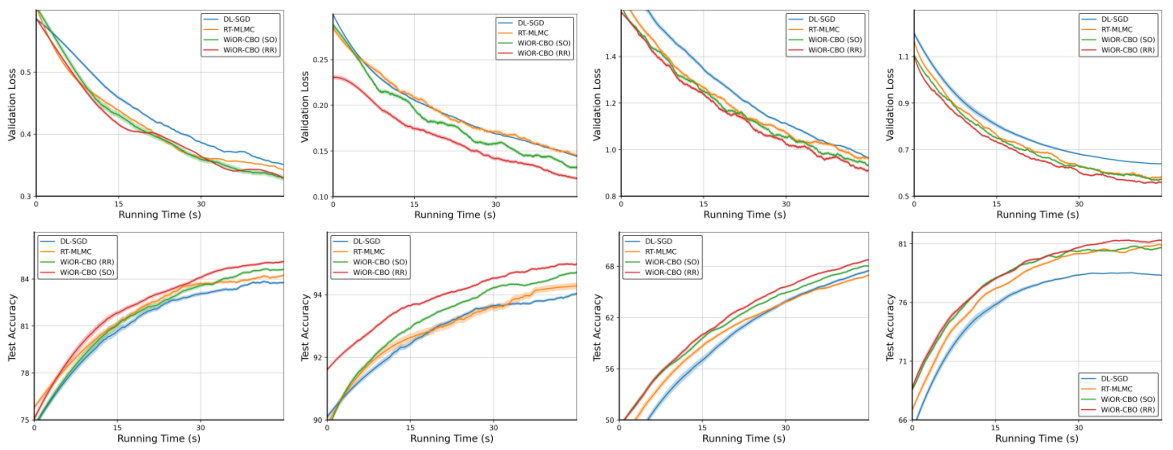
This figure compares the performance of four different algorithms (DL-SGD, RT-MLMC, WiOR-CBO (SO), and WiOR-CBO (RR)) on the Omniglot dataset for few-shot image classification. It shows the validation loss and test accuracy over running time for four different few-shot learning scenarios (5-way 1-shot, 5-way 5-shot, 20-way 1-shot, and 20-way 5-shot). The results demonstrate the effectiveness of the proposed WiOR-CBO algorithm in achieving competitive performance compared to existing state-of-the-art methods.

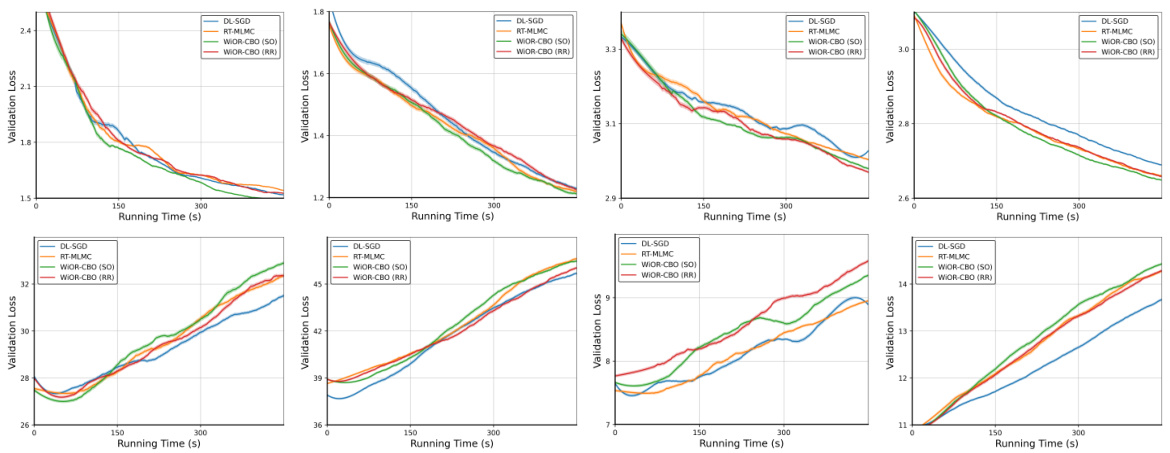
The figure compares different algorithms for hyper-representation learning on the MiniImageNet dataset. Four subplots show the validation loss versus running time for four different experimental settings: 5-way 1-shot, 5-way 5-shot, 20-way 1-shot, and 20-way 5-shot. The algorithms compared include DL-SGD, RT-MLMC, WiOR-CBO (shuffle-once), and WiOR-CBO (random-reshuffling). The results demonstrate the performance of the proposed WiOR-CBO algorithm in comparison to existing methods.

Full paper

#