TL;DR#
Many machine learning tasks assume data is independently and identically distributed (IID). However, real-world data often violates this assumption, resulting in distribution discrepancies between training and test datasets. Measuring this discrepancy is crucial for assessing the generalization ability of a model, especially when test labels are unavailable, a common situation in practice. Existing methods often struggle with this label unavailability, hindering accurate evaluation.
To address this, the authors introduce Importance Divergence (I-Div). I-Div cleverly transfers sampling patterns from the test distribution to the training distribution by estimating density and likelihood ratios, using only the training data. The density ratio is estimated via Kullback-Leibler divergence minimization, informed by the selected hypothesis, while the likelihood ratio is adjusted to reduce generalization error. Experiments across various datasets and complex scenarios validate I-Div’s high accuracy in quantifying distribution discrepancy, confirming its effectiveness for hypothesis applicability evaluation without test labels. This provides a significant advancement in evaluating model generalization capabilities in practical scenarios.
Key Takeaways#
Why does it matter?#
This paper is important because it proposes a novel approach to measure distribution discrepancy in machine learning, which is crucial for evaluating model generalization to unseen data, especially in scenarios where test labels are unavailable. This addresses a significant challenge in real-world applications.
Visual Insights#

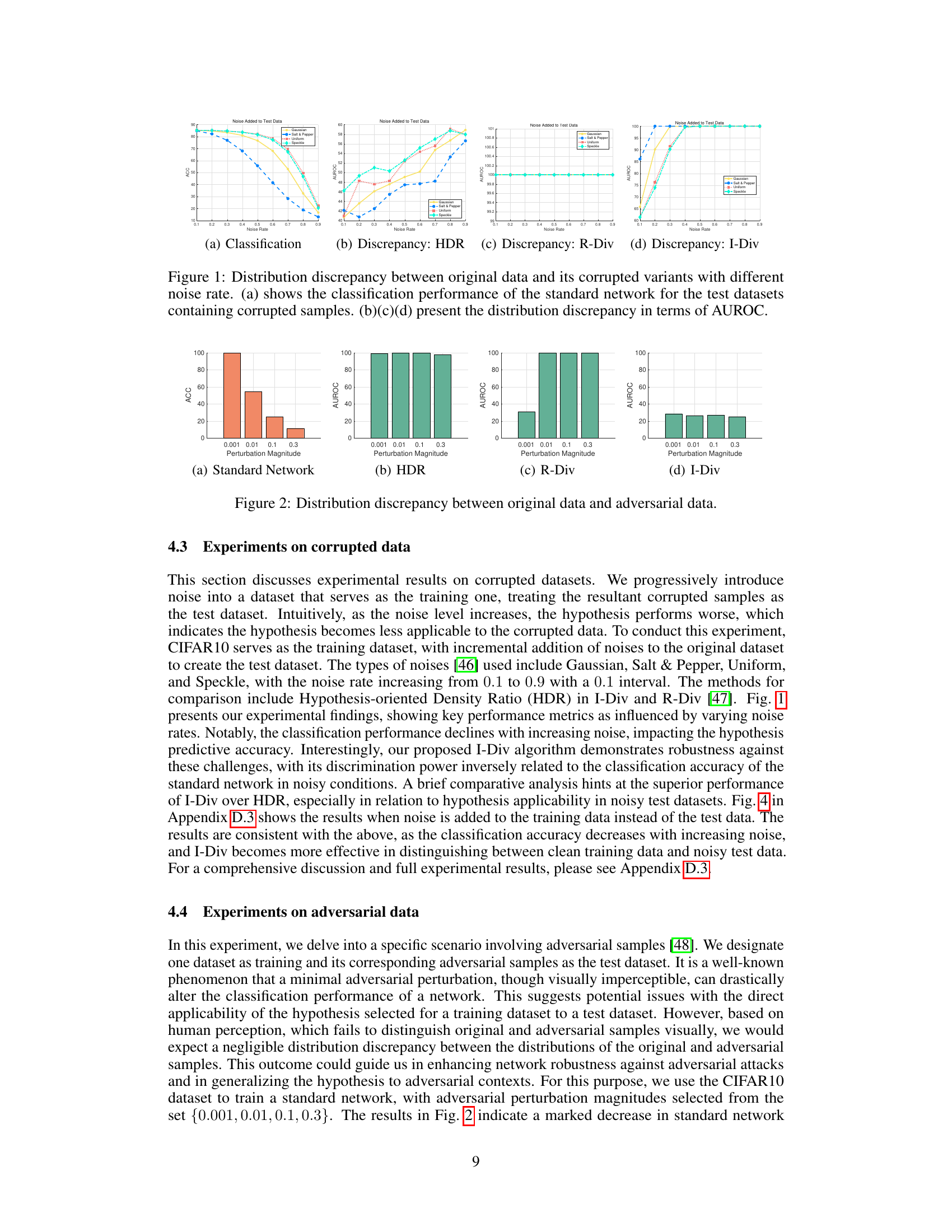
🔼 This figure shows the results of experiments conducted on datasets with varying levels of noise added to the test data. Subfigure (a) displays the classification accuracy of a standard network on these noisy datasets. Subfigures (b), (c), and (d) illustrate the distribution discrepancy (as measured by AUROC) using three different methods: HDR, R-Div, and I-Div. The purpose is to demonstrate the robustness of the I-Div method against noisy data, highlighting its ability to accurately quantify distribution discrepancy even when the test data is corrupted.
read the caption
Figure 1: Distribution discrepancy between original data and its corrupted variants with different noise rate. (a) shows the classification performance of the standard network for the test datasets containing corrupted samples. (b)(c)(d) present the distribution discrepancy in terms of AUROC.

🔼 This table presents the results of evaluating distribution discrepancy using various methods (MSP, NNBD, MMD-D, R-Div, and I-Div) on the CIFAR-10 dataset. Each row represents a different class in CIFAR-10, and the columns show the AUROC (Area Under the Receiver Operating Characteristic Curve) and AUPR (Area Under the Precision-Recall Curve) scores for each method. Higher AUROC and AUPR values indicate better performance in distinguishing between training and test distributions. The results demonstrate I-Div’s superior performance in accurately quantifying distribution discrepancies.
read the caption
Table 1: Distribution discrepancy of different classes in CIFAR10. The larger the values of AUROC and AUPR, the better the performance.
In-depth insights#
I-Div: Core Idea#
The core idea of I-Div centers on quantifying distribution discrepancy between training and test data without requiring test labels. It cleverly leverages importance sampling to transfer sampling patterns from the test to the training distribution, thereby enabling risk estimation on the test set. This is achieved by estimating both density and likelihood ratios. The density ratio, informed by the chosen hypothesis, minimizes Kullback-Leibler divergence between the actual and estimated distributions. Simultaneously, the likelihood ratio is adjusted based on the density ratio to reduce generalization error. I-Div’s innovative approach eliminates the need for test labels, making it highly applicable in scenarios where labeled test data is scarce or unavailable, thus offering a powerful tool for evaluating hypothesis applicability across diverse datasets.
Density Ratio Estimation#
Density ratio estimation is a crucial technique in machine learning, particularly when dealing with covariate shift, where training and test data distributions differ. Accurate density ratio estimation allows for effective transfer learning and domain adaptation by weighting training samples to better reflect the test distribution. Several methods exist, each with strengths and weaknesses. Kernel mean matching (KMM) efficiently aligns distributions, while Kullback-Leibler importance estimation procedure (KLIEP) minimizes KL divergence between the true and estimated distributions. Least-squares importance fitting (LSIF) offers a convex optimization solution. However, the challenge lies in accurately estimating the ratio, especially when high-dimensional or complex data is involved. Deep learning methods have been proposed to address this, but they introduce new challenges around overfitting and model selection. The hypothesis-oriented approach, which tailors the density ratio to a specific hypothesis, presents a particularly interesting avenue for future research, as it directly connects the distribution discrepancy to the model’s performance and generalizability.
Adaptive Likelihood#
The concept of ‘Adaptive Likelihood’ in the context of distribution discrepancy estimation is crucial. It suggests a method for dynamically adjusting the likelihood ratio, a key component in importance sampling techniques used to transfer sampling patterns from the test distribution to the training distribution. This adaptivity is essential because directly estimating the true likelihood ratio is often infeasible due to the lack of labels in test data. By making the likelihood ratio adaptive, the approach attempts to improve the convergence and accuracy of the estimated distribution discrepancy. The adaptivity is likely achieved by tying the likelihood ratio’s estimation to the estimated density ratio, which itself is informed by the hypothesis in question. A hypothesis-oriented approach makes intuitive sense because the relevant distribution discrepancy is inherently dependent on the specific hypothesis under consideration. A well-designed adaptive likelihood ratio would improve the I-Div’s accuracy in quantifying distribution discrepancies, especially in complex real-world scenarios where simple assumptions about the relationship between distributions may not hold. Further research is needed to understand the precise mechanisms by which the likelihood ratio is adapted, and what theoretical guarantees regarding convergence and accuracy are achievable.
Noisy Data Robustness#
The robustness of a model to noisy data is a critical aspect of its real-world applicability. A model’s performance degrades with increased noise, impacting its predictive accuracy. Importance Divergence (I-Div), a novel approach introduced in this paper, demonstrates robustness against noisy data. The distribution discrepancy, as estimated by I-Div, exhibits an inverse relationship with the classification accuracy of a standard network under noise. While other methods such as Hypothesis-oriented Density Ratio (HDR) also show some robustness, I-Div consistently shows superior performance. The key lies in I-Div’s ability to leverage importance sampling, density ratios, and likelihood ratios to quantify the distribution discrepancy without relying on test labels, thus adapting to noisy input more effectively. This makes I-Div a valuable tool for assessing model reliability and generalization in complex, real-world data scenarios where noise is inevitable.
Future Work#
Future work in this area could explore more sophisticated methods for estimating likelihood ratios, addressing the current limitation of I-Div’s reliance on a hypothesis-oriented density ratio. This could involve investigating alternative techniques that do not require class labels in the test data, potentially leveraging techniques like adversarial training or generative models. Furthermore, research into handling more complex data scenarios with high dimensionality or significant noise is warranted. The impact of different loss functions and their influence on the accuracy and robustness of I-Div also merits investigation. Finally, the development of a theoretical framework for understanding the generalization capabilities of I-Div under different distribution shifts would enhance the reliability and application of the proposed methodology. A rigorous empirical evaluation across broader datasets and benchmark tasks, focusing on a deeper investigation of the assumptions of the algorithm, is also crucial for future development.
More visual insights#
More on figures
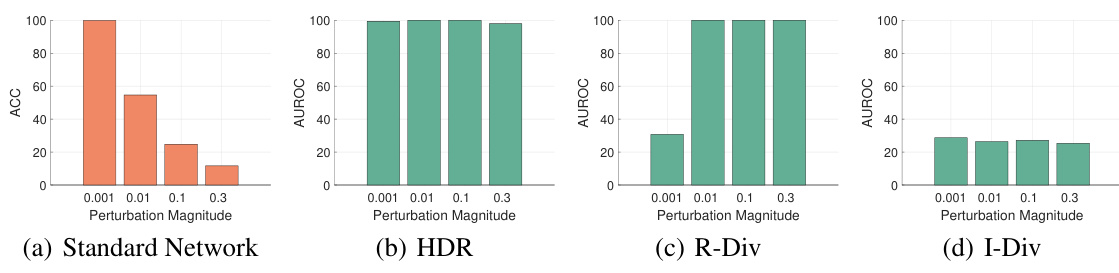
🔼 This figure displays the distribution discrepancy between original data and adversarial examples with varying perturbation magnitudes. It includes four subfigures: (a) Standard Network showing the classification accuracy, (b) HDR (Hypothesis-oriented Density Ratio), (c) R-Div (R-Divergence), and (d) I-Div (Importance Divergence), illustrating the AUROC (Area Under the Receiver Operating Characteristic Curve) for each method. The figure demonstrates the robustness of I-Div against adversarial attacks compared to other methods, maintaining low AUROC values despite a decrease in classification accuracy of the standard network.
read the caption
Figure 2: Distribution discrepancy between original data and adversarial data.

🔼 The figure shows the impact of different sample sizes (M) on the performance of I-Div algorithm. The AUROC and AUPR metrics are plotted against varying sample sizes for different test datasets. Datasets with semantically similar characteristics to the training dataset (CIFAR10) show relatively consistent, low AUROC values, indicating good hypothesis applicability. Conversely, datasets with significant semantic differences show an improvement in performance with increasing sample size, demonstrating the algorithm’s ability to recognize non-transferable knowledge.
read the caption
Figure 3: Effect of different sample sizes.

🔼 This figure shows the results of an experiment where noise was added to the training data, and the resulting distribution discrepancy was measured using different methods. Subfigure (a) displays the classification accuracy of a standard network on the test data with varying noise levels (Gaussian, Salt & Pepper, Uniform, and Speckle noise). Subfigure (b) presents the distribution discrepancy measured using I-Div, showing how well it distinguishes between the clean training data and noisy test data. The experiment demonstrates the robustness of I-Div to noise in training data, as its ability to distinguish between the two distributions remains high even when the classification accuracy is significantly reduced.
read the caption
Figure 4: Distribution discrepancy between original data and its corrupted variants with different noise rate. (a) shows the classification performance of the standard network for the test datasets containing corrupted samples. (b)(c)(d) present the distribution discrepancy in terms of AUROC.
More on tables

🔼 This table presents the results of distribution discrepancy evaluation on domain adaptation datasets, PACS and Office-Home. Each dataset consists of four domains. One domain serves as the training dataset while the remaining three are merged as the test dataset. The table shows the accuracy (ACC) achieved on the source domain (training dataset) along with the AUROC (Area Under the Receiver Operating Characteristic Curve) scores for the different algorithms (MSP, NNBD, MMD-D, R-Div, and I-Div) in evaluating the distribution discrepancy. Higher AUROC values indicate better performance in distinguishing between the training and test distributions.
read the caption
Table 2: Distribution discrepancy of domain adaptation data.
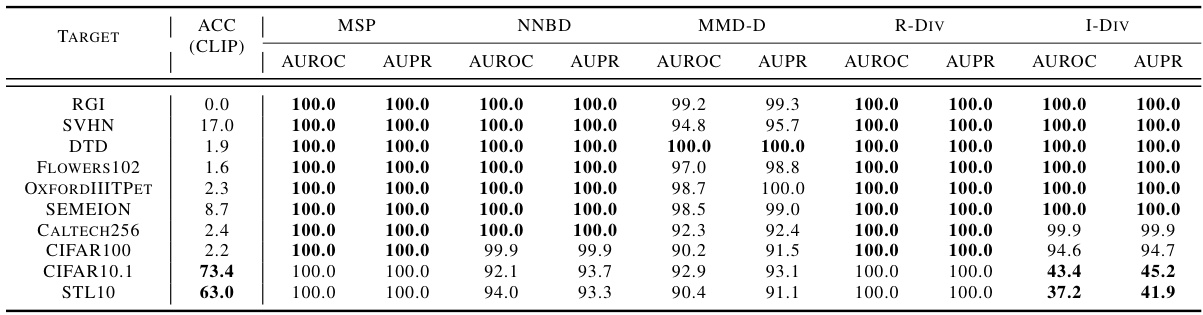
🔼 This table presents the results of evaluating distribution discrepancy for different classes in the CIFAR-10 dataset. Each row represents a different class, where one class is used as the test set and the remaining nine classes comprise the training set. The performance of several algorithms is shown using AUROC (Area Under the Receiver Operating Characteristic Curve) and AUPR (Area Under the Precision-Recall Curve). Higher values indicate better performance in distinguishing between the training and test distributions. The table highlights that I-Div consistently achieves perfect scores (100%) for both AUROC and AUPR metrics across all classes.
read the caption
Table 1: Distribution discrepancy of different classes in CIFAR10. The larger the values of AUROC and AUPR, the better the performance.
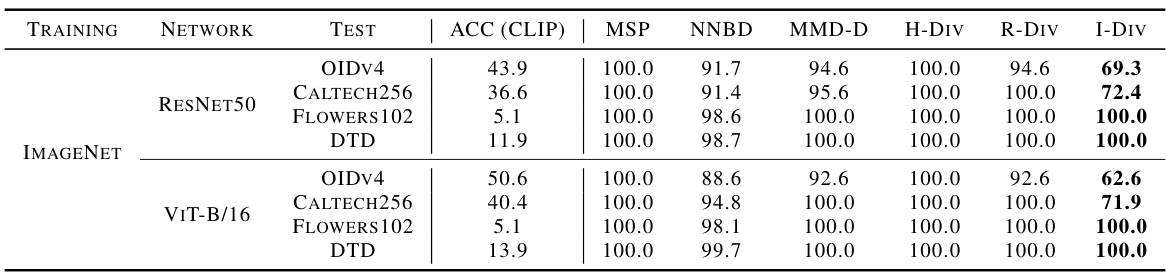
🔼 This table presents the results of experiments evaluating the distribution discrepancy between the ImageNet dataset (used as the training dataset) and four other test datasets: OIDv4, CALTECH256, FLOWERS102, and DTD. Two different network architectures were used: ResNet50 and ViT-B/16. The table shows the accuracy (ACC) achieved by CLIP on the test datasets, and the AUROC and AUPR scores for several methods, including MSP, NNBD, MMD-D, H-Div, R-Div, and I-Div. The results highlight the performance of the I-Div algorithm in capturing the semantic similarity or difference between the training and test datasets.
read the caption
Table 4: Distribution discrepancy between ImageNet and other test datasets.
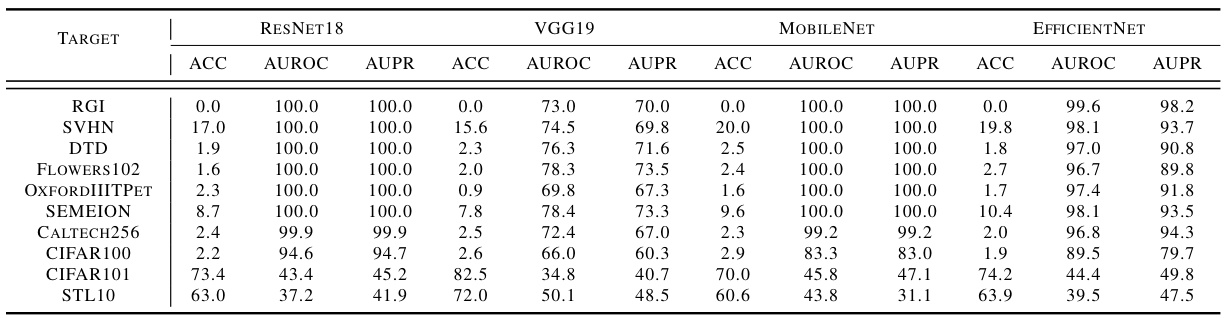
🔼 This table presents the classification accuracy (ACC), Area Under the Receiver Operating Characteristic Curve (AUROC), and Area Under the Precision-Recall Curve (AUPR) for different network architectures (ResNet18, VGG19, MobileNet, EfficientNet) on various datasets (RGI, SVHN, DTD, Flowers102, OxfordIIITPet, SEMEION, Caltech256, CIFAR100, CIFAR101, STL10). The results illustrate the impact of different network architectures on the ability of the I-Div algorithm to differentiate between original data and its adversarial variants.
read the caption
Table 5: Effect of different network architectures.

🔼 This table presents the results of evaluating distribution discrepancy for different digit classes in the SVHN dataset using various methods. The AUROC (Area Under the Receiver Operating Characteristic Curve) and AUPR (Area Under the Precision-Recall Curve) metrics are used to assess the performance of each method in distinguishing between training and test distributions for each digit class. Higher AUROC and AUPR values indicate better performance.
read the caption
Table 6: Distribution discrepancy of different classes in SVHN. The larger the values of AUROC and AUPR, the better the performance.
Full paper#