↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many machine learning models struggle with interpretability, particularly when dealing with high-dimensional data like images. Existing methods often rely on heuristics or pre-trained models, lacking theoretical foundations. This work addresses this by formalizing the concept of learning as identifying a discrete latent hierarchical causal model, where concepts are represented as discrete variables related through a hierarchy. This introduces a novel theoretical perspective and raises important questions regarding model identifiability and how concepts relate to each other.
This paper makes significant contributions by providing sufficient conditions for identifying the proposed hierarchical model from high-dimensional data. These conditions allow for complex causal structures beyond those previously considered in the literature. Furthermore, the researchers provide a novel interpretation of latent diffusion models using this framework, connecting different noise levels to different levels of concept abstraction. This interpretation is empirically supported and provides insights for future model improvements.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with high-dimensional data and latent variable models. It provides novel theoretical insights into learning discrete concepts from complex data, offering a rigorous framework and identifiability conditions. This significantly advances interpretable machine learning and opens new avenues for understanding and improving latent diffusion models.
Visual Insights#
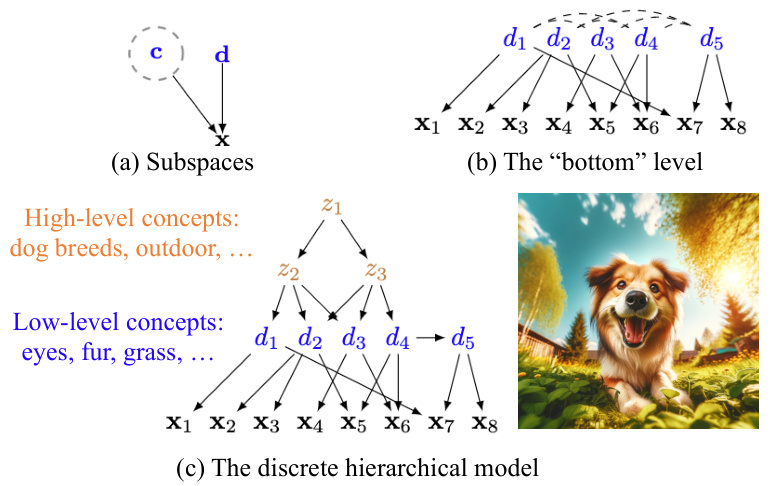
This figure illustrates the hierarchical structure of the proposed latent variable model used for learning discrete concepts from high-dimensional data. Panel (a) shows the subspaces of the model: a continuous subspace representing attributes (c) and a discrete subspace representing concepts (d), which jointly determine the observed variables (x). Panel (b) demonstrates a ‘bottom level’ representation where the discrete concepts (d) directly influence the observed variables (x). Finally, panel (c) shows a full hierarchical model where high-level concepts (z) influence the low-level concepts (d), which in turn influence the observed variables (x). This hierarchical structure captures dependencies between concepts at different levels of abstraction.

This table compares the F1 scores achieved by the proposed method and the baseline method (Dong et al., 2020) on seven different graph structures (Graph 1 to Graph 7). The F1 score is a common metric for evaluating the performance of classification models, and here it measures the accuracy of identifying the hierarchical structure of the model. The high F1 scores obtained by the proposed method indicate its superior performance in recovering the correct graph structures compared to the baseline.
In-depth insights#
Latent Concept ID#
The heading ‘Latent Concept ID’ suggests a research focus on identifying underlying concepts hidden within data. This likely involves techniques from latent variable modeling, aiming to uncover these abstract representations that are not directly observable. The success of such identification hinges on the model’s ability to disentangle these latent concepts from the observed, high-dimensional data. This disentanglement is crucial for interpretability and understanding. The methods employed might include information-theoretic approaches, statistical methods that leverage independence assumptions or graphical modeling to infer causal relationships between latent factors, or a combination of both. A key challenge is the inherent ambiguity in latent variable models, necessitating the development of strategies to address issues of identifiability and to ensure the recovered latent concepts are meaningful and consistent. The effectiveness of the ‘Latent Concept ID’ methods would be judged by their capacity to extract representations that are both interpretable by humans and useful for downstream tasks such as classification, prediction, or generation.
Hierarchical Models#
Hierarchical models offer a powerful framework for representing complex systems by decomposing them into multiple levels of abstraction. In the context of a research paper, a section on hierarchical models would likely explore how these structures can capture dependencies between variables at different levels of granularity. This could involve discussing specific model architectures like Bayesian networks or deep learning models with hierarchical latent variables. The advantages of such models might include improved interpretability, ability to handle high-dimensional data, and better generalization performance. However, challenges in building and applying hierarchical models include the difficulty in specifying the appropriate hierarchical structure, potential identifiability issues, and computational complexity. A comprehensive discussion would delve into these benefits and limitations, perhaps showcasing empirical results on real-world datasets or synthetic data experiments to support the claims made.
LD Model Insights#
The heading ‘LD Model Insights’ suggests an analysis of Latent Diffusion (LD) models, likely focusing on their inner workings and capabilities. A thoughtful exploration would delve into how LD models learn and represent hierarchical concepts. It might investigate whether the different noise levels in LD training correspond to distinct levels of abstraction in concept representation, proposing that higher noise levels capture more abstract, high-level concepts, while lower noise levels retain finer details. The analysis could explore how the model’s architecture, particularly the U-Net encoder, facilitates this hierarchical understanding. Furthermore, a key insight could be the identification of the model’s ability to disentangle concepts, demonstrated through manipulating the latent representation and observing the resulting changes in the generated image. Finally, the exploration may connect the empirical observations to a theoretical framework of concept learning, potentially proposing a causal model that explains the relationships between different levels of concepts, providing a comprehensive understanding of the latent structure generated by LD models and their implications for concept learning.
Sparsity in LD#
The concept of ‘Sparsity in LD’, referring to latent diffusion models, suggests that the learned representations exhibit a sparse structure. This means that only a small subset of the model’s parameters significantly contribute to generating each specific feature or concept within an image. This sparsity is crucial for interpretability, as it allows for easier identification and understanding of the learned features. The sparse structure also promotes efficiency and generalization, by reducing model complexity and preventing overfitting. Higher-level concepts, often encoded in the later stages of the diffusion process, are likely to be represented more sparsely than lower-level details. This hierarchical sparsity reflects the inherent structure of information in visual data, where high-level concepts summarize many lower-level details. Analyzing and utilizing this sparsity is key to improving the interpretability of latent diffusion models and enhancing their efficiency and performance.
Future Directions#
Future research could explore several promising avenues. Extending the theoretical framework to encompass more complex causal structures beyond the hierarchical model presented is crucial. This might involve incorporating feedback loops or more intricate dependencies between latent variables. Developing efficient algorithms for identifying these complex models is a key computational challenge. The current algorithms, while theoretically sound, may struggle with very high-dimensional data or a large number of latent variables. Bridging the gap between theoretical results and practical applications is vital. This involves further investigation into applying the concepts to real-world problems, focusing on datasets with nuanced structural properties, and evaluating performance against existing methods. Investigating the implications of the theoretical results for various machine learning models such as latent diffusion models could uncover hidden relationships and possibly lead to improvements in model design and interpretability. Finally, exploring the robustness of the proposed model to noisy or incomplete data is another important direction, thereby enhancing its practicality and applicability in various real-world settings.
More visual insights#
More on figures
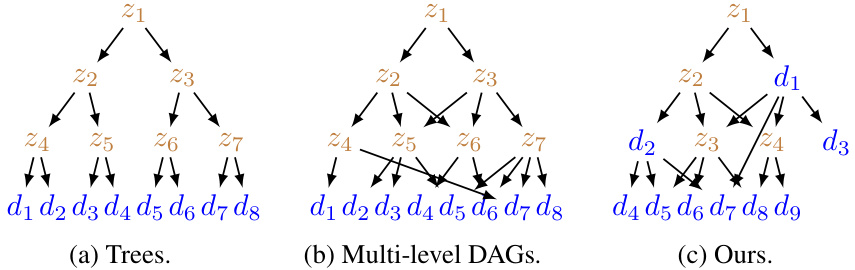
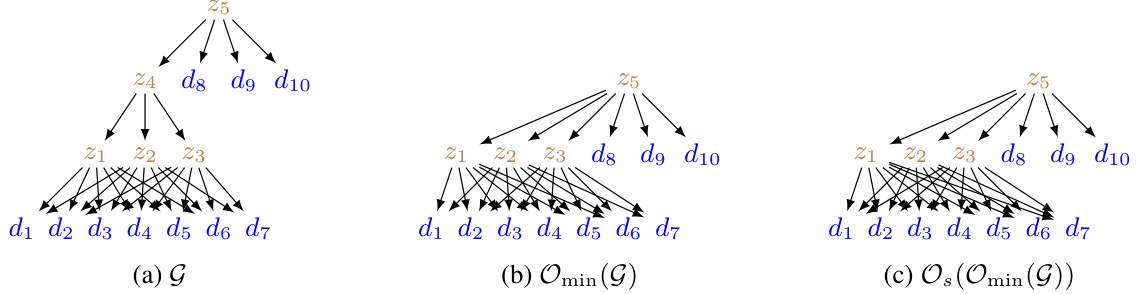
This figure compares three different types of graphical models used to represent hierarchical relationships between variables. (a) shows a tree structure, where there is only one path between any two nodes. (b) shows a multi-level DAG, where nodes are arranged in levels and connections exist only between adjacent levels. (c) shows the model proposed in the paper, which is more flexible than the previous models. It allows multiple paths between variables, regardless of the level they are in, and it can include non-leaf nodes in the graph. This increased flexibility allows the model to capture more complex relationships in the data.
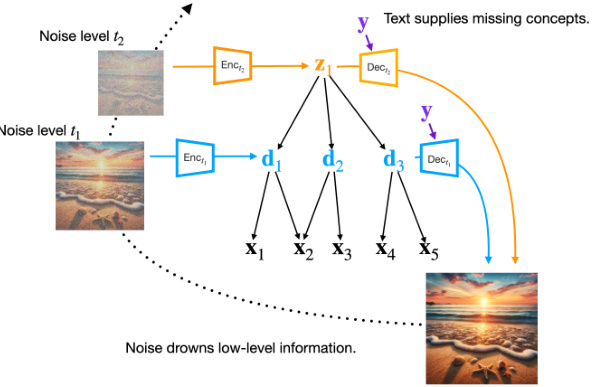
This figure illustrates how a latent diffusion model can be interpreted through the lens of a hierarchical concept model. Different noise levels in the diffusion process correspond to different hierarchical levels in the concept model. The encoder of the diffusion model at a particular noise level extracts a representation that corresponds to a particular level of concepts. At higher noise levels, low-level concepts are lost, resulting in a representation that focuses on higher-level, more abstract concepts. The decoder reconstructs the original representation using the compressed representation and optional text information.
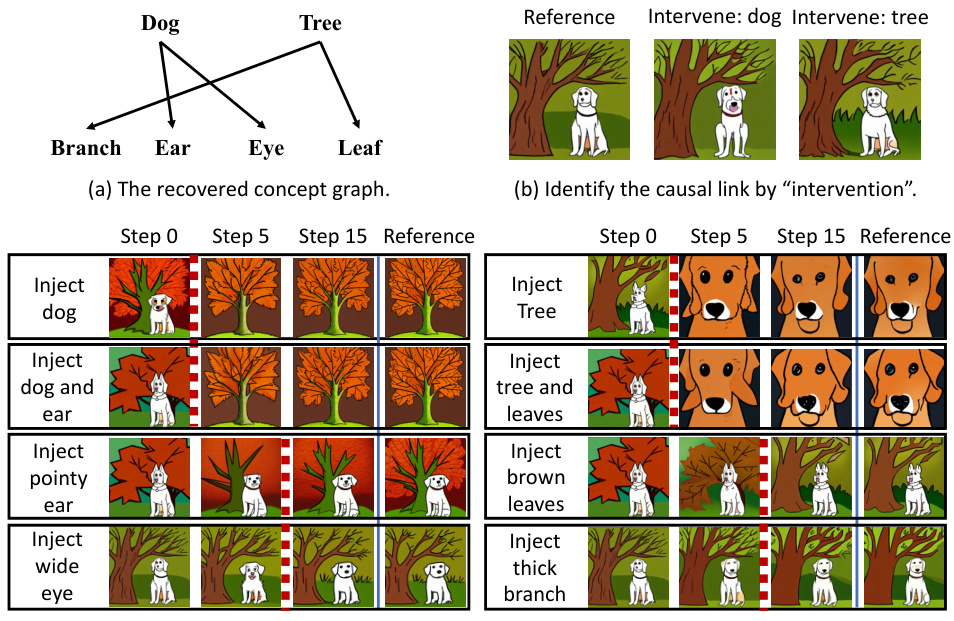
This figure shows how the authors recovered concepts and their relationships from a Latent Diffusion model. Part (a) displays the resulting hierarchical graph of concepts. Part (b) demonstrates how interventions on higher-level concepts (e.g., adding ‘dog’) affect lower-level concepts (’eyes’, ’ears’), revealing causal relationships. Part (c) illustrates how the timing of concept injection during the diffusion process reveals the hierarchical order of concepts (higher-level concepts injected earlier).

This figure shows how modifying the diffusion model’s representation at different times (early vs late) affects the generated image’s semantics. Early modifications result in global changes (e.g., breed, species, gender), while later changes produce more localized effects (e.g., accessories, minor features). This visually demonstrates the hierarchical structure of concepts within the latent space, where early stages represent higher-level concepts and later stages represent lower-level details. The results support the paper’s interpretation of latent diffusion models as hierarchical concept learners.
This figure illustrates the concept of a hierarchical model with continuous and discrete latent variables. Panel (a) shows the overall model structure, illustrating continuous variables ‘c’ and discrete variables ’d’. Panel (b) focuses on the discrete latent variables ’d’ as the leaves of the hierarchy. The dashed lines in (b) represent potential statistical dependence between the concepts represented by the discrete variables, which are further explained by a higher-level concept in (c), showing how concepts are hierarchically related.

This figure illustrates the data generating process and the model used in the paper. Panel (a) shows that the high-dimensional continuous observed variables (x) are generated from discrete latent variables (d) and continuous latent variables (c). Panel (b) zooms in to the ‘bottom level’ of the model, showing the relationship between the discrete latent variables and the continuous observed variables. Panel (c) shows a hierarchical model composed of both high-level and low-level discrete latent variables. The hierarchical model describes the dependence among different abstraction levels of concepts.

This figure illustrates three different graphical representations of latent hierarchical models. (a) shows the general structure, with continuous and discrete subspaces that are parents to the observed variables x. (b) zooms in on the ‘bottom’ level to emphasize the relationship between discrete latent variables d and the continuous observed variables x. Finally, (c) shows a full hierarchical model where the discrete variables are connected via higher-level concepts, allowing for complex dependencies among the concepts.
This figure compares three different types of graphical models representing hierarchical relationships among variables: trees, multi-level directed acyclic graphs (DAGs), and the model proposed in the paper. Trees allow only one path between any two variables, while multi-level DAGs are more structured and restrict edges to exist only between adjacent levels. The authors’ model is more flexible, enabling multiple paths between variables and allowing non-leaf nodes (observed variables) at any level in the hierarchy.
This figure compares three types of graphical models for representing latent variables: trees, multi-level directed acyclic graphs (DAGs), and the model proposed in the paper. Trees only allow one path between any two nodes, which is too restrictive. Multi-level DAGs stratify variables into levels, with connections only between adjacent levels, which is also restrictive. The proposed model offers greater flexibility in the relationships between variables, allowing for multiple paths and non-leaf observed variables.

This figure visualizes the attention sparsity of a latent diffusion model over diffusion steps and specific attention patterns. The results show that the sparsity increases as the generative process progresses, which reflects that the connectivity between the hierarchical level and the bottom concept level becomes sparse and more local as we march down the hierarchical structure. This observation supports the theory proposed in the paper.

This figure demonstrates the hierarchical nature of concepts in a latent diffusion model. Injecting high-level concepts early in the generation process, followed by low-level concepts, results in images that faithfully reflect all injected concepts. Reversing this order leads to incomplete or inaccurate image generation. This supports the hierarchical model’s structure, with higher-level concepts influencing lower-level ones.

This figure shows the results of an experiment where different ranks of LoRA (Low-Rank Adaptation) were used to modify images with specific concepts. The experiment demonstrates that the appropriate rank of LoRA is crucial for effectively and faithfully modifying images with the desired concept without introducing unwanted artifacts. Higher ranks, while potentially offering more detail, may introduce unwanted alterations or distortions.
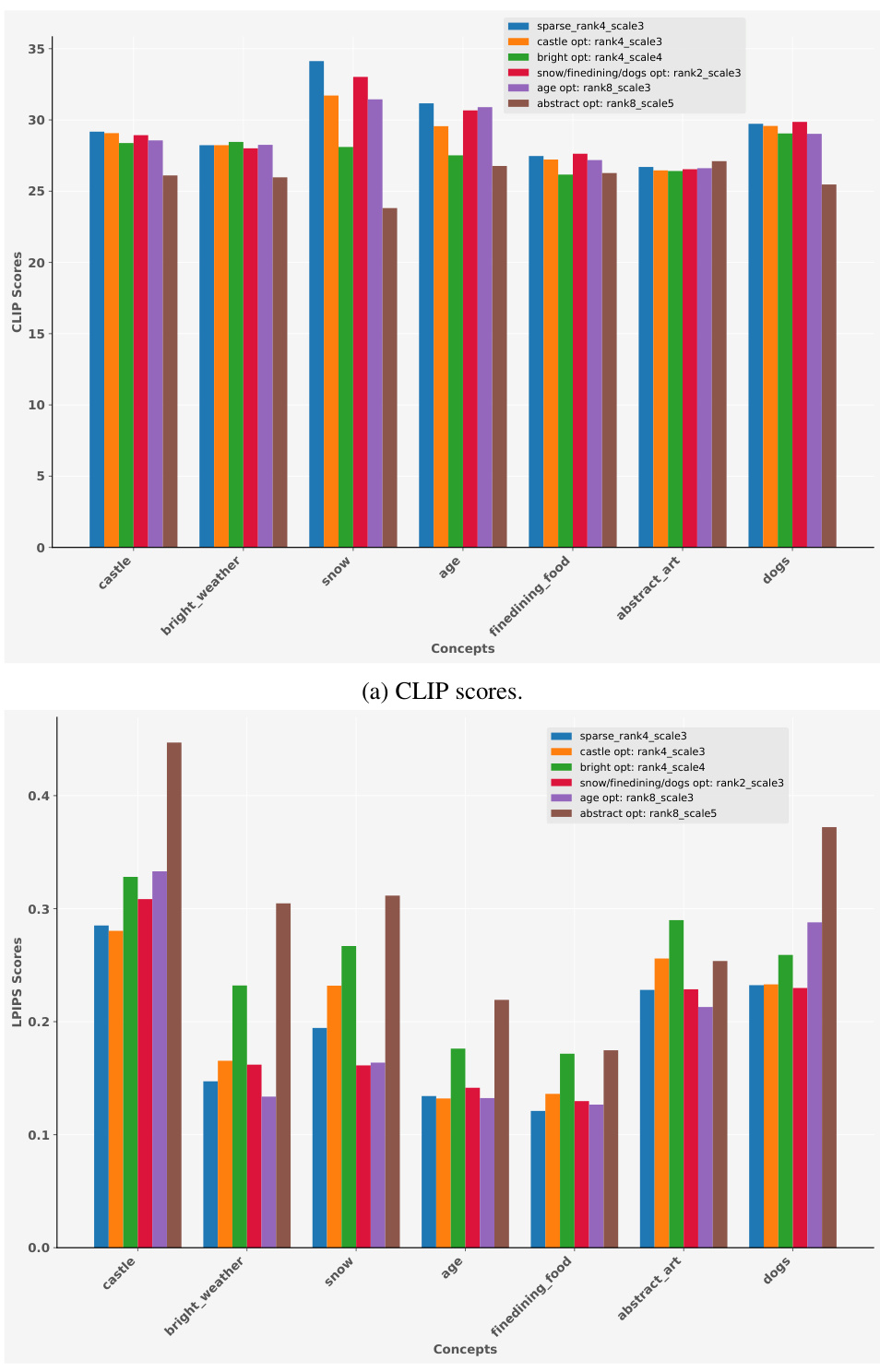
This figure shows the results of CLIP and LPIPS evaluations for different concepts using various rank settings. It compares the performance of a sparse approach with an optimal fixed rank approach, highlighting the effectiveness of adaptive rank selection in achieving high semantic alignment with minimal image alterations.

This figure shows experiments on injecting concepts into a diffusion model at different time steps. The top row shows that injecting high-level concepts first and then low-level concepts produces images that successfully integrate all concepts. The bottom row reverses the order, showing that injecting low-level concepts first results in failure to include the high-level concept in the generated image. This demonstrates the hierarchical relationship between concepts in the model.

This figure provides additional examples to illustrate the concept of editing latent representations at different time steps in latent diffusion models. The top two rows show changes in image generation when manipulating image representations at early versus late diffusion steps. The changes induced by manipulating early steps correspond to shifting global concepts, while changes in later steps correspond to finer-grained changes. The bottom two rows demonstrate similar effects for different image types.
Full paper#



















