↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
The research tackles the challenge of out-of-distribution generalization in machine learning, where models trained on one dataset may not perform well on another. This is a significant problem, as real-world data often exhibit distribution shifts (covariate and concept shifts). Existing calibration methods, while useful, are often insufficient to handle such shifts. The paper highlights that accurate prediction under distribution shift can be addressed by multicalibration which ensures a predictor is accurate across various overlapping groups.
The paper introduces a new model-agnostic optimization framework that extends multicalibration to consider covariates and labels jointly. This leads to a novel post-processing algorithm, MC-Pseudolabel. This algorithm leverages a linear structure within the grouping function class, enabling efficient hyperparameter tuning and achieving superior performance in real-world datasets with distribution shifts. The findings demonstrate MC-Pseudolabel’s ability to improve robustness and generalization in challenging scenarios, offering a practical and effective approach to out-of-distribution generalization problems.
Key Takeaways#
Why does it matter?#
This paper is crucial because it bridges multicalibration and out-of-distribution generalization, two significant challenges in machine learning. By establishing a model-agnostic framework and proposing a novel algorithm, MC-Pseudolabel, it offers practical solutions to improve model robustness and generalization. This work opens doors for further research in robust learning techniques and their applications to real-world problems with distribution shift.
Visual Insights#
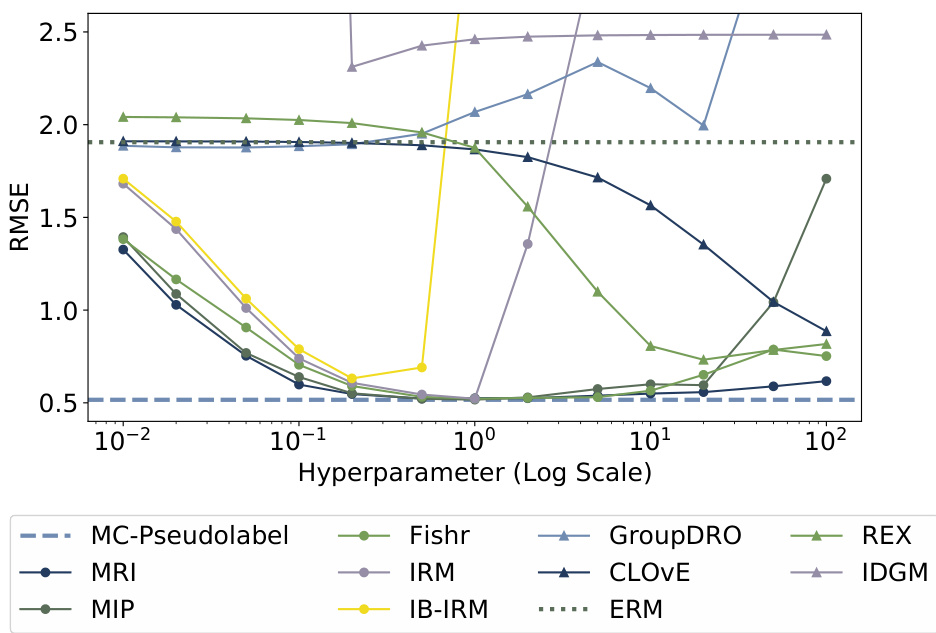
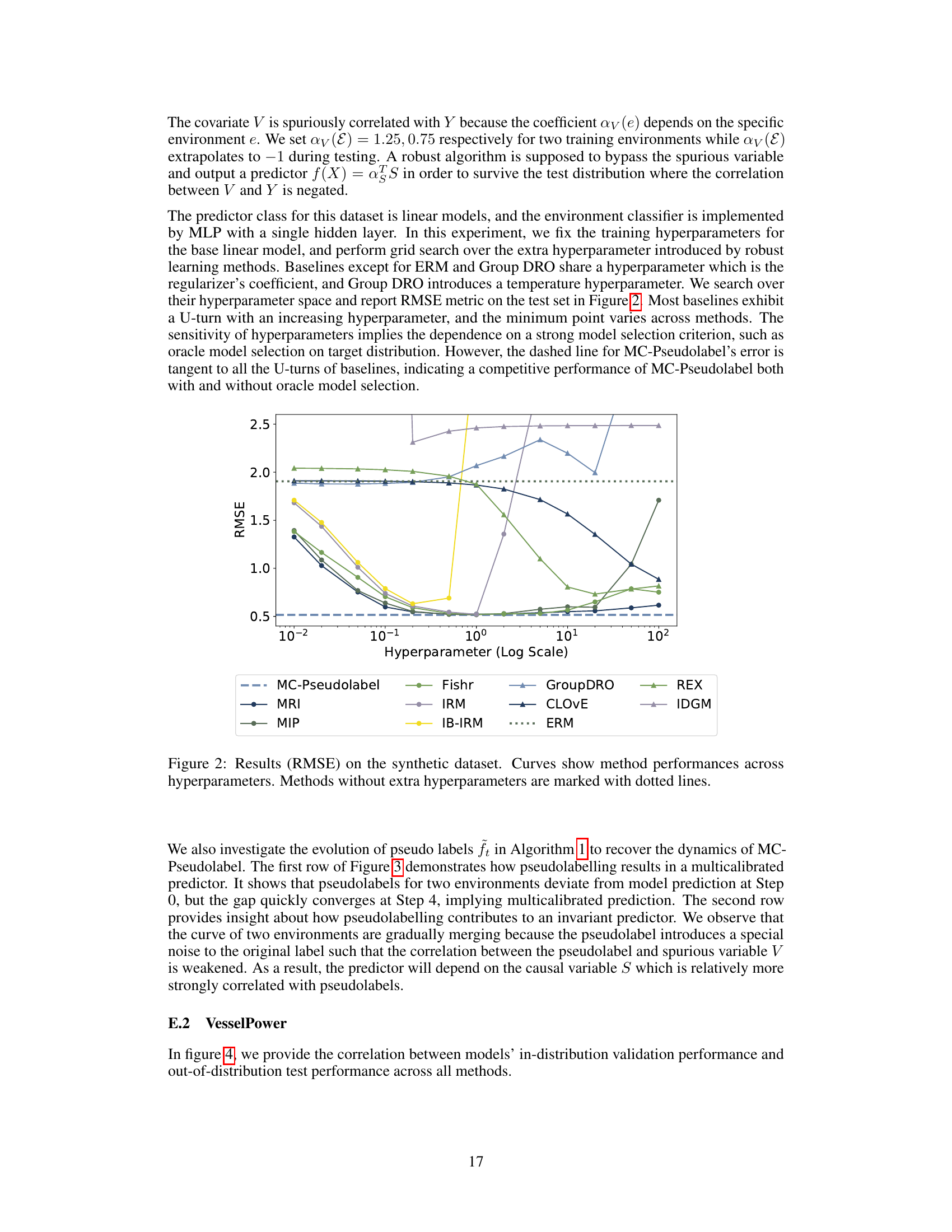
This figure displays the RMSE (Root Mean Squared Error) results from various robust learning methods on a synthetic dataset, designed to evaluate their performance under concept shift. The x-axis represents the hyperparameter values (on a logarithmic scale), while the y-axis displays the corresponding RMSE. Each line represents a different method, demonstrating how their performance changes with varying hyperparameter settings. The dotted lines indicate methods without additional hyperparameters, allowing for a comparison against methods with added hyperparameter tuning.
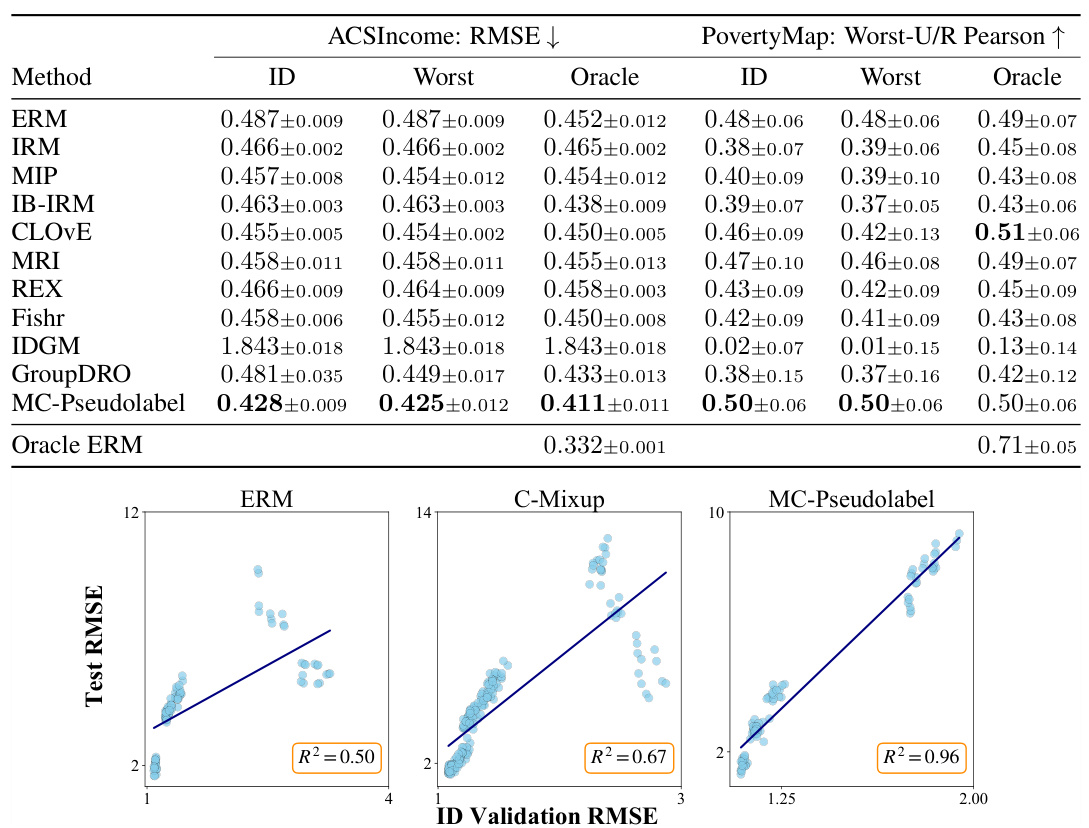
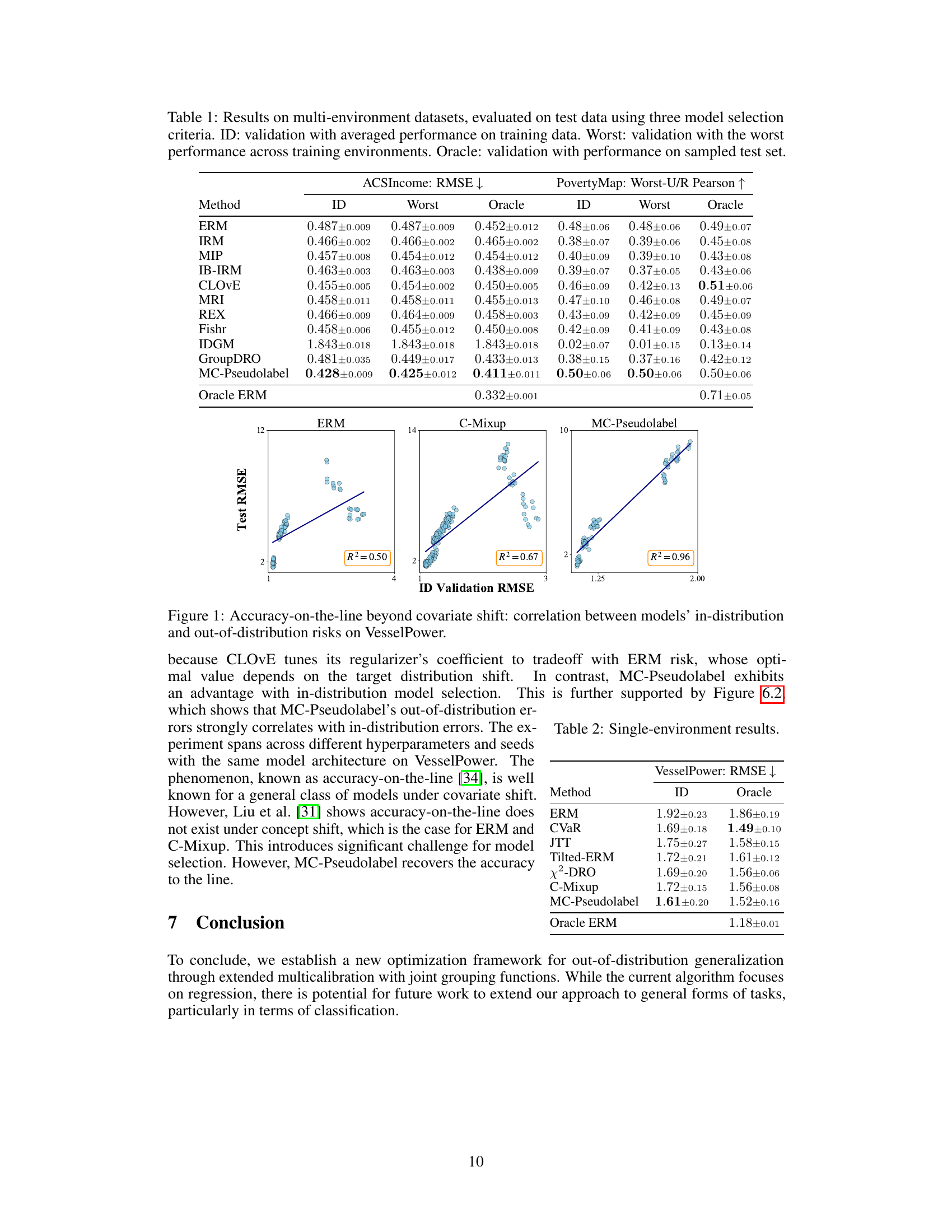
This table presents the results of the experiments conducted on multi-environment datasets. Three different model selection criteria were used for evaluation: in-distribution (ID) validation, worst-environment (Worst) validation, and oracle validation. The table compares the performance (RMSE for ACSIncome and Worst-U/R Pearson for PovertyMap) of various methods, including MC-Pseudolabel and several baselines, across these criteria. The results highlight the performance differences between the models under different evaluation scenarios, showing which models are more robust to distribution shifts.
In-depth insights#
Multicalibration’s Bridge#
The concept of “Multicalibration’s Bridge” in the context of the provided research paper likely refers to the connection established between multicalibration and out-of-distribution generalization. The paper likely demonstrates how multicalibration, a fairness-focused calibration criterion, can improve a model’s robustness when faced with data from different distributions than those seen during training. This bridge is likely built by extending the traditional notion of multicalibration to consider joint grouping functions that depend on both covariates and labels. This allows the framework to handle concept drift scenarios, which go beyond the typical covariate shift addressed in prior works. The key insight is that by enforcing calibration across multiple overlapping groups defined by these joint functions, the model becomes invariant to certain distributional shifts, thus improving its out-of-distribution performance. This connection likely involves showing an equivalence between extended multicalibration and invariance, a key objective in robust machine learning. The paper might introduce an algorithm that leverages this connection, potentially by post-processing a pre-trained model to achieve extended multicalibration, thereby achieving improved generalization capabilities. Algorithm MC-Pseudolabel might be the suggested approach for this purpose.
Joint Grouping#
The concept of “Joint Grouping” in the context of the provided research paper appears to be a novel approach to address the limitations of traditional multicalibration methods. Instead of considering only covariates (input features) for defining subgroups as in standard multicalibration, joint grouping incorporates both covariates and labels (outcomes). This extension is crucial because it enables the model to learn the relationships between inputs and outputs in a more nuanced way, especially under concept shift. Concept drift, which involves changes in the relationship between inputs and outputs, is a common challenge in real-world scenarios that traditional covariate-based multicalibration approaches struggle with. By jointly considering covariates and labels, this technique is more robust to changes in the underlying data generating process. This method moves beyond merely addressing covariate shift, to deal with concept shift, by focusing on the invariance of the prediction to shifts in the conditional distribution of outcomes, given features. This results in improved out-of-distribution generalization, which is a critical aspect for developing robust and reliable machine learning models in the real world.
MC-Pseudolabel Alg.#
The proposed MC-PseudoLabel algorithm presents a novel post-processing approach for enhancing model robustness and out-of-distribution generalization. It leverages the concept of extended multicalibration, incorporating grouping functions that jointly consider covariates and labels. This addresses shortcomings of traditional multicalibration, which primarily focuses on covariate shift. By iteratively refining predictions using pseudo-labels generated by these joint grouping functions, MC-PseudoLabel achieves both extended multicalibration and invariance, a key property for robustness under concept shift. Lightweight in terms of hyperparameters, the algorithm’s iterative supervised regression steps provide an efficient optimization process, unlike computationally expensive multi-objective optimization methods. Its convergence properties are theoretically analyzed under specific conditions, further strengthening its reliability. The experimental results highlight MC-PseudoLabel’s improved performance on real-world datasets with concept shift, surpassing several state-of-the-art methods in terms of both in-distribution and out-of-distribution generalization.
Beyond Covariate Shift#
The concept of “Beyond Covariate Shift” in the context of this research paper implies addressing distribution shifts that extend beyond simple covariate shifts. Covariate shift assumes the relationship between features (X) and labels (Y) remains consistent, only the distribution of features changes. However, “Beyond Covariate Shift” acknowledges that in real-world scenarios, this assumption often breaks down. Concept shift, where the relationship between X and Y itself changes, becomes crucial. The paper likely proposes methods that address this more complex scenario, potentially incorporating labels into the model’s understanding of distribution shift. This could involve techniques that model the joint distribution P(X,Y) explicitly or implicitly, allowing the model to adapt to changes in the conditional distribution P(Y|X) as well as P(X). The authors likely showcase how this enhanced robustness leads to improved out-of-distribution generalization, going beyond the limitations of methods solely designed for covariate shift. This is a significant advancement because addressing concept drift is a considerably more challenging problem, with implications for model reliability in diverse real-world applications.
Future Work#
Future research directions stemming from this work could explore extensions to other loss functions beyond squared error, investigating the robustness and theoretical properties of extended multicalibration under more general settings. The current model focuses on regression tasks; therefore, adapting the algorithms and theory to classification problems is another crucial area. Furthermore, a deeper investigation into the structural properties of the maximal grouping function class and more efficient ways to design this class are needed. Finally, exploring the practical impact and trade-offs of different design choices for grouping functions, particularly under scenarios with limited labeled data, would significantly improve the algorithm’s usability and applicability. The development of more efficient computational methods to reduce the algorithm’s runtime, potentially using parallelization techniques and specialized hardware would also be highly beneficial.
More visual insights#
More on figures
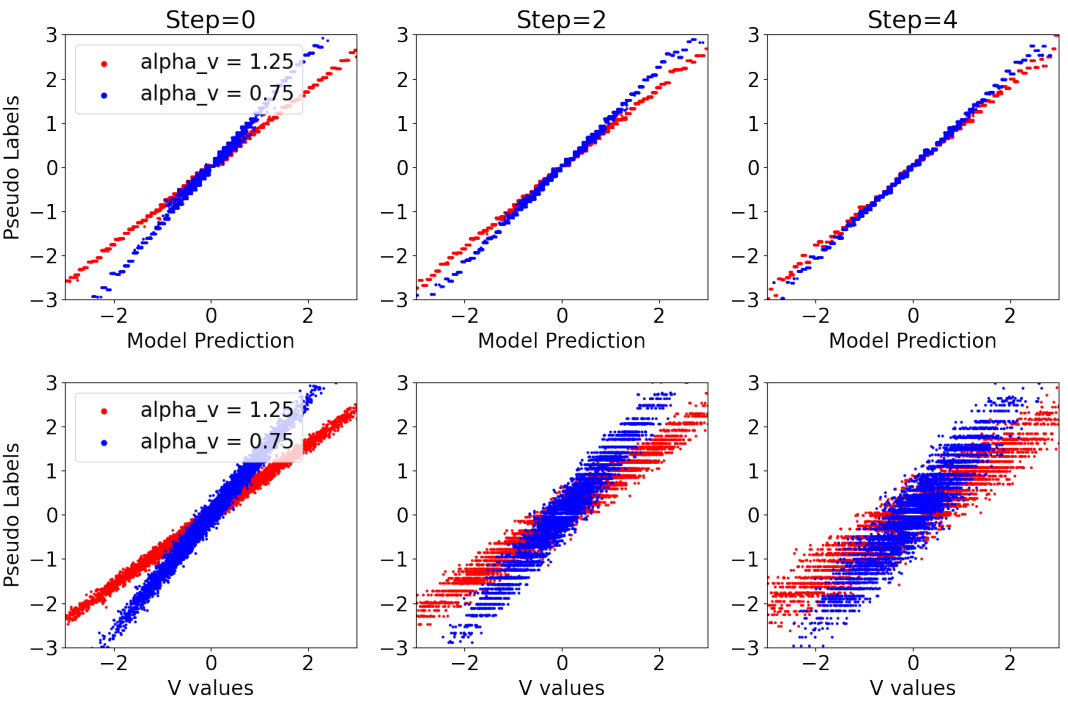
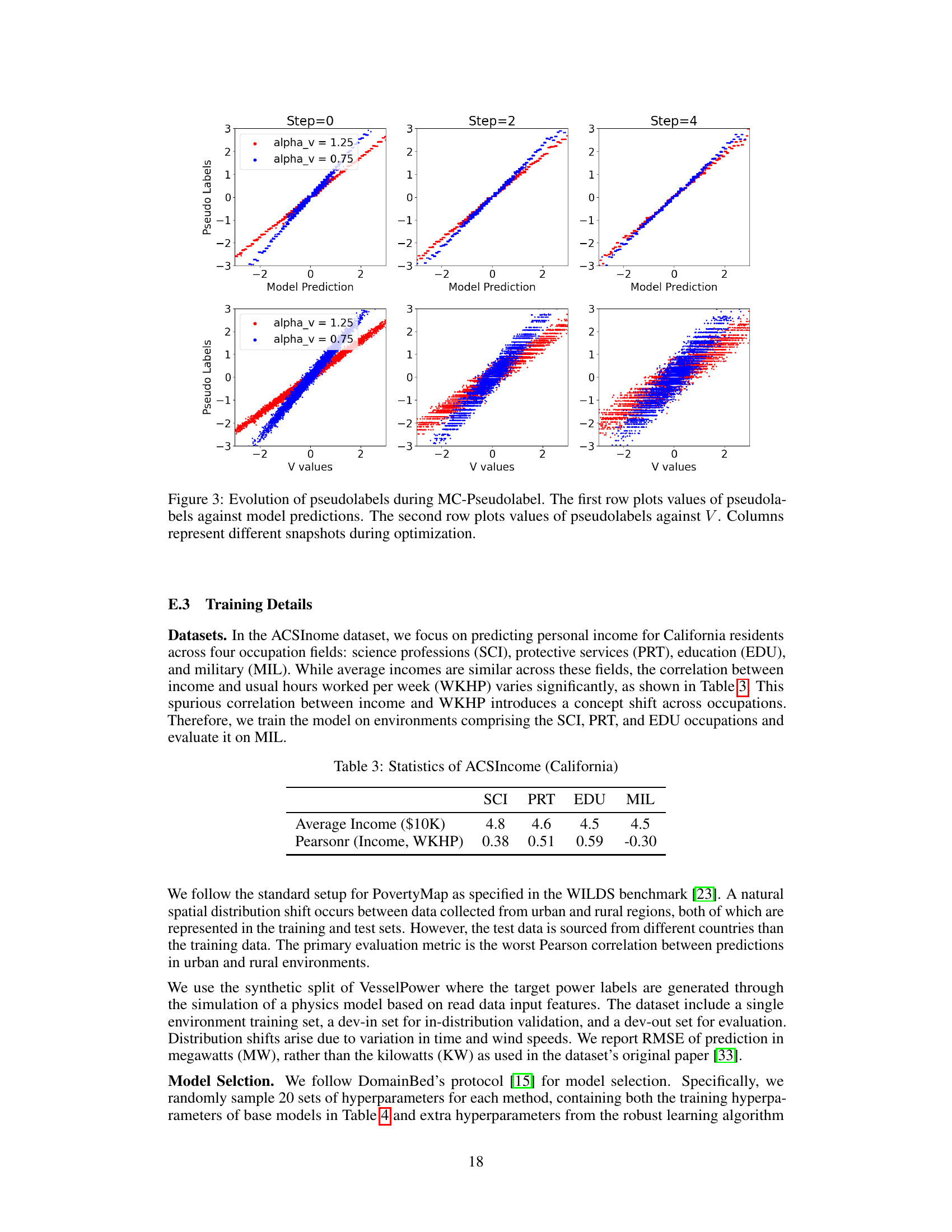
This figure visualizes the iterative process of the MC-PseudoLabel algorithm. The top row shows how the algorithm refines pseudolabels (generated by grouping functions) in relation to the model’s predictions across different iterations (Step 0, Step 2, Step 4). The bottom row shows the same pseudolabels against the spurious variable ‘V’. The converging plots in both rows demonstrate how the algorithm iteratively adjusts predictions to achieve multicalibration and invariance, reducing the influence of spurious correlations.
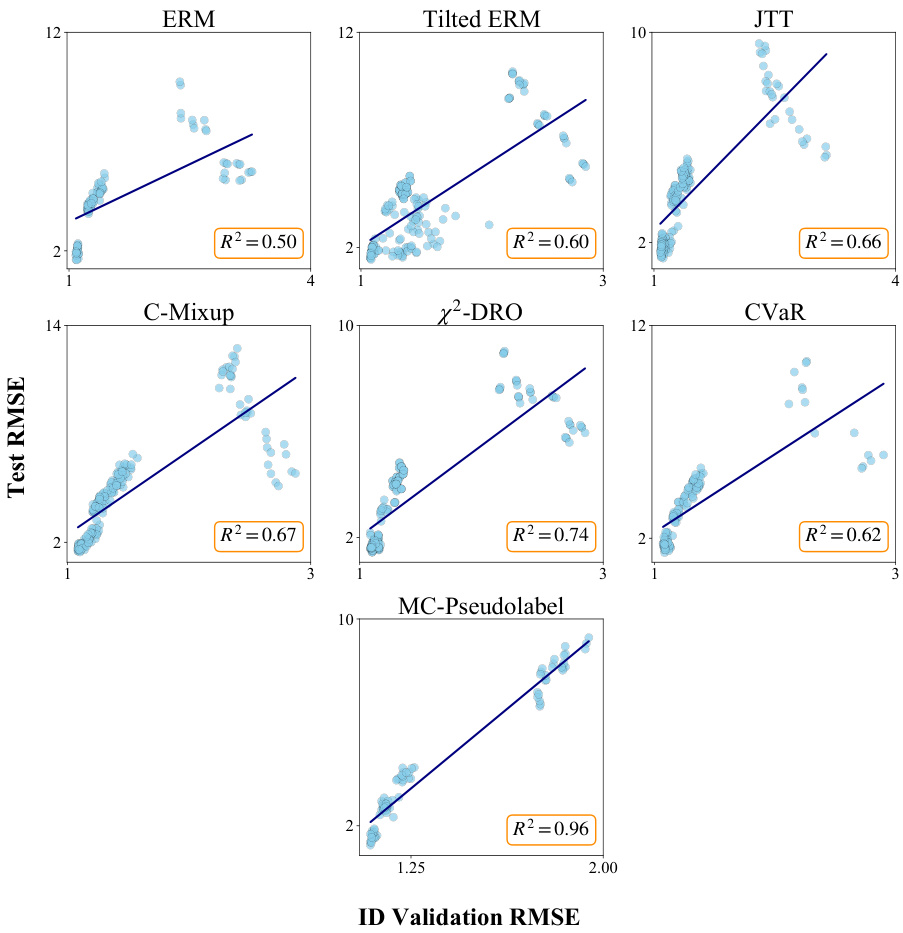
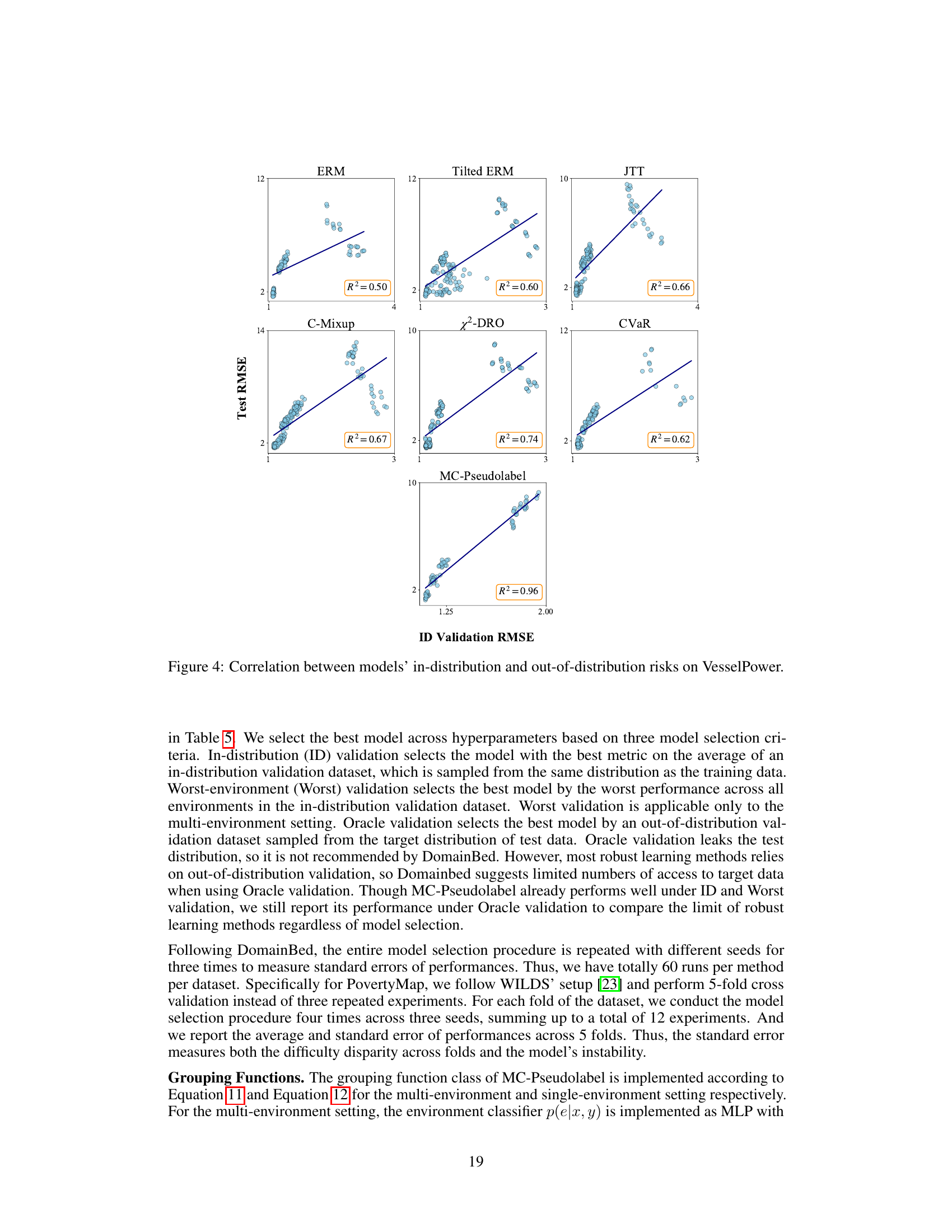
This figure displays the relationship between a model’s in-distribution performance (measured by ID validation RMSE) and its out-of-distribution performance (measured by test RMSE) on the VesselPower dataset. The strong positive correlation (R²=0.96 for MC-Pseudolabel) indicates that the method’s in-distribution performance is a good predictor of its out-of-distribution performance, a phenomenon known as ‘accuracy-on-the-line’. This contrasts with other methods which show weaker correlations, suggesting that MC-Pseudolabel generalizes better to out-of-distribution data.
More on tables
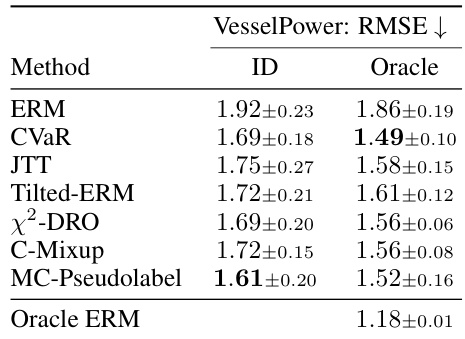
This table presents the results of experiments conducted in a single-environment setting, where algorithms are trained on a single source distribution and tested on a target dataset with distribution shift. The table shows the performance of different methods, including the proposed MC-Pseudolabel algorithm and several baselines, using the ID (in-distribution) and Oracle (out-of-distribution) validation metrics. The performance is measured using RMSE (Root Mean Squared Error), a common metric for regression tasks.

This table presents the results of experiments conducted on three multi-environment datasets (ACSIncome, PovertyMap, VesselPower). Three model selection criteria were used to evaluate the performance of different algorithms: In-distribution (ID) validation using the average performance across training data; Worst-environment validation using the worst performance across all training environments; and Oracle validation which uses performance on a sampled test set. The table shows the performance (RMSE for ACSIncome and VesselPower, Worst-U/R Pearson for PovertyMap) for each algorithm under each selection criterion. The lower RMSE and higher Worst-U/R Pearson values indicate better performance.

This table lists the hyperparameters used for the model architectures in the experiments. It shows the architecture (linear model, MLP, and Resnet18-MS), hidden layer dimensions, optimizer (Adam), weight decay, loss function (MSE), learning rate, and batch size for each dataset (Simulation, ACSIncome, VesselPower, PovertyMap). Note that the learning rate and batch size for ResNet18-MS follow the settings used in the WILDS benchmark.

This table presents the results of experiments conducted on three multi-environment datasets (ACSIncome, PovertyMap, and VesselPower). Three different model selection criteria were used to evaluate the performance of various methods: In-distribution (ID) validation, Worst-case (Worst) validation across training environments, and Oracle validation. The table compares the performance (RMSE for ACSIncome, Worst-U/R Pearson for PovertyMap) of MC-PseudoLabel against several baseline methods under each criterion.
Full paper#