↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Causal discovery, crucial for understanding relationships between variables, faces challenges in scaling up to large datasets, especially for permutation-based methods used in linear Gaussian acyclic models (LiGAMs). Existing methods struggle with the high computational complexity of constructing and searching causal orderings. This limits their applicability to real-world problems with numerous variables.
The proposed QWO method significantly addresses these scalability issues. It introduces a novel algorithm that efficiently computes the optimal causal graph for a given permutation. QWO boasts an O(n²) speedup over existing methods, making it highly scalable. Furthermore, QWO is theoretically sound and easily integrates with existing search strategies, enhancing their performance and broadening the range of problems solvable by permutation-based approaches. The method’s effectiveness is demonstrated through experiments, confirming its scalability and accuracy in various scenarios.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in causal discovery because it offers a scalable solution to a long-standing computational challenge. The O(n²) speedup achieved by QWO is significant, enabling the analysis of larger and more complex datasets. This opens new avenues for applying permutation-based methods in diverse fields and advances the state-of-the-art in causal inference.
Visual Insights#

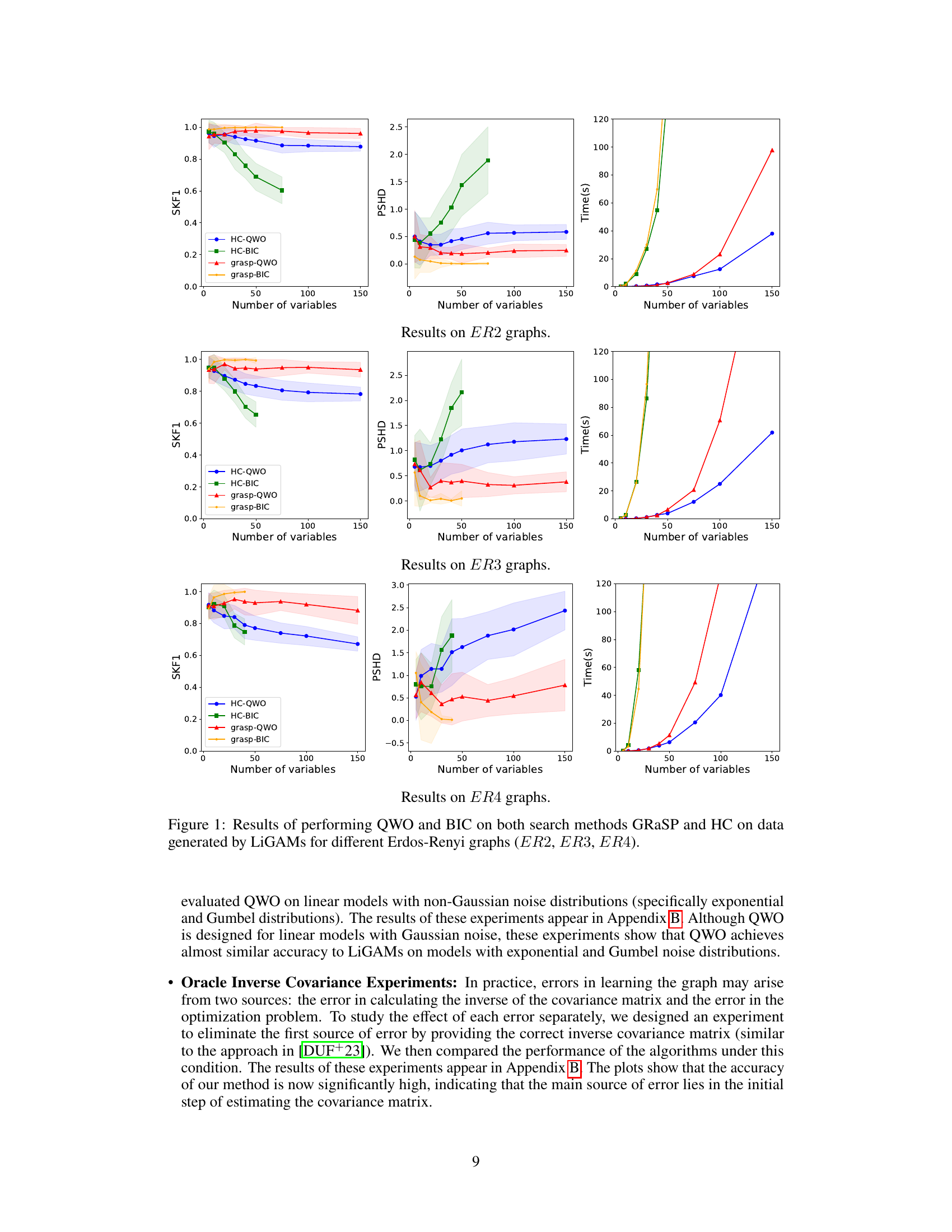
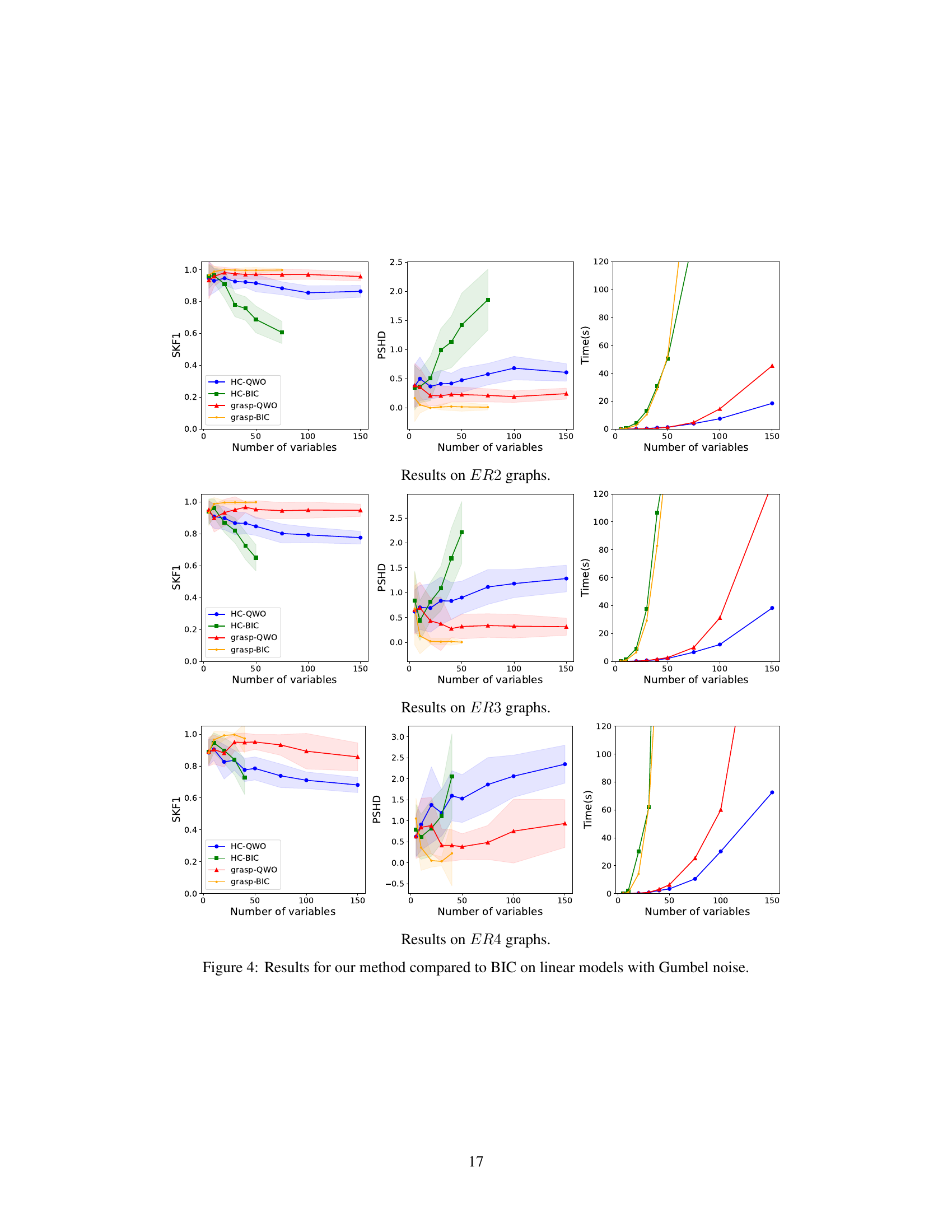
The figure presents the results of comparing QWO and BIC using GRaSP and Hill Climbing search methods on data generated by LiGAMs. Three different Erdos-Renyi graph types (ER2, ER3, ER4) were used, varying the number of variables. The plots show the SKF1 score (skeleton F1 score), PSHD (complete PDAG structural Hamming distance), and execution time for each method. The results illustrate that QWO consistently achieves higher accuracy with significantly reduced computational time compared to BIC, demonstrating its effectiveness across different graph structures and search strategies.
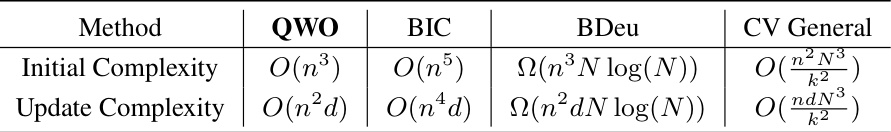
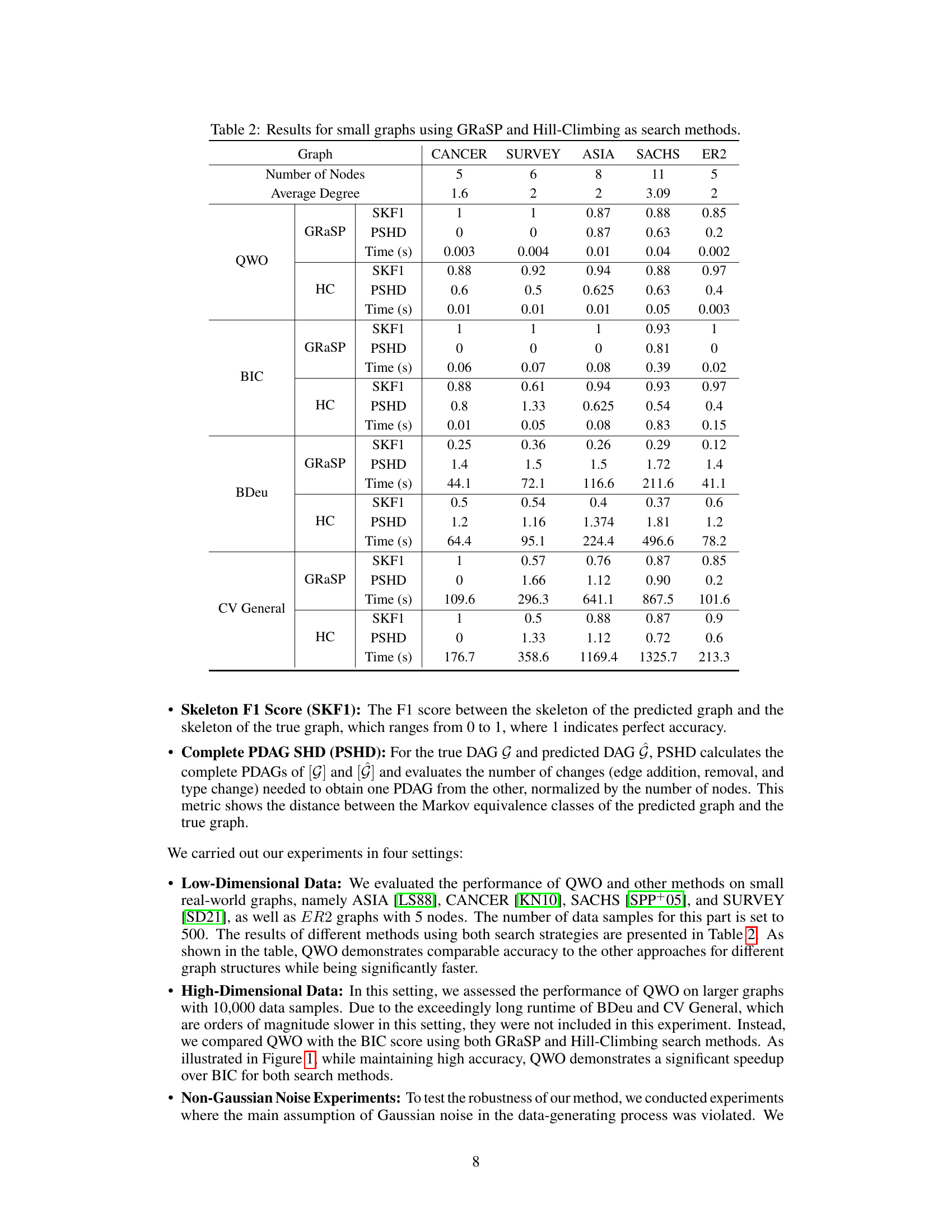
The table compares the time complexity of different methods for computing and updating the graph G’ in Linear Gaussian Acyclic Models (LiGAMs). It shows the initial complexity (for constructing the graph from scratch) and the update complexity (for updating the graph after a change in the permutation). The complexities are expressed in terms of n (the number of variables) and d (the length of the updated block of the permutation), and k for the CV General method (k-fold cross validation). The methods compared are QWO (the proposed method), BIC, BDeu, and CV General.
In-depth insights#
QWO: Causal Speedup#
The proposed QWO method significantly accelerates causal discovery in linear Gaussian acyclic models (LiGAMs) by improving the efficiency of computing the optimal directed acyclic graph (DAG) for a given permutation of variables. QWO achieves a speedup of O(n²) compared to state-of-the-art methods, making it particularly beneficial for large-scale causal inference problems. The method’s theoretical soundness is established, showing that it accurately constructs the optimal DAG under the specified assumptions. Furthermore, QWO seamlessly integrates with existing search strategies to enhance their performance. The scalability improvement offered by QWO is a substantial contribution, addressing the main bottleneck in permutation-based causal discovery. Its effectiveness is demonstrated empirically, showcasing a clear advantage in both speed and accuracy across different datasets and search algorithms. However, the limitations of LiGAM assumptions should be carefully considered; the approach may not be as effective for non-linear relationships, non-Gaussian noise, or cyclic causal structures. Further research could extend QWO to handle more complex causal settings while retaining its speed advantage.
LiGAM Causal Search#
LiGAM (Linear Gaussian Acyclic Model) causal search is a crucial problem in causal discovery, focusing on inferring causal relationships from observational data. The core challenge lies in efficiently searching the vast space of possible DAGs (Directed Acyclic Graphs) representing causal structures. Permutation-based methods offer a more efficient approach by exploring the space of causal orderings, significantly reducing the search complexity. However, even with this constraint, constructing the optimal DAG for a given permutation remains computationally expensive. This is where the innovation of algorithms like QWO (discussed in the provided text) becomes crucial, offering significant speedups in DAG construction while maintaining theoretical soundness. The efficiency gains achieved by algorithms such as QWO are vital for scaling causal discovery methods to higher-dimensional datasets with many variables, enabling the analysis of more complex systems. The combination of efficient search strategies and fast DAG construction methods is essential to advancing the field. Future research should explore extending these efficient methods beyond LiGAMs’ limitations, to broaden causal inference capabilities to diverse data types and more complex causal relationships.
QWO: Algorithmic Core#
The core of the QWO algorithm centers on efficiently computing and updating the graph Gπ for a given permutation π. This is achieved through a novel approach leveraging whitening transformations and orthogonal matrix manipulations. Instead of directly searching over possible DAGs, which is computationally expensive, QWO exploits the relationship between the covariance matrix of the variables, their causal ordering (encoded in π), and the resulting graph structure. The algorithm’s efficiency stems from its ability to incrementally update Gπ when the permutation π is modified, avoiding complete recomputation. Theoretical soundness is established, proving that QWO accurately constructs Gπ under certain assumptions (like Linear Gaussian Acyclic Models), and scalability is enhanced through a time complexity of O(n²d) for updates, where n is the number of variables and d is the length of the updated permutation block. This significant improvement over existing methods enables QWO to integrate seamlessly into search strategies like GRaSP and hill-climbing, significantly accelerating the overall causal discovery process.
Empirical Evaluations#
A robust empirical evaluation section is crucial for validating the claims made in a research paper. It should begin by clearly defining the metrics used to assess performance, justifying their selection based on their relevance to the research question. The experimental setup should be meticulously described, including details about datasets, data preprocessing steps, and the choice of baseline methods for comparison. Results should be presented clearly and comprehensively, ideally with visualizations such as graphs or tables that enhance understanding and facilitate comparison between different methods. Error bars or confidence intervals should be provided to convey the uncertainty inherent in empirical results. Importantly, the evaluation should not just focus on demonstrating superior performance in isolation. Rather, it should systematically explore the strengths and limitations of the proposed method under various conditions. This could involve varying hyperparameters, using different datasets, and conducting sensitivity analyses. A discussion of the results is key, providing insights into why a particular method might have performed well or poorly under specific conditions. Addressing potential limitations, such as confounding factors or biases, is also vital. Finally, the discussion section should connect the empirical findings back to the theoretical claims made in the paper, providing a cohesive narrative that strengthens the overall argument.
Future Research#
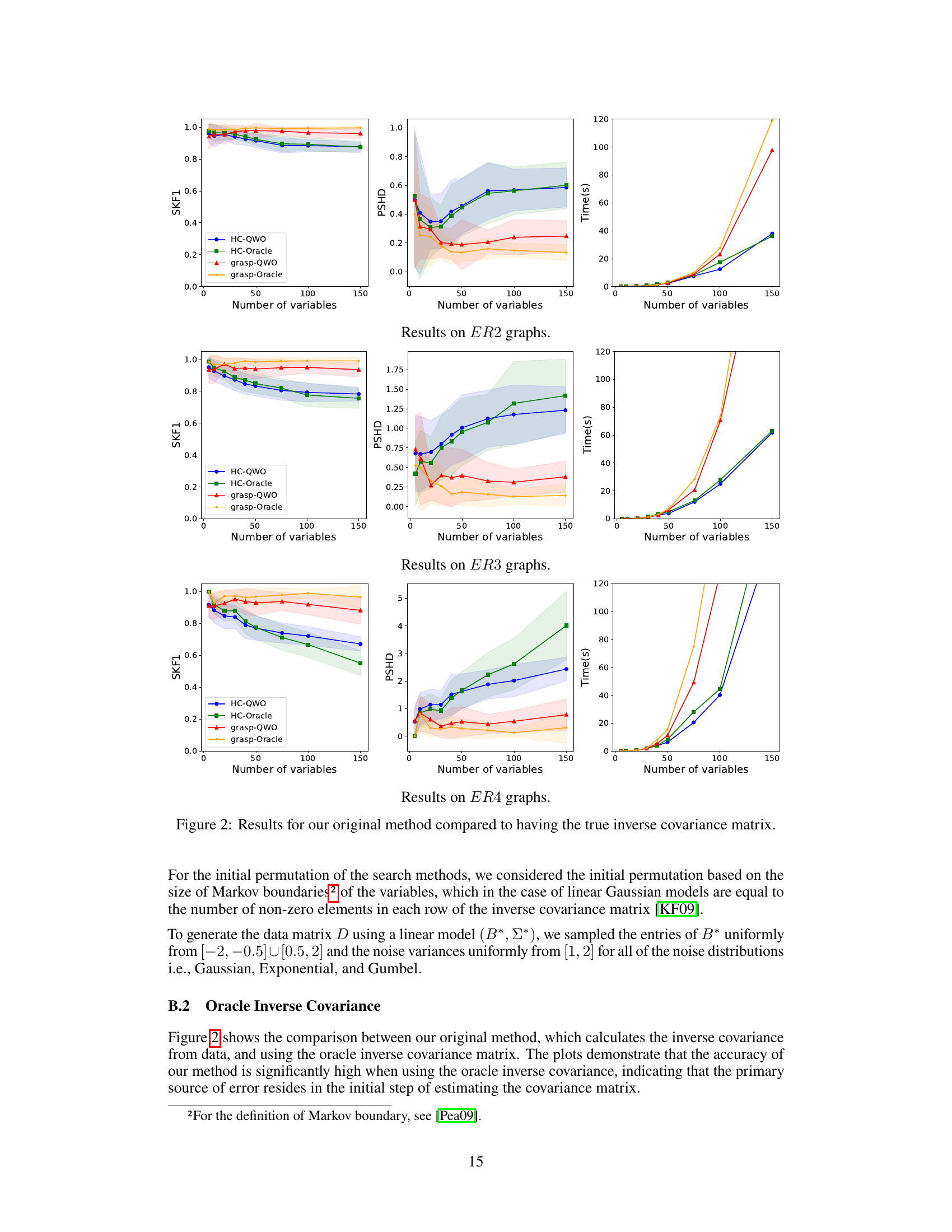
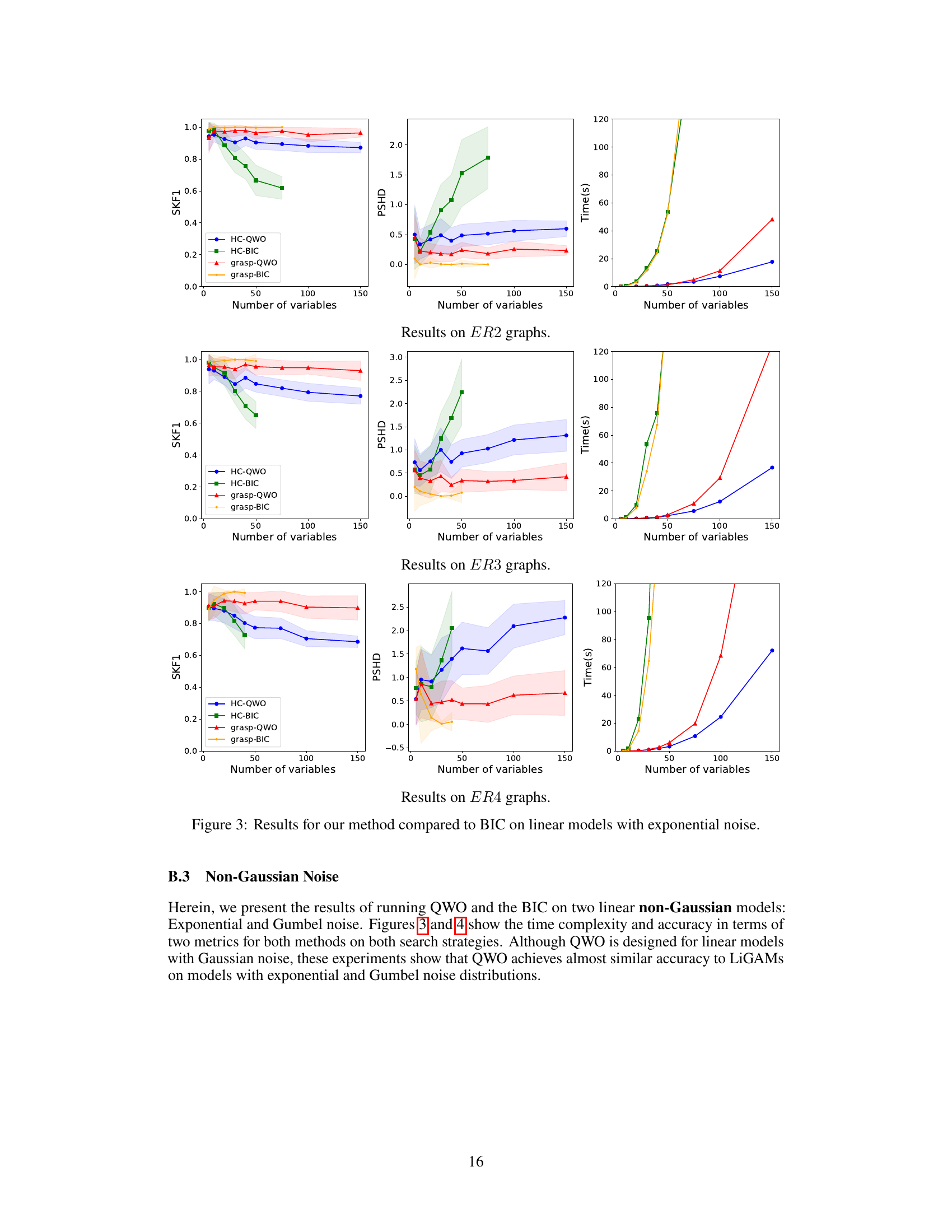
The paper’s conclusion highlights several promising avenues for future research. Extending QWO to handle non-linear relationships and non-Gaussian noise is crucial for broader applicability. Current limitations stem from the LiGAM assumption, so developing methods robust to violations of linearity and Gaussianity would greatly expand the algorithm’s usefulness. Addressing the challenges of cyclic causal graphs is another key area; the current framework is limited to acyclic models, making the extension to cyclic scenarios a significant advancement. Furthermore, improving the scalability of the search strategies, particularly for high-dimensional data, is a critical need. Exploring alternative score functions beyond BIC and investigating the effect of different search methods on QWO’s performance are worth investigating. Finally, thorough empirical evaluation on diverse datasets with varying characteristics would further validate QWO’s effectiveness and identify potential weaknesses.
More visual insights#
More on figures
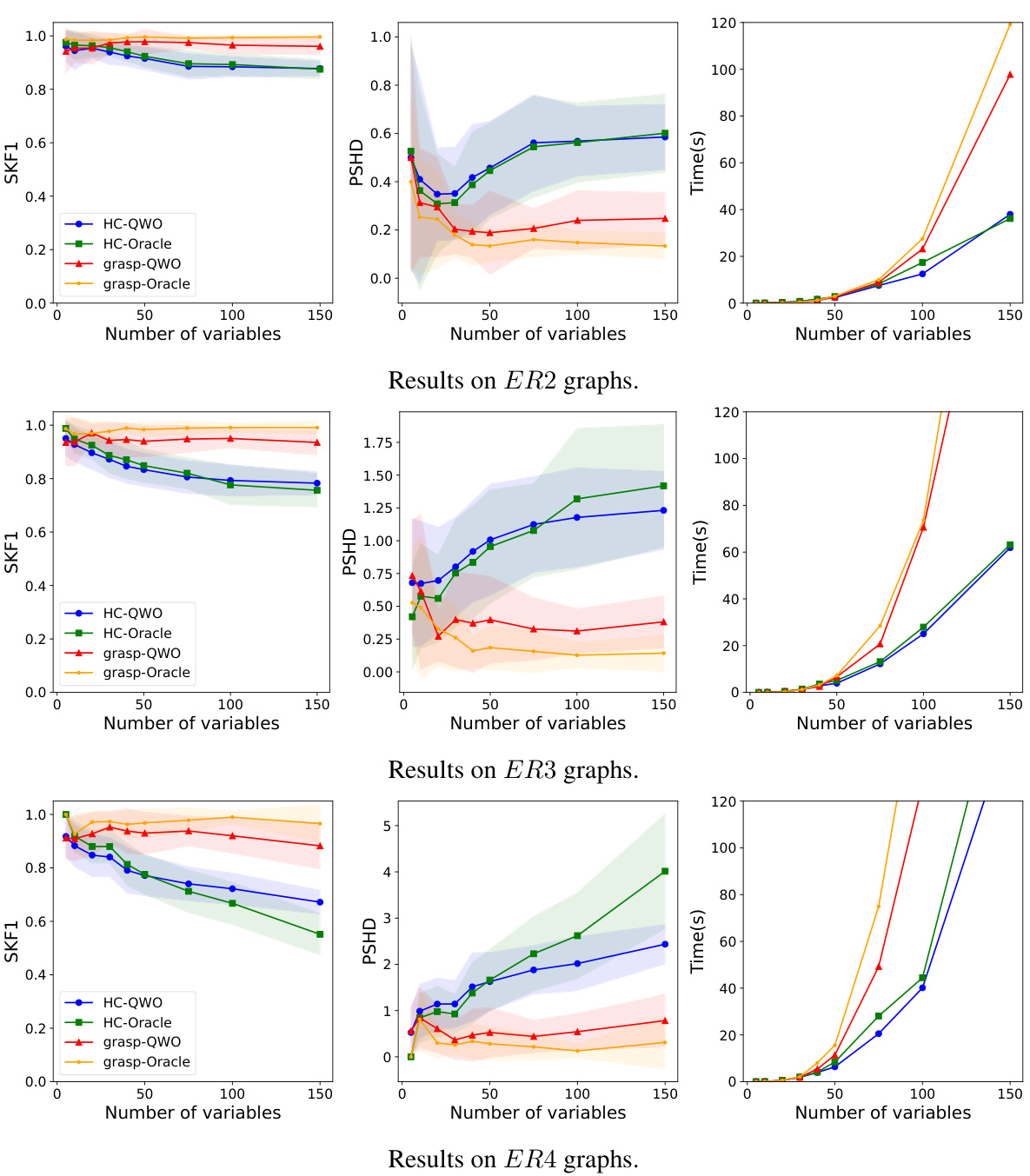
The figure displays the performance comparison of QWO and BIC using two different search methods, GRaSP and Hill Climbing, across various Erdos-Renyi graphs (ER2, ER3, ER4) in terms of SKF1 (Skeleton F1 Score), PSHD (Complete PDAG SHD), and execution time. The graphs show how the metrics vary with the number of variables and the impact of the graph structure on the algorithms’ performance. The shaded regions represent the standard deviation across multiple runs.

This figure compares the performance of QWO and BIC (Bayesian Information Criterion) using two different search methods (GRaSP and Hill Climbing) on Erdos-Renyi graphs with varying numbers of variables. It shows that QWO is significantly faster than BIC while maintaining comparable accuracy across multiple graph structures and search strategies. The plots display the SKF1 (Skeleton F1 Score), PSHD (Complete PDAG SHD), and runtime for each method.
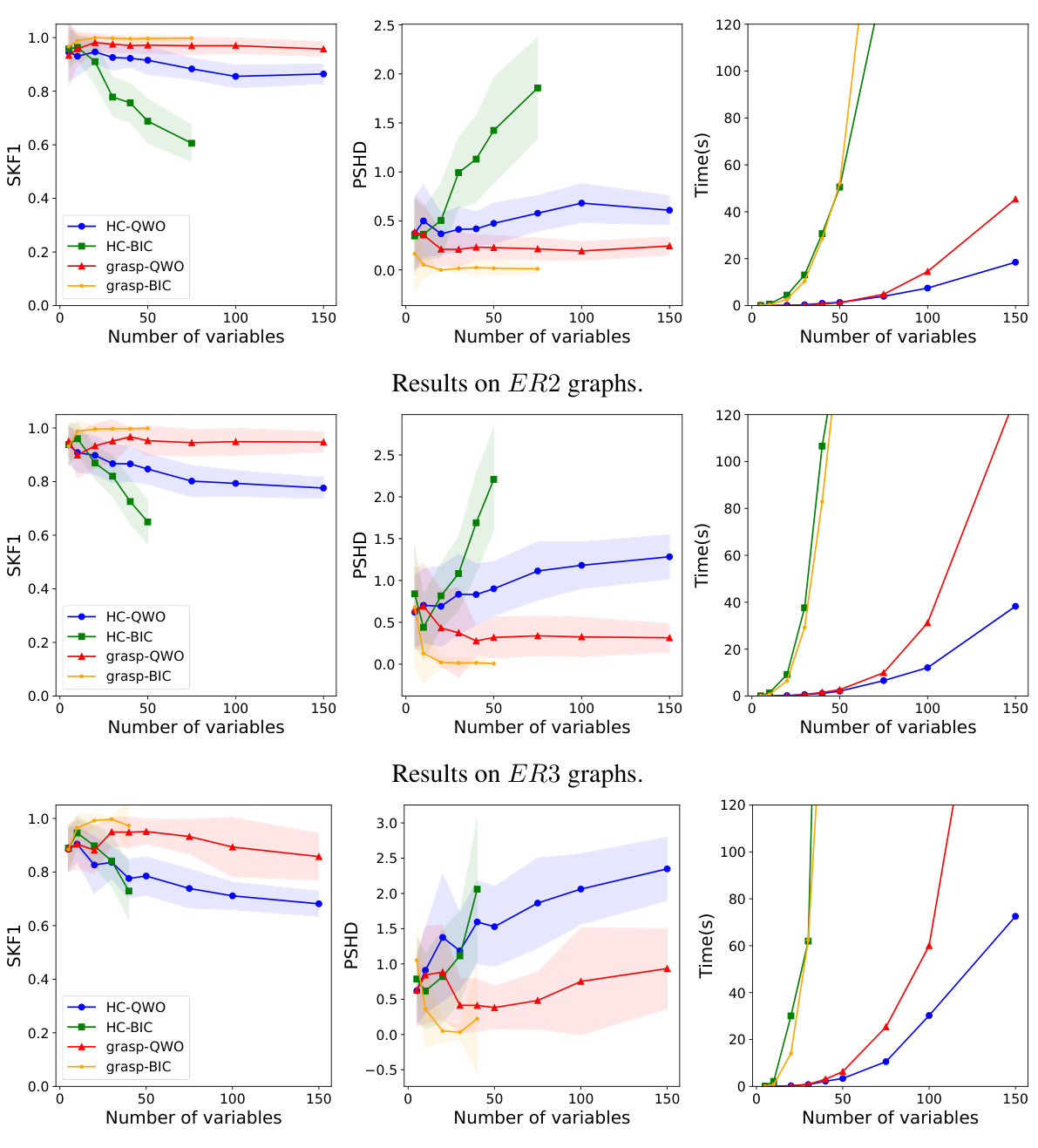
This figure shows the performance comparison between QWO and BIC using two different search methods, GRaSP and Hill Climbing, on three different types of Erdos-Renyi graphs (ER2, ER3, ER4). The comparison is based on three metrics: SKF1 (Skeleton F1 score), PSHD (Complete PDAG SHD), and Time (in seconds). The plots illustrate how the performance of each method varies with the number of variables in the graph. Each point in the plots represents the average of 30 experiments, with error bars representing the standard deviation. The results demonstrate that QWO achieves comparable accuracy to BIC while being significantly faster, especially as the number of variables increases. Different colors represent the different search strategies (HC-QWO, HC-BIC, grasp-QWO, grasp-BIC).
Full paper#