Hybrid Reinforcement Learning Breaks Sample Size Barriers In Linear MDPs

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it presents novel hybrid reinforcement learning algorithms that achieve significantly better sample efficiency than existing offline and online methods in linear Markov Decision Processes (MDPs). This is highly relevant to current trends focusing on improving RL sample efficiency and opens new avenues for research in hybrid RL techniques with linear function approximation, particularly regarding tighter theoretical bounds and improved algorithmic performance.

Visual Insights

#

This figure displays the results of an experiment evaluating the reward-agnostic exploration algorithm OPTCOV under different conditions. The x-axis shows the number of online episodes, and the y-axis displays the concentrability coefficient (a measure of how well the state-action space is covered). Three scenarios are compared: hybrid RL with a uniform behavior policy, hybrid RL with an adversarial behavior policy, and online-only exploration. The figure is split into three subplots representing the coverage of the entire state-action space, the offline partition, and the online partition. The results show that hybrid RL achieves better coverage than online-only exploration, even when the offline data is adversarially collected.

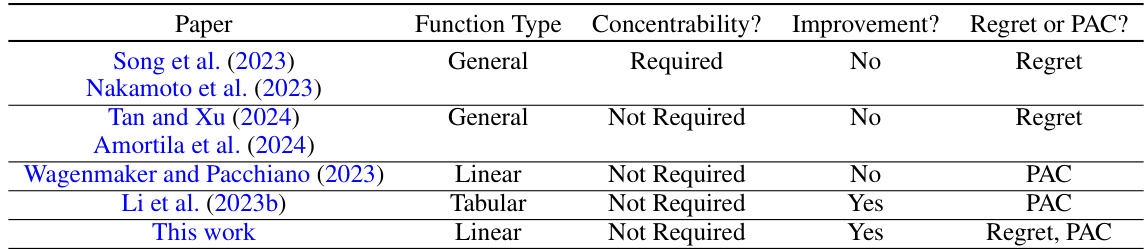
This table compares the paper’s contributions to existing hybrid reinforcement learning research. It contrasts different papers based on the function type used (general vs. linear vs. tabular), whether they require concentrability assumptions, if they show improvement over existing lower bounds for offline/online RL, and whether they focus on minimizing regret or obtaining a Probably Approximately Correct (PAC) guarantee.

In-depth insights

#

Hybrid RL’s Promise

#

Hybrid reinforcement learning (RL) holds significant promise by synergizing the strengths of offline and online RL. Offline RL leverages pre-collected data for efficient initial learning, reducing the need for extensive online exploration. Online RL, however, allows for adaptation and refinement of the learned policy in real-world, dynamic environments. This hybrid approach aims to overcome the limitations of each paradigm. Offline data can address the sample inefficiency often associated with online RL, while online exploration can mitigate the data bias and distribution shift issues inherent in offline RL. By intelligently combining these methods, hybrid RL strives to create more sample-efficient and robust algorithms, capable of achieving high performance in complex real-world scenarios where large datasets may be available but online interactions are essential for optimal decision making. The potential of hybrid RL is particularly significant for safety-critical applications where extensive online trial-and-error is impractical or unethical.

Linear MDP Analysis

#

A linear Markov Decision Process (MDP) analysis within a reinforcement learning context would likely focus on the representation of the dynamics and reward functions using linear models. This simplification allows for the application of linear algebra techniques to solve the Bellman equations and derive efficient algorithms. The analysis would likely explore sample complexity bounds under different assumptions on the behavior policy, including concentrability and coverage. Theoretical guarantees on the performance of algorithms, such as error bounds or regret bounds, could be derived. The analysis would also involve careful consideration of the curse of dimensionality, examining how the dimension of the feature space impacts the computational and sample efficiency of linear MDP algorithms. Comparison to non-linear function approximation would provide insights into the trade-offs between model accuracy and algorithmic complexity. Finally, the analysis might investigate the sensitivity of the algorithms to various hyperparameters and model misspecification.

Algorithmic Advance

#

An algorithmic advance in this research paper likely focuses on developing novel or improved reinforcement learning algorithms. This could involve enhancements to existing methods, such as improving sample efficiency or robustness to noisy data, or the creation of entirely new approaches, perhaps incorporating elements from other machine learning paradigms. The methods used might leverage recent developments in function approximation techniques or advanced exploration strategies. The core contribution might involve theoretical guarantees, demonstrating the algorithm’s performance under certain assumptions, such as bounds on regret or error or achieving minimax optimality. A key focus could be on addressing the limitations of pure offline or online RL by creating a hybrid approach which combines the strengths of both. This would show an improvement over the current state-of-the-art in the chosen RL setting (such as linear Markov Decision Processes or tabular cases), and likely involve rigorous mathematical analysis to support claims of performance enhancement. There could also be practical considerations addressed, such as computational efficiency and potential applications in real-world settings.

Empirical Validation

#

An Empirical Validation section would assess the claims made in a reinforcement learning research paper. It would likely involve experiments on benchmark environments (like linear Markov Decision Processes (MDPs) or more complex scenarios) using the proposed hybrid RL algorithms. Key aspects would be comparing performance against existing offline-only, online-only, and other hybrid methods. Metrics such as sample efficiency (for PAC bounds) and regret (for regret-minimization settings) are crucial. The design of experiments needs careful consideration, including the choice of behavior policies and the number of trials to ensure statistically significant results. The results section should clearly present quantitative comparisons, likely via tables and graphs. A discussion of the findings is also needed, exploring whether the empirical results align with the theoretical claims and also discussing any limitations or unexpected outcomes. The quality of behavior policies could be specifically investigated because the performance of the hybrid algorithms potentially depends on its quality. The discussion should delve into any implications for practical applications, and finally acknowledge any limitations of the experimental setup, potentially hinting at future research directions.

Future Directions

#

Future research could explore extending the hybrid RL framework to other function approximation methods beyond linear models, investigating the impact of different exploration strategies on sample efficiency and exploring hybrid RL in more complex environments such as those with continuous state spaces or partial observability. Addressing the theoretical challenges posed by high-dimensional state spaces and long horizons would be particularly valuable. It’s important to further investigate the interplay between offline and online data, potentially developing adaptive algorithms that automatically adjust the balance between the two based on the characteristics of the data and the learning process. Finally, a key area for future work would be to empirically evaluate the performance of hybrid RL on real-world tasks across diverse domains, comparing its efficiency and robustness to offline-only and online-only approaches. This would solidify the practical relevance of hybrid RL and highlight its potential benefits in situations where combining offline and online data offers unique advantages.

More visual insights

#

More on figures

This figure compares the performance of LinPEVI-ADV, a pessimistic offline RL algorithm, when trained on three different datasets: a hybrid dataset combining offline and online data, an offline-only dataset, and an online-only dataset. The online data was generated using an adversarial behavior policy, making the learning task more challenging. The y-axis represents the value of the learned policy (negative reward, higher is better), and the x-axis is not explicitly labeled in the image but likely represents an index of the trials. The box plot shows the distribution of policy values obtained across multiple runs of the algorithm, demonstrating that the hybrid approach leads to superior performance compared to offline or online learning alone under adversarial conditions.

This figure compares the performance of two algorithms: LSVI-UCB++ (an online-only reinforcement learning algorithm) and Algorithm 2 (the authors’ hybrid reinforcement learning algorithm). The top panel shows the cumulative regret over online timesteps, illustrating the total difference between the optimal reward and the reward achieved by each algorithm over time. The bottom panel displays the average per-episode reward over online timesteps, showing the average reward obtained per episode for each algorithm. Error bars representing one standard deviation are included to indicate variability in performance across the 10 trials. The results demonstrate that Algorithm 2, by leveraging offline data to initialize the online learning process, achieves lower regret and higher average reward compared to the online-only approach of LSVI-UCB++. This suggests the benefit of incorporating offline data into the online reinforcement learning process for improved performance.

Full paper

#