↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Neural network pruning aims to create smaller, faster models without sacrificing accuracy. Existing methods often focus on either efficiently scoring the importance of parameters (differentiable pruning) or on efficiently searching the space of sparse models (combinatorial optimization). This research reveals limitations in existing methods, as they develop independently along these two directions. Existing approaches have difficulties balancing performance gains from hardware utilization and computational efficiency.
The researchers propose SequentialAttention++, a novel algorithm that combines the strengths of both approaches. It uses differentiable pruning to guide combinatorial optimization, allowing for more accurate selection of important parameters to prune. Theoretically, they show that many existing differentiable pruning methods can be seen as nonconvex regularizations. Empirically, SequentialAttention++ achieves state-of-the-art results on ImageNet and Criteo datasets for block-wise pruning tasks, demonstrating its effectiveness and efficiency.
Key Takeaways#
Why does it matter?#
This paper is important because it bridges the gap between differentiable pruning and combinatorial optimization for neural network pruning, offering both theoretical and practical advancements. It provides a unified framework, novel algorithms, and improved empirical results, opening new avenues for research in efficient and scalable neural network training.
Visual Insights#
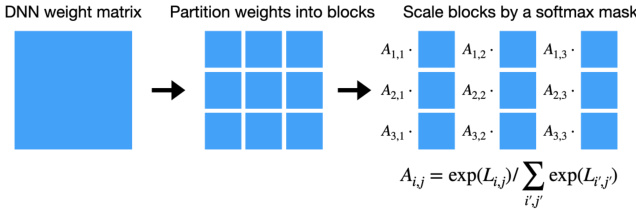
The figure illustrates the process of differentiable pruning applied to weight blocks. A dense weight matrix is first partitioned into smaller blocks. Then, each block is scaled by a softmax mask, Aij = exp(Lij) / Σi’j’ exp(Li’j’), where Lij represents the logits associated with the block. The softmax mask emphasizes the more important blocks by assigning them larger weights.

This table presents the results of block sparsification experiments using ResNet50 on the ImageNet dataset. It compares the validation accuracy of four different algorithms (ACDC, SequentialAttention++, Magnitude Pruning, and PowerPropagation) across various sparsity levels (70%, 80%, 90%, 95%) and block sizes (8x8, 16x16, 32x32, 64x64). Dashes indicate cases where the algorithms failed to converge due to extreme sparsity. For larger block sizes, the achieved sparsity is lower because only layers with at least 100 blocks are considered for pruning.
In-depth insights#
Block Sparse Pruning#
Block sparse pruning is a neural network optimization technique that enhances efficiency and performance by strategically removing less important connections. Unlike unstructured pruning which removes individual weights, block sparse pruning removes entire blocks of weights, leading to better hardware utilization and faster inference. This approach is particularly beneficial for large-scale models where unstructured pruning can be computationally expensive and might negatively impact model accuracy. Theoretical analysis of block sparse methods often involves non-convex regularization techniques to encourage sparsity and uniqueness of solutions. Algorithmic approaches commonly combine differentiable pruning methods to guide iterative selection of blocks to remove, improving pruning efficiency over one-shot methods. The optimal balance between sparsity and accuracy depends on factors like block size, the chosen regularization scheme, and the specific optimization algorithm used. Experimental results demonstrate improved efficiency and often comparable or even slightly better accuracy compared to unstructured counterparts. However, potential limitations include increased difficulty in ensuring the unique selection of blocks to prune and the potential of losing beneficial weight interactions. Further research is needed to explore novel regularization techniques and efficient algorithms for large-scale block sparse pruning to fully realize its potential.
Differentiable Scoring#
Differentiable scoring, in the context of neural network pruning, represents a significant advancement. It allows for the efficient and accurate assessment of the importance of individual network parameters or groups of parameters (e.g., blocks of weights). Unlike traditional methods relying on static metrics (such as magnitude pruning or Hessian-based scores), differentiable scoring integrates the importance evaluation directly into the training process. This is achieved by incorporating differentiable functions (e.g., soft masks or weight scaling) that dynamically modulate the parameter strengths. The gradients of these functions are then used to guide the pruning process, resulting in a more effective and accurate selection of parameters to retain, enabling better performance and efficiency. The differentiability of the scoring process makes it compatible with gradient-based optimization algorithms, seamlessly integrating the pruning procedure into the broader training pipeline. This approach allows for a data-driven assessment of parameter importance that evolves during training, leading to superior results compared to methods that rely on a static, fixed assessment of parameter importance.
SequentialAttention++#
The proposed method, SequentialAttention++, innovatively integrates differentiable pruning and combinatorial optimization for neural network block sparsification. Differentiable pruning efficiently scores the importance of parameters, while combinatorial optimization effectively searches the sparse model space. The algorithm cleverly uses a softmax mask to guide the selection of important blocks, thereby advancing the state-of-the-art. This approach is theoretically grounded, demonstrating that many differentiable pruning techniques can be viewed as nonconvex regularization, which in turn leads to a unique sparse solution. Empirical results on ImageNet and Criteo datasets validate its effectiveness in large-scale neural network pruning, achieving superior performance to existing methods. The inclusion of a novel sparsification phase further enhances performance by gradually pruning the least important features, facilitating a smoother transition between dense and sparse phases.
Theoretical Guarantees#
The theoretical guarantees section of a research paper would ideally provide a rigorous mathematical foundation for the claims made. This often involves proving the correctness and efficiency of algorithms or models under specific conditions. For example, convergence proofs might demonstrate that an algorithm reliably reaches a solution, while bounds on the approximation error could quantify the accuracy of an approximate solution. It’s crucial to carefully define assumptions, such as the type of data, the model’s architecture, and the nature of the optimization landscape (e.g., convexity, smoothness). A strong theoretical foundation increases the reliability of the findings and enhances the paper’s overall impact by offering confidence beyond just empirical results. The absence or weakness of theoretical guarantees can significantly weaken the argument, particularly in cases where empirical results could be subject to various confounding factors. Therefore, a robust theoretical section is essential for establishing a comprehensive and trustworthy contribution to the field.
Future Directions#
The research paper’s “Future Directions” section could explore several promising avenues. Extending the theoretical framework to encompass a broader range of loss functions and network architectures would strengthen its generalizability. Investigating the impact of different block sparsity patterns on model performance and efficiency is crucial, going beyond square blocks. A detailed analysis of the algorithm’s scalability to extremely large-scale models and datasets is warranted. Additionally, a comparison with other state-of-the-art structured pruning methods using a more extensive set of benchmarks would further validate the proposed method’s effectiveness. Finally, exploring the implications of the unique sparse global minima property for model interpretability and robustness to adversarial attacks could uncover valuable insights, while examining the method’s applicability to other domains beyond image classification and recommendation systems is essential.
More visual insights#
More on figures

Figure 2(a) compares the effectiveness of using softmax attention scores versus magnitude (Frobenius norm) for block importance scores in pruning. It shows the difference in validation accuracy (in percentage points) between models pruned using softmax attention and those pruned using magnitude, for various block sizes and sparsities. A positive value indicates that softmax attention outperforms magnitude pruning. Figure 2(b) illustrates the sparsity schedules used in ACDC and SequentialAttention++. ACDC uses a sharp transition between dense and sparse phases, while SequentialAttention++ employs a smoother, exponential sparsity schedule during the SPARSIFICATION phase.

The figure illustrates the process of differentiable pruning applied to weight blocks in a neural network. The weight matrix is partitioned into blocks, each block is scaled by a softmax mask (calculated from logits L), and the process is guided by differentiable pruning techniques. This figure is crucial for understanding the proposed SequentialAttention++ algorithm, which extends differentiable pruning to improve block sparsification.

This figure illustrates the process of differentiable pruning applied to blocks of weights in a neural network. The weight matrix is partitioned into blocks. Each block is then scaled by a softmax mask, where the mask values are determined by the exponentiation of logits and normalization, resulting in a sparse representation. This process integrates differentiable pruning techniques with combinatorial optimization to achieve efficient and accurate pruning.
More on tables
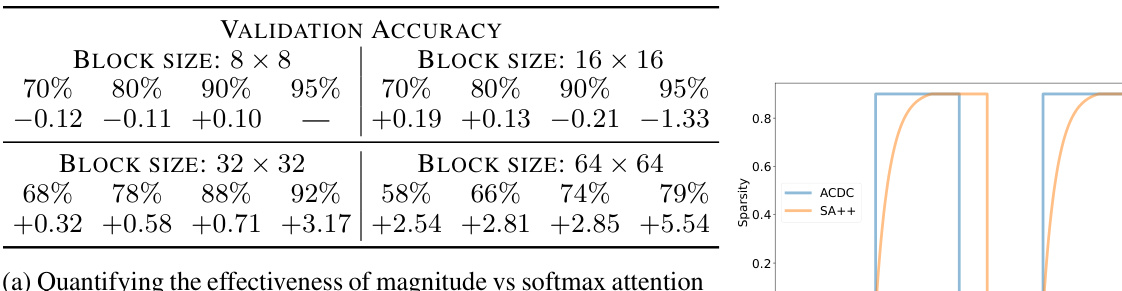
This table presents the results of block sparsification experiments using ResNet50 on the ImageNet dataset. It compares the validation accuracy of four different pruning algorithms (Magnitude, PowerPropagation, ACDC, and SequentialAttention++) across various block sizes (8x8, 16x16, 32x32, 64x64) and sparsity levels (70%, 80%, 90%, 95%). The baseline validation accuracy (no pruning) is 76.90%. Dashes indicate cases where algorithms failed to converge due to excessive sparsity. For larger block sizes, the actual sparsity achieved is lower because only layers with at least 100 blocks are pruned.

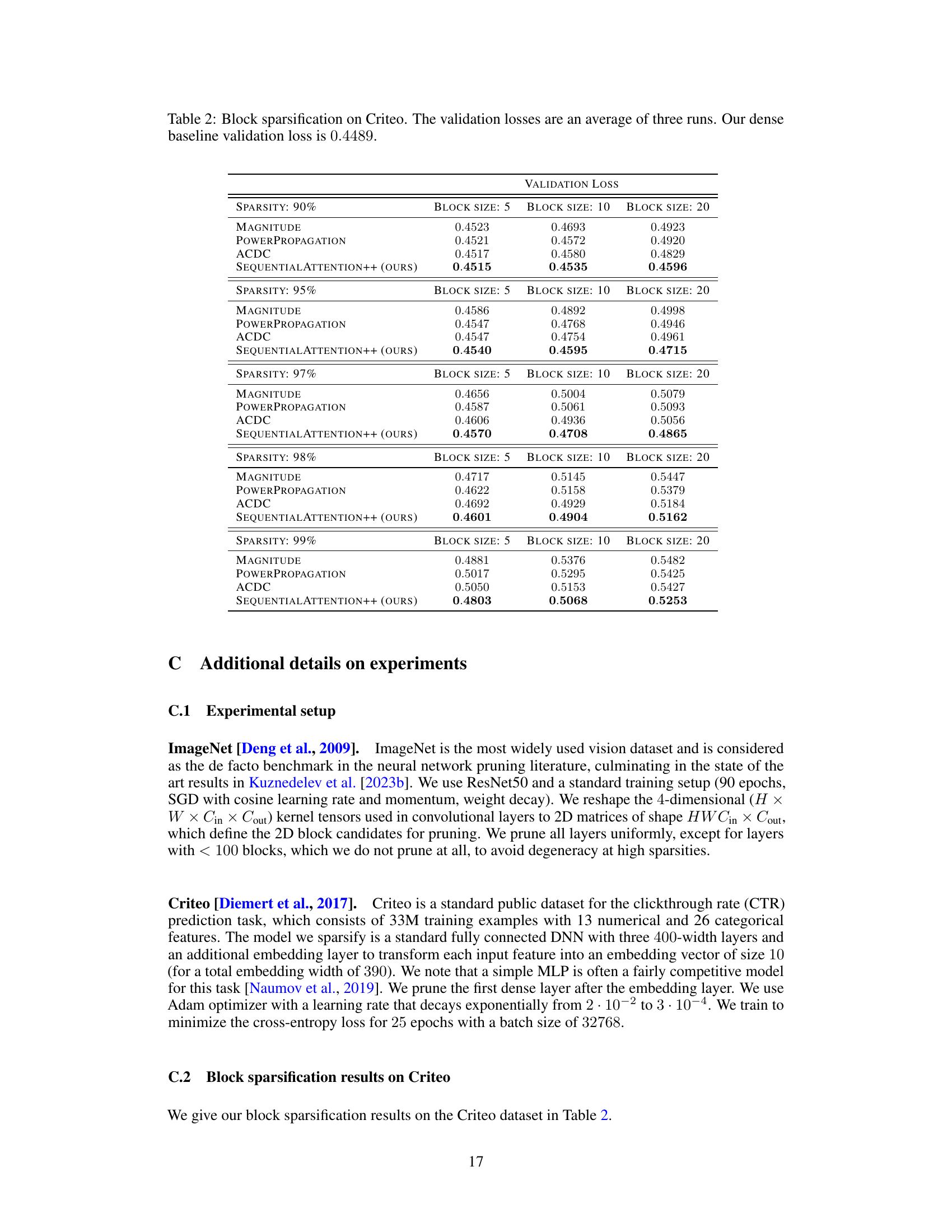
This table presents the results of block sparsification experiments on the Criteo dataset. It compares four different algorithms (Magnitude, PowerPropagation, ACDC, and SequentialAttention++) across varying sparsity levels (90%, 95%, 97%, 98%, 99%) and block sizes (5, 10, 20). The validation loss, averaged over three runs, is reported for each combination of algorithm, sparsity, and block size. A baseline validation loss for a dense model (0.4489) is also provided for comparison.

This table presents the results of block sparsification experiments on the ResNet50 model trained on the ImageNet dataset. It compares the validation accuracy achieved by four different algorithms: ACDC, SequentialAttention++, Magnitude Pruning, and PowerPropagation, across various sparsity levels (70%, 80%, 90%, 95%) and block sizes (8x8, 16x16, 32x32, 64x64). Dashes indicate cases where algorithms failed to converge due to excessive sparsity. For larger block sizes, the actual sparsity is lower because only layers with at least 100 blocks were pruned.

This table presents the results of an ablation study on the impact of modifying the exponent constant (c) used in the sparsity schedule of the SPARSIFICATION phase within the SequentialAttention++ algorithm. ResNet50 was trained on ImageNet with a target sparsity of 90%, and different block sizes (8x8, 16x16, 32x32, 64x64) were evaluated. The table shows the validation accuracy achieved for different values of c (2, 4, and 8). This allows assessing the impact of the rate at which the sparsity increases during the SPARSIFICATION phase on the final model’s performance.
Full paper#