↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Large Language Models (LLMs) are increasingly used in iterative processes, creating feedback loops that can amplify biases present in initial models. This poses a significant challenge as it can lead to undesirable outcomes. The paper highlights the lack of systematic understanding of these processes and the need for effective methods to guide LLM evolution in desired directions.
This paper proposes leveraging Iterated Learning (IL), a Bayesian framework, to analyze this iterative process. It theoretically justifies approximating LLM in-context behavior with a Bayesian update, then validates this through experiments with various LLMs. The study’s key contribution is a novel framework to predict and guide LLM evolution, offering strategies for bias mitigation or amplification based on the desired outcome.
Key Takeaways#
Why does it matter?#
This paper is crucial because it provides a novel framework for understanding and guiding the evolution of LLMs by drawing parallels between their behavior and human cultural evolution. This is essential given the increasing prevalence of iterative interactions among LLMs and their potential for both beneficial and harmful bias amplification. The framework’s predictive power, supported by experimental verification, offers researchers valuable insights into LLM development and alignment, paving the way for safer and more beneficial AI systems.
Visual Insights#
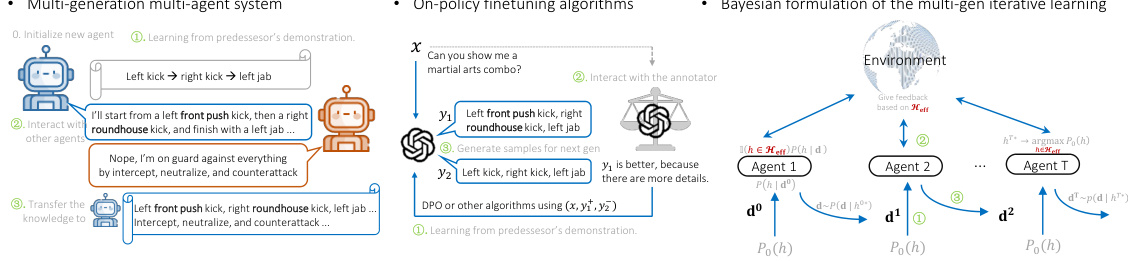
This figure illustrates how practical LLM systems, such as multi-generation multi-agent systems and on-policy finetuning algorithms, involve knowledge transfer between different generations. It maps these practical systems onto a Bayesian agent model, highlighting the three key phases: imitation (learning from a predecessor’s demonstration), interaction (refining knowledge through interaction with an annotator or environment), and transmission (generating samples for the next generation). The figure visually represents how biases might be amplified or mitigated during this iterative process by comparing the results of interactions with an annotator.

This table presents the results of experiments comparing different methods for guiding the evolution of LLMs. Three different LLMs (Old GPT3.5-Turbo, New GPT3.5-Turbo, and Claude3-haiku) were used, each with three different interaction phase methods: imitation-only, self-refine, and hypothesis-search. The table shows the correlation between the model’s predictions and the ground truth (Corr. d), the percentage of times the model predicted that the screen was off (r20=off), and the percentage of times both the correlation and screen: off condition were met (BOTH). The results demonstrate how different interaction phases affect the LLM’s ability to learn correctly and reduce bias.
In-depth insights#
Bias Amplification#
The concept of ‘Bias Amplification’ in the context of language model evolution is a critical one. The paper explores how iterative learning processes, where models learn from data generated by previous models, can lead to an exponential magnification of subtle biases present in initial models or training data. This occurs because each successive model inherits and potentially exacerbates the biases of its predecessors, creating a feedback loop that reinforces and amplifies these biases over time. The authors highlight that this amplification can be both beneficial (e.g. strengthening desirable properties) and harmful (e.g., amplifying undesirable biases or limiting creativity). Understanding and managing this amplification process is crucial for developing effective strategies for guiding the evolution of LLMs in desired directions, such as through careful design of the training data or using mechanisms to filter or rerank data to mitigate bias during the iterative learning process. The Bayesian iterated learning (IL) framework provides a valuable tool for analyzing and predicting the effects of bias amplification, offering a theoretical basis for understanding these complex dynamics and informing the design of effective bias mitigation and alignment techniques for the future evolution of LLMs.
Iterated Learning#
Iterated learning, a concept central to the provided research, models the iterative process of knowledge transmission and refinement across multiple generations of learners. The paper highlights its relevance to large language models (LLMs), suggesting that the sequential training and refinement of LLMs bear a striking resemblance to iterated learning in human cultures. The core idea is that subtle biases present in initial data or models can become amplified across generations, leading to the evolution of cultural traits (or in the case of LLMs, model behaviors). This bias amplification is a double-edged sword: while beneficial biases might be reinforced, harmful ones could be magnified, thus raising concerns about unintended consequences. The study proposes a Bayesian framework for analyzing this phenomenon, emphasizing the importance of carefully designing interaction phases to mitigate or guide the direction of bias amplification in LLMs. This framework provides a theoretical lens for understanding the long-term evolutionary trajectories of LLMs, and offers valuable insights for ensuring the responsible and beneficial development of this transformative technology.
LLM Evolution#
The concept of “LLM Evolution” is a fascinating one, particularly when considered through the lens of iterative learning. The iterative nature of LLM improvement, where models generate data used to train subsequent models, creates a feedback loop with significant implications. This process is not unlike biological evolution; subtle biases or preferences present in early models get amplified over time, possibly leading to unintended consequences. The paper highlights the importance of understanding this evolutionary process to better guide LLM development towards desired outcomes, such as reducing harmful biases or enhancing creativity. A key aspect of the research involves analyzing this evolution using Bayesian iterated learning, a framework for understanding how biases are magnified in cultural transmission. The research suggests that incorporating an explicit “interaction phase” to filter or refine the LLM-generated data could prove vital in steering this evolution toward more beneficial paths. This involves acknowledging that bias amplification is a double-edged sword, capable of both exacerbating problems and enhancing desirable traits. The findings call for a more nuanced approach to LLM development, moving beyond simple performance metrics and incorporating a deeper understanding of the long-term impacts of iterative training and the complex dynamics of model evolution.
Bayesian Analysis#
A Bayesian analysis in a research paper would likely involve applying Bayesian statistical methods to analyze data and draw inferences. This approach contrasts with frequentist methods by explicitly incorporating prior knowledge or beliefs about the parameters of interest into the analysis. Key aspects of a Bayesian analysis often include specifying a prior distribution, calculating the likelihood function based on the observed data, and computing the posterior distribution using Bayes’ theorem. The posterior distribution represents the updated belief about the parameters after considering both the prior knowledge and the observed data. The selection of appropriate prior distributions is critical, as it influences the final results. Different types of prior distributions can be used depending on the available information and assumptions. The analysis might involve using computational methods such as Markov Chain Monte Carlo (MCMC) or variational inference to approximate the posterior distribution when it’s difficult to calculate analytically. The results of a Bayesian analysis are typically presented as credible intervals or posterior distributions, which provide a range of plausible values for the parameters of interest along with their associated probabilities. The interpretation of results must be cautious and should acknowledge both the prior assumptions and the uncertainty inherent in Bayesian methods. Model comparison may also be part of the analysis if evaluating the performance of different models is relevant. Overall, a well-executed Bayesian analysis can offer a flexible and comprehensive approach to statistical inference, which goes beyond frequentist statistics by explicitly incorporating prior information and providing a complete probability distribution for the parameters.
Future of LLMs#
The future of LLMs is intrinsically linked to their ability to learn and evolve iteratively. Bias amplification, a significant concern, highlights the need for careful algorithm design and ongoing monitoring. The paper suggests that a Bayesian framework for iterated learning can help predict and guide LLM evolution, emphasizing the importance of a well-defined interaction phase to filter or refine LLM outputs. This framework offers a systematic approach to manage biases, potentially mitigating negative societal impacts and promoting beneficial outcomes. The long-term impact hinges on resolving challenges related to understanding and controlling the amplification of both beneficial and harmful biases. The design of effective interaction phases is key to steering LLMs toward desirable trajectories, preventing the uncontrolled magnification of biases, and ensuring alignment with human values. Further research focusing on the implicit nature of LLMs’ knowledge and the development of mechanisms for nuanced interaction will be crucial for realizing the full potential of LLMs while mitigating risks.
More visual insights#
More on figures
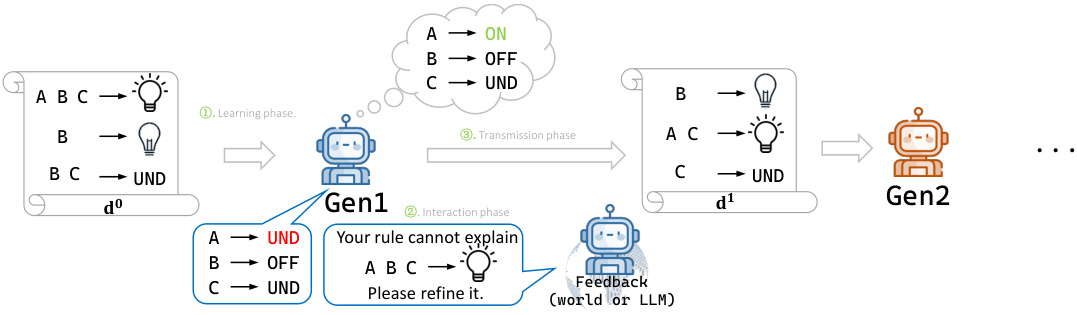
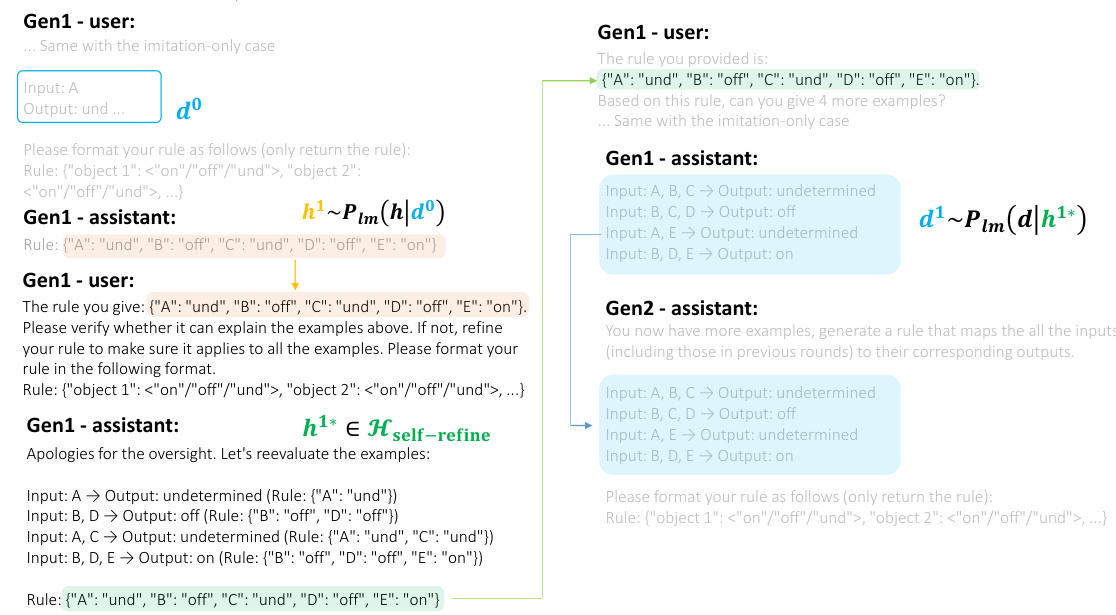
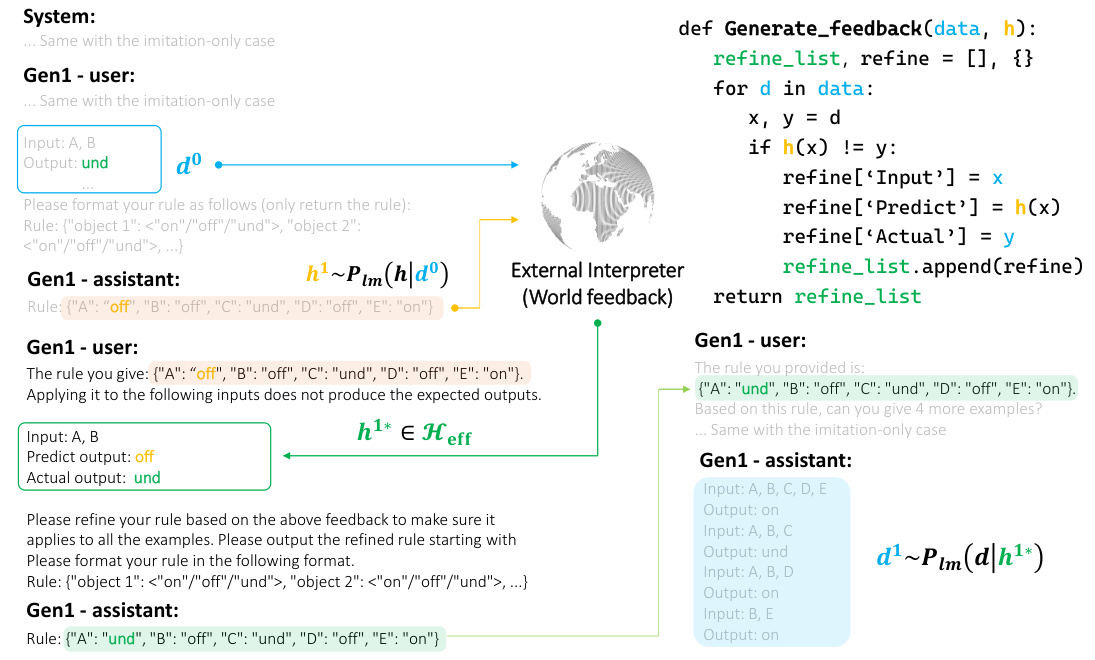
This figure demonstrates how iterated in-context learning is performed on the Abstract Causal Reasoning (ACRE) task. It shows how an LLM agent learns from examples, refines its knowledge through an interaction phase (involving feedback from a human or another LLM), and then generates new examples for the next generation. The figure shows the transfer of knowledge between generations and how an agent’s belief of a rule (h) is updated over time.

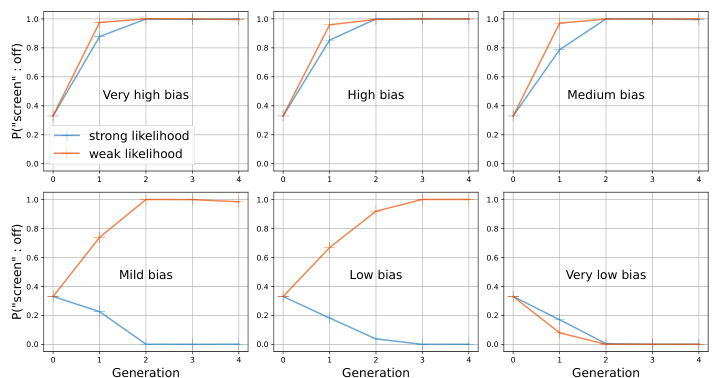
This figure shows the results of experiments designed to visualize how the posterior distribution of hypotheses (h), entropy (H(Plmw(h))), and the probability of a specific bias (‘screen: off’) evolve across multiple generations of iterated learning. The left panel shows the entropy of the posterior distribution decreasing over generations for various temperature settings, indicating convergence. The middle two panels illustrate the evolution of the probability of the ‘screen: off’ bias under different prior bias levels and likelihood conditions. The right panel displays histograms of the posterior distribution for the first and sixth generations, visually representing the amplification of the prior bias.

This figure shows the results of two sets of experiments. The left three panels show the results from the experiments in section 6, which studies how the ratio of easy samples, the average ranking of acronyms, and average length of acronyms change over generations in a self-data augmentation task. The right two panels shows the results from the experiments in section 7, which studies the effect of on-policy DPO on the average length of responses and win rate against SFT baseline. Different lines represent different initial conditions (number of easy examples in d⁰ and different bias settings).

This figure illustrates the analogy between the Expectation-Maximization (EM) algorithm and the imitation-only iterated learning. The EM algorithm is a general method for finding maximum likelihood estimations in statistical models with hidden variables, iteratively improving an estimation of the parameters by updating a distribution over the hidden variables (E-step) and then maximizing the likelihood given this distribution (M-step). The figure shows how the imitation-only iterated learning mirrors the EM algorithm. In the imitation-only iterated learning, agents learn from data samples generated by previous agents, updating their beliefs about the underlying hypothesis (analogous to the E-step in EM). The next generation of agents then samples new data based on these updated beliefs (analogous to the M-step in EM), and the process repeats, thus iteratively refining the hypothesis.

This figure illustrates how practical LLM systems, which involve knowledge transfer across multiple generations, can be approximated using Bayesian agents. The three phases of iterative learning (imitation, interaction, and transmission) are highlighted, showing how knowledge is acquired from predecessors, refined through interaction, and transmitted to the next generation. The figure uses diagrams to visualize the flow of information between agents and the Bayesian updating process that occurs during each phase.

This figure shows the prior probability distribution of all possible mappings (hypotheses, h) from the input set X to the output set Y in the iterated learning experiment. The x-axis represents the index of the 256 possible mappings, while the y-axis represents the prior probability Po(h) of each mapping. The mappings are categorized into four groups: degenerate, holistic, others, and systematic. The figure visually demonstrates that degenerate mappings have the highest prior probability, followed by holistic mappings, systematic mappings, and then ‘others’. This distribution reflects an inherent bias towards simpler or less complex mappings.

This figure shows the results of four different iterated learning experiments. Each experiment tracks the proportion of three different types of mappings (degenerate, holistic, and systematic) over multiple generations. The first two experiments demonstrate the amplification of bias with an interaction phase, starting from holistic and degenerate mappings. The third experiment shows that the lack of an interaction phase leads to the dominance of degenerate mappings. The final experiment shows how eliminating the compressibility pressure (using a uniform prior) affects the proportions of the different mapping types.
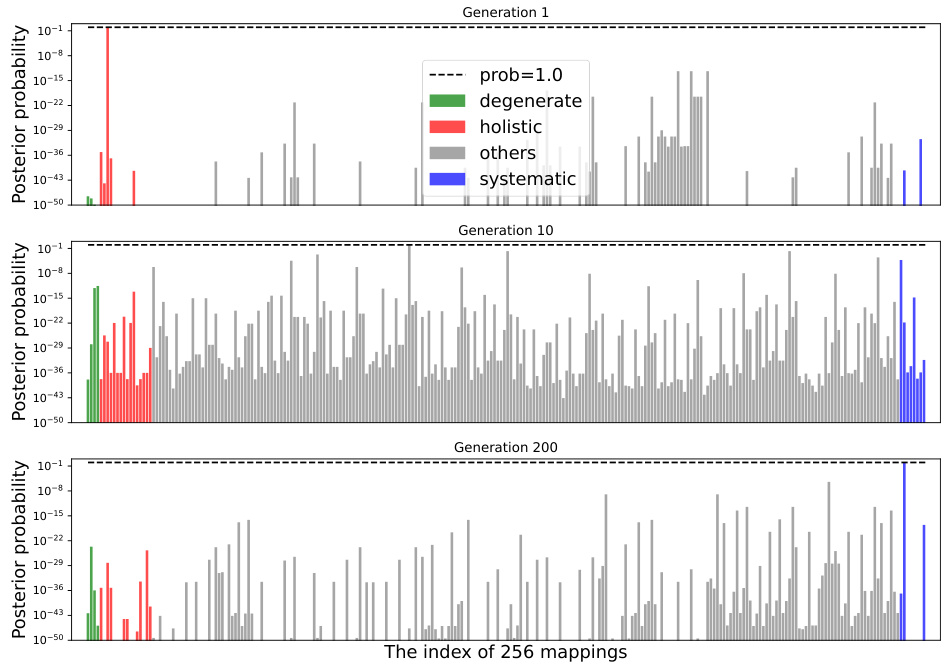
This figure shows the posterior probabilities of all 256 possible mappings (hypotheses) at different generations (1, 10, and 200) during the iterated learning process. The different colors represent different categories of mappings: degenerate, holistic, others, and systematic. It visually demonstrates the shift in probability mass towards systematic mappings as the iterative learning progresses, highlighting the effect of both compressibility and expressivity pressures.

This figure illustrates how practical LLM systems, which involve iterative knowledge transfer among different generations, can be approximated using Bayesian agents within an iterated learning (IL) framework. The figure showcases three key phases of the process: 1. Imitation Phase: A new agent learns from data generated by its predecessor. 2. Interaction Phase: The agent interacts with the environment, refining its knowledge. 3. Transmission Phase: The agent generates new data to be used by the subsequent generation of agents. The figure visually represents these steps using diagrams of multi-agent systems, highlighting how Bayesian agents approximate the behavior of LLMs in this iterative, knowledge-transfer process.
This figure illustrates how practical LLM systems, involving multi-agent and multi-generational interactions, can be modeled using Bayesian agents. It highlights the three key phases of iterative learning: imitation (agent learns from a predecessor), interaction (agent refines its knowledge through tasks), and transmission (agent shares knowledge with the next generation). The figure uses a multi-generation, multi-agent system to show how LLMs learn from other LLMs or themselves over time, and how this process can be seen as a Bayesian update of the agent’s prior knowledge.
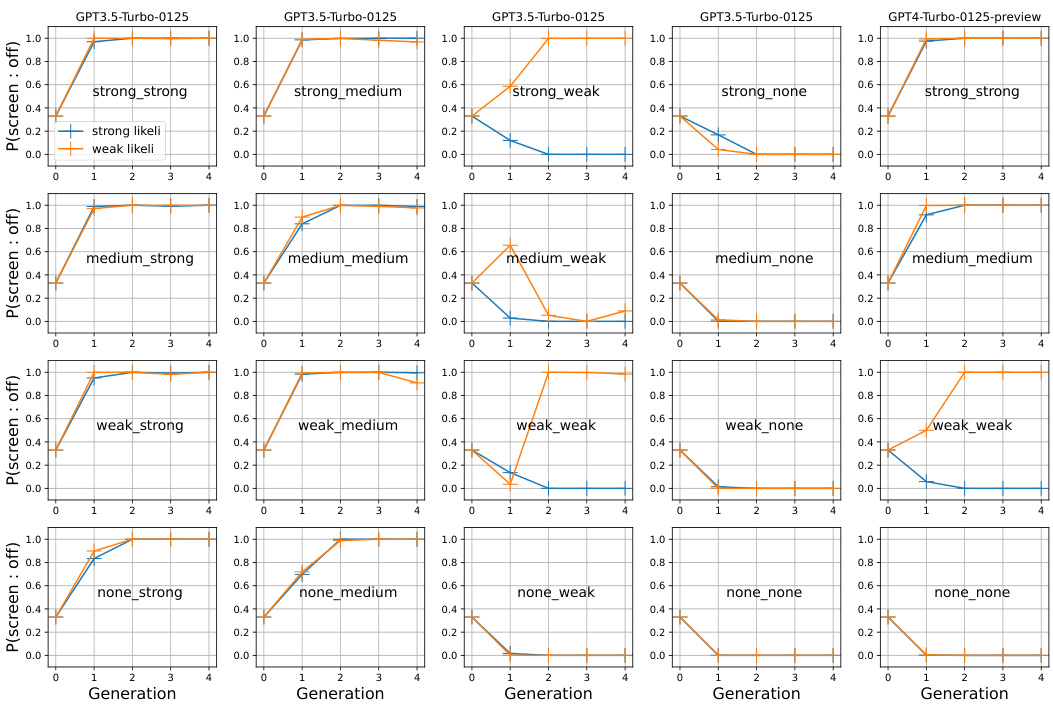
This figure presents a multi-faceted analysis of the evolution of the posterior distribution P(h) across multiple generations of iterated learning. The left panel shows the entropy of the posterior distribution (H(Plmw(h))) decreasing over time for both strong and weak likelihood scenarios, indicating convergence. The central panels illustrate the impact of varying degrees of prior bias on the probability of ‘screen:off’ over different generations. The right panels display histograms showing how the posterior distribution evolves from a relatively flat distribution in generation 1 to a much more peaked one in generation 6, illustrating the concentration of probability on a limited subset of hypotheses (h). Different colors represent different levels of spurious bias.
This figure presents an analysis of how bias is amplified in iterated learning using Large Language Models (LLMs) in an inductive reasoning task. The left panel shows the entropy of the posterior distribution of hypotheses (H(Plmw(h))), decreasing over generations, indicating convergence. The middle panels show the probability of ‘screen:off’, demonstrating how different prior biases and likelihoods affect the convergence speed. The right panels display histograms of the posterior distributions, illustrating bias amplification.

This figure illustrates how Bayesian agents can be used to model the behavior of LLMs in practical systems that involve knowledge transfer between generations. The three phases of iterated learning—imitation, interaction, and transmission—are highlighted, showing how an LLM learns from previous generations’ data (imitation), refines its understanding through interaction with the environment or other agents (interaction), and then generates new data for subsequent generations (transmission). The figure uses a multi-generation, multi-agent system to visually represent this iterative process, showing how biases and knowledge evolve over time.
This figure illustrates how practical LLM systems, which involve knowledge transfer between generations (e.g., iterative self-data-augmentation, multi-agent LLM systems), can be approximated using Bayesian agents in an iterated learning framework. The three phases highlighted are imitation, interaction, and transmission. The imitation phase shows how a new agent learns from the previous generation’s output. The interaction phase represents refinement of knowledge, perhaps through interaction with the environment, feedback from other agents, or other processes. Finally, the transmission phase illustrates the transfer of knowledge from one generation of agents to the next.
This figure illustrates the process of iterative learning among different generations of LLMs. It shows how LLMs can be approximated by Bayesian agents and how each generation of agents engages in three phases: imitation (learning from the previous generation), interaction (refining knowledge through tasks or feedback), and transmission (generating data for the next generation). The figure visually represents this iterative process using diagrams of multi-generation multi-agent systems, on-policy finetuning algorithms, and a Bayesian formulation of the multi-gen iterative learning process.

This figure shows the prompt design for an acronym brainstorming task using an LLM. The design involves iterated learning, with each generation producing new examples based on previous generations. The examples are generated by the LLM based on the provided prompts and constraints. The figure also highlights the process of imitation-only and interaction with different Heff (set of hypotheses that accomplish the task). The imitation-only setting involves the LLM generating new examples based solely on the initial set of examples, while the interaction with different Heff involves incorporating feedback from a carefully designed interaction phase to refine the generated examples.
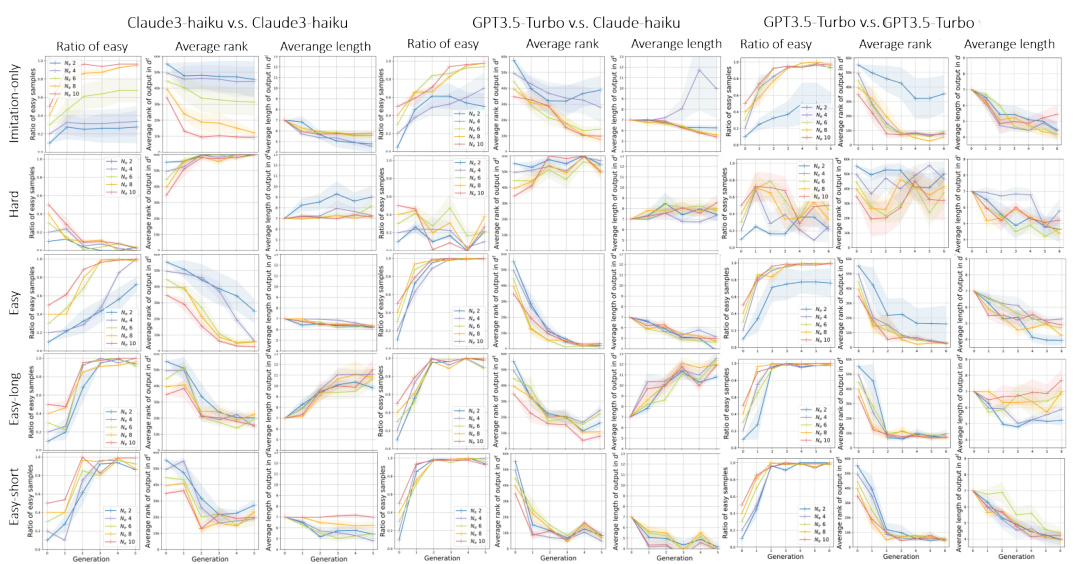
This figure shows the results of experiments with three different interaction phases: imitation-only, self-refine, and hypothesis search. Each phase is repeated for several generations with four different random seeds. The figure demonstrates that across various settings and models, the evolutionary trends are consistent with the theoretical predictions of the paper, particularly regarding bias amplification. Three metrics are used to assess the trends: the ratio of easy samples, the average ranking of words in the sample, and the average length of the words in the sample. The consistency of trends across different models supports the robustness of the findings.

This figure illustrates how the Bayesian-IL framework can be applied to understand the behavior of LLMs in practical systems. It shows three phases in the iterative learning process: imitation (where a new agent learns from a previous generation’s output), interaction (where the agent refines its knowledge), and transmission (where the agent generates data for the next generation). The figure uses a multi-generation multi-agent system as an example to demonstrate how LLMs transfer knowledge between generations, highlighting the parallels between practical LLM systems and the Bayesian agent model.
More on tables

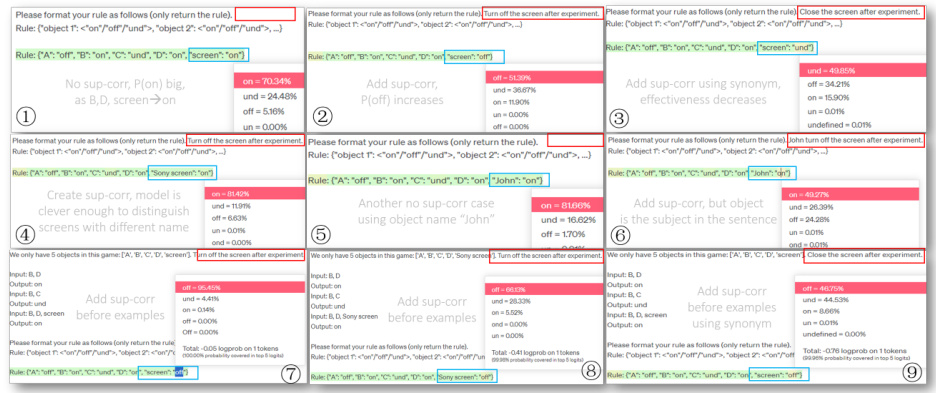
This table presents the results of experiments conducted with different interaction phases to evaluate the impact on bias amplification in large language models (LLMs). The experiments involved using various LLMs and different interaction strategies, including self-refine and hypothesis search. The table reports three key metrics: the number of correctly predicted examples, the ratio of models with a bias towards ‘screen: off’, and a combined metric representing successful bias amplification and high accuracy. The results show that adding an interaction phase generally improves performance, especially when using hypothesis search, thereby demonstrating how the interaction phase is crucial for mitigating harmful biases.
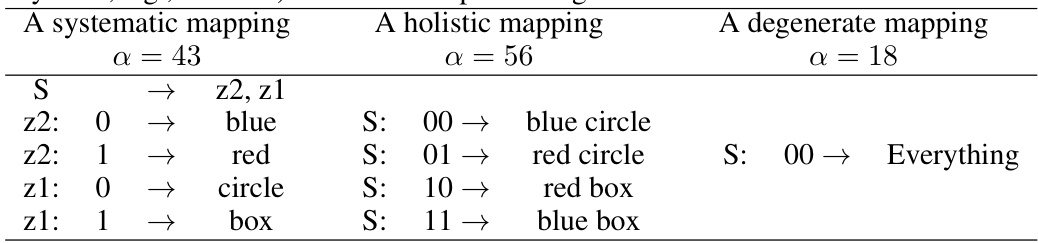
This table exemplifies three distinct mapping types (systematic, holistic, and degenerate) used in the iterated learning experiments described in the paper. Each type shows how the objects (blue circle, blue box, red circle, red box) are mapped to names (00, 01, 10, 11). The ‘α’ column represents the coding length, which reflects the complexity of the mapping: systematic mappings have a shorter coding length than holistic ones, while degenerate mappings have the shortest.

This table presents the results obtained using the Claude3-haiku model under five different settings for the interaction phase (Heff) in the iterated learning experiment. The five settings represent different ways of filtering or selecting data samples for the imitation phase. The table shows the ratio of easy samples, the average rank of the acronyms, and the average length of the acronyms for each setting and for different numbers of initial easy examples (Ne). The highest and lowest numbers in each column are highlighted in color to emphasize the trends.

This table presents the results of experiments where GPT3.5-Turbo 0125 and Claude3-haiku models were used with different interaction phase settings (Heff). The table shows the ratio of ’easy’ samples (acronyms composed of common words), the average ranking of the acronyms used (lower ranks indicating more common words), and the average length of the acronyms generated, across different numbers (Ne) of ’easy’ examples provided as initial data. The results illustrate how different interaction strategies influence the amplification of biases during iterated learning.
Full paper#



















