A Non-parametric Direct Learning Approach to Heterogeneous Treatment Effect Estimation under Unmeasured Confounding

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on causal inference and heterogeneous treatment effects, particularly in scenarios with unmeasured confounding. It provides novel estimators that are more efficient and robust to model misspecification than existing methods, and offers a generalizable framework applicable across various fields. This opens doors for further research into more flexible learning methods within this framework and the exploration of optimal treatment regimes with unmeasured confounding.

Visual Insights

#

This figure is a directed acyclic graph (DAG) illustrating the causal relationships between variables in a scenario with unmeasured confounding and an instrumental variable (IV). The variables include: * X: Observed pre-treatment covariates. * Z: Instrumental variable (IV). * U: Unobserved confounder (latent variable). * A: Treatment assignment. * Y: Outcome. The arrows indicate causal effects. For example, X has a direct causal effect on A and Y, and Z has a direct effect on A. U influences both A and Y, representing unmeasured confounding. Z is selected as an instrumental variable because it is associated with A but is not directly affected by U or Y, providing a path to identify the effect of A on Y even in the presence of the unobserved confounder.

This table presents the results of a simulation study comparing different methods for estimating heterogeneous treatment effects. The methods compared include the proposed IV-DL framework (with and without residualization), Inverse Probability Weighting with Multiple Robustness (IPW-MR), Bayesian Additive Regression Trees (BART), Robust Direct Learning (RD), Causal Forest with IV (CF), and MRIV. Three metrics are reported: Mean Squared Error (MSE) of Conditional Average Treatment Effect (CATE) estimation, Accuracy Rate (AR) of optimal Individualized Treatment Regime (ITR) estimation, and the Value of the estimated ITR. Results are shown for two settings: one with a linear CATE and another with a non-linear CATE.

In-depth insights

#

IV-DL Framework

#

The IV-DL framework, integrating Instrumental Variables (IVs) with Direct Learning (DL), offers a novel approach to estimating Conditional Average Treatment Effects (CATE) in the presence of unmeasured confounding. Its strength lies in directly modeling the heterogeneous treatment effect, bypassing the need for accurate specification of conditional outcome models, a common weakness of traditional methods. The framework leverages the IV to address unmeasured confounding by identifying a causal relationship between treatment and outcome that is not affected by unseen factors. This makes it robust to model misspecification. The introduction of efficient and robust estimators through residualization further enhances the framework’s practical utility, leading to improved efficiency and reduced sensitivity to misspecified nuisance parameters. The framework’s flexibility allows for diverse machine learning models, providing adaptability to various data structures and complexities. However, a potential limitation arises from the need for a valid and relevant IV, a challenge inherent in many observational studies. The framework’s performance, as demonstrated in simulations and real-world data analysis, suggests its potential as a powerful tool in causal inference under challenging conditions. The impact of misspecified nuisance parameters is explored, emphasizing the robustness features of the IV-DL framework.**

Robust Estimators

#

The concept of robust estimators is crucial in statistical modeling, particularly when dealing with real-world data which is often subject to noise, outliers, and model misspecifications. Robust estimators are designed to be insensitive to deviations from assumptions, such as normality or linearity, providing more reliable and stable estimates. In the context of treatment effect estimation, robustness becomes even more critical, as the presence of unmeasured confounders or model misspecification can lead to severely biased results. The research paper explores various methods of achieving robust CATE (Conditional Average Treatment Effect) estimation, possibly including residualization techniques that remove the influence of confounding variables or methods that utilize instrumental variables (IV) to adjust for unmeasured confounding. By residualizing the outcome, the impact of possibly misspecified nuisance parameters is reduced and the efficiency of estimation is improved. The key advantage is that robust estimators can provide reliable inferences even if some model assumptions are violated, making them a practical and important tool for causal inference in domains with complex data structures.

Simulation Studies

#

A robust simulation study is crucial for validating the proposed method. The design should encompass various scenarios, testing the method’s performance under different conditions. Key aspects to consider include sample size, the presence and strength of unmeasured confounding, and the characteristics of the instrumental variable. Furthermore, a comparison with existing methods is essential to demonstrate improvements or highlight limitations. The metrics used to evaluate performance should be clearly defined and relevant to the research question. The selection of these metrics will depend on the specific goals of the research paper, but commonly used metrics might include the mean squared error (MSE) for CATE estimation, and the correct classification rate for optimal ITR estimation. Reporting both point estimates and standard errors or confidence intervals is crucial to gauge the variability and uncertainty associated with the results. The results should be thoroughly discussed, highlighting strengths and limitations in the context of the simulation design and assumptions.

Real Data Analysis

#

A real data analysis section in a research paper is crucial for demonstrating the practical applicability and impact of the proposed methodology. It allows researchers to showcase how their approach performs on real-world data, revealing its strengths and limitations in an environment beyond the controlled setting of simulations. A thoughtful real data analysis will carefully select a relevant dataset, ensuring it aligns with the research questions and the assumptions of the model. The analysis must clearly define the variables, including the treatment, outcome, and covariates. Crucially, it should justify the chosen dataset and address potential limitations or biases inherent in the data. It is important to present the results transparently and rigorously, reporting appropriate metrics and providing visual aids like charts or graphs to effectively communicate findings. Ideally, the analysis will go beyond simple descriptive statistics, exploring the heterogeneity of treatment effects and providing insights into factors driving these differences. A strong real data analysis section significantly enhances the paper’s impact and credibility, providing valuable evidence supporting the research contributions.

Future Directions

#

Future research could explore extending the IV-DL framework to handle multi-armed and continuous treatments, a significant challenge given the need for modified identification assumptions. Investigating the use of deep neural networks within the IV-DL framework to leverage their expressive power for complex data relationships warrants further study. The impact of extreme weights on estimator stability and bias should be addressed through techniques like robust weighting or regularization. A thorough exploration of the framework’s sensitivity to various forms of model misspecification is crucial, and examining the framework’s performance under different confounding scenarios would provide more robust insights. Finally, further investigation into the theoretical and practical implications of the proposed residualization techniques could enhance their efficiency and robustness, and real-world applications could test these methods against other recently developed approaches.

More visual insights

#

More on figures

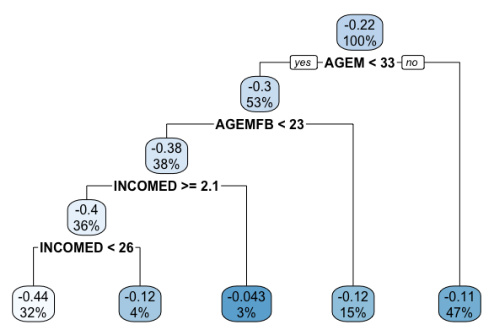
This figure shows a tree-based model for visualizing heterogeneity in conditional average treatment effects (CATE). The tree uses pre-treatment covariates (mother’s age at census, age at first birth, and father’s income) to predict CATE. Each leaf node represents a subgroup of the population with a specific range of covariate values and a corresponding average treatment effect estimate. The numbers in each leaf node represent the estimated CATE and the percentage of the population in that subgroup. The tree shows that there are different subgroups with different treatment effects.

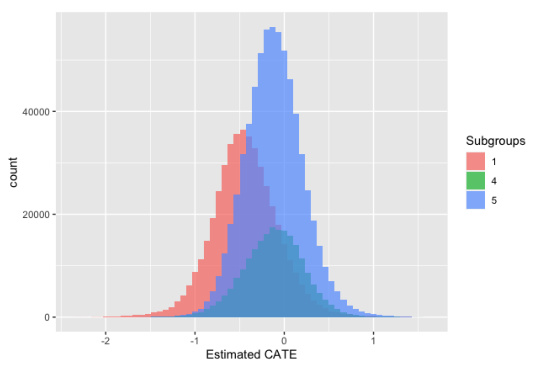
This figure presents histograms visualizing the distribution of estimated Conditional Average Treatment Effects (CATE) for three major subgroups identified in the analysis of mother’s labor force participation. Each histogram shows the frequency of different CATE values within each subgroup. The subgroups are determined by a combination of factors such as mother’s age at census, age at first birth, and father’s income. The visualization helps to understand the heterogeneity of treatment effects across different groups within the population.

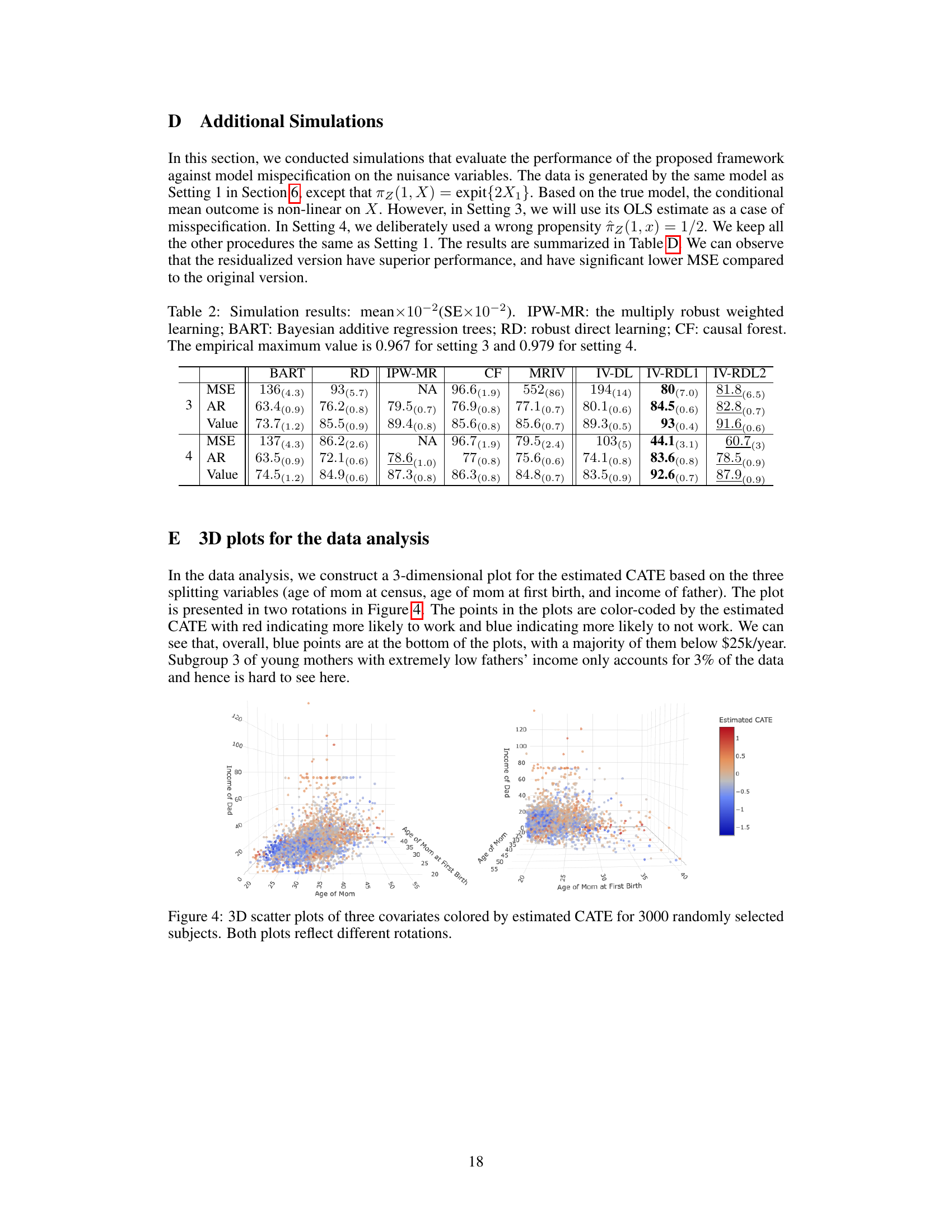
This figure presents 3D scatter plots visualizing the estimated Conditional Average Treatment Effect (CATE) based on three covariates: mother’s age at census, mother’s age at first birth, and father’s income. The plots use color to represent the magnitude of the estimated CATE, with a color gradient ranging from blue (negative CATE) to red (positive CATE). The two plots show the same data but from different viewing angles (rotations) to better illustrate the three-dimensional relationship between the covariates and the estimated treatment effect. The visualization aims to demonstrate heterogeneity in treatment effects across different subpopulations defined by these three covariates.

Full paper

#