↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Estimating conditional average treatment effects (CATEs) is crucial, especially in personalized settings. However, observational data often suffers from confounding bias, while relying solely on instrumental variables (IVs) can lead to high variance due to weak instruments. Existing methods struggle to effectively combine both data types, particularly when dealing with both low compliance in IVs and unobserved confounding.
This paper introduces a novel two-stage framework to overcome these challenges. The first stage estimates a biased CATE from observational data. The second stage leverages IV data for compliance-weighted correction, effectively utilizing the varying IV strength across covariates. This approach combines the strengths of both datasets while mitigating their weaknesses. The researchers demonstrate this method’s effectiveness through simulations and a real-world application analysis, showcasing its robustness and enhanced accuracy over traditional methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with observational and instrumental variable data, offering robust methods for estimating heterogeneous treatment effects. It directly addresses challenges of weak instruments and unobserved confounding, opening new avenues for research in personalized medicine, digital platforms, and causal inference more broadly.
Visual Insights#
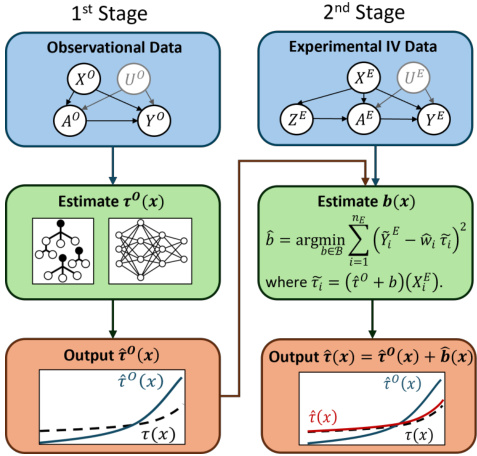
The figure shows a flowchart of the two-stage estimation method. The first stage uses observational data to estimate a biased CATE (τ⁰(x)). The second stage uses instrumental variable (IV) data to estimate the bias (b(x)) and correct the biased CATE to obtain an unbiased estimate of the CATE (τ(x)). The figure visually represents how the two datasets are integrated to improve estimation accuracy.

This table lists the hyperparameters used for the Random Forest and Neural Network models in the simulation studies. For Algorithm 1, it shows the settings for both the compliance and outcome models (Random Forest). For Algorithm 2, it details the hyperparameters of the neural network used for representation learning and CATE estimation. The hyperparameter choices were made based on established practices in machine learning and prior work on similar datasets, aiming for a balance between model complexity and computational efficiency.
In-depth insights#
CATE Estimation#
The paper delves into the estimation of Conditional Average Treatment Effects (CATEs), a crucial task in causal inference, focusing on scenarios with unobserved confounding and weak instrumental variables (IVs). A two-stage approach is proposed: initially, a biased CATE estimate is derived from observational data, then this bias is corrected using IV data, specifically leveraging the variability in IV strength across different covariates. This approach cleverly combines the strengths of observational data and IVs, mitigating the limitations of relying solely on either data source. The key innovation lies in the compliance-weighted correction technique, which effectively addresses low compliance and even situations with zero compliance in subgroups. Theoretical convergence rates for the proposed method are analyzed, and its efficacy is validated through simulations and a real-world application on 401(k) plan participation data. The approach’s robustness to different bias extrapolation techniques—parametric and representation learning—is also explored.
Two-Stage Framework#
The proposed two-stage framework offers a novel approach to estimating Conditional Average Treatment Effects (CATEs) by cleverly combining observational data and instrumental variable (IV) data. The first stage leverages observational data to obtain an initial, albeit biased, estimate of the CATE. This is crucial as it addresses the inherent challenge of unobserved confounding in observational studies. The second stage then employs IV data, often containing low compliance, to correct the bias in the initial CATE estimate. This is achieved through a compliance-weighted correction, effectively mitigating the effects of weak instruments. The framework’s strength lies in its ability to handle varying IV strength across different subgroups, including scenarios where some subgroups may exhibit zero compliance. This adaptability is a significant advancement over traditional methods which often struggle with weak or non-uniform compliance. The use of compliance weighting and the two-stage approach provide robustness to the weaknesses inherent in relying solely on either observational or IV data alone. The framework is further enhanced by offering two distinct methods for extrapolating the bias function, namely a parametric approach and a transfer learning strategy, each with distinct strengths depending on the data’s characteristics and assumptions.
Bias Extrapolation#
The concept of “Bias Extrapolation” in causal inference, particularly within the context of combining observational and instrumental variable (IV) data, is crucial. It addresses the challenge of estimating unbiased conditional average treatment effects (CATEs) when dealing with low IV compliance or weak instruments. The core idea is to leverage observational data to initially estimate a biased CATE, and then use the IV data to learn and extrapolate the bias function. This extrapolation is key because the IV may only be informative for certain sub-populations. The method effectively transfers knowledge about the bias from regions where the IV is strong to areas of weak or zero compliance, leading to more robust and reliable CATE estimates across the entire covariate space. Two main approaches are presented in this research: parametric extrapolation (assuming a specific form for the bias) and a transfer learning approach (assuming a shared representation between the true and biased CATEs). The success of bias extrapolation heavily depends on the validity of the underlying assumptions, particularly the ability to reliably model the relationship between observed and unobserved confounders. The method’s strength lies in its ability to synthesize information from two data sources to address limitations inherent in each individually. However, careful consideration of the limitations and potential biases associated with weak instruments and observational data remains critical for accurate and reliable causal inference.
Real-World Impact#
This research significantly impacts the real world by offering a robust method for estimating heterogeneous treatment effects, particularly valuable in scenarios with weak instruments and unobserved confounding. Accurate CATE estimations are crucial for evidence-based policymaking and personalized interventions in various fields. The two-stage approach, incorporating both observational and instrumental variable data, enhances the reliability of causal inferences, reducing bias and variance. Applications range from personalized medicine and digital platforms to economic policy, improving decision-making by providing more precise and targeted insights into treatment effect heterogeneity. However, the reliance on several assumptions, including the standard IV assumptions and unconfounded compliance, highlights the need for careful consideration and validation in practical applications. The potential for bias due to model misspecification or weak instruments needs careful attention. Furthermore, while offering great promise, the ethical considerations and societal impacts of accurate CATE estimation should be carefully considered before deployment.
Method Limitations#
The proposed methodology, while innovative, relies on several crucial assumptions that, if violated, could significantly impact the validity of the results. Unobserved confounding remains a concern, despite the incorporation of instrumental variables. The effectiveness hinges on the strength of the instruments, with weak instruments potentially leading to biased and high-variance estimates. The assumption of unconfounded compliance requires careful consideration; its violation would directly impact the accuracy of the bias correction. Furthermore, extrapolation of bias from subpopulations with stronger instrument relevance to those with weak or no relevance is a critical step, demanding careful validation. The choice of parametric models or representation learning for bias extrapolation introduces additional limitations, with parametric assumptions being the weakest link. Bias in the estimation of the compliance function could propagate errors, compromising the reliability of the final CATE estimates. Finally, high dimensionality and complex data structures might exacerbate existing limitations, demanding more sophisticated techniques to ensure model stability and generalization.
More visual insights#
More on figures

This figure compares the performance of different methods for estimating conditional average treatment effects (CATEs) using simulated data. It shows the biased observational CATE estimates (2a), high-variance CATE estimates from an instrumental variable (IV) approach (2b), and the CATE estimates from the proposed two-stage method (Algorithm 2) using either parametric extrapolation or representation learning (2c). The results are based on 100 simulated dataset pairs, using Random Forests and Neural Networks as the underlying machine learning models.
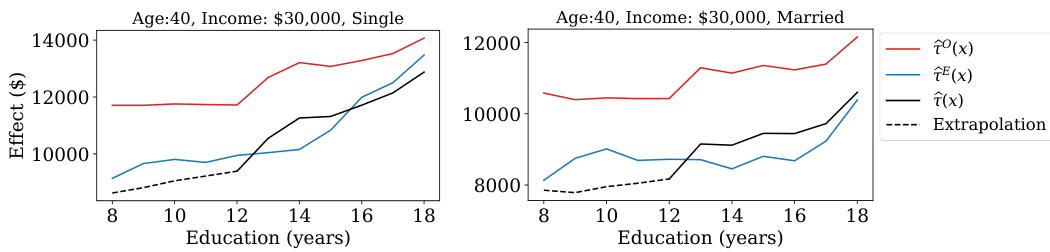
This figure displays the impact of 401(k) participation on net worth, broken down by education level. It shows CATE estimates (conditional average treatment effect) from Algorithm 1, considering age, income and marital status as fixed variables. The black line represents the estimated CATE from Algorithm 1, while the dashed line extrapolates the model’s predictions to the no-compliance region (where individuals are ineligible for 401(k)). The figure compares single and married individuals.
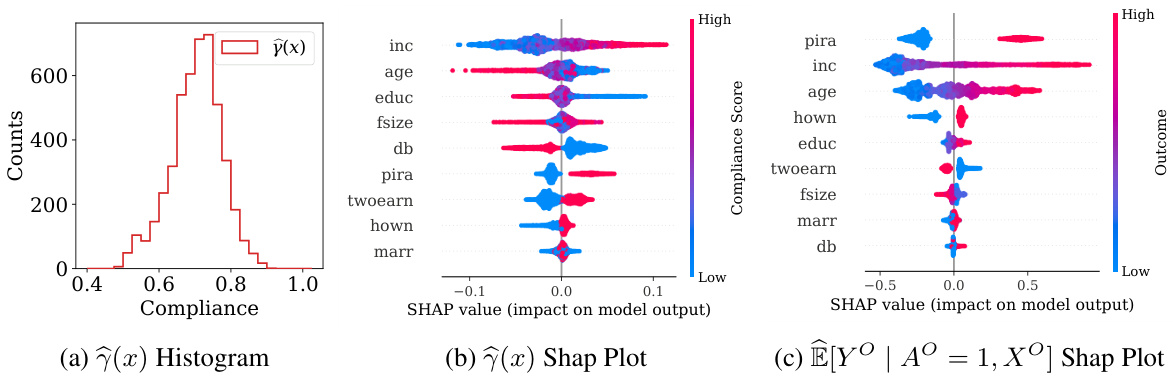
This figure displays the characteristics of the 401(k) dataset used in the paper. Panel (a) shows the distribution of compliance scores, which is a measure of how strongly the instrumental variable (401k eligibility) affects the treatment (401k participation). Panel (b) shows the importance of different features in predicting compliance using SHAP values. Finally, panel (c) shows the importance of features in predicting the outcome (net financial assets) using SHAP values.
More on tables
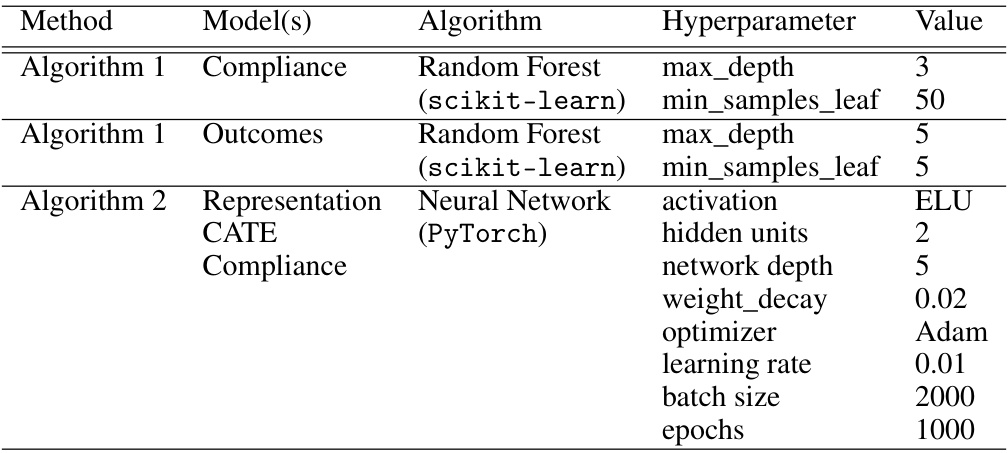
This table lists the hyperparameters used for the Random Forest and Neural Network models in the simulation studies. It breaks down the hyperparameters for both the compliance and outcome models used in the two algorithms. The Random Forest parameters include max_depth and minimum samples per leaf. The Neural Network hyperparameters include activation function, number of hidden units, network depth, weight decay, optimizer, learning rate, batch size and number of epochs.
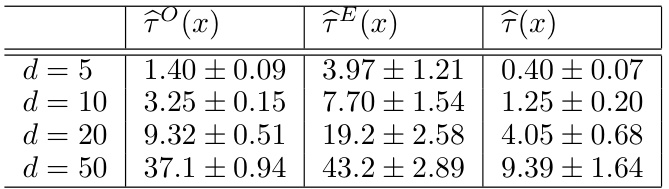
This table presents the mean squared error (MSE) and standard deviation (SD) for three different CATE estimators in a high-dimensional data generating process (DGP). The estimators are: the biased observational CATE (τ^O(x)), the high-variance CATE from the IV dataset (τ^E(x)), and the proposed two-stage CATE estimator (τ^(x)). The results are shown for different dimensions (d) of the covariates. The table demonstrates the effectiveness of the two-stage approach in reducing both bias and variance compared to using the observational or IV data alone.
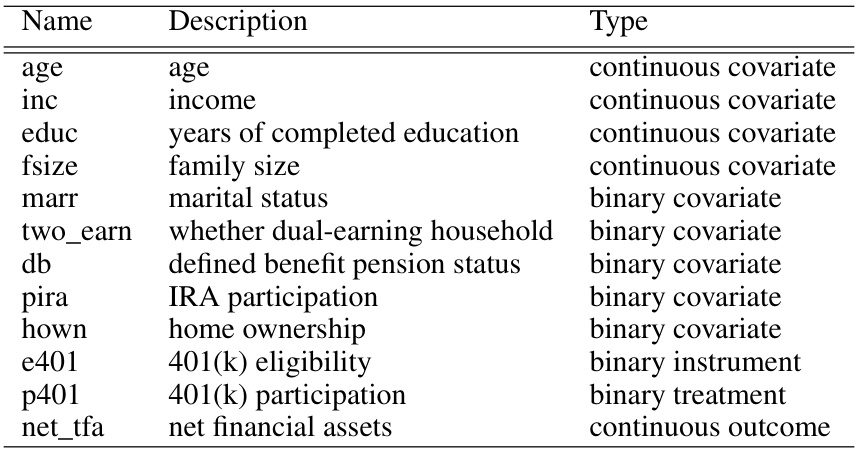
This table lists the names, descriptions, and data types of the variables included in the 401(k) dataset used in the paper’s real-world case study. It shows that the dataset contains a mix of continuous and binary covariates, along with the instrumental variable (401k eligibility), the treatment variable (401k participation), and the outcome variable (net financial assets).
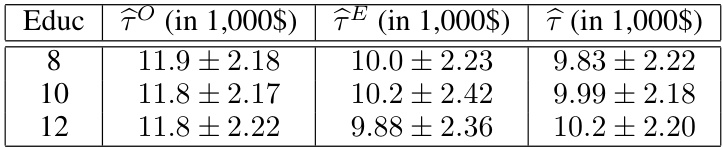
The table shows the mean squared errors (MSE) and standard deviations (SD) for three different estimators of the conditional average treatment effect (CATE) across 100 different random splits of the 401(k) dataset. The estimators are: the biased observational CATE (τ^O), the high-variance IV CATE (τ^E), and the proposed two-stage corrected CATE (τ^). The results are presented for three different education levels (8, 10, and 12 years), holding age and income constant. The table illustrates the effectiveness of the proposed method in reducing both bias and variance.
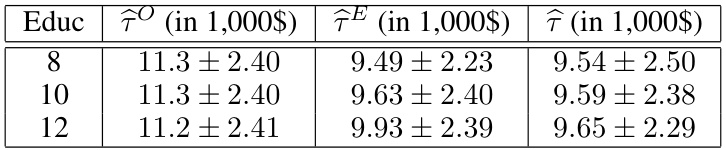
This table presents the Mean Squared Error (MSE) and Standard Deviation (SD) of the CATE estimates obtained from three different estimators across 100 different data splits. The estimators are: biased observational CATE (τO), CATE from IV data alone (τE), and the proposed method combining observational and IV data (τ̂). Results are shown for three different education levels (8, 10, 12 years). The table highlights the improved accuracy of the proposed method compared to the other two approaches, particularly in terms of reduced MSE.
Full paper#



















