↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Diffusion models show promise in reinforcement learning (RL) due to their ability to model complex distributions. However, their high computational cost at inference time (sampling) hinders broader applications. Existing diffusion-based RL methods often struggle with slow inference and planning challenges, particularly in balancing exploration and exploitation. The inherent flexibility of diffusion models also presents difficulties in implementing efficient exploration strategies.
This research introduces Diffusion Spectral Representation (Diff-SR), a novel framework that leverages the connection between diffusion models and energy-based models. Diff-SR bypasses the sampling bottleneck by directly learning value function representations. The approach facilitates efficient policy optimization and practical algorithms, delivering robust performance across various benchmarks. The effectiveness is validated through comprehensive empirical studies in both fully and partially observable settings, showcasing significant improvements over existing methods in terms of both performance and computational efficiency.
Key Takeaways#
Why does it matter?#
This paper is crucial for RL researchers seeking efficient and robust methods. It offers a novel approach to leverage diffusion models without the computational burden of sampling, opening new avenues for exploration and tackling the limitations of existing diffusion-based RL algorithms. This work is highly relevant to current trends in representation learning and spectral methods for RL, providing both theoretical justifications and strong empirical evidence of its benefits.
Visual Insights#

This figure compares the performance of the proposed Diff-SR algorithm against several baseline methods on four MuJoCo locomotion tasks from the MBBL benchmark. The x-axis represents training steps, while the y-axis shows the average return achieved by each algorithm. Shaded areas indicate the standard deviation across four independent runs with different random seeds, providing a measure of variability. The plot allows for a visual comparison of the learning speed and overall performance of Diff-SR relative to other model-based and model-free reinforcement learning approaches.
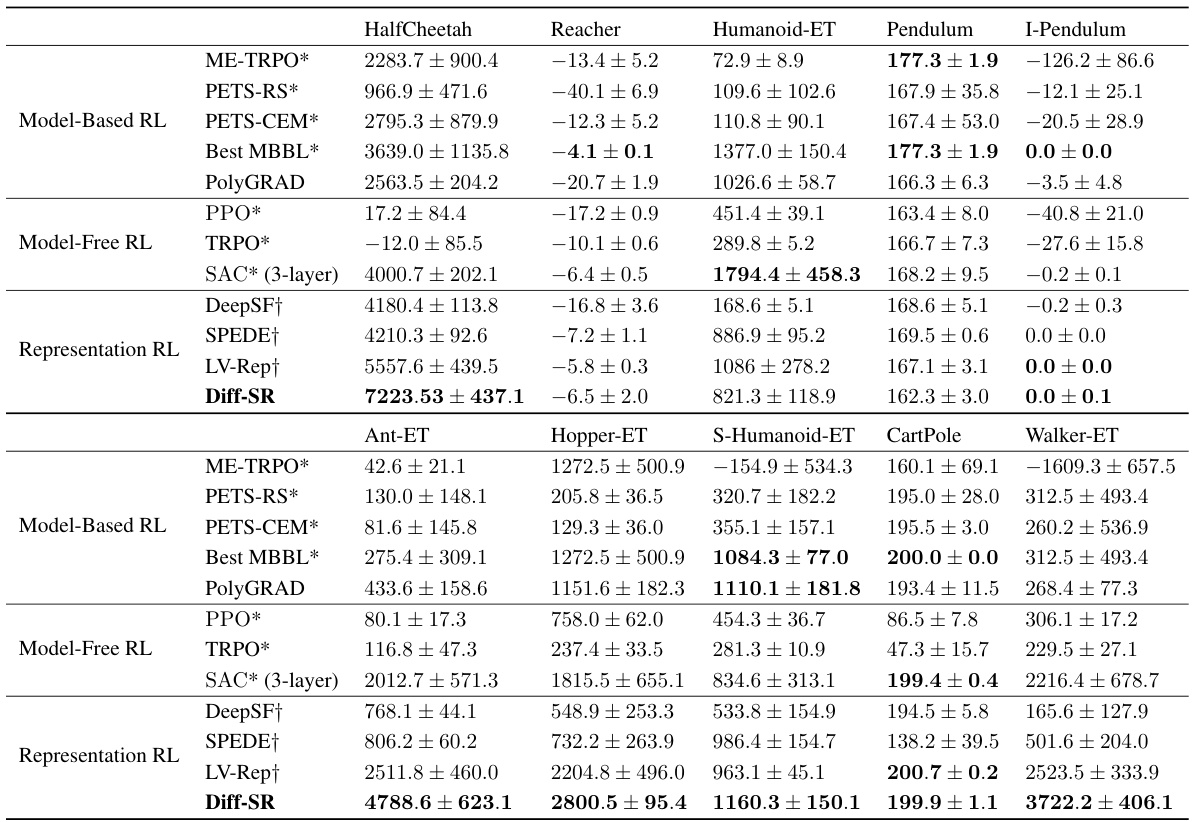
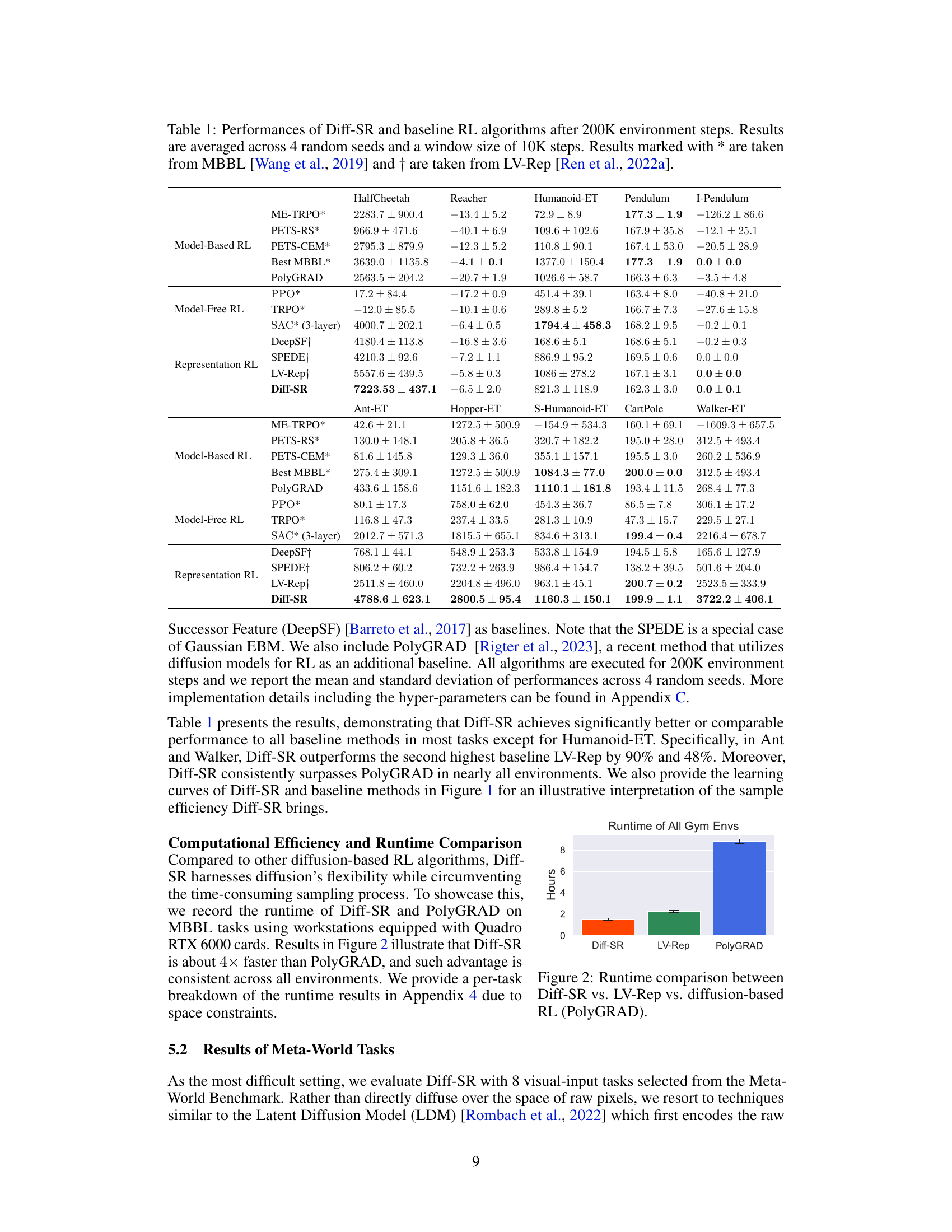
This table presents the performance comparison between Diff-SR and various baseline reinforcement learning algorithms (model-based, model-free, and representation learning methods) across multiple continuous control tasks from the Gym-MuJoCo locomotion benchmark. The results are averaged across four random seeds and a 10K step window after running for 200K environment steps. The table highlights Diff-SR’s performance relative to existing methods.
In-depth insights#
Diff-SR: A New RL Approach#
Diff-SR presents a novel approach to reinforcement learning (RL) by leveraging the representational power of diffusion models without the computational burden of direct sampling. It cleverly shifts focus from generative modeling to representation learning, extracting spectral features from the diffusion process to efficiently represent value functions. This bypasses the slow sampling inherent in many diffusion-based RL methods, significantly improving efficiency. By exploiting the energy-based model perspective of diffusion models, Diff-SR establishes a robust framework for both fully and partially observable Markov Decision Processes (MDPs and POMDPs). The algorithm demonstrates promising empirical results across various benchmarks, showcasing superior performance and computational efficiency compared to existing techniques. The core innovation lies in its ability to learn sufficient representations for policy optimization and exploration without the need for sample generation, addressing a major limitation of previous diffusion-based RL approaches. Diff-SR’s ability to handle both fully and partially observable environments highlights its versatility and potential for broader real-world applications.
Efficient Spectral Learning#
Efficient spectral learning methods aim to speed up the learning process in spectral domains. Traditional spectral methods often involve computationally expensive matrix operations, limiting their scalability and applicability. Efficient techniques leverage various optimization strategies like low-rank approximations and randomized algorithms to reduce computational complexity, making them suitable for large-scale datasets. Careful feature engineering and selection of appropriate kernels are also crucial for maximizing the efficiency and accuracy of the methods. Addressing overfitting is a key challenge, necessitating regularization strategies. Specific applications in areas like reinforcement learning and graph analysis benefit greatly from such advancements.
Energy-Based Model View#
The concept of an Energy-Based Model (EBM) offers a powerful lens through which to analyze diffusion models. EBMs directly model the probability density function of data by defining an energy function that relates to the likelihood. This provides an alternative perspective to the more common Markov chain view of diffusion models, which focuses on the iterative denoising process. The EBM interpretation highlights the inherent connection between diffusion models and spectral representations, as the energy function can be linked to a kernel that has a spectral decomposition. This connection proves valuable in reinforcement learning, facilitating the efficient extraction of spectral features for value function approximation without the computational burden of repeated sampling from the diffusion model. By leveraging the EBM framework, the algorithm can bypass the slow sampling process inherent in traditional diffusion models while retaining the expressiveness of the model for representing complex value functions. This makes the EBM view crucial for bridging the gap between the theoretical elegance of diffusion models and the practical demands of reinforcement learning, offering a path toward more efficient and scalable algorithms.
Empirical Performance Gains#
An analysis of empirical performance gains in a research paper would require access to the paper itself. However, considering the topic, a discussion of empirical performance gains would focus on quantifiable improvements shown by the proposed method compared to existing baselines or alternative approaches. This might involve metrics such as accuracy, efficiency, or robustness, measured across various datasets and experimental conditions. A thorough analysis would delve into the statistical significance of these gains, addressing whether observed improvements are likely due to chance or represent a genuine advancement. Furthermore, a discussion should address potential confounding factors, and explore whether observed gains are consistent across different scenarios and datasets. Finally, a thoughtful analysis must emphasize the practical implications of these gains, highlighting the real-world impact of the study and the potential to translate the findings into useful applications.
Future Research: POMDPs#
Extending the proposed Diff-SR framework to handle Partially Observable Markov Decision Processes (POMDPs) presents a significant and exciting avenue for future research. POMDPs are more realistic models for many real-world problems, where an agent doesn’t have access to the complete state. The core challenge lies in adapting the spectral representation learning to scenarios with hidden state information and potentially noisy observations. One promising approach would involve designing a mechanism to effectively represent the belief state, which encapsulates the agent’s uncertainty about the true state given its observations. This could potentially involve integrating techniques from recursive Bayesian estimation or other belief state representation methods. Exploring different architectures for approximating the belief state is crucial, balancing model complexity and computational efficiency. Furthermore, investigating efficient exploration strategies within the POMDP setting would be essential, as the uncertainty associated with the hidden state makes exploration significantly harder. Developing theoretically sound exploration algorithms that complement Diff-SR’s representation learning would greatly enhance its practical applicability in challenging POMDP domains. Finally, extensive empirical evaluation on various benchmark POMDP tasks, potentially involving complex state and observation spaces, is needed to demonstrate the robustness and effectiveness of the extended Diff-SR in realistic scenarios.
More visual insights#
More on figures
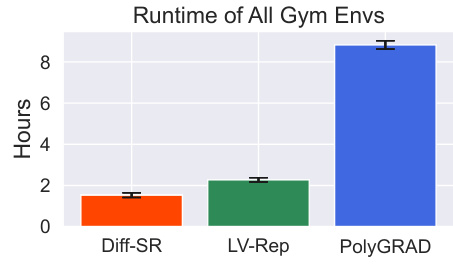
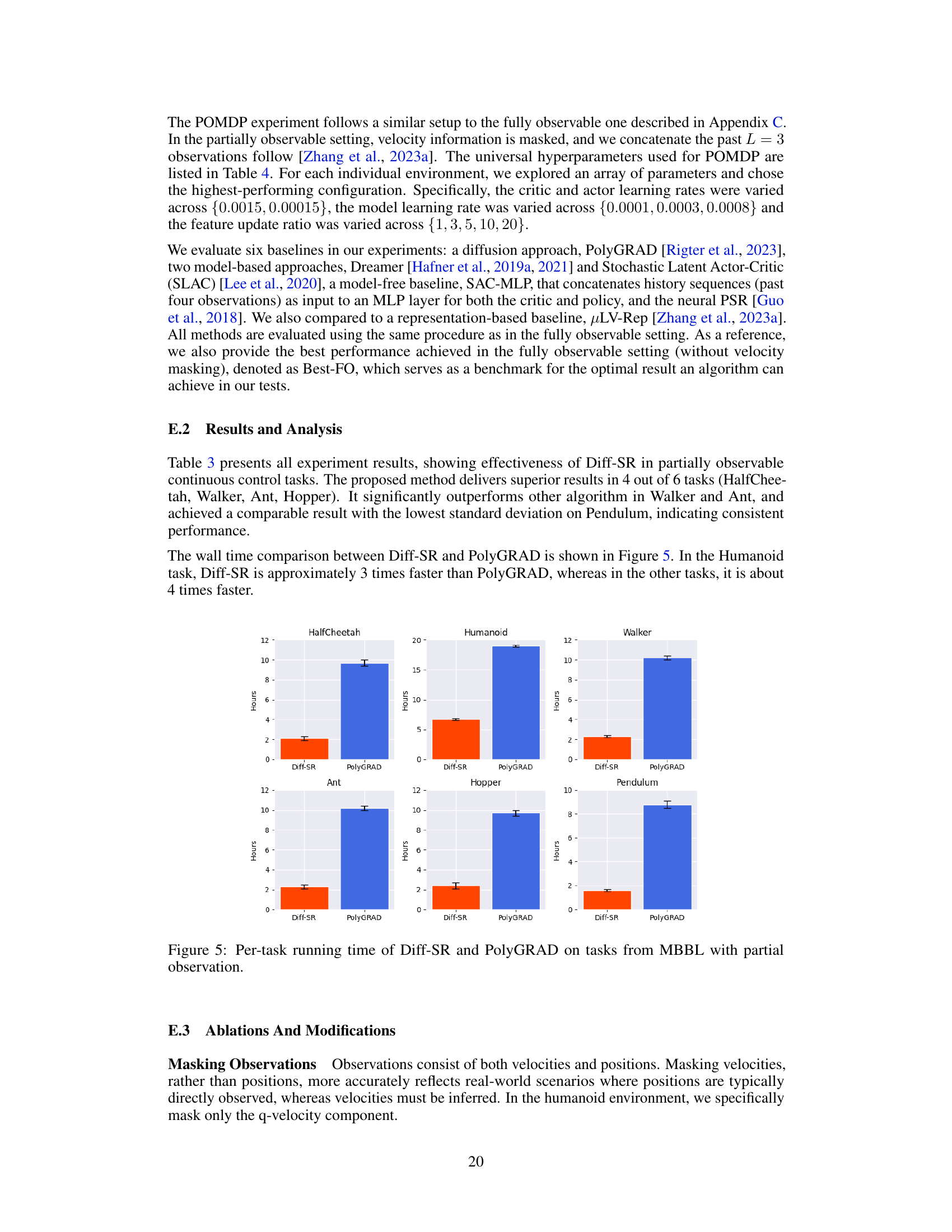
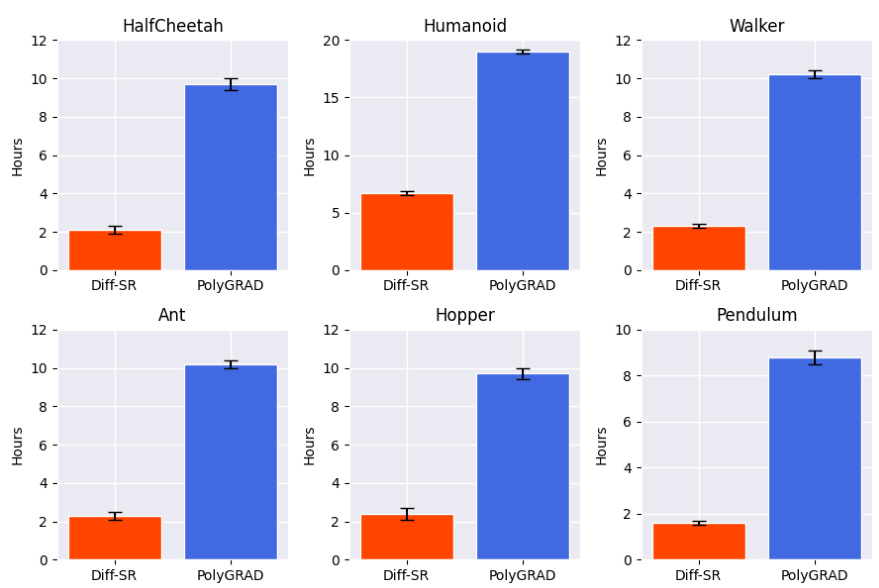
This figure shows a bar chart comparing the runtime of three reinforcement learning algorithms: Diff-SR, LV-Rep, and PolyGRAD. The runtime is measured in hours across all the Gym MuJoCo locomotion environments. Diff-SR shows significantly shorter training time than the other two algorithms, demonstrating its computational efficiency.

This figure shows the learning curves for eight different image-based partially observable Markov decision process (POMDP) tasks from the Meta-World benchmark. Each curve represents the success rate of a particular reinforcement learning algorithm over the course of training. The algorithms being compared include MWM, µLV-Rep, Dreamer-v2, DrQ-v2, and Diff-SR. The shaded area around each curve indicates the standard deviation across five different random seeds, giving a sense of the variability in performance. The x-axis represents the number of environment steps, and the y-axis represents the success rate (in percent).

This figure compares the performance of the proposed Diffusion Spectral Representation (Diff-SR) method against several baseline reinforcement learning algorithms across multiple MuJoCo locomotion tasks from the MBBL benchmark. The x-axis represents training steps, and the y-axis represents the average return achieved by each algorithm. The solid lines show the average performance across four different random seeds, while the shaded areas indicate the standard deviation, giving a measure of the variability of the results. This visualizes the learning curves and allows for a comparison of the sample efficiency and overall performance of Diff-SR relative to other methods.
This figure compares the performance of Diff-SR against several baseline methods across multiple MuJoCo locomotion tasks from the MBBL benchmark. The x-axis represents training steps, while the y-axis shows the reward obtained. Each curve represents the average reward over four runs, with the shaded area indicating the standard deviation. The figure visually demonstrates Diff-SR’s superior performance and stability compared to other methods like LV-Rep, SAC, and PolyGRAD.

This figure visualizes the process of generating images using the learned score functions from Diff-SR. Starting from a random noise, the model progressively refines the image over multiple steps, eventually reaching a reconstruction that closely resembles the original observation. This demonstrates the ability of the learned score function to capture the underlying data distribution and reconstruct images from noisy latent representations.
More on tables
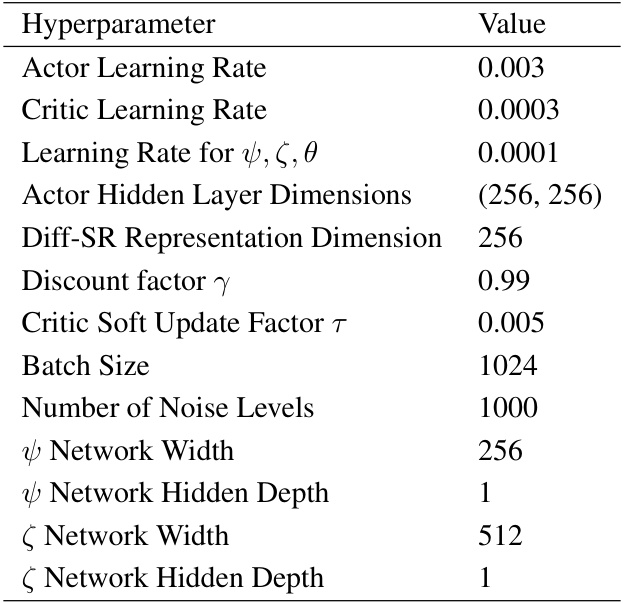
This table presents the performance comparison of Diff-SR against various baseline reinforcement learning algorithms across multiple continuous control tasks from the MuJoCo locomotion benchmark after 200,000 environment steps. The results are averaged across four random seeds, utilizing a window size of 10,000 steps for smoothing. Results from MBBL (Wang et al., 2019) and LV-Rep (Ren et al., 2022a) are also included for comparison.

This table compares the performance of the proposed Diff-SR algorithm against various baseline reinforcement learning algorithms across multiple continuous control tasks from the Gym-MuJoCo locomotion benchmark. The performance metrics are averaged over four random seeds and a 10k step window. The algorithms are categorized into model-based RL, model-free RL, and representation RL methods for better comparison. Asterisks and daggers indicate that the results for certain methods were taken from other papers, referenced in the caption.
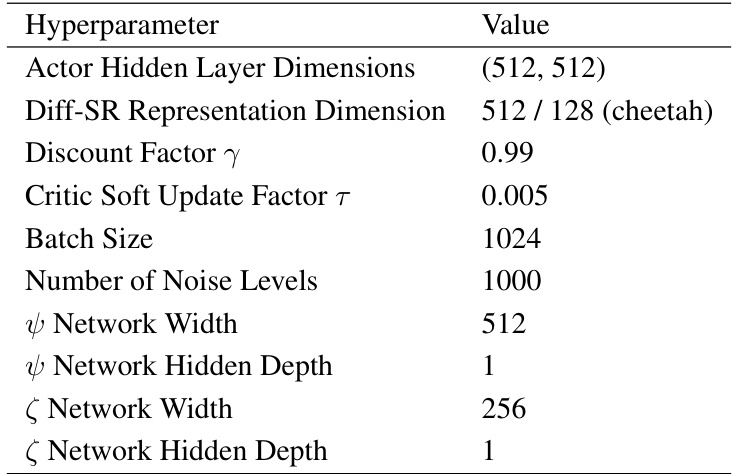
This table lists the hyperparameters used in the experiments for Diff-SR on state-based Partially Observable Markov Decision Processes (POMDPs). It includes settings for the actor and critic networks, the Diff-SR representation, and the training process. Note that the Diff-SR representation dimension is specific to the cheetah environment, while other hyperparameters are generally applicable.
Full paper#