↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world applications involve learning from expert demonstrations. However, these demonstrations might contain contextual information unknown to the learner, leading to suboptimal performance. This paper addresses this issue by proposing a new framework for online sequential decision-making. The key challenge is that expert decisions are based on unobserved factors, while the learner only receives the observable part of the data. This results in a learning problem with unobserved heterogeneity.
Existing methods often struggle in this setting. To address this, the paper introduces Experts-as-Priors (ExPerior), a Bayesian approach using expert data to build an informative prior distribution for the learner’s decision-making process. ExPerior is empirically shown to improve performance across different decision-making setups (multi-armed bandits, Markov decision processes, and partially observable MDPs), outperforming behaviour cloning, online, and online-offline baselines.
Key Takeaways#
Why does it matter?#
This paper is important because it tackles a critical challenge in online sequential decision-making by effectively utilizing expert demonstrations, even with unobserved heterogeneity. It offers a novel Bayesian approach that surpasses existing methods, opening new avenues for research in various applications such as self-driving cars, healthcare, and finance. The proposed algorithm (ExPerior) is shown to improve performance across different decision-making frameworks (bandits, MDPs, POMDPs), making this research broadly relevant and impactful.
Visual Insights#

This figure illustrates the three steps of the Experts-as-Priors (ExPerior) algorithm in a goal-oriented task. Step 1 shows experts demonstrating policies while observing unobserved contextual variables (goals). Step 2 shows how an informative prior distribution is learned from expert data that does not include the goals. Step 3 shows how this prior guides an online Bayesian RL agent to use the learned distribution to perform posterior sampling and select actions in an environment where the goal is unknown.

This table presents the average reward per episode obtained in the Frozen Lake environment (partially observable Markov decision process) after 90,000 training steps. It compares the performance of several algorithms, including ExPerior-MaxEnt and ExPerior-Param (the authors’ proposed algorithms), a Naïve Bootstrapped Deep Q-Network (DQN) baseline, and the EXPLORE algorithm. The results are broken down by the number of hazards on the frozen lake map (5, 7, and 9), and the competence parameter (beta) of the expert policy used to train ExPerior. The ‘Optimal’ row shows the maximum achievable average reward.
In-depth insights#
Unobserved Heterogeneity#
The concept of ‘Unobserved Heterogeneity’ highlights a critical challenge in machine learning, particularly in scenarios involving expert demonstrations. It acknowledges that experts often utilize contextual information unavailable to the learning agent, making direct imitation problematic. This hidden information, or heterogeneity, introduces variance between expert decisions and the learner’s optimal strategy. The paper addresses this by modeling the problem as a zero-shot meta-reinforcement learning task, where the unobserved variables are treated as parameters with an unknown prior. This approach elegantly tackles the difficulty of learning from seemingly disparate expert data by framing it as a meta-learning problem, where the goal is to infer a distribution over the unobserved contexts. The key innovation lies in using expert data to establish an informative prior distribution, which guides exploration in the online learning phase. This method moves beyond traditional approaches, demonstrating the possibility of harnessing expert demonstrations even when crucial contextual information is missing. The paper argues that the uncertainty inherent in unobserved heterogeneity can be effectively addressed by building an informed prior, leading to more efficient and robust online decision-making.
Bayesian Regret#
In the context of online sequential decision-making, Bayesian regret quantifies the cumulative difference between the rewards obtained by an optimal policy (with full knowledge of the underlying data distribution) and the rewards obtained by a learning agent using a specific algorithm. Unlike frequentist regret, which focuses on the expected difference in rewards, Bayesian regret takes a probabilistic perspective, acknowledging the agent’s uncertainty about the environment. This perspective is particularly relevant in settings with unobserved heterogeneity, where the true data distribution is unknown. The paper leverages Bayesian regret to analyze its proposed algorithm’s performance. By modeling unobserved contextual variables as parameters with an unknown prior distribution, the authors frame the problem as Bayesian regret minimization. The analysis aims to demonstrate that the algorithm effectively utilizes expert demonstrations to learn an informative prior, leading to lower Bayesian regret compared to conventional methods. The Bayesian regret is also used to demonstrate a close relationship between the quantity of expert demonstrations and the algorithm’s effectiveness in estimating the optimal policy.
ExPerior Algorithm#
The ExPerior algorithm cleverly tackles the challenge of online sequential decision-making using expert demonstrations, especially when those demonstrations contain unobserved heterogeneity. Its core strength lies in its Bayesian approach, which leverages expert data to construct an informative prior distribution over unobserved contextual variables. This prior is key; it guides the learning process, enabling efficient exploration and exploitation even when the learner is unaware of these hidden factors. ExPerior’s flexibility is notable. It accommodates various decision-making frameworks—multi-armed bandits, MDPs, and POMDPs—demonstrating its wide applicability. The algorithm’s implementation offers two pathways for prior learning: a parametric method utilizing existing knowledge, and a non-parametric approach employing maximum entropy when prior knowledge is lacking. Empirically, ExPerior outperforms existing baselines, showcasing significant improvements in Bayesian regret across diverse settings. The algorithm’s reliance on the entropy of the optimal action to assess the impact of unobserved heterogeneity is particularly interesting, offering a novel way to measure and quantify this effect. Overall, ExPerior represents a significant advance in online decision making, particularly in scenarios involving incomplete or heterogeneous expert guidance.
Empirical Evaluation#
An empirical evaluation section in a research paper is crucial for validating the claims made. It should meticulously detail the experimental setup, including datasets used, metrics employed, and baselines compared against. Rigorous methodology is essential, specifying how data was split, hyperparameters tuned, and statistical significance assessed. Transparency is key; the reader needs to understand how results were obtained to judge their validity. The discussion of results should go beyond simply reporting numbers, interpreting their meaning in relation to the hypothesis and limitations of the study. Visualizations like graphs and tables enhance clarity and understanding. A robust empirical evaluation strengthens the paper’s credibility and increases the impact of the findings.
Future Works#
Future research directions stemming from this work could explore more complex environments beyond the simulated settings used, focusing on real-world applications in domains like robotics or personalized education. Investigating the theoretical properties of the algorithm, particularly its sample complexity and regret bounds under various conditions, would enhance its understanding and applicability. Furthermore, incorporation of human feedback into the learning process could lead to more robust and reliable performance, as human expertise often goes beyond easily quantifiable data. Finally, exploring methods for handling non-stationary environments where the underlying context distribution changes over time would be beneficial for many practical applications. These future studies would enhance the algorithm’s adaptability and broaden its range of use cases.
More visual insights#
More on figures

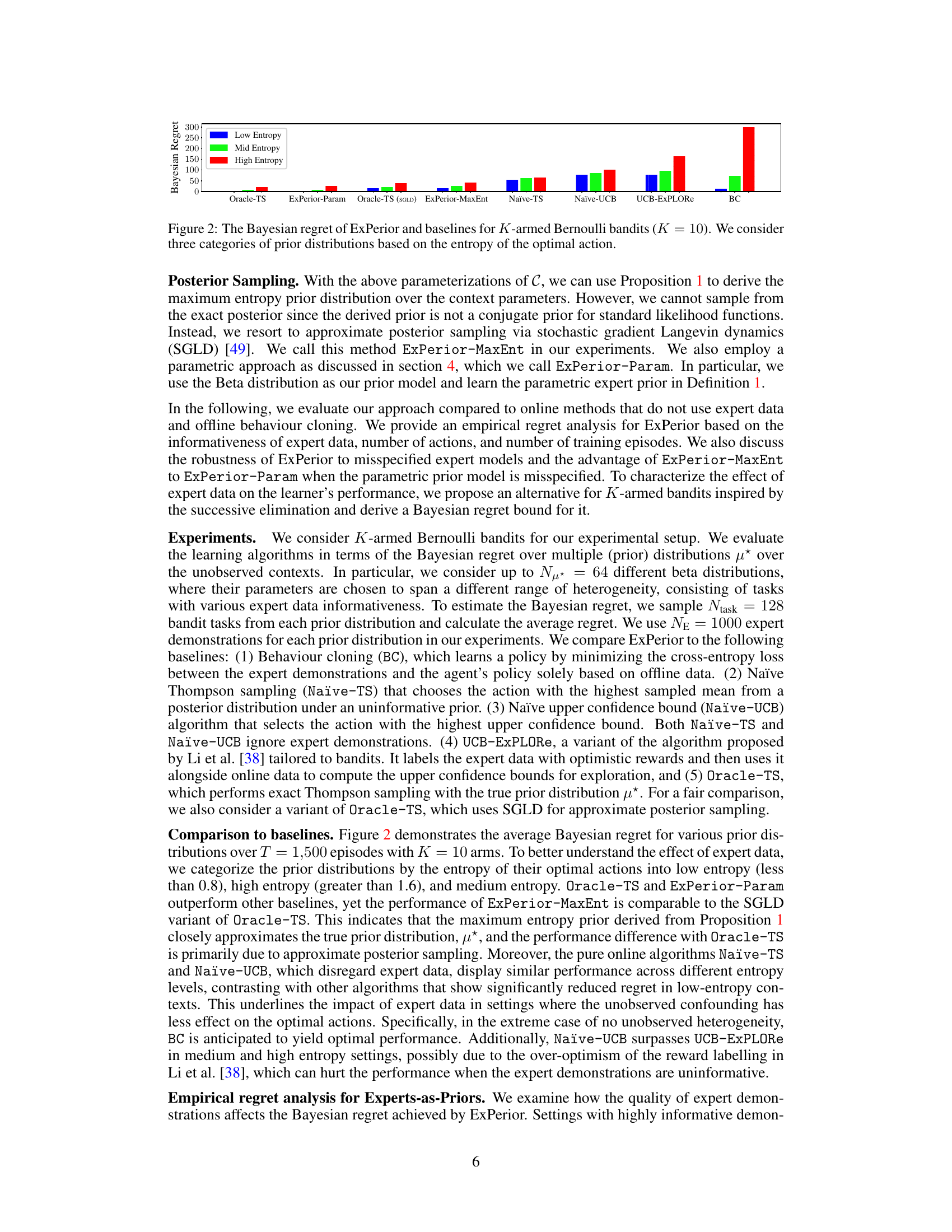
This figure compares the Bayesian regret (a measure of the algorithm’s performance) of different algorithms for solving a multi-armed bandit problem with 10 arms. Each arm has a probability of success (reward) that’s unknown to the algorithm, and the goal is to maximize the cumulative reward over a series of pulls. The algorithms are categorized into three groups based on the entropy of their prior distribution over these unknown probabilities. The x-axis represents the different algorithms including ExPerior, Oracle-TS, and several baselines. The y-axis represents the Bayesian regret. The bars are colored and grouped by entropy level (low, mid, high) to visually show the effect of entropy on regret. The results show that ExPerior achieves the lowest regret across the range of entropy levels.

This figure presents an empirical analysis of the Bayesian regret achieved by the Experts-as-Priors algorithm (ExPerior) in Bernoulli bandit settings. Panel (a) shows three subplots illustrating how the regret changes with the number of arms (K), the entropy of the optimal action, and the number of episodes (T). Panel (b) plots the theoretical regret bound derived in Theorem 2 against the entropy of the optimal action, demonstrating a linear relationship that aligns with the results observed in the middle subplot of panel (a).

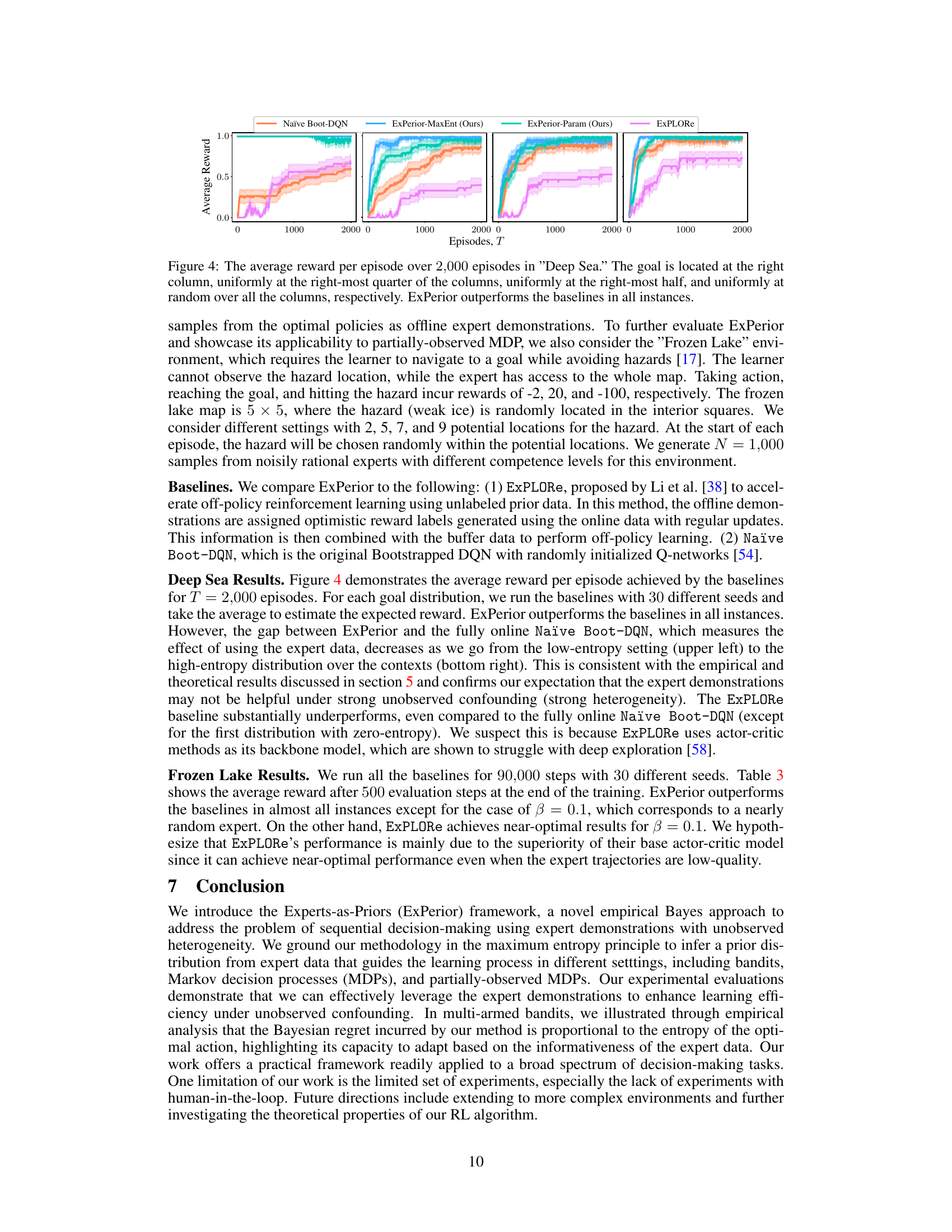
This figure shows the average reward per episode achieved by different reinforcement learning algorithms over 2000 episodes in the Deep Sea environment. The Deep Sea environment is a grid world where the agent starts at the top left and must navigate to a goal at the bottom. The goal’s location varies across four different conditions, with the goal being located at the rightmost column, uniformly at the rightmost quarter of columns, uniformly at the rightmost half of columns, and uniformly at random across all columns. The figure compares the performance of ExPerior (with both maximum entropy and parametric prior approaches) to several baselines, including Naïve Boot-DQN and EXPLORE. The results demonstrate that ExPerior consistently outperforms these baselines across all four goal location distributions.
More on tables
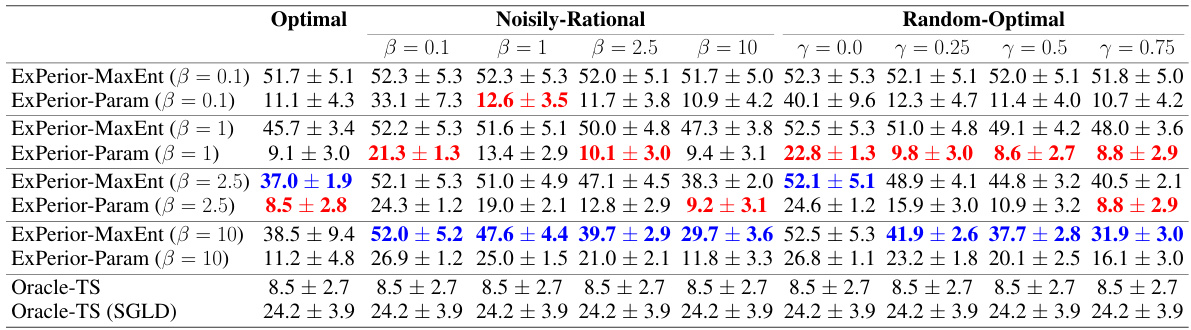
This table presents ablation study results on the robustness of the ExPerior algorithm to different expert model specifications. It compares the performance of ExPerior-MaxEnt and ExPerior-Param under three expert types: optimal, noisily rational, and random-optimal. The random-optimal experts act optimally with a probability γ (varying from 0.0 to 0.75), and randomly otherwise. The results show the effect of the hyperparameter β on the algorithms’ performance across different expert types and levels of optimality.

This table presents the Bayesian regret for different prior distributions (Low, Mid, and High Entropy) using ExPerior-Param and ExPerior-MaxEnt methods with various parametric priors (Gamma, Beta-SGLD, Normal). It also includes results from Oracle-TS, a method with access to the true prior. The results demonstrate that ExPerior-MaxEnt, which employs a non-parametric maximum entropy approach, consistently outperforms ExPerior-Param, particularly when the parametric prior is misspecified. This highlights the robustness and advantage of the non-parametric method in scenarios where prior knowledge is uncertain or inaccurate.

This table presents the average reward per episode achieved by different reinforcement learning algorithms in the Frozen Lake environment after 90,000 training steps. The Frozen Lake environment is a partially observable Markov decision process (POMDP) where an agent needs to navigate to a goal while avoiding hazards. The table compares the performance of ExPerior-MaxEnt, ExPerior-Param, Naïve Boot-DQN, and EXPLORE across different settings with varying numbers of hazards and competence levels (β) of the expert demonstrations. The results show the average reward and standard deviation for each algorithm and setting, indicating the effectiveness of ExPerior in leveraging expert data to enhance performance.
Full paper#