↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Graph Neural Networks (GNNs) are powerful tools for analyzing graph-structured data, but existing methods like Message Passing GNNs (MPGNNs) have limitations. MPGNNs struggle with long-range dependencies in graphs, as information propagation is limited by the number of message-passing steps and the phenomenon of over-squashing, where information is lost during propagation. This restricts their ability to effectively model relationships between distant nodes.
This paper introduces Spatio-Spectral Graph Neural Networks (S2GNNs) to overcome these limitations. S2GNNs cleverly combine spatial and spectral graph filters. This dual approach allows for both local and global information propagation, resolving the long-range dependency issue. The frequency-domain representation of the spectral filter helps avoid over-squashing and enables more efficient information flow. Experiments show that S2GNNs outperform state-of-the-art GNNs on tasks involving long-range interactions.
Key Takeaways#
Why does it matter?#
This paper is highly important for researchers working on graph neural networks (GNNs) and related fields. It introduces a novel GNN architecture that addresses key limitations of existing methods, such as limited receptive fields and over-squashing. The proposed Spatio-Spectral GNN (S2GNN) offers improved performance and scalability, enabling applications to significantly larger graphs. The theoretical analysis and empirical results provide valuable insights into GNN design and performance, potentially influencing future research directions in GNNs. Furthermore, the new design space opened by S2GNNs offers promising new avenues for future investigation.
Visual Insights#
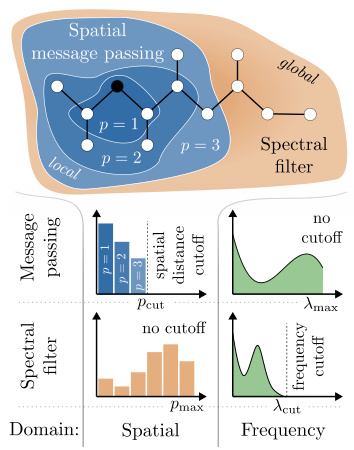
This figure illustrates the core idea of Spatio-Spectral Graph Neural Networks (S2GNNs). It shows how S2GNNs synergistically combine spatial message passing (local and global) with spectral filtering. The left side depicts the spatial message passing process, illustrating the concept of a receptive field that’s limited by the number of hops. The right side shows how a spectral filter operates globally in the frequency domain and can capture long-range interactions, overcoming the limitations of spatial message passing alone. The bottom panels provide visualizations to help understand how spatial and spectral filtering work in both the spatial and frequency domains. The different cutoff parameters for each type of filtering are also highlighted.
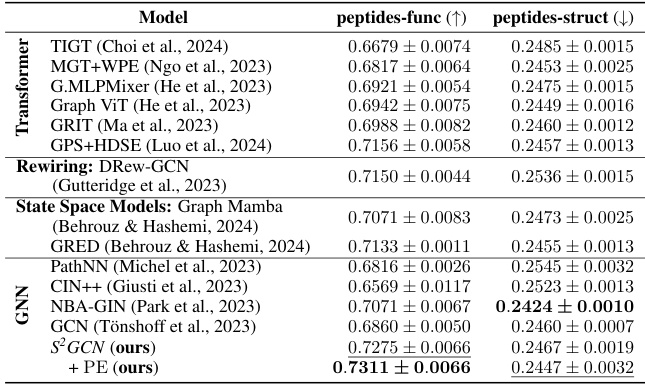
This table compares the performance of S2GCN against various state-of-the-art models on two long-range interaction benchmark datasets: peptides-func and peptides-struct. It shows the accuracy (AP for peptides-func, MAE for peptides-struct) achieved by different types of models (Transformers, Rewiring methods, State Space Models, and other GNNs). The table highlights that S2GCN achieves state-of-the-art performance on peptides-func using significantly fewer parameters than other models.
In-depth insights#
S²GNN: A New Model#
The proposed Spatio-Spectral Graph Neural Network (S²GNN) presents a novel architecture designed to overcome limitations of existing spatial message-passing GNNs. S²GNN synergistically combines spatial and spectral graph filters, leveraging the strengths of both approaches. The spectral component, parametrized in the frequency domain, allows for efficient and global information propagation, addressing the limited receptive field and over-squashing issues inherent in solely spatial GNNs. This combination leads to strictly tighter approximation-theoretic error bounds, implying improved expressiveness. Importantly, S²GNNs allow for free positional encodings, enhancing their expressivity beyond the 1-Weisfeiler-Leman test. Furthermore, the model introduces spectrally parameterized filters for directed graphs, making it applicable to a broader range of graph-structured data. Empirical results demonstrate that S²GNNs outperform spatial MPGNNs, graph transformers, and graph rewirings on various benchmark tasks, showing significant improvements, particularly for long-range interactions. The model scales efficiently to millions of nodes, showcasing its practical applicability. In summary, S²GNN represents a significant advancement in GNN design, effectively blending spatial and spectral information processing for superior performance and scalability.
Spectral Filter Design#
Designing effective spectral filters is crucial for Spatio-Spectral Graph Neural Networks (S2GNNs) to achieve their potential. The choice of parametrization significantly impacts the network’s ability to model long-range interactions and its overall expressiveness. A key design choice involves balancing the filter’s ability to capture global information with computational efficiency. Approaches like using linear combinations of translated Gaussian basis functions offer a flexible yet efficient solution, enabling the network to learn complex spectral patterns. Truncating the frequency spectrum is essential for computational efficiency, but the trade-off between resolution and computational cost needs careful consideration. The use of window functions, such as the Tukey window, can mitigate the Gibbs phenomenon, which is the oscillatory behavior near discontinuities in the spectral representation, ensuring stability. Further exploration into neural network architectures within the spectral domain might provide increased flexibility and expressiveness, but raises the potential challenge of maintaining permutation equivariance. Finally, designing spectral filters for directed graphs requires careful handling of asymmetric adjacency matrices, potentially through use of the Magnetic Laplacian. The overall design process should explicitly consider the approximation-theoretic aspects, with the goal of developing filters that offer superior approximation capabilities compared to spatial filters alone.
Long-Range Modeling#
Long-range modeling in graph neural networks (GNNs) presents a significant challenge due to the inherent limitations of message-passing schemes. Standard GNNs struggle to capture dependencies between distant nodes effectively, often suffering from information decay and over-squashing. This paper addresses this challenge by proposing Spatio-Spectral Graph Neural Networks (S2GNNs), a novel framework that synergistically combines spatial and spectral graph convolutions. The spectral component, parameterized in the frequency domain, allows for efficient global information propagation, overcoming the limitations of solely relying on local spatial interactions. This synergistic combination of local and global information processing enables S2GNNs to achieve superior performance in capturing long-range dependencies on graph-structured data, significantly outperforming existing methods on multiple benchmark tasks. The paper further provides a theoretical analysis, demonstrating that S2GNNs offer tighter approximation-theoretic error bounds than purely spatial MPGNNs and proving they are less susceptible to over-squashing. Furthermore, the introduction of spectrally-parametrized filters for directed graphs broadens the applicability of S2GNNs, opening up new possibilities for long-range modeling in various graph-related domains. The effectiveness and scalability of S2GNNs are validated through extensive empirical evaluations on benchmark datasets, highlighting its potential for handling massive graphs.
Over-Squashing Fix#
Over-squashing, a critical limitation in graph neural networks (GNNs), hinders the propagation of information across long distances within a graph. This phenomenon arises from the repeated application of local aggregation functions, causing information to be compressed and lost. A key focus of many recent GNN advancements is to address this over-squashing problem. Methods proposed in the literature include various architectural modifications, such as incorporating skip connections, using higher-order graph convolutions, and employing attention mechanisms. These techniques aim to improve information flow by allowing direct connections between distant nodes or by weighting node interactions more effectively. Another major approach focuses on enhancing the expressiveness of the GNNs themselves, potentially by using spectral graph convolutions which operate in the frequency domain, thereby facilitating more global information propagation. Combining spatial and spectral approaches is a promising direction that leverages the strengths of both. The ultimate solution to the over-squashing problem likely involves a multi-faceted strategy, combining architectural improvements with more sophisticated aggregation techniques and advanced training methods to effectively capture and utilize long-range dependencies in graph-structured data.
Future Directions#
Future research could explore several promising avenues. Extending S²GNNs to handle dynamic graphs is crucial for real-world applications where graph structure evolves over time. This might involve incorporating temporal information directly into the spectral and spatial filters or developing mechanisms to efficiently update the spectral representation as the graph changes. Investigating the impact of different spectral filter designs on the overall performance of S²GNNs is warranted. Exploring alternative parametrizations, kernel functions, or frequency band selection strategies could lead to further improvements in expressiveness and efficiency. Combining S²GNNs with other advanced GNN techniques, such as graph attention mechanisms or graph transformers, holds the potential for creating even more powerful and versatile graph neural networks. Finally, the scalability of S²GNNs should be further investigated. Developing techniques for training S²GNNs on truly massive graphs, potentially using distributed computing or approximation methods, is essential to expand the applicability of this promising approach.
More visual insights#
More on figures

The figure illustrates the framework of Spatio-Spectral Graph Neural Networks (S2GNNs). It shows how spatial message passing and spectral filters are combined synergistically. The adjacency matrix A and node features X are inputs, and the Laplacian L (derived from A) is used to compute the spectral filter. Positional encodings (PE) are incorporated to enhance expressivity. The framework shows how the spectral filter acts globally on the entire graph (in the frequency domain using eigenvectors of the Laplacian matrix) while the spatial message passing component operates locally (in the spatial domain using the adjacency matrix). This combination of global and local information processing is a key feature of S2GNNs.

This figure illustrates how a spectral filter works as a message-passing mechanism. It shows how the Fourier coefficients (represented by stars) allow nodes to exchange information globally, not just within their immediate neighborhood like in spatial message passing. The width and color of the edges represent the magnitude and sign of the message passing, demonstrating both intra-cluster and inter-cluster communication.

This figure illustrates the core principle of Spatio-Spectral Graph Neural Networks (S2GNNs). It visually compares the spatial message passing approach (MPGNNs) with the spectral filtering method. MPGNNs have a limited receptive field, constrained by the number of message passing steps, as shown by the cutoff in spatial distance and frequency. In contrast, S2GNNs utilize spectral filters, which allows for global information flow, shown as no cutoff, enabling them to overcome the limitations of MPGNNs. The figure highlights how S2GNNs combine spatial and spectral aspects synergistically, allowing for both local and global information propagation.

This figure demonstrates that spectral filters, unlike spatial message passing methods, do not suffer from over-squashing. Over-squashing is a phenomenon where information is lost when propagating through multiple layers of a graph neural network, especially when dealing with long-range dependencies. The figure shows that spectral filters maintain accuracy even at large distances between nodes. This is in contrast to the exponential decay in accuracy observed with spatial filters, which suggests that spatial methods are significantly limited in their capability to handle long-range interactions in graphs.
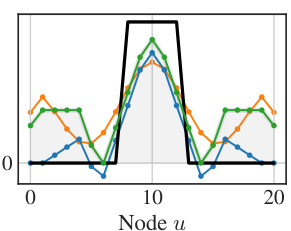
This figure compares the performance of three different types of filters in approximating a true filter with a discontinuity at λ = 0. The three types of filters are: S² filter (a synergistic combination of spatial and spectral filters), polynomial filter (Spa.), and spectral filter (Spec.). The figure shows that the S² filter perfectly approximates the true filter, while the polynomial and spectral filters alone do not. The figure also shows the responses of the three filters on a path graph, demonstrating that the S² filter is better at modeling long-range interactions.
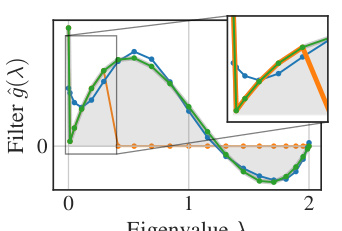
This figure shows a comparison of different filter approximations in the spectral and spatial domains. It demonstrates how the proposed Spatio-Spectral Graph Neural Network (S2GNN) filter effectively approximates a true filter with a discontinuity at λ = 0, which neither the polynomial filter nor the spectral filter alone can achieve. The graph in (b) further illustrates the superior performance of S2GNN in capturing long-range interactions on a path graph.
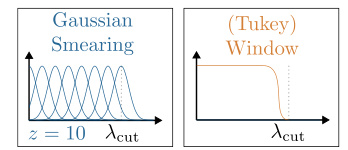
The figure shows the spectral filter function used in S2GNN. It’s composed of a linear combination of translated Gaussian basis functions, which is then multiplied by a Tukey window function that smoothly decays to zero around Acut. The Gaussian basis functions are used to smoothly approximate the filter across the eigenvalue spectrum, while the Tukey window function prevents overshooting near the frequency cutoff Acut. This combination leads to efficient and accurate approximation of the filter.

This figure shows the ringing effect that occurs when an ideal low-pass filter is used to approximate a discontinuous signal. The graph illustrates the overshooting that occurs near the discontinuity. The ‘window’ line in the legend represents the use of a smoothing window function to mitigate the ringing effect, while the ‘w/o’ line shows the overshooting that occurs without the smoothing window.
This figure illustrates the core principle of Spatio-Spectral Graph Neural Networks (S2GNNs). It shows how S2GNNs synergistically combine spatially and spectrally parametrized graph filters. The spatial message passing is limited to a certain distance cutoff (local), while the spectral filter operates globally. The combination of both overcomes the limitations of individual methods, leading to tighter approximation-theoretic error bounds. The figure also visually compares the spatial and spectral domains, highlighting the difference in their coverage (local vs. global).

The figure illustrates the main principle of Spatio-Spectral Graph Neural Networks (S2GNNs). It shows how S2GNNs synergistically combine spatial message passing with spectral filters, explicitly parametrized in the spectral domain. The left side depicts the spatial domain, showing how traditional message passing is limited to a local neighborhood. The right side illustrates the spectral domain, where the spectral filter is able to operate globally, capturing information from distant nodes that may be missed by traditional methods. The combination of spatial and spectral components in S2GNNs is highlighted as a key advantage, enabling both local and global information propagation.

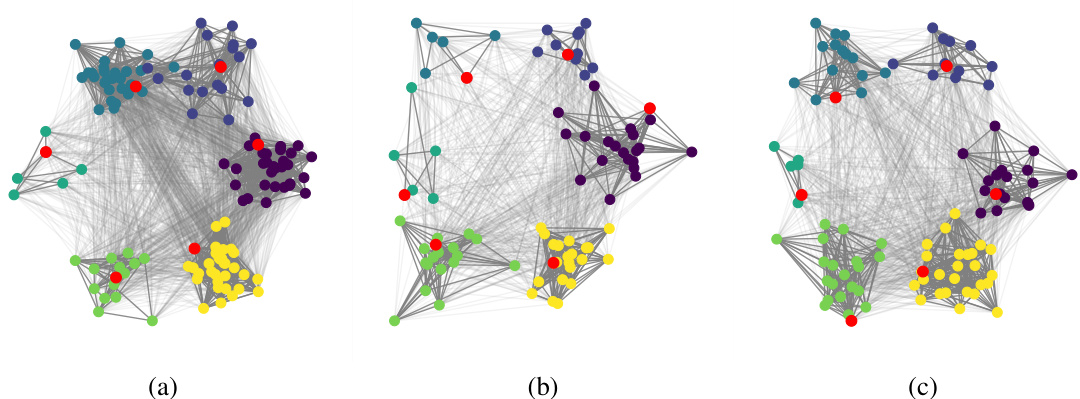
This figure visualizes four different spectral filters learned on the LR-CLUSTER dataset. The filters are represented as matrices where each cell’s color intensity corresponds to the filter’s value for the respective node pair. Yellow indicates a large positive value while blue shows a large negative value. White lines delineate clusters in the dataset, showing how the filters capture and differentiate between them. The figure demonstrates the way S2GNNs use spectral filters to capture both coarse and fine-grained cluster structures within the data.
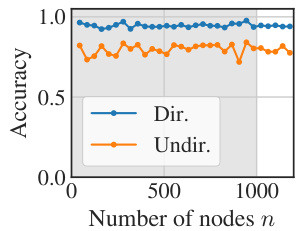
The figure shows the accuracy of S2GCN on the associative recall task. The accuracy is plotted against the number of nodes in the sequence. The graph shows that S2GCN achieves high accuracy even for very long sequences. The gray area represents the in-distribution data, while the other data points represent the out-of-distribution data.
This figure illustrates the core principle of Spatio-Spectral Graph Neural Networks (S²GNNs). It shows how S²GNNs combine spatial message passing (left) with spectral filtering (right) to achieve both local and global information propagation in graph neural networks. Spatial message passing is limited by a distance cutoff, while spectral filtering operates globally, capturing information from all parts of the graph. The combination of both approaches improves information propagation and reduces over-squashing, making S²GNNs more expressive and effective.

This figure shows the principle of Spatio-Spectral Graph Neural Networks (S2GNNs). It illustrates how S2GNNs synergistically combine spatial message passing (left side) with spectral filtering (right side). Spatial message passing operates locally, with information exchange limited by the number of hops. In contrast, spectral filtering operates globally, using information from the entire graph’s spectrum. The combination of these two approaches enables S2GNNs to capture both local and global dependencies in the graph data, thus overcoming the limitations of traditional MPGNNs which rely on just the spatial component.

This figure illustrates the core principle of Spatio-Spectral Graph Neural Networks (S2GNNs). It shows how S2GNNs synergistically combine spatially and spectrally parametrized graph filters. The left side depicts spatial message passing with a distance cutoff, while the right side illustrates spectral filtering operating globally, even on a truncated frequency spectrum. The combination of both approaches aims to overcome limitations of standard MPGNNs by enabling global yet efficient information propagation and alleviating over-squashing.

This figure illustrates the core principle of Spatio-Spectral Graph Neural Networks (S2GNNs). It shows how S2GNNs combine spatial message passing (local) with spectral filtering (global). The left side depicts a spatial message passing mechanism where information is propagated step-wise across the graph, limited by a distance cutoff. The right side depicts the spectral filtering mechanism, where a filter operates across the entire graph in the frequency domain, but efficiency considerations might require truncation of the frequency spectrum. The combination of these two approaches provides a synergistic benefit, overcoming limitations of traditional methods such as over-squashing.

This figure illustrates the main principle of Spatio-Spectral Graph Neural Networks (S2GNNs). It shows how S2GNNs synergistically combine spatially and spectrally parametrized graph filters. The spatial filter is limited to a local neighborhood (1-hop or l-hop), while the spectral filter operates globally on the entire graph or a truncated frequency spectrum. Combining both approaches effectively leverages their respective strengths for accurate long-range interactions.
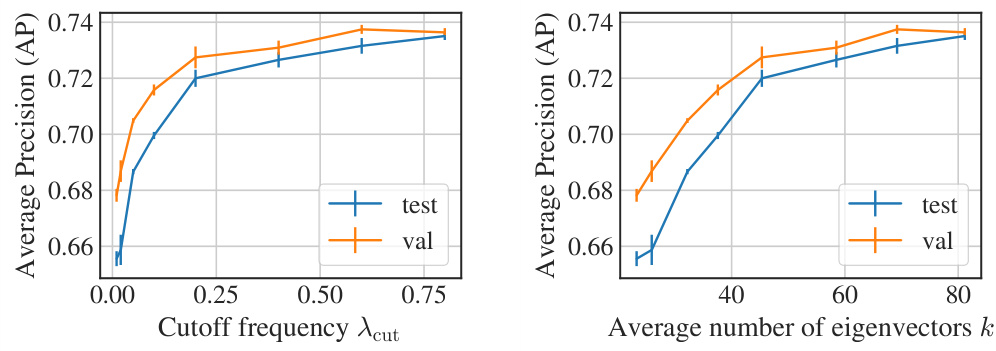
This figure shows the result of ablating the number of eigenvectors used in the spectral filter of S2GNN on the peptides-func dataset. The left panel shows the average precision (AP) plotted against the cutoff frequency (λcut), which indirectly controls the number of eigenvectors. The right panel shows the AP against the average number of eigenvectors (k). Both panels include separate lines showing results for validation and test sets. The results demonstrate the impact of the number of eigenvectors on the model’s performance, highlighting the benefit of including more eigenvectors for improved accuracy.

This figure illustrates the core principle of Spatio-Spectral Graph Neural Networks (S2GNNs). It highlights the synergistic combination of spatial message passing (local) and spectral filtering (global) within the GNN architecture. The left side showcases the limited receptive field of spatial message passing, confined to a certain distance cutoff. In contrast, the right side demonstrates how spectral filters provide access to the entire spectrum, enabling global information propagation despite potential frequency cutoffs. The comparison visually represents the strengths of both spatial and spectral approaches and how S2GNNs combine them for improved performance.
The figure shows the principle of Spatio-Spectral Graph Neural Networks (S2GNNs). It illustrates how S2GNNs synergistically combine spatially and spectrally parametrized graph filters to overcome the limitations of l-step MPGNNs, such as limited receptive field and over-squashing. It depicts a comparison between message passing (spatial) and spectral filtering methods in terms of locality, global reach, and frequency filtering capabilities.

This figure visualizes four different spectral filters learned on the LR-CLUSTER dataset. Each filter is represented as a matrix where the size of each entry corresponds to the filter’s weight for the specific interaction between nodes. The color indicates the sign of the weight (yellow for positive, blue for negative). White lines connect nodes belonging to the same cluster. The visualization shows how the spectral filters capture different aspects of the cluster structure, with some filters highlighting coarse-grained features while others identify finer-grained details within the clusters.
This figure illustrates the core principle of Spatio-Spectral Graph Neural Networks (S2GNNs). It visually explains how S2GNNs synergistically combine spatially and spectrally parameterized graph filters. The left side shows spatial message passing with a distance cutoff, while the right side depicts spectral filtering operating globally in the frequency domain. The combination of these two approaches addresses limitations of traditional message passing GNNs, such as limited receptive fields and information squashing.
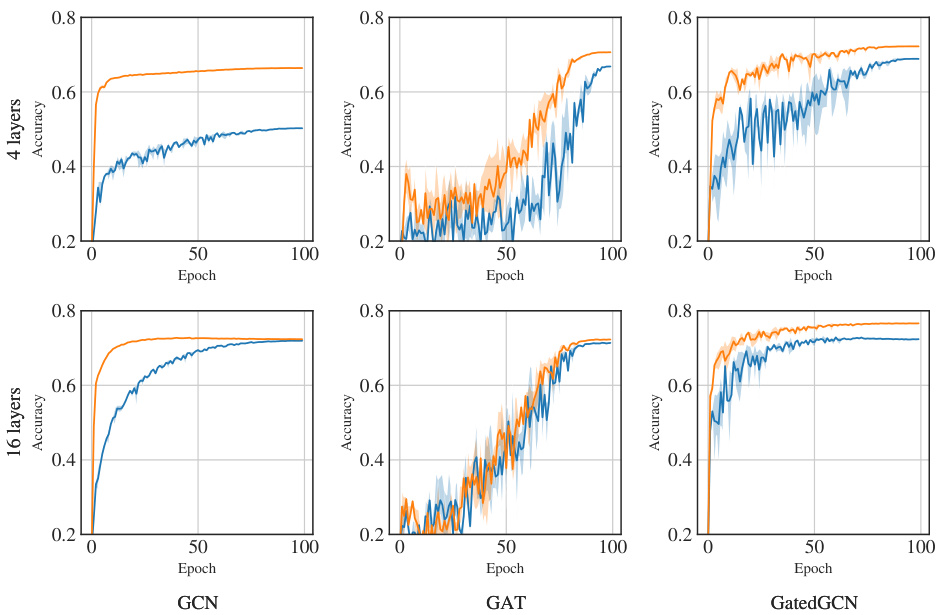
This figure presents the test accuracy curves for the SBM clustering task. It compares the performance of different models: MPGNN baselines and their corresponding S²GNN versions, with and without positional encodings. The curves show how the test accuracy changes over training epochs for each model, allowing for a visual comparison of their performance and convergence rates.
This figure illustrates the core principle of Spatio-Spectral Graph Neural Networks (S2GNNs). It shows how S2GNNs combine spatial message passing and spectral filtering to achieve efficient information propagation in graph neural networks. Specifically, it contrasts the limited receptive field of spatial message passing with the global reach of spectral filters. The combination of both methods enables S2GNNs to handle long-range interactions in graph data effectively.
This figure illustrates the core principle of Spatio-Spectral Graph Neural Networks (S2GNNs). It shows how S2GNNs combine spatial message passing with spectral filters to achieve efficient and expressive information propagation on graphs. The spatial message passing is limited to a certain number of hops (p=2, p=3), while the spectral filter operates globally across the entire graph, effectively handling long-range dependencies. The figure also visually compares the spatial and spectral filtering domains (spatial distance and frequency).

This figure illustrates the core principle of Spatio-Spectral Graph Neural Networks (S2GNNs). It shows how S2GNNs combine spatial message passing with spectral filters to model both local and global interactions within a graph. The left side depicts spatial message passing with a limited receptive field, while the right side shows spectral filtering, which operates globally in the frequency domain. The combination of spatial and spectral components enables S2GNNs to overcome the limitations of traditional message-passing models in handling long-range dependencies and over-squashing.
This figure illustrates the core principle of Spatio-Spectral Graph Neural Networks (S2GNNs). It shows how S2GNNs synergistically combine spatially and spectrally parametrized graph filters. Spatial message passing, represented on the left, is local and limited by a distance cutoff. Conversely, spectral filtering, shown on the right, operates globally, leveraging the strengths of both parametrizations to enable efficient and expressive information propagation across the entire graph. The key is to explicitly parametrize the spectral filter in the frequency domain, enabling global yet efficient information propagation.
More on tables

This table compares the performance of S2GNN with other state-of-the-art graph neural networks on two long-range interaction benchmark datasets: peptides-func and peptides-struct. The results show that S2GNN achieves state-of-the-art performance on peptides-func while using significantly fewer parameters than competing models. The table highlights the superior performance of S2GNN in modeling long-range interactions.

This table presents the results of applying GAT and S2GAT models on the OGB Products dataset. The table is split into three sections: Train, Val, and Test, reflecting the different stages of model training and evaluation. For each split and model, the accuracy and F1 score are reported. The S2GAT model consistently outperforms the GAT model across all three splits, indicating its effectiveness in improving performance on the OGB Products benchmark.

This table presents the results of graph ranking experiments on the TPUGraphs dataset using GCN and S2GCN models. The ’layout’ refers to a specific subset of the TPUGraphs data. The Kendall tau metric is used to evaluate the performance of the models. The table shows that S2GCN outperforms GCN on this task.

This table compares the performance of S2GNN with other state-of-the-art models on the peptides-func and peptides-struct datasets from the long-range benchmark. It shows that S2GNN achieves competitive performance while using significantly fewer parameters. The table highlights the superior performance of S2GNN, particularly with the addition of positional encodings.

This table compares the performance of S2GNN with other state-of-the-art graph neural networks on two long-range benchmark tasks: peptides-func and peptides-struct. It highlights that S2GNN achieves state-of-the-art performance on peptides-func while using significantly fewer parameters (approximately 35% less) than competing models. The table also provides the metrics used for evaluation (Average Precision for peptides-func and Mean Absolute Error for peptides-struct), indicating which models achieved the best and second-best results on each task.

This table compares the performance of S2GNN with other state-of-the-art models on two long-range interaction benchmark datasets: peptides-func and peptides-struct. The table shows that S2GNN achieves competitive performance with significantly fewer parameters.

This table presents statistics for various datasets used in the paper’s experiments, including the number of graphs, average number of nodes and edges, the type of task performed on each dataset (e.g., graph classification, node regression), and the license associated with each dataset. The datasets cover a range of sizes and complexities, reflecting the diversity of graph learning tasks.

This table shows the hyperparameters used in the experiments for each dataset. For each dataset, it shows the number of message passing layers, the number of spectral layers, the dimension of the node features, the number of spectral filters per layer, the number of eigenvectors used for the spectral filter, the spectral frequency cutoff, whether a neural network was used for the spectral filter, the training time, the time to compute the eigendecomposition, the GPU used for training, and any additional notes about the specific experiment setup. The training time and EVD time are given in hours and minutes.

This table presents the results of an ablation study on the peptides-func benchmark, focusing on different aggregation methods for combining spatial and spectral filters within the S2GNN model. It shows the test accuracy (AP) achieved using different aggregation functions (Concat, Sum, Mamba-like, Sequential) with and without normalization. The number of parameters for each model configuration is also included.
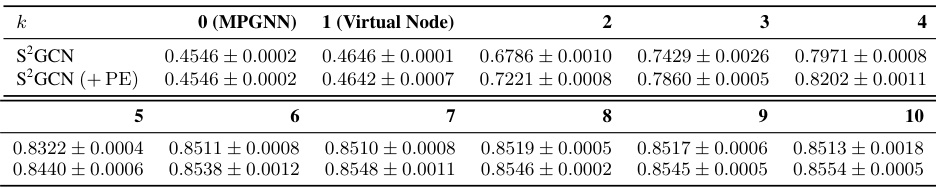
This table shows the accuracy results of the GMM clustering task using different numbers of eigenvectors (k). The experiment uses 4 Graph Convolutional Network (GCN) layers and one spectral layer at the end. The table compares the performance of S2GCN (with and without positional encodings) across different values of k, ranging from 2 to 10. It helps to understand the impact of spectral filter expressiveness on the GMM clustering task performance.

This table shows the accuracy results on the GMM clustering task for different numbers of message-passing (MP) layers. It compares the performance of a standard Graph Convolutional Network (GCN) model with the proposed Spatio-Spectral Graph Neural Network (S2GCN), which includes an additional spectral layer at the end. The table shows how the accuracy changes with different numbers of MP layers for both models, with and without positional encodings.

This table presents the results of the CLUSTER task from the Dwivedi et al. (2023) benchmark. It compares the performance of various GNN and transformer models on this node classification task. The table highlights the superior performance of the proposed S2GatedGCN model, showing it outperforms most GNN models and is competitive with several transformer-based approaches.

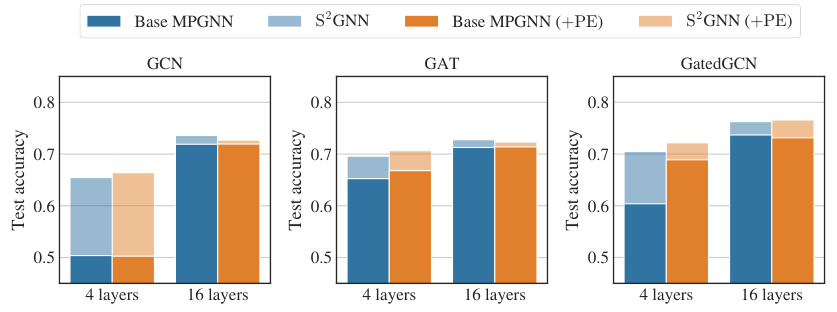
This table presents the ablation study on the SBM clustering task, comparing different configurations of MPGNN models (GCN, GAT, GatedGCN) with and without spectral filters and positional encodings. It shows the impact of these components on both training and test accuracy, highlighting the best performing configurations. The table includes columns for the MPGNN base model, the number of layers, inner dimension, the use of spectral filters, positional encodings, dropout rate, the number of parameters, training accuracy, and test accuracy.

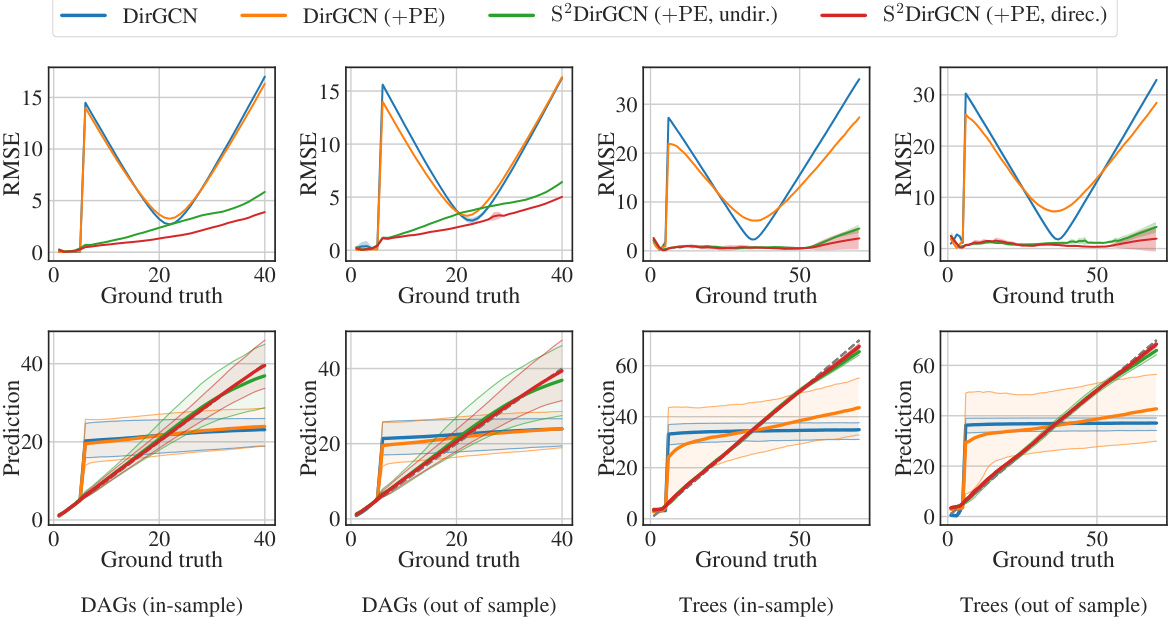
This table presents the results of the distance regression task. It compares the performance of several models, including a baseline DirGCN model and variants of S2DirGCN with and without positional encodings and directed/undirected spectral filters, on both in-distribution and out-of-distribution datasets. The evaluation metrics used are Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and R-squared (R²).

This table presents the results of the arXiv-year experiment, comparing the performance of different models on a large-scale heterophilic dataset. The best-performing model is shown in bold, and the second best is underlined. The results highlight the performance of the proposed S²DirGCN model in comparison to other state-of-the-art models.
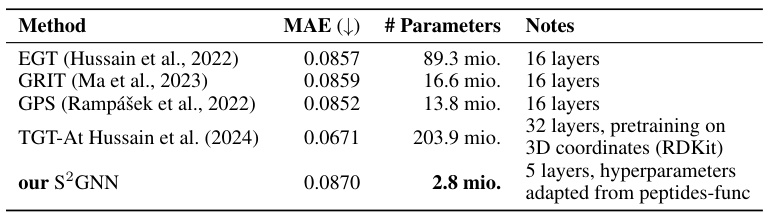
This table compares the performance of different models on the PCQM4Mv2 dataset. The Mean Absolute Error (MAE) and the number of parameters are reported for each model. The results show that the proposed S²GNN model achieves comparable performance to the state-of-the-art models while using significantly fewer parameters.
Full paper#



















