↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Reinforcement learning (RL) struggles with sample efficiency, especially in continuous state-action spaces where data is often scarce. Existing RL algorithms often exhibit slow convergence rates, hindering their applicability in various real-world scenarios. This paper addresses this challenge by providing a novel framework for analyzing RL in such continuous settings.
This new framework focuses on two key stability properties which ensure the “smooth” evolution of the system in response to policy changes. By establishing these properties, the authors prove that much faster convergence rates can be achieved. This is a significant breakthrough and it offers new perspectives on established RL optimization principles like pessimism and optimism, suggesting that fast convergence is possible even without explicitly incorporating these principles in the algorithms.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in reinforcement learning because it tackles the critical issue of sample efficiency in continuous state-action spaces, a notoriously challenging domain. The fast convergence rates achieved through novel stability analysis are highly significant and open up new avenues for developing more efficient RL algorithms. It challenges established dogma about the necessity of pessimism and optimism principles, suggesting potentially simpler and more efficient approaches. The proposed framework and its results are broadly applicable beyond specific algorithms, advancing theoretical understanding and practical applications of RL.
Visual Insights#
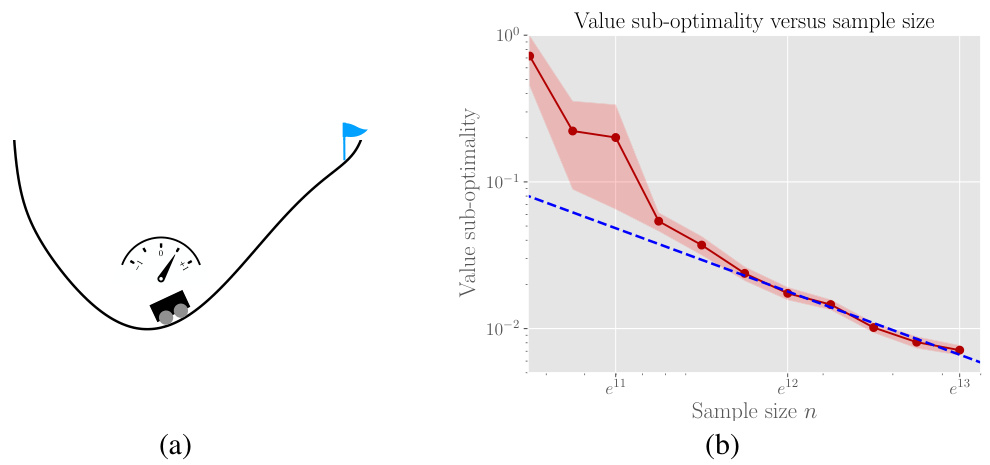
The figure shows an illustration of the fast rate phenomenon observed in the Mountain Car problem using Fitted Q-Iteration (FQI). The left panel (a) shows a schematic of the Mountain Car environment. The right panel (b) plots the value sub-optimality against the sample size (n). Each red point represents the average value sub-optimality over 80 Monte Carlo trials, with the shaded area indicating twice the standard error. A linear least-squares fit to the last 6 data points is also shown (blue dashed line) to highlight the convergence rate of approximately -1, much faster than the typical -0.5 convergence rate.
Full paper#



















