↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Ensembling deep neural networks enhances model generalization, but scaling ensemble methods for large models is computationally expensive. Existing methods, such as those based on Bayesian approaches or sampling techniques, often require significant computational resources. Low precision in representing model parameters is common for resource efficiency, but is often seen as a limitation, rather than an opportunity.
This paper introduces a novel method called Low Precision Ensembling (LPE) that addresses these limitations. LPE uses a training-free ensemble construction method leveraging low-precision number systems with Bernoulli Stochastic Rounding. The core idea is that the quantization errors inherent in low-precision systems can be viewed as a source of diversity among ensemble members. Experiments demonstrate that LPE is effective, competitive with Bayesian approaches, memory-efficient, and scalable for large models, thereby demonstrating the feasibility and value of this approach.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel and efficient approach to ensembling large models, addressing the scalability challenges associated with existing methods. It leverages the inherent diversity introduced by low-precision number systems to improve model performance without any further training, offering a valuable solution for resource-constrained settings and pushing the boundaries of ensemble techniques in the age of large-scale models. The findings are particularly significant for researchers working with resource-intensive models or those focused on enhancing the robustness of deep learning systems. The method’s simplicity and effectiveness open up new avenues for further research in low-precision computing and Bayesian deep learning.
Visual Insights#
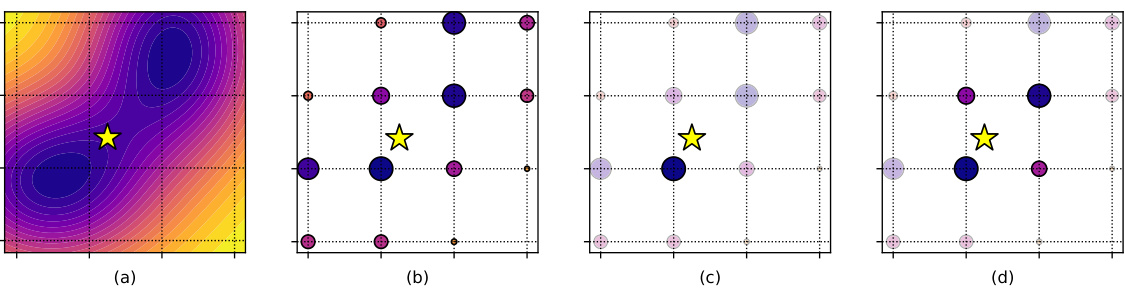
This figure illustrates the concept of low-precision ensembling. Panel (a) shows a loss landscape with a pre-trained model (yellow star). Panel (b) shows how quantization creates a discrete set of possible weights. Panel (c) demonstrates that traditional quantization selects the closest weight. Finally, Panel (d) highlights that low-precision ensembling leverages many high-performing models near the optimal weight, leading to improved performance.
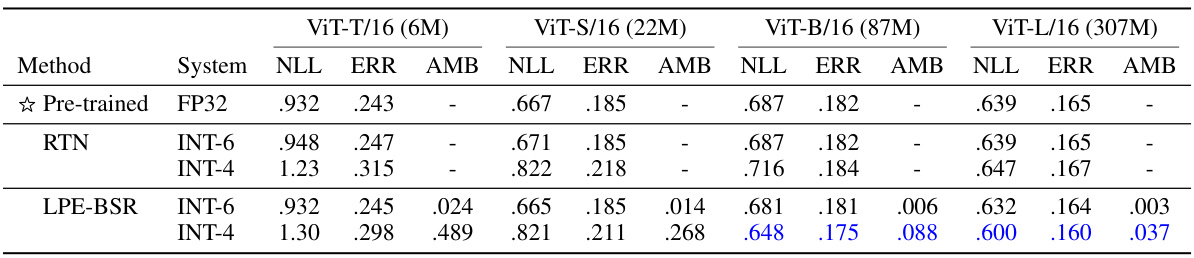
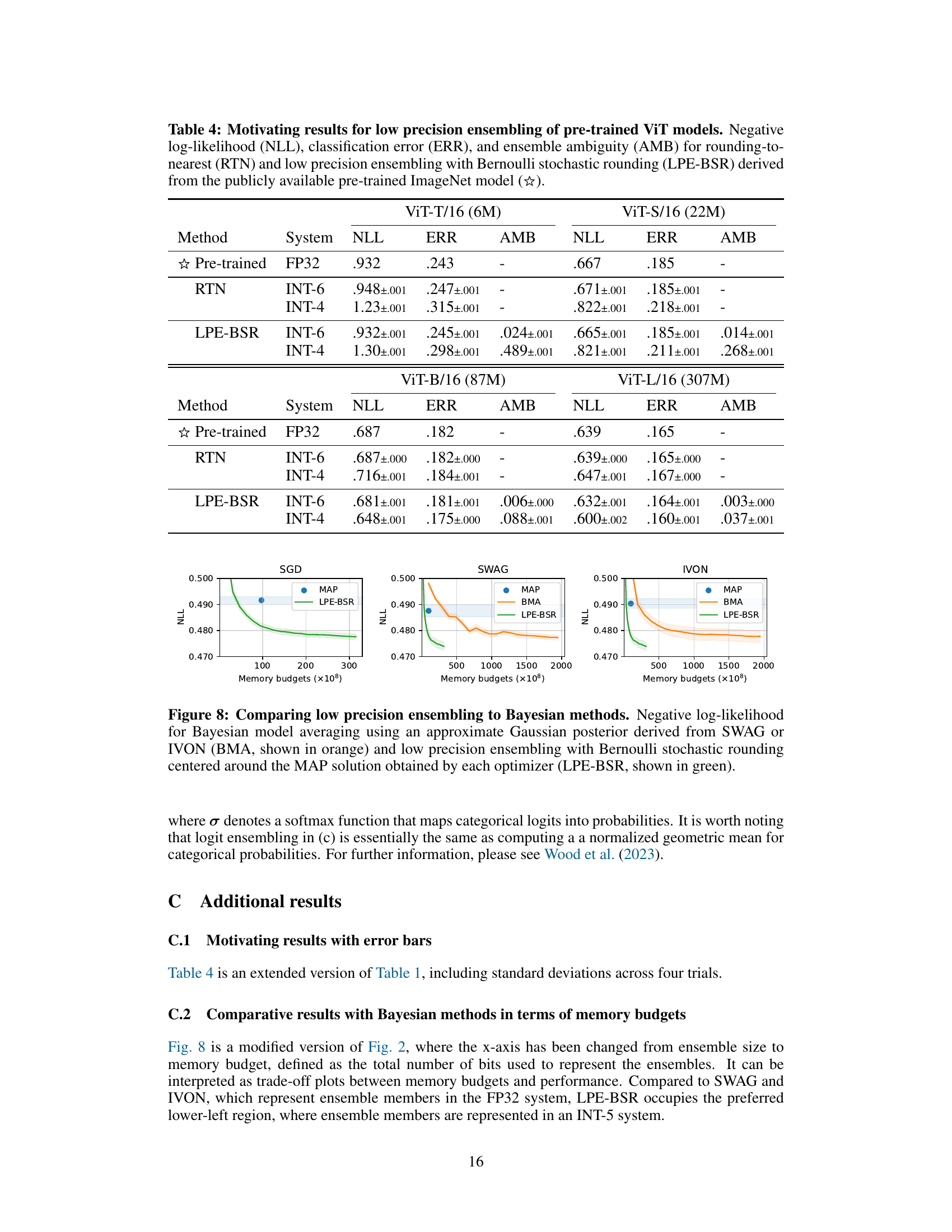
This table presents the results of experiments using pre-trained Vision Transformer (ViT) models. It compares the performance of two methods: rounding-to-nearest (RTN) and the proposed low precision ensembling with Bernoulli stochastic rounding (LPE-BSR). The table shows negative log-likelihood (NLL), classification error (ERR), and ensemble ambiguity (AMB) for different ViT model sizes (ViT-T/16, ViT-S/16, ViT-B/16, ViT-L/16) and different integer precision levels (INT-6, INT-4). The results highlight the superior performance of LPE-BSR, especially for larger models and lower precision settings.
In-depth insights#
Low Precision Ensembling#
Low precision ensembling is a novel technique that leverages the quantization errors inherent in low-precision number systems to enhance the diversity of ensemble members. Instead of viewing these errors as flaws, the method uses them to generate multiple, distinct models from a single pre-trained model, improving overall performance without additional training. This approach proves particularly beneficial for large models where traditional ensembling methods are limited by their computational cost and memory requirements. Empirical results show that low precision ensembling successfully creates diverse ensemble members that improve downstream performance, surpassing traditional techniques in both accuracy and efficiency. The training-free nature of the method is a significant advantage, making it easily adaptable to real-world applications with limited computational resources. While initial experiments focused on simpler, symmetric quantization, further exploration of more sophisticated rounding schemes could unlock even greater potential. This approach offers a scalable and cost-effective solution for building diverse ensembles of large models in the era of large-scale deep learning.
LPE-BSR Method#
The Low Precision Ensembling with Bernoulli Stochastic Rounding (LPE-BSR) method offers a novel approach to ensemble creation by leveraging the inherent quantization errors introduced when using low-precision number systems. Instead of treating these errors as flaws, LPE-BSR uses them to generate ensemble diversity. The method is particularly advantageous for large models, where the memory cost of traditional ensemble methods can be prohibitive. LPE-BSR is training-free, requiring only a single, pre-trained model as input. Its simplicity and efficiency make it a promising solution for improving the generalization performance of large models in resource-constrained environments. By randomly rounding weights to the nearest representable value in a low-precision system, LPE-BSR effectively explores the neighborhood of the original high-precision weights, sampling multiple high-performing models from a single basin. The method’s effectiveness stems from its ability to generate diverse ensemble members, without the need for extensive computational resources associated with techniques like Bayesian model averaging.
Bayesian Ensemble#
Bayesian ensembles offer a powerful approach to improve model robustness and predictive performance by combining multiple models. The core idea is to treat model parameters as random variables and to approximate the posterior distribution over these parameters. This contrasts with traditional ensembling methods that merely aggregate predictions. Bayesian approaches provide a principled way to quantify uncertainty and model diversity, leveraging techniques like stochastic weight averaging (SWAG) or improved variational online Newton (IVON) to estimate the posterior. The resulting ensemble benefits from the diverse perspectives of individual members, improving generalization, particularly in challenging scenarios with high uncertainty. A critical aspect of Bayesian ensembling is the efficiency of posterior approximation: computationally expensive methods may limit scalability for very large models. Low precision techniques offer a promising direction towards addressing computational limitations, enabling construction of diverse ensembles while reducing memory footprints. The trade-off between diversity, accuracy, and computational efficiency remains a key challenge in the development and application of efficient Bayesian ensemble methods.
Diversity and Accuracy#
The interplay between diversity and accuracy in ensemble methods is a crucial aspect of machine learning. Diversity refers to the extent to which individual models in an ensemble make different predictions; higher diversity generally leads to better generalization. Accuracy, on the other hand, represents the individual model’s predictive performance. Ideally, one seeks an ensemble with high accuracy and high diversity, as highly accurate yet similar models offer limited improvement. The challenge lies in balancing these two factors. Methods focusing solely on diversity may inadvertently include low-accuracy models, negatively impacting the overall ensemble performance. Conversely, overly prioritizing accuracy can lead to ensembles lacking sufficient diversity, reducing the potential benefits. Strategies for achieving optimal diversity and accuracy involve careful model selection, training procedures (such as using different initializations or data subsets), and post-processing techniques, demonstrating that finding the right balance is essential for building robust and effective ensembles.
Future Work#
Future research directions stemming from this low-precision ensembling work could explore more sophisticated quantization methods beyond uniform quantization, potentially leading to even greater diversity and improved performance. Investigating the impact of different rounding techniques and exploring non-uniform quantization schemes is crucial. Furthermore, a comprehensive evaluation on diverse hardware platforms is needed to assess the practical latency gains achievable with low-precision ensembling. Extending this approach to other model architectures beyond vision transformers and language models would demonstrate broader applicability and highlight the method’s generality. Finally, exploring the interplay between low-precision ensembling and other advanced ensemble techniques, like Bayesian optimization or model distillation, offers exciting possibilities for further performance improvements and the development of novel, highly efficient and scalable ensemble methods.
More visual insights#
More on figures

The figure compares the performance of low precision ensembling (LPE-BSR) with Bayesian model averaging (BMA) using SWAG or IVON. It shows negative log-likelihood (NLL) plotted against ensemble size for three different optimization methods (SGD, SWAG, IVON). LPE-BSR consistently achieves comparable or better performance than BMA, demonstrating the effectiveness of the proposed low-precision method.

This figure compares the performance of the proposed Low Precision Ensembling with Bernoulli Stochastic Rounding (LPE-BSR) method to two Bayesian methods: Improved Variational Online Newton (IVON) and Stochastic Weight Averaging Gaussian (SWAG). The plots show the negative log-likelihood (NLL) for Bayesian model averaging (BMA) using IVON or SWAG and LPE-BSR. The results demonstrate that LPE-BSR, despite working within the constraints of a discrete low-precision space, achieves comparable performance to the Bayesian methods, which have access to the full continuous weight space. This suggests LPE-BSR can effectively leverage quantization errors to enhance ensemble diversity.
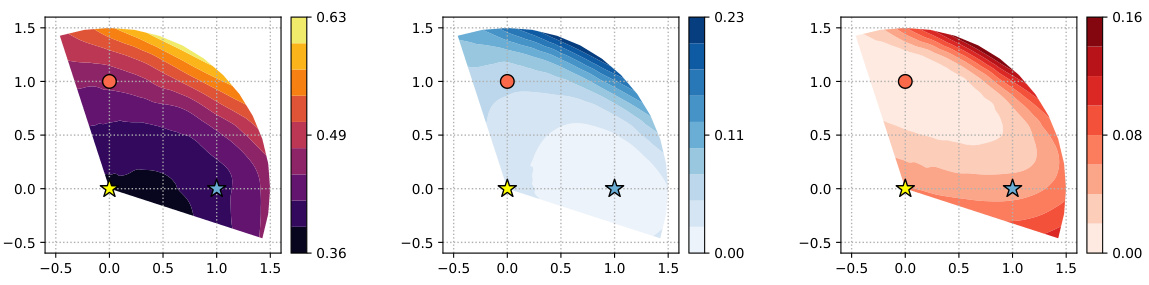
This figure shows a comparison of snapshot ensemble and low precision ensemble methods. It uses radial landscape plots to visualize a two-dimensional subspace of the model’s weight space. Three points are highlighted: the first and second snapshot samples from stochastic gradient Langevin dynamics (SSE), and a sample from low precision ensembling with Bernoulli stochastic rounding (LPE-BSR). The plots illustrate the negative log-likelihood (loss), and differences between the samples to show their diversity and location on the loss landscape. LPE-BSR produces a sample distinct from the SSE snapshots, suggesting that LPE-BSR can contribute diverse models to an ensemble even when starting from the same model.
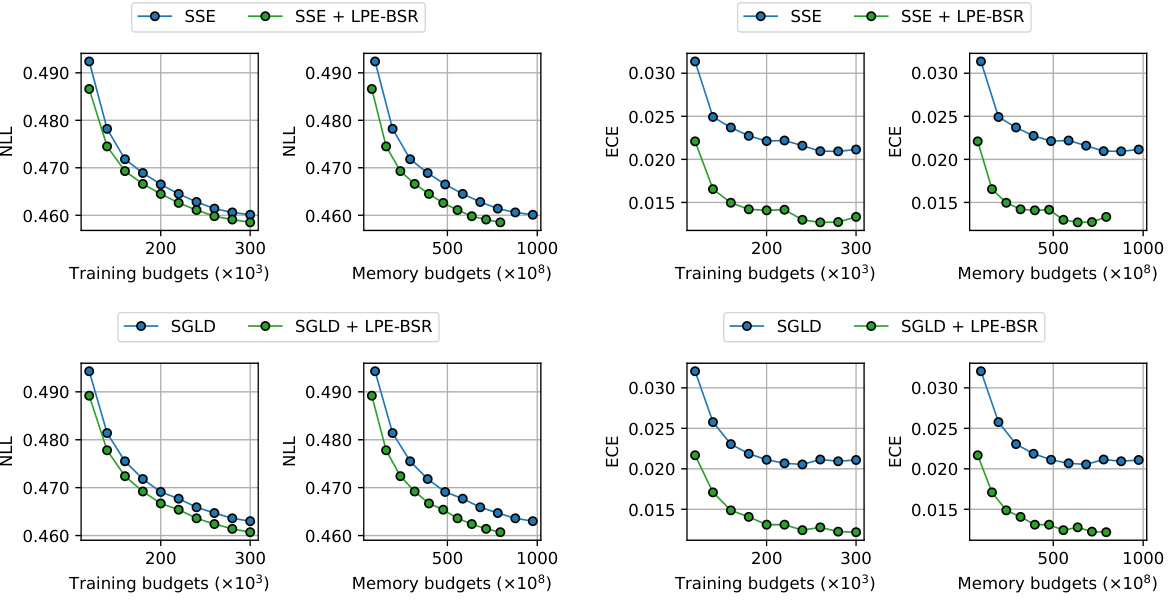
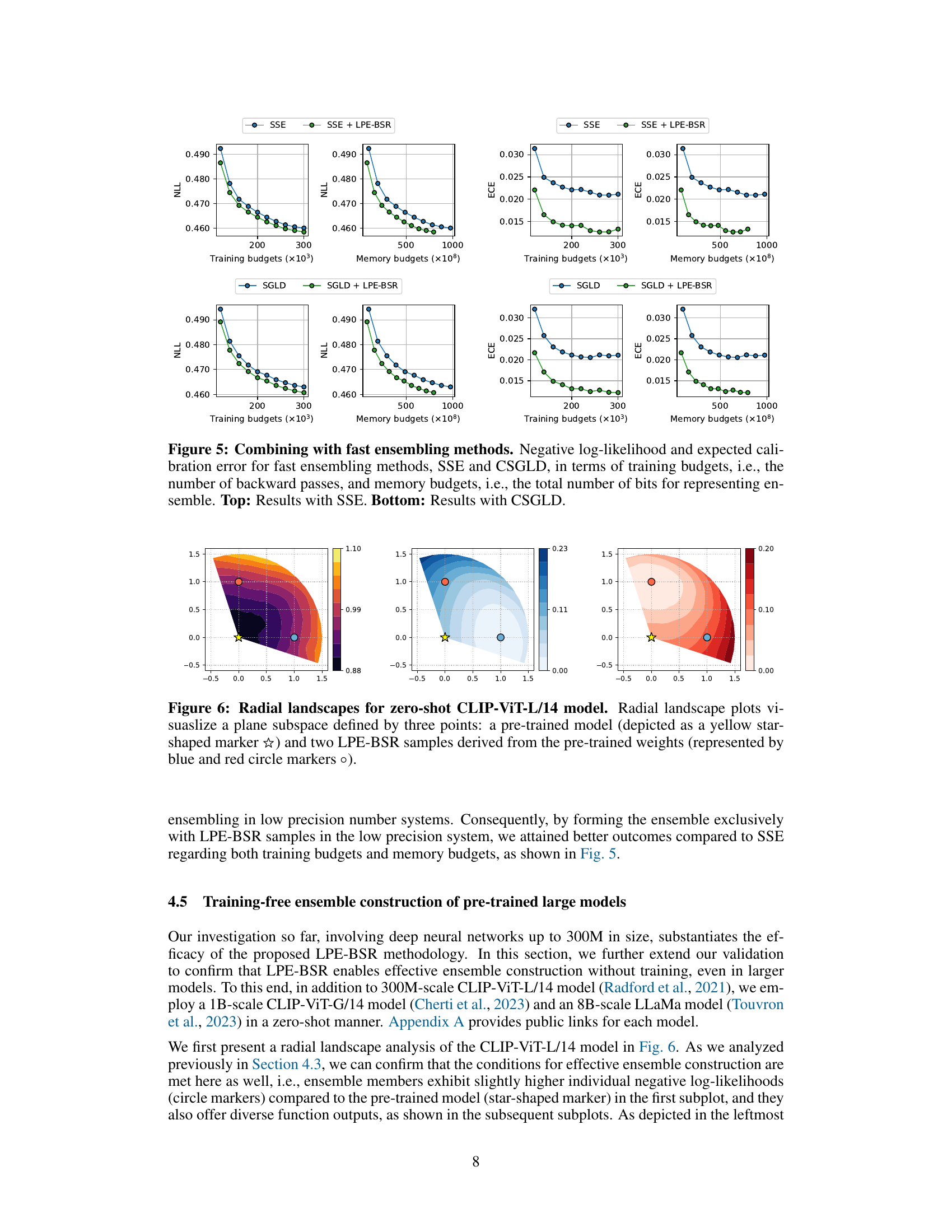
This figure compares the performance of two fast ensembling methods (SSE and CSGLD) with and without the addition of LPE-BSR. The results are shown in terms of both training budgets (number of backward passes) and memory budgets (total number of bits to represent the ensemble). The top row displays results using SSE, while the bottom row shows results using CSGLD. The graphs illustrate how the addition of LPE-BSR impacts both negative log-likelihood (NLL) and expected calibration error (ECE) for various training and memory budget levels.

This figure compares the performance of three different methods: IVON (Improved Variational Online Newton), BMA (Bayesian Model Averaging), and LPE-BSR (Low Precision Ensembling with Bernoulli Stochastic Rounding). It uses radial landscape plots to visualize a 2D subspace of the model’s weight space. The plots show how samples generated by each method are distributed around the MAP (Maximum A Posteriori) solution found by IVON. The purpose is to illustrate that LPE-BSR, despite working within a low-precision number system, is able to identify diverse ensemble members comparable to those produced by more computationally intensive Bayesian methods.

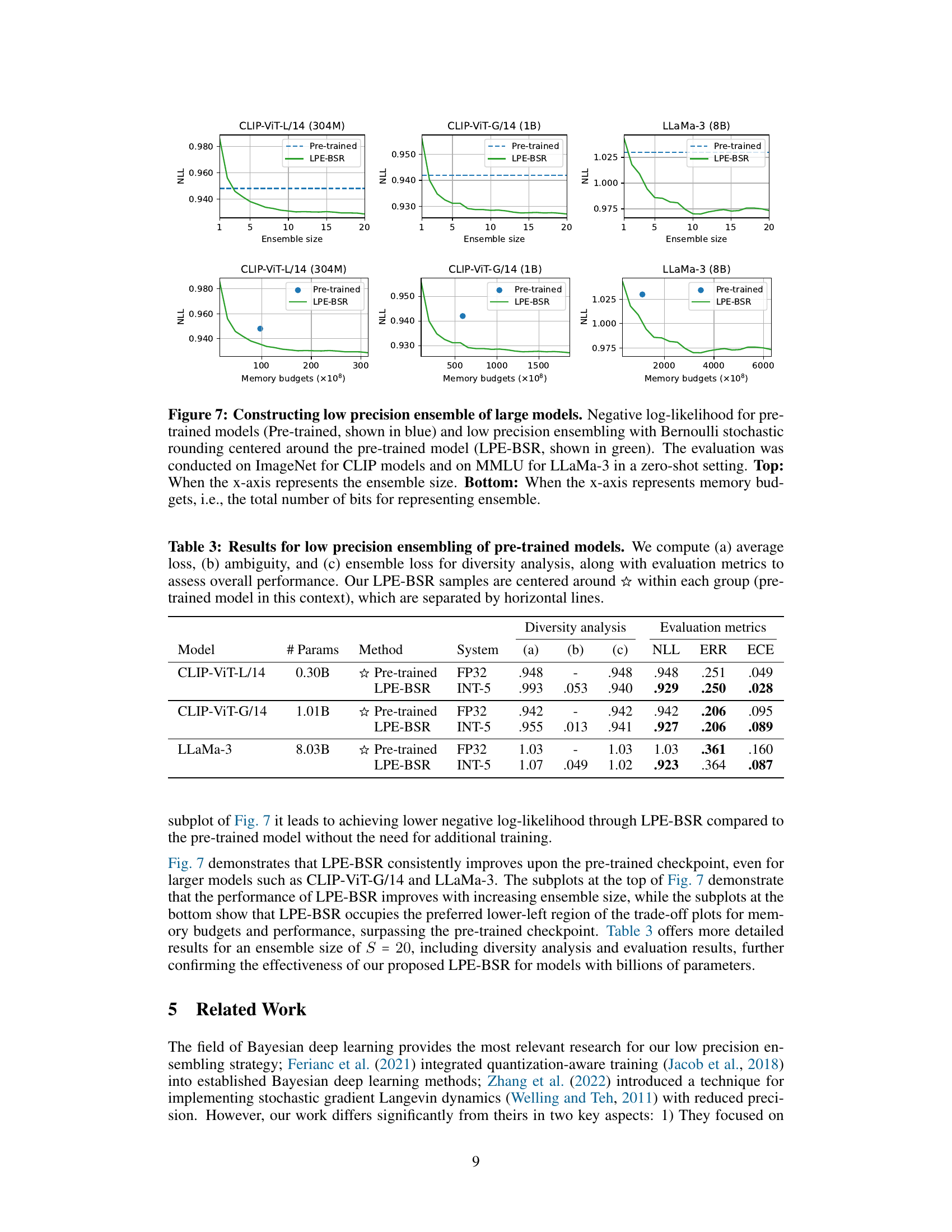
This figure shows the results of constructing low precision ensembles of three large models: CLIP-ViT-L/14 (304M), CLIP-ViT-G/14 (1B), and LLaMa-3 (8B). The top row displays the negative log-likelihood (NLL) as a function of ensemble size for both pre-trained models and those created using the low-precision ensembling with Bernoulli stochastic rounding (LPE-BSR) method. The bottom row shows the same data, but this time plotted against memory budget (total bits used to represent the ensemble). The results demonstrate that LPE-BSR consistently improves upon the performance of pre-trained models, particularly as the size of the models increases.
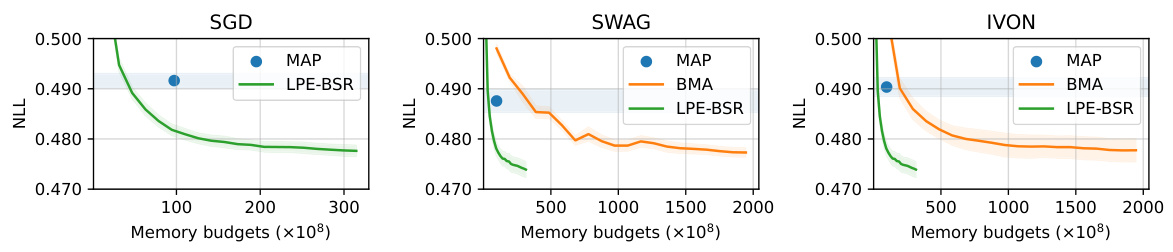
This figure compares the performance of low precision ensembling (LPE-BSR) with Bayesian model averaging (BMA) using SWAG or IVON methods. It shows the negative log-likelihood for each method as a function of memory budget. The LPE-BSR method is shown to be competitive with the Bayesian methods, especially when using SGD optimizer, indicating the effectiveness of LPE-BSR in achieving low memory and high accuracy.
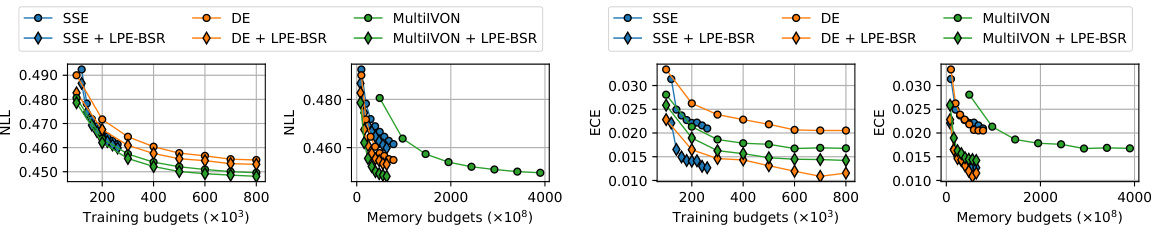
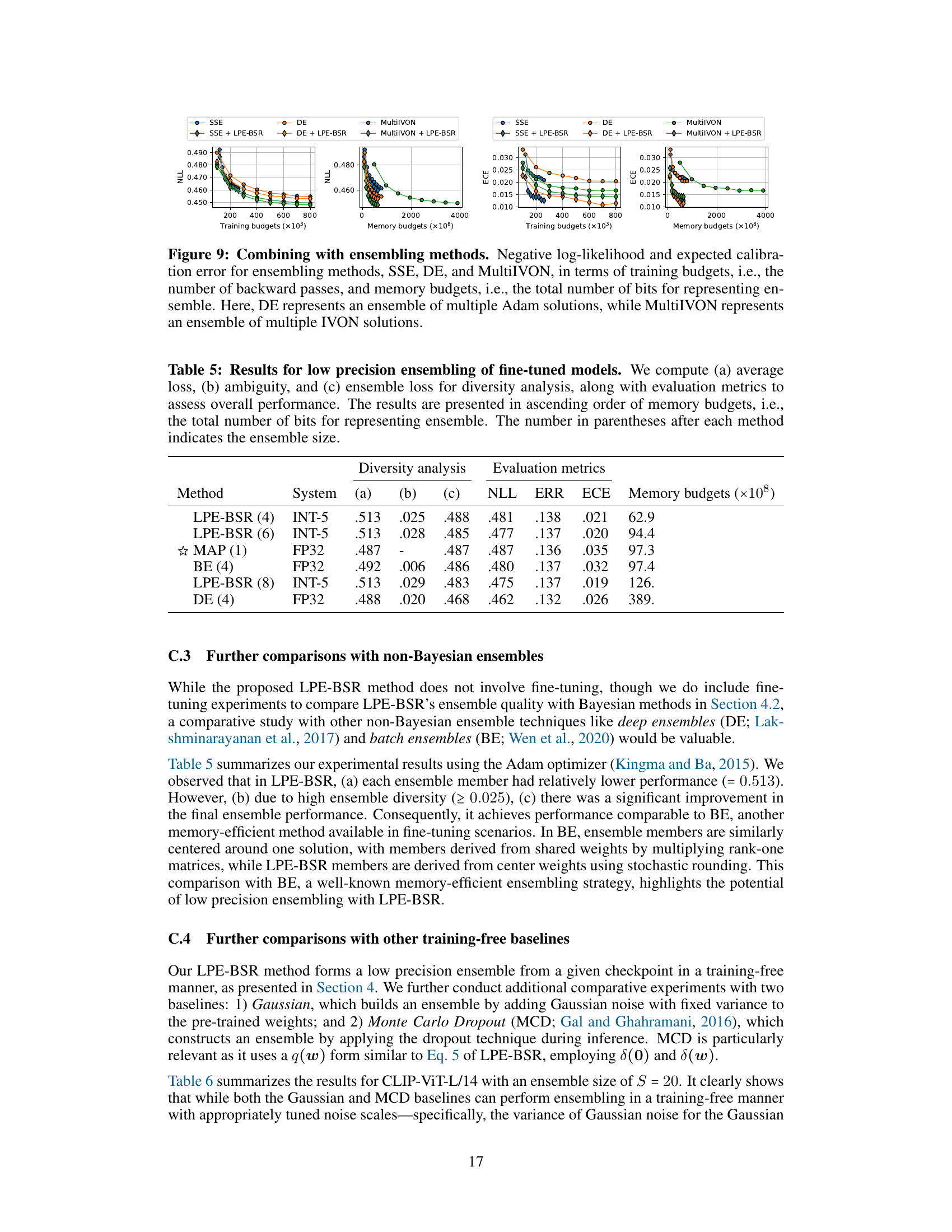
This figure compares the performance of several ensembling methods (SSE, DE, MultiIVON) with and without the addition of low-precision ensembling (LPE-BSR). It shows negative log-likelihood (NLL) and expected calibration error (ECE) as functions of both training budgets (number of backward passes) and memory budgets (total number of bits used for the ensemble). The results illustrate the impact of incorporating LPE-BSR on the efficiency and performance of the different ensembling techniques. The plots demonstrate that combining methods often improves the performance compared to using only one of the methods, even with increased memory cost.
More on tables
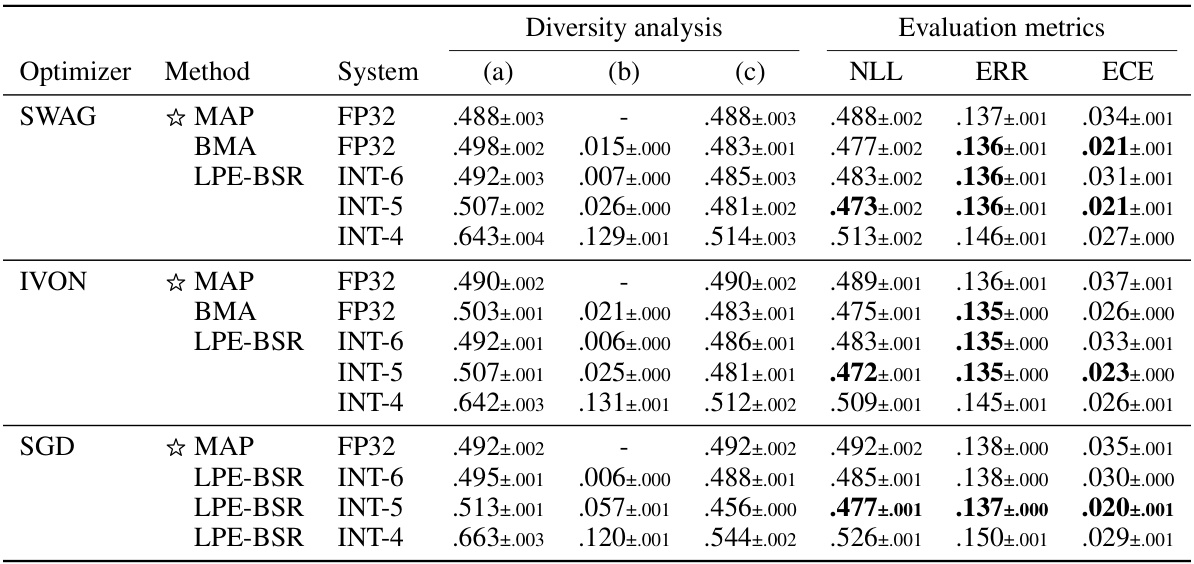
This table presents the results of experiments on pre-trained Vision Transformer (ViT) models, comparing the performance of rounding-to-nearest (RTN) quantization with the proposed Low Precision Ensembling with Bernoulli Stochastic Rounding (LPE-BSR) method. The table shows negative log-likelihood (NLL), classification error (ERR), and ensemble ambiguity (AMB) for different model sizes (ViT-T/16, ViT-S/16, ViT-B/16, ViT-L/16) and integer quantization bit depths (INT-6, INT-4). The results demonstrate the superiority of LPE-BSR, especially for larger models and lower precision settings, highlighting its ability to maintain and improve performance despite the use of low-precision representations.
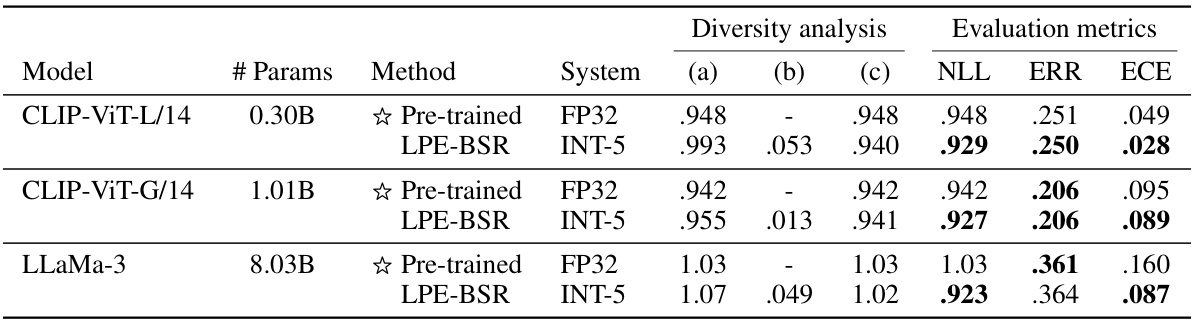
This table presents a comparison of the performance of different methods for low-precision ensembling of pre-trained models. It shows the average loss, ambiguity, ensemble loss, negative log-likelihood (NLL), classification error (ERR), and expected calibration error (ECE) for each method. The methods compared include the pre-trained models and the proposed LPE-BSR method, with results presented for different precision levels (INT-5). The table also indicates the ensemble size used for each method.
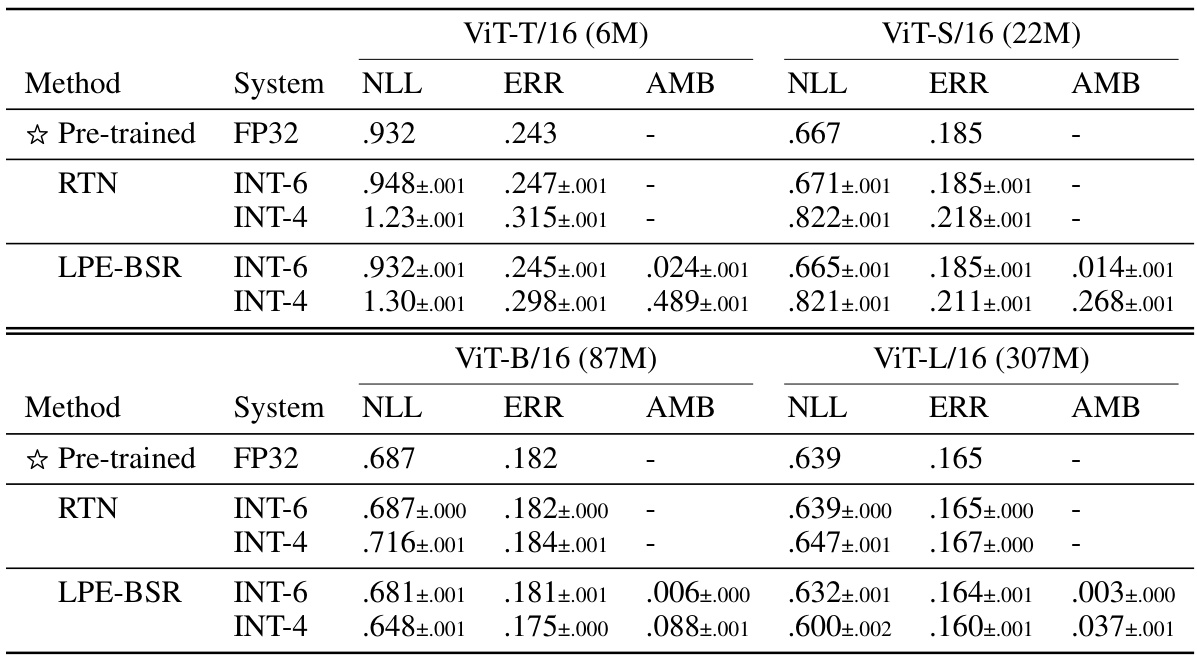
This table presents the results of experiments evaluating the performance of low precision ensembling on pre-trained Vision Transformer (ViT) models. It compares two methods: rounding-to-nearest (RTN) and the proposed low precision ensembling with Bernoulli stochastic rounding (LPE-BSR). The table shows negative log-likelihood (NLL), classification error (ERR), and ensemble ambiguity (AMB) for different ViT model sizes (ViT-T/16, ViT-S/16, ViT-B/16, ViT-L/16) and different integer quantization levels (INT-6, INT-4). The results demonstrate the effectiveness of LPE-BSR, especially for larger models and lower precision settings.
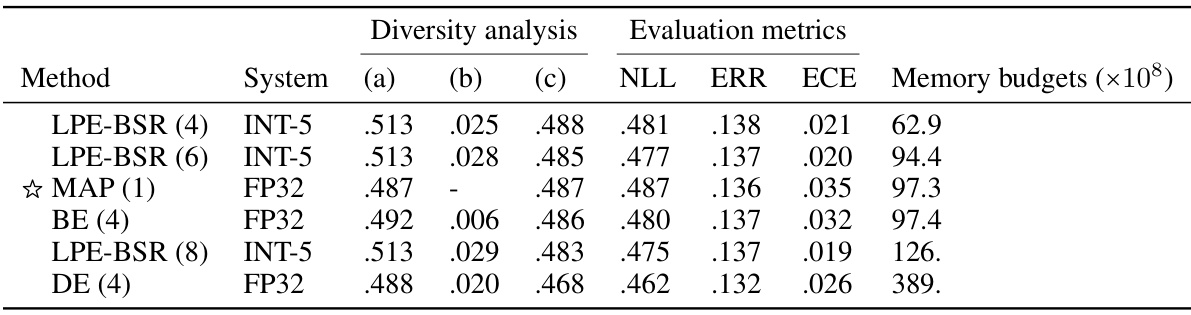
This table compares different ensembling methods (LPE-BSR with different ensemble sizes, MAP, BE, and DE) in terms of their performance on a fine-tuned model. It shows average loss, ambiguity (a measure of diversity), ensemble loss, negative log-likelihood (NLL), error rate (ERR), expected calibration error (ECE), and memory budget (total bits used for the ensemble). The results highlight the trade-off between ensemble diversity and performance, showing how LPE-BSR achieves competitive performance while using less memory compared to other methods.

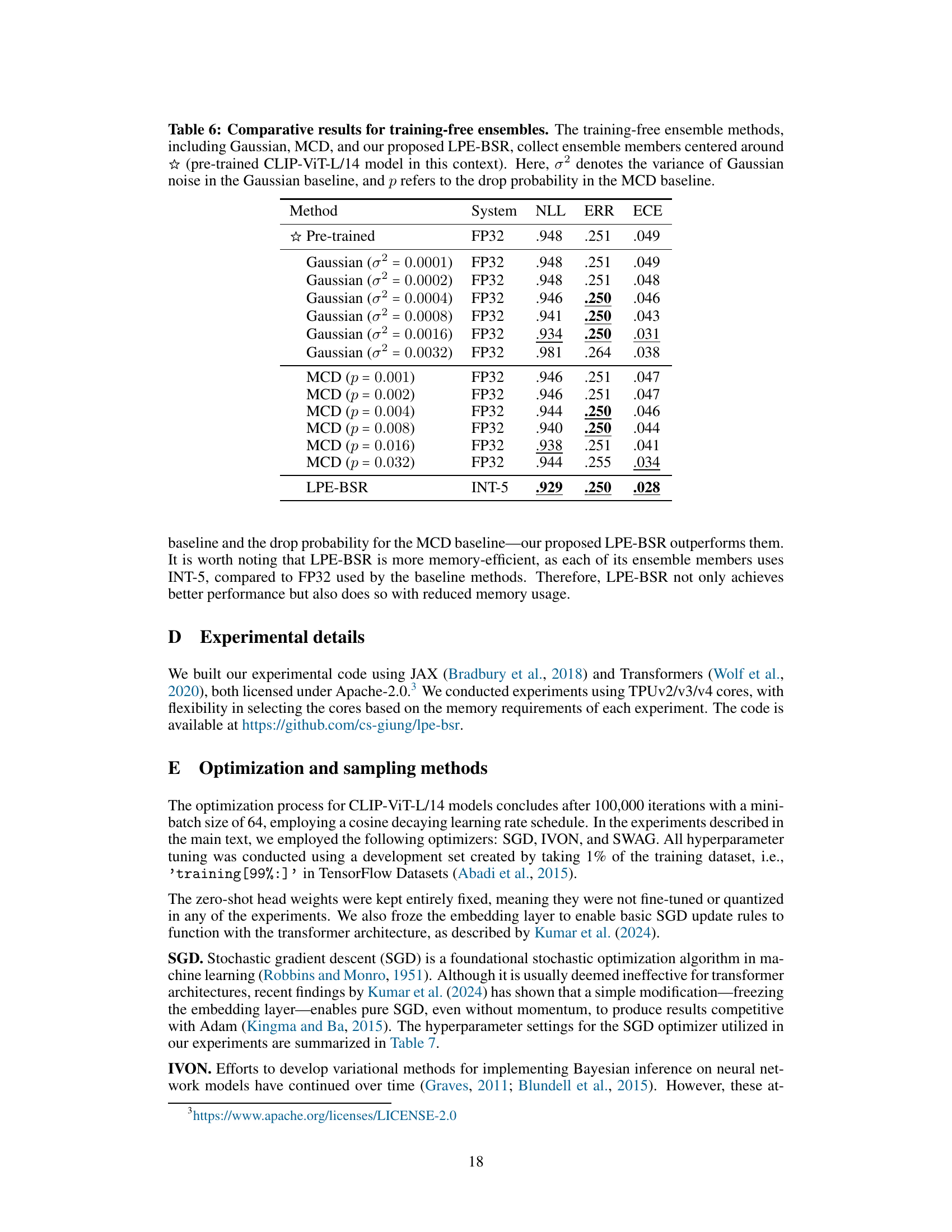
This table compares the performance of three training-free ensemble methods: Gaussian, Monte Carlo Dropout (MCD), and the proposed Low Precision Ensembling with Bernoulli Stochastic Rounding (LPE-BSR). It shows the negative log-likelihood (NLL), classification error (ERR), and expected calibration error (ECE) for each method on the CLIP-ViT-L/14 model. The results demonstrate that LPE-BSR achieves superior performance compared to the Gaussian and MCD baselines, while also being more memory-efficient.
This table presents the results of experiments evaluating the performance of low-precision ensembling (LPE-BSR) compared to rounding-to-nearest (RTN) on various sizes of pre-trained Vision Transformer (ViT) models. The metrics used are Negative Log-Likelihood (NLL), classification error (ERR), and ensemble ambiguity (AMB). The table shows that LPE-BSR often outperforms RTN, particularly in larger models and lower precision settings. The star symbol (☆) represents the pre-trained model in FP32.
Full paper#