↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Signed Graph Neural Networks (SGNNs) struggle with real-world data limitations, specifically sparse graphs and imbalanced triangle structures. These issues hinder accurate prediction of relationships within signed networks, a common task in social network analysis. Existing data augmentation methods aren’t directly applicable to SGNNs due to the lack of side information.
To tackle this, the authors propose a novel framework called Signed Graph Augmentation (SGA). SGA first detects potential edges by analyzing network structure using SGNNs, then selects the most beneficial edges to avoid adding more unbalanced triangles. Finally, SGA incorporates edge difficulty scores to enhance the training process. Extensive experimental results demonstrate that SGA significantly boosts the performance of various SGNN models, achieving improvements of up to 26.2% in F1-micro across six real-world datasets. The framework also provides a theoretical generalization error bound that proves the limitations of simple DropEdge methods.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses persistent challenges in Signed Graph Neural Networks (SGNNs): graph sparsity and unbalanced triangles. It offers a novel data augmentation method (SGA), improving SGNN performance and providing a theoretical error bound analysis, significantly advancing the field. This opens new avenues for research into more effective SGNN training techniques and broader understanding of their limitations.
Visual Insights#
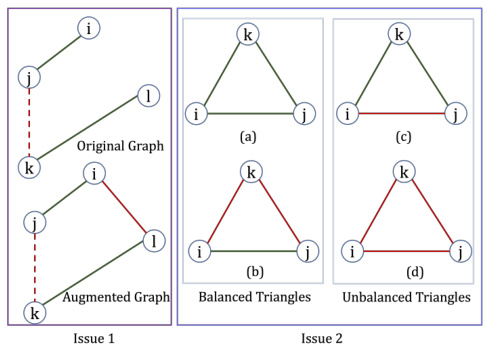
This figure illustrates two issues in Signed Graph Neural Networks (SGNNs). Issue 1 shows the challenge of predicting the edge sign between two nodes in a sparse graph, which is mitigated by adding extra edges through data augmentation. Issue 2 depicts the problem of unbalanced triangles, where the relationship between two nodes is uncertain, leading to difficulty in learning representations for these nodes. The figure uses green and red lines to represent positive and negative edges, respectively; solid lines indicate edges in the training set, while dashed lines show test set edges.

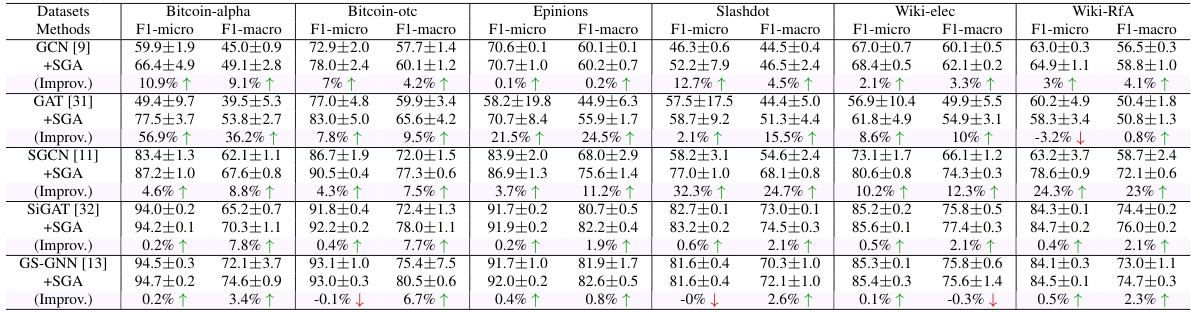
This table presents the results of link sign prediction experiments conducted on six real-world benchmark datasets. The results are shown for five different graph neural network (GNN) models: GCN, GAT, SGCN, SiGAT, and GS-GNN. For each model, the table shows the Area Under the Curve (AUC) and F1-binary scores, along with their standard deviations. It also indicates the improvement achieved by incorporating the proposed Signed Graph Augmentation (SGA) framework.
In-depth insights#
SGNN Augmentation#
The concept of “SGNN Augmentation” revolves around enhancing Signed Graph Neural Networks (SGNNs) by incorporating data augmentation techniques. SGNNs, designed for signed graphs (edges with positive or negative signs), often struggle with sparsity and imbalanced triangles. Data augmentation aims to address these limitations by generating new, synthetic training data that expands the graph’s structure and balances the class distribution of edge signs. This approach can involve adding or removing edges, altering edge signs, or introducing new nodes based on learned network features. The effectiveness hinges on carefully selecting augmentations that reduce the impact of inherent structural biases and avoid introducing spurious correlations. A successful augmentation strategy needs to consider the properties of signed graphs, the specific SGNN architecture used, and the downstream task (e.g., link sign prediction). While random edge manipulation can be ineffective, methods that leverage network structure or balance theory to guide augmentation may lead to significant performance improvements. Ultimately, this involves a tradeoff between creating diverse training samples and preserving the inherent characteristics of signed graphs.
SGA Framework#
The Signed Graph Augmentation (SGA) framework presents a novel approach to enhance Signed Graph Neural Networks (SGNNs) performance. Addressing the limitations of existing SGNNs, particularly sparsity and imbalanced triangles in real-world signed graph datasets, SGA leverages a multi-stage process. Firstly, it generates candidate edges using a pre-trained SGNN as an encoder to learn node embeddings, creating potential positive and negative links. Then, it strategically selects beneficial candidate edges to avoid the introduction of new unbalanced triangles. Finally, SGA introduces a curriculum learning strategy based on edge difficulty scores. These scores quantify the likelihood of an edge belonging to an unbalanced triangle, prioritizing balanced edges during training to improve model performance and reduce the negative impact of noisy data. This framework, therefore, combines structural augmentation and a novel data augmentation perspective, demonstrating significant improvements in link sign prediction across several real-world datasets. Its effectiveness is supported by experimental results showing performance improvements of up to 26.2%, highlighting the importance of addressing structural and data-related biases in SGNN training. The theoretical analysis also provides a generalization error bound for the SGNN model, further substantiating the efficacy of the SGA framework.
Generalization Bound#
The concept of a generalization bound in machine learning, particularly within the context of graph neural networks (GNNs), is crucial for understanding a model’s ability to generalize from training data to unseen data. A tighter generalization bound implies better generalization performance. This paper investigates the generalization error bound for Signed Graph Neural Networks (SGNNs), focusing on link sign prediction. The authors demonstrate that random edge dropping (a common data augmentation technique) fails to improve generalization, contradicting prior assumptions. This highlights the importance of developing tailored augmentation techniques for SGNNs, unlike methods effective for other GNN tasks. The theoretical analysis provides insights into the factors influencing the generalization performance of SGNNs and offers a novel perspective on data augmentation strategy. Understanding the relationship between model architecture, data properties (like graph sparsity and triangle balance), and generalization capability is paramount for building robust and reliable SGNN models. This provides a theoretical foundation for future research on data augmentation and model design specifically for SGNNs. The derived generalization bound could also inform the development of regularization strategies or model selection techniques to minimize generalization error.
Experimental Results#
The Experimental Results section of a research paper is crucial for validating the claims and hypotheses presented earlier. A strong Experimental Results section will provide a detailed description of the experiments conducted, including the datasets used, the evaluation metrics employed, and the specific methodology followed. Robust statistical analysis is key, showing not just performance but also its significance (e.g., p-values, confidence intervals). The results should be clearly presented, often using tables and figures to visualize the data effectively. A comparison to baseline or state-of-the-art methods is essential to establish the novelty and improvement of the proposed approach. Moreover, any unexpected or counter-intuitive results should be acknowledged and discussed, demonstrating the researchers’ thoroughness and critical thinking. The analysis should go beyond simply reporting numbers; it needs to interpret the findings in light of the research questions, highlighting key trends and patterns. Finally, limitations of the experimental setup and potential sources of bias should be transparently addressed, strengthening the overall credibility and impact of the research.
Limitations of SGA#
The proposed Signed Graph Augmentation (SGA) framework, while demonstrating effectiveness in improving SGNN performance, has limitations. SGA’s reliance on balance theory might limit its applicability to real-world signed networks that don’t strictly adhere to this theoretical framework. The augmentation strategy may not generalize well to datasets with significantly different structural patterns or those lacking clear positive/negative relationships. The computational cost of SGA, particularly the candidate edge generation and selection process, could hinder its scalability to extremely large graphs. Finally, the effectiveness of SGA’s curriculum learning strategy depends on the accurate calculation of edge difficulty scores, which might be sensitive to hyperparameter tuning and susceptible to noise in the data.
More visual insights#
More on figures

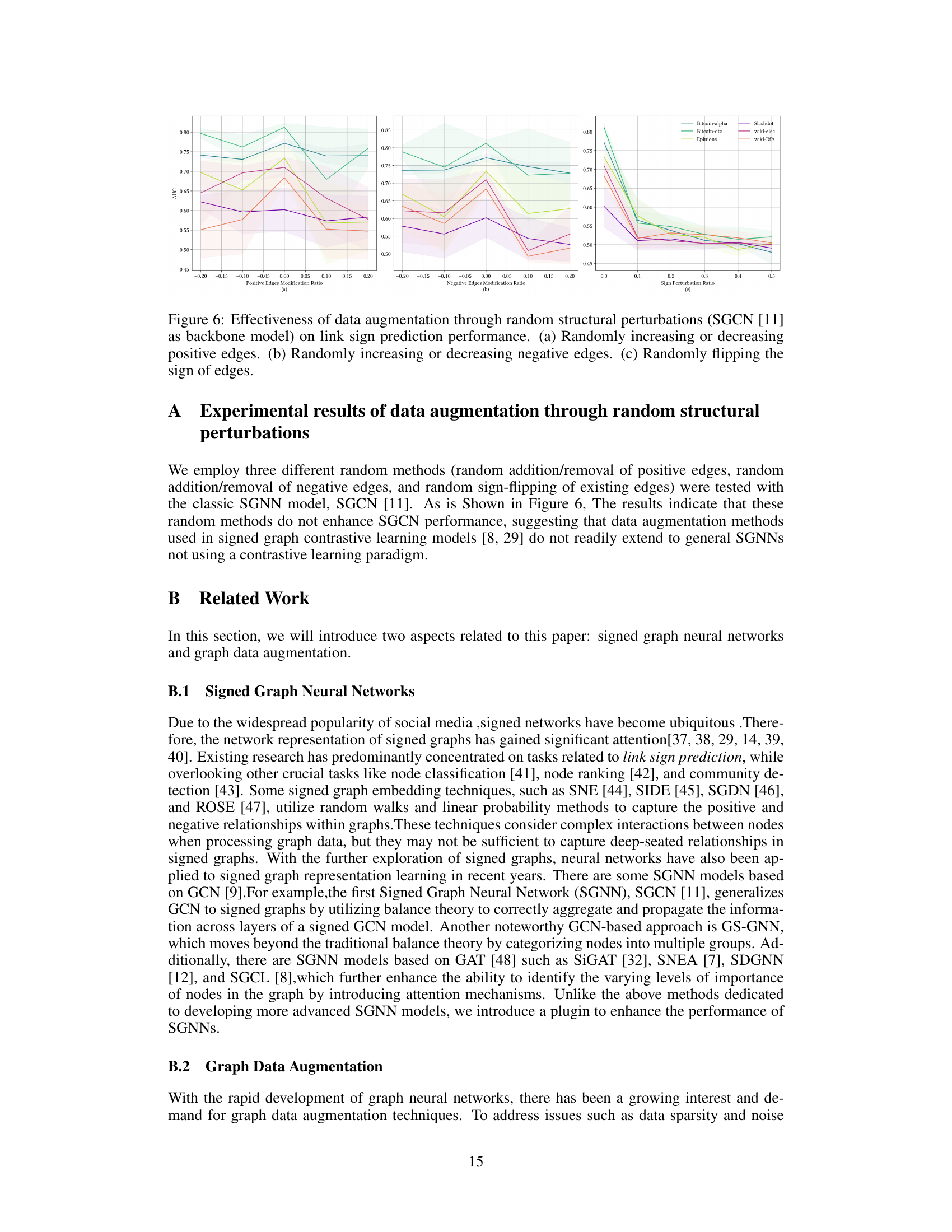
This figure shows the results of experiments using SGCN with three different random structural perturbation methods to augment the training data for link sign prediction. The methods tested are: randomly increasing/decreasing positive edges, randomly increasing/decreasing negative edges, and randomly flipping edge signs. The results demonstrate that none of these random augmentation methods consistently improve SGCN’s performance.

The figure illustrates the three main steps of the Signed Graph Augmentation (SGA) framework: 1) generating candidate training samples by using a Signed Graph Convolutional Network (SGCN) to predict potential edges based on node embeddings and structural balance theory, 2) selecting beneficial candidate samples that do not introduce new unbalanced triangles, and 3) introducing edge difficulty scores as a new feature for training samples which is used in a curriculum learning approach to focus on easier samples first. The framework aims to alleviate the issues of graph sparsity and unbalanced triangles in signed graph neural networks.

This figure presents two case studies from the Bitcoin-alpha dataset to illustrate how SGA improves link sign prediction. Case 1 shows that SGA, by utilizing latent structure, helps SGCN to correctly predict the sign of initially mispredicted edges. Case 2 demonstrates how SGA, by modifying edge signs in existing structures, reduces the impact of unbalanced triangles and enables SGCN to achieve correct prediction results.

The figure shows the results of experiments conducted to evaluate the effectiveness of three different random structural perturbation methods for data augmentation in link sign prediction tasks. The methods are: randomly increasing or decreasing positive edges; randomly increasing or decreasing negative edges; and randomly flipping the sign of edges. The results, based on the SGCN model, indicate that none of these random perturbation methods consistently improve performance.
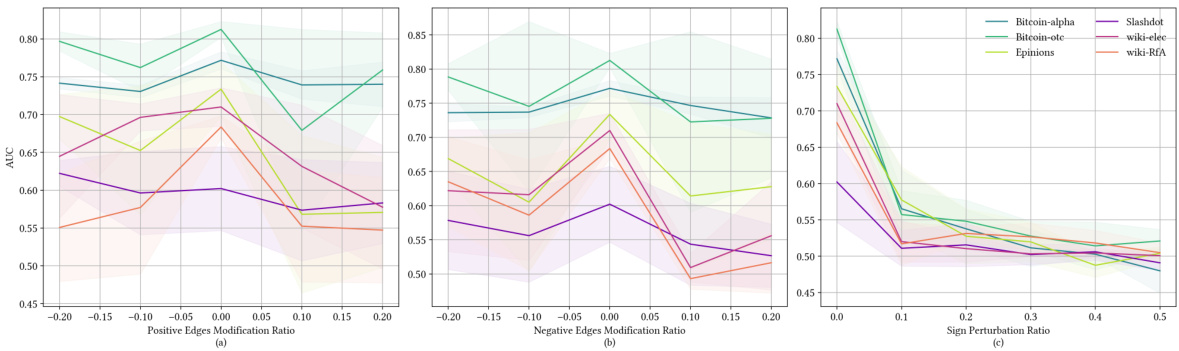
This figure displays the results of experiments testing the effectiveness of three different random structural perturbation methods for data augmentation on a link sign prediction task using the SGCN model. The methods tested were: randomly increasing or decreasing the number of positive edges, randomly increasing or decreasing the number of negative edges, and randomly flipping the sign of existing edges. The results, shown across six different datasets, demonstrate that none of these random perturbation methods consistently improved the SGCN model’s performance on this task. This suggests that simple random structural perturbations are not an effective data augmentation strategy for signed graph neural networks.
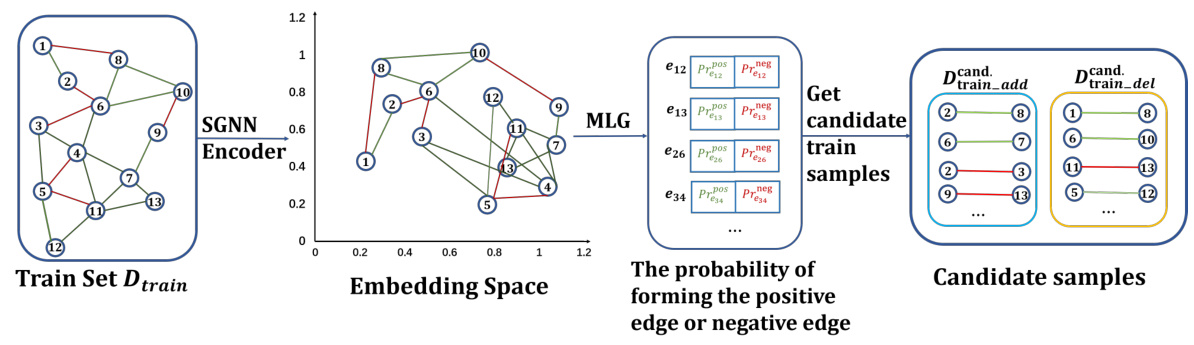
The figure illustrates the overall process of the Signed Graph Augmentation (SGA) framework. It comprises three main stages: 1. Generating candidate training samples using a pre-trained SGNN to project nodes into an embedding space and predict the probability of forming positive or negative edges. 2. Selecting beneficial candidates by prioritizing those that don’t introduce new unbalanced triangles and removing existing unbalanced ones. 3. Introducing a new feature (edge difficulty score) for training samples, influencing the training weight of edges based on their difficulty scores in a curriculum learning approach to mitigate the negative impact of unbalanced triangles. The figure uses color-coded lines (green for positive edges, red for negative edges) to visually represent the edge signs and their changes throughout the process.
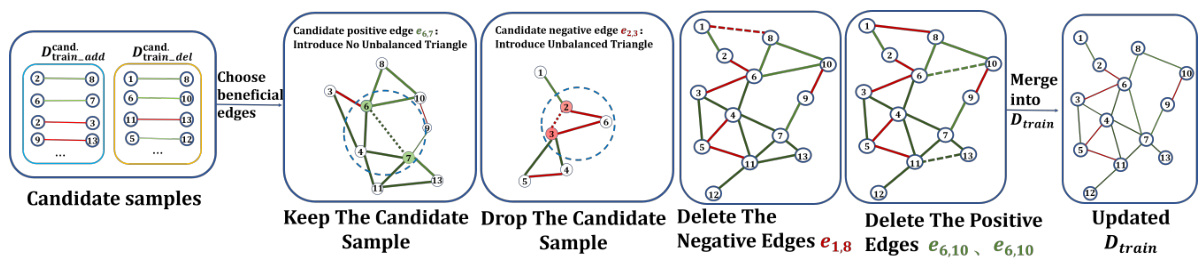
This figure illustrates the three main steps of the Signed Graph Augmentation (SGA) framework. First, it generates candidate training samples by using a pre-trained SGNN model to predict potential positive and negative edges based on node embeddings. The predicted edges are then filtered to select only those that don’t introduce new unbalanced triangles, ensuring that SGA doesn’t negatively impact training. Finally, new features, specifically edge difficulty scores, are introduced to the training samples. These difficulty scores are used in a curriculum learning approach, starting with easier edges (edges in balanced triangles) and progressing to harder edges (edges in unbalanced triangles) during training to improve SGNN performance. The figure uses color-coded lines to visualize positive (green) and negative (red) edges.

This figure illustrates the three main stages of the Signed Graph Augmentation (SGA) framework: generating candidate samples, selecting beneficial candidates, and introducing new features. The first stage uses a pre-trained Signed Graph Convolutional Network (SGCN) to predict potential edges in the graph based on node embeddings. The second stage filters these candidates, keeping only those that do not introduce new unbalanced triangles. The final stage assigns each edge a difficulty score based on its contribution to unbalanced triangles and incorporates a curriculum-based training schedule. This process aims to improve the training of SGNNs by addressing issues of graph sparsity and unbalanced triangles.
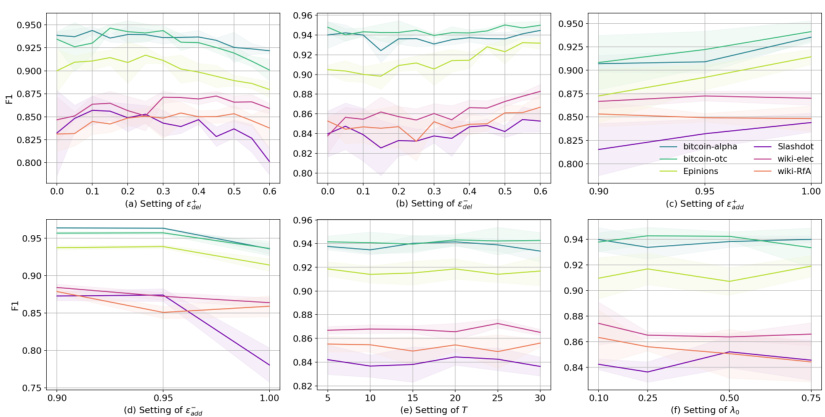
The figure displays the results of experiments assessing the impact of three different random structural perturbation methods on link sign prediction using SGCN as the backbone model. Each subfigure shows the F1 score across six real-world datasets, varying the rate of positive edge modification (a), negative edge modification (b), and sign flipping (c). The results demonstrate that none of these random methods consistently improves SGCN performance.

This figure displays the results of experiments evaluating the effectiveness of three different random structural perturbation methods for data augmentation on link sign prediction using the SGCN model. The three methods are: (a) randomly modifying the number of positive edges, (b) randomly modifying the number of negative edges, and (c) randomly flipping the signs of existing edges. The results show that none of these methods consistently improve SGCN’s performance across different datasets. This indicates the limitations of simple random structural perturbations for data augmentation in this specific task.
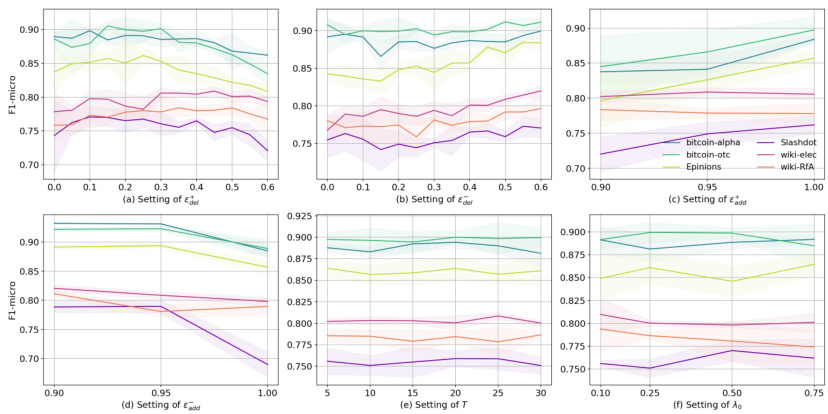
This figure shows the results of experiments using three different random structural perturbation methods on the link sign prediction task using SGCN as the backbone model. The methods tested were randomly increasing/decreasing positive edges, randomly increasing/decreasing negative edges, and randomly flipping the sign of existing edges. The results demonstrate that none of these methods consistently improve the performance of SGCN, suggesting that these data augmentation techniques are not effective for SGNNs.
More on tables

This table shows the density of six real-world datasets before and after applying the proposed Signed Graph Augmentation (SGA) method. Density is a measure of how many edges are present in a graph compared to the maximum possible number of edges. A higher density suggests a more connected graph. This table demonstrates that SGA increases the density of all six datasets, implying that it makes these graphs more connected.
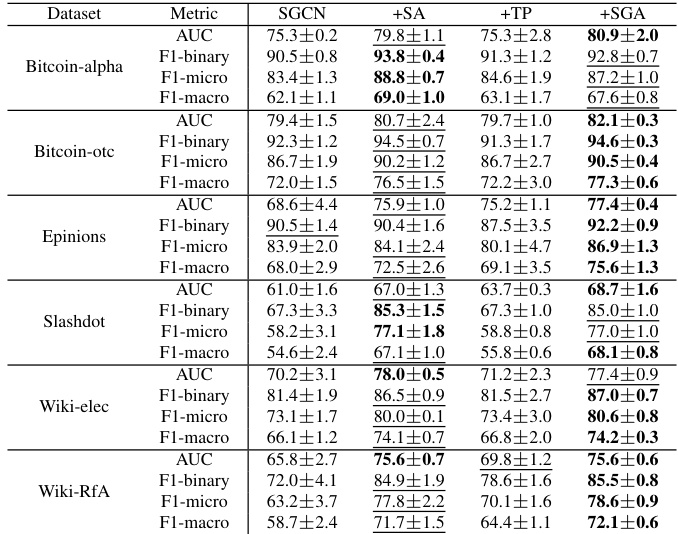
This table presents the ablation study results, showing the performance of SGCN with different combinations of the proposed SGA framework components (Structure Augmentation, Training Plan, and the complete SGA) across six benchmark datasets. The metrics used are AUC, F1-binary, F1-micro, and F1-macro. The table shows the improvement in performance achieved by each component of the SGA individually and in combination.

This table shows the number of nodes, links, positive edges, negative edges, and density for six real-world datasets used in the paper: Bitcoin-OTC, Bitcoin-Alpha, Wiki-elec, Wiki-RfA, Epinions, and Slashdot. These statistics provide context for the size and characteristics of the graphs used to evaluate the proposed Signed Graph Augmentation (SGA) framework.
This table presents the results of link sign prediction experiments conducted on six benchmark datasets using five different graph neural network models (GCN, GAT, SGCN, SiGAT, GS-GNN). Each model’s performance is evaluated with and without the proposed Signed Graph Augmentation (SGA) framework. The results are reported as the average and standard deviation of AUC (Area Under the ROC Curve) and F1-binary scores across five independent runs on each dataset. The improvement achieved by integrating the SGA framework is also shown for each model.
Full paper#