TL;DR#
Quantizing large language models reduces computational cost but often sacrifices accuracy. Existing solutions for mitigating the resulting quantization error have limitations; they either make strong assumptions or only partially solve the problem. The cumulative nature of quantization errors distorts the sampling trajectory, reducing overall model performance.
This paper introduces StepbaQ, a method that calibrates the sampling trajectory by treating quantization errors as a ‘stepback’ in the denoising process. StepbaQ uses a sampling step correction mechanism, solely relying on statistics from a small calibration dataset to counteract the adverse effects of accumulated quantization errors. Experimental results demonstrate significant performance gains on various models and settings, making StepbaQ a practical and effective plug-and-play technique for enhancing quantized diffusion models.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses a critical challenge in deploying large language models on resource-constrained devices. Quantization, while effective for compression, can significantly reduce accuracy. The proposed StepbaQ method offers a novel solution by correcting sampling trajectory errors, improving performance without altering existing quantization settings. This opens up new avenues for efficient and accurate model deployment on mobile devices.
Visual Insights#
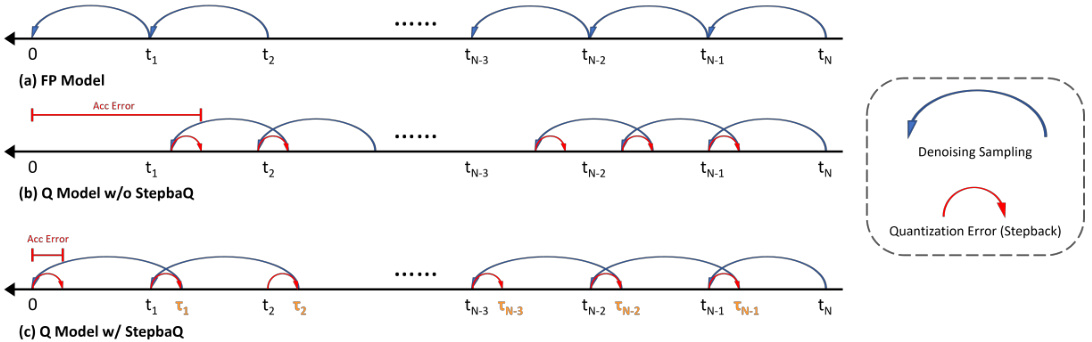
🔼 This figure illustrates the denoising process in three scenarios: (a) A floating-point (FP) model showing the ideal, error-free process. (b) A quantized (Q) model without StepbaQ correction shows how quantization errors accumulate and distort the sampling trajectory. (c) A quantized (Q) model with StepbaQ demonstrates the method’s correction mechanism that reduces the effect of accumulated error by adjusting the sampling steps.
read the caption
Figure 1: Overview of the denoising process of StepbaQ and existing methods. Figure (a) shows the original denoising process. Figure (b) demonstrates the negative impact of quantization error without changing the step size, leading to significant accumulation error. Figure (c), on the other hand, illustrates how StepbaQ treats the quantization error as a stepback in the denoising process and adopts corrected steps with a larger step size to eliminate cumulative quantization error.
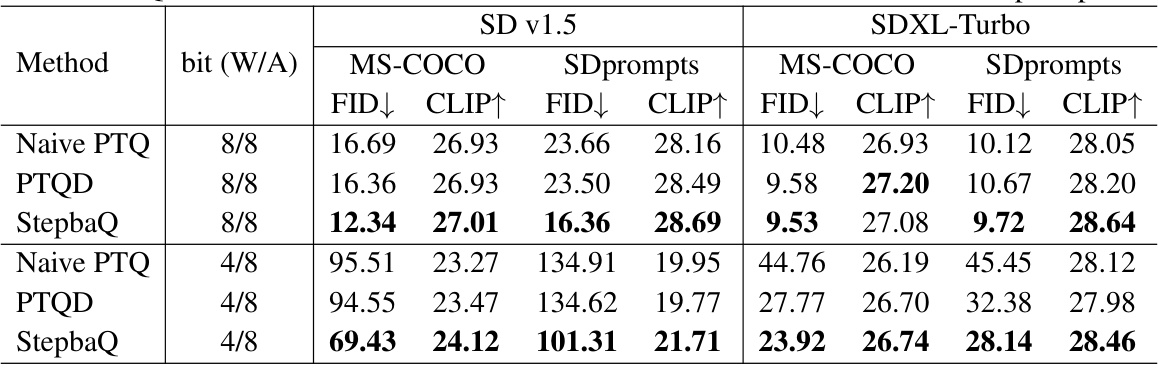
🔼 This table presents the results of applying different quantization methods (Naive PTQ, PTQD, and StepbaQ) to two different diffusion models, Stable Diffusion v1.5 and SDXL-Turbo. The models are quantized using two different bit-width settings (W8A8 and W4A8), and their performance is evaluated on two datasets, MS-COCO and SDprompts, using FID and CLIP scores. This allows for a comparison of the effectiveness of the different quantization methods in maintaining the quality of the generated images after quantization.
read the caption
Table 1: Quantization results of SD v1.5 and SDXL-Turbo on MS-COCO and SDprompts.
In-depth insights#
Quantization’s Pitfalls#
Quantization, while offering benefits in model compression and efficiency, presents several significant challenges. The cumulative nature of quantization errors is a major pitfall; small individual errors accumulate over multiple steps in processes like diffusion models, leading to substantial degradation in final output quality. This is particularly problematic because the errors compound in ways that are not easily predicted or corrected through simple methods. Addressing this accumulation requires sophisticated techniques that go beyond minimizing individual quantization errors. Varying activation ranges across different steps further complicate the process. This necessitates careful calibration or adaptive quantization strategies, adding complexity to the implementation. Finally, the choice of quantization scheme and parameters has a substantial impact on the resulting performance. The optimal choice often depends on the specific model architecture, task and hardware constraints, and may require extensive experimentation. Overall, effectively mitigating these pitfalls demands a holistic approach that takes into account the inherent complexities of quantization within the target application.
StepbaQ: A New Method#
StepbaQ, introduced as a novel method, tackles the challenge of accumulated quantization error in diffusion models. It conceptualizes quantization error as a ‘stepback’ in the denoising process, thus providing a new perspective on the issue. Instead of directly correcting errors, StepbaQ calibrates the sampling trajectory to counteract the adverse effects. A key strength lies in its reliance on readily available statistics of quantization errors derived from a small calibration dataset, making it highly applicable and easily integrated with existing frameworks as a plug-and-play solution. The method’s effectiveness is demonstrated through significant performance improvements in quantized models, showcasing its capacity to enhance the quality of generated samples without modifying quantization settings. This makes StepbaQ a valuable contribution to the field of quantized diffusion models by offering a general and efficient approach to mitigate accumulated quantization errors.
Temporal Error Impact#
The concept of “Temporal Error Impact” in a quantized diffusion model centers on how the cumulative effect of quantization errors across multiple sampling steps alters the model’s performance. Initial quantization errors, while individually small, accumulate over time, leading to a significant deviation from the ideal sampling trajectory. This deviation isn’t simply an increase in overall error; it’s a temporal distortion, causing a shift in the latent space representation at each step. This shift is analogous to taking a “step back” in the denoising process, hindering the model’s ability to accurately reconstruct the desired image. The consequence is a degradation in image quality, evidenced by increased FID (Fréchet Inception Distance) scores, and potentially a loss of diversity in generated samples. The crucial aspect is that the impact isn’t linear; small early errors create a snowball effect, magnifying the subsequent errors and drastically affecting final image generation. Therefore, addressing temporal error accumulation is essential for improving the performance of quantized diffusion models. Strategies for mitigation need to consider this cumulative effect rather than just focusing on minimizing error at each individual step.
Step Size Adaptation#
Step size adaptation in quantized diffusion models addresses the challenge of accumulated quantization error. Standard diffusion model sampling involves a predetermined schedule of steps, but quantization introduces noise that distorts this trajectory. Larger steps counteract this effect by effectively “skipping over” regions where quantization error is significant. The method is crucial because smaller steps amplify the cumulative error, leading to degraded sample quality. Step size adaptation is implemented by dynamically adjusting the sampling schedule based on the magnitude of observed quantization error, effectively improving accuracy in a plug-and-play manner for existing quantization frameworks, and enhancing overall performance. The key is to balance step size with the degree of error; too large a step risks instability, too small and the error accumulates. Careful calibration is needed to determine the optimal adaptive strategy and to ensure compatibility with various diffusion samplers (DDIM, Euler-a, etc.).
Future Research#
Future research directions stemming from this work on quantized diffusion models could explore several promising avenues. Improving the efficiency of StepbaQ itself is crucial, potentially through more sophisticated error modeling or more efficient calibration methods. Extending StepbaQ to single-step samplers, such as those used in accelerated inference, presents a significant challenge that warrants dedicated research. The current assumption of Gaussian quantization errors might be relaxed to better accommodate real-world scenarios, and further investigation of alternative quantization techniques that inherently reduce error accumulation would be valuable. Finally, exploring the applicability of StepbaQ to diverse diffusion model architectures and tasks beyond image generation, including other modalities like audio or video, could unlock significant advancements in efficient deep generative modeling.
More visual insights#
More on figures

🔼 This figure compares three denoising processes: (a) the original floating point process, (b) a quantized process without StepbaQ showing error accumulation, and (c) a quantized process with StepbaQ which corrects the sampling trajectory. StepbaQ addresses quantization error by treating it as a ‘stepback’ and correcting the sampling trajectory with larger steps to mitigate accumulated error.
read the caption
Figure 1: Overview of the denoising process of StepbaQ and existing methods. Figure (a) shows the original denoising process. Figure (b) demonstrates the negative impact of quantization error without changing the step size, leading to significant accumulation error. Figure (c), on the other hand, illustrates how StepbaQ treats the quantization error as a stepback in the denoising process and adopts corrected steps with a larger step size to eliminate cumulative quantization error.
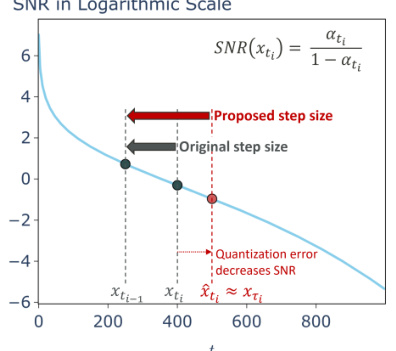
🔼 The figure shows the signal-to-noise ratio (SNR) curve for a diffusion process. The blue curve represents the ideal SNR. The black dots and arrows indicate how quantization error reduces SNR and how StepbaQ compensates by taking a larger step to reach the intended SNR, addressing the ‘stepback’ effect of quantization error.
read the caption
Figure 2: SNR curve of diffusion process. The quantization error decreases the SNR, which could be regarded as a stepback. To address this issue, StepbaQ takes a larger step to reach the scheduled SNR.
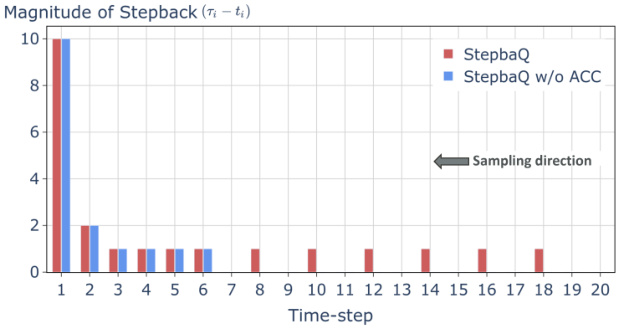
🔼 This figure shows a bar chart illustrating the magnitude of stepback (the difference between the corrected step and the original step) for each sampling step when using the StepbaQ method on the Stable Diffusion v1.5 model with the W8A8 quantization setting. The chart compares StepbaQ’s corrections to a version of the algorithm without error accumulation consideration. It highlights that most corrections happen in the later sampling steps, implying that accumulated quantization error significantly affects the final sample quality. StepbaQ’s approach, which accounts for error accumulation, makes corrections more frequently than the algorithm without this feature.
read the caption
Figure 3: Magnitude of stepback for SD v1.5 on the SD-prompts dataset under W8A8 setting. Most sampling step corrections occur at the last few steps of sampling, showing the importance of these steps. Since StepbaQ considers the error accumulation, it performs corrections more frequently than StepbaQ w/o ACC.

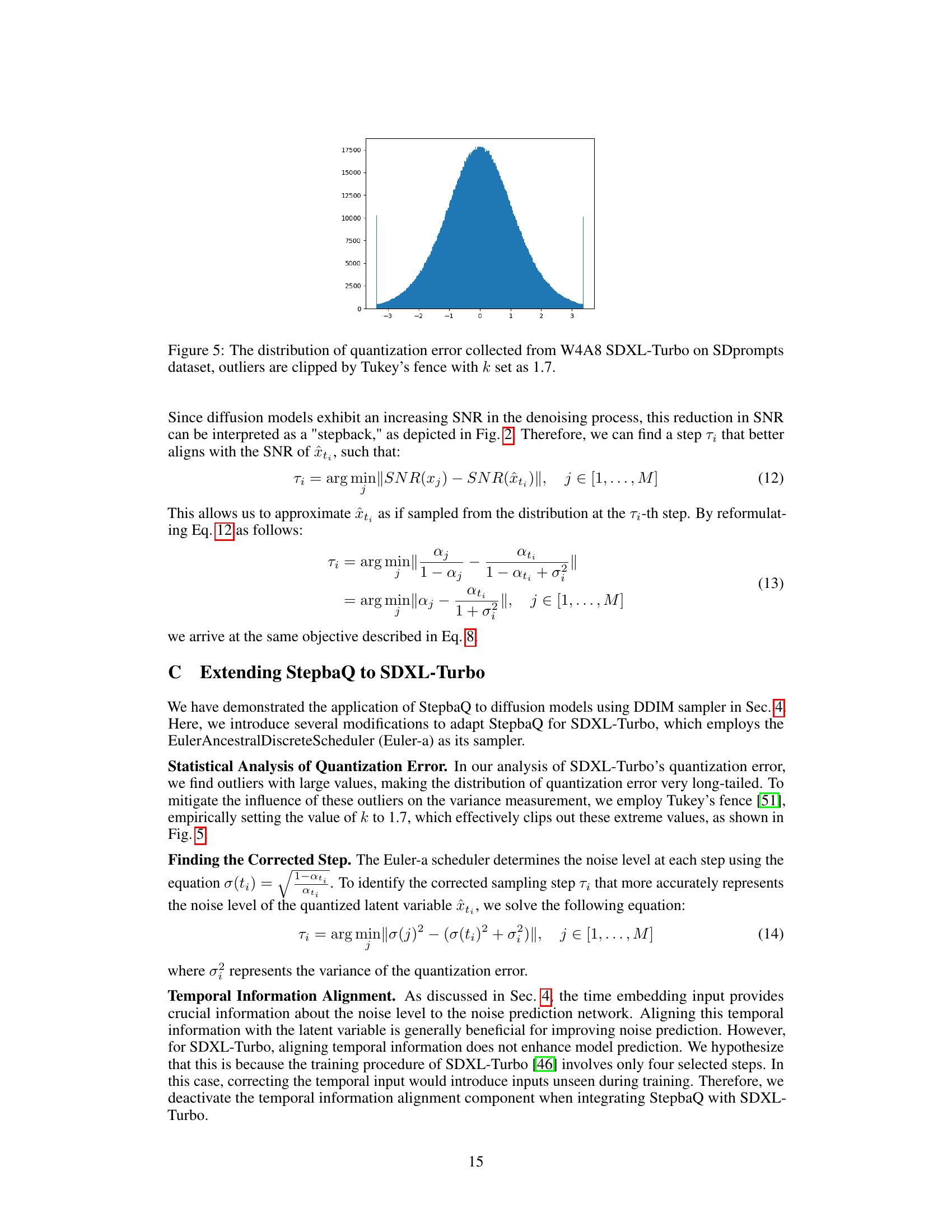
🔼 This figure displays the distribution of quantization errors observed for three different diffusion models (SDv1.4, SDv1.5, and SDXL-Turbo) under the W8A8 quantization setting. Each subfigure shows a histogram representing the frequency of different quantization error values for a given model. The distributions generally exhibit a bell shape, centered around zero, indicating that the mean quantization error is close to zero. However, there are differences in the spread or variance of the distributions, suggesting that some models may be more sensitive to quantization than others. This visual representation supports the paper’s analysis of the quantization error and its assumption that this error follows a Gaussian distribution, though with potentially fatter tails than a purely Gaussian distribution.
read the caption
Figure 4: The distribution of quantization errors collected under W8A8 setting.

🔼 The figure shows the distribution of quantization errors obtained from the SDXL-Turbo model under the W4A8 setting using the SDprompts dataset. To mitigate the impact of outliers, the data has been pre-processed using Tukey’s fence with a k-value of 1.7, which helps remove extreme values and provide a clearer view of the distribution’s central tendency and spread. This visualization helps confirm assumptions made in the paper about the distribution of quantization errors.
read the caption
Figure 5: The distribution of quantization error collected from W4A8 SDXL-Turbo on SDprompts dataset, outliers are clipped by Tukey’s fence with k set as 1.7.

🔼 This figure displays a qualitative comparison of images generated by the Stable Diffusion v1.5 model under different quantization methods. The first column shows images generated using the full-precision (FP) model, while subsequent columns illustrate results using Naive PTQ, PTQD, and StepbaQ. Each row presents a different image prompt or subject. The goal is to visually compare the quality of images generated under each method. The figure aims to visually demonstrate that StepbaQ provides a better preservation of image quality when comparing to other quantization methods, especially with regards to visual artifacts.
read the caption
Figure 6: Qualitative results of SD v1.5 on SDprompts under W8A8 setting.

🔼 This figure displays qualitative results of the SDXL-Turbo model on the SDprompts dataset under the W4A8 quantization setting. It compares the image generation quality of the floating-point model (FP) against those generated by the Naive PTQ, PTQD, and StepbaQ methods. Each row presents a different prompt, with four columns showing the results of each method. The purpose is to visually demonstrate how StepbaQ improves the generation quality of quantized diffusion models compared to other methods, particularly highlighting the mitigation of visual artifacts resulting from quantization errors.
read the caption
Figure 7: Qualitative results of SDXL-Turbo on SDprompts under W4A8 setting.

🔼 This figure displays the qualitative comparison of images generated by different methods on the SDprompts dataset under W4A8 setting. It compares the original floating-point model (FP) with results from Q-Diffusion, PTQD, TFMQ, and StepbaQ, showcasing the visual differences between different quantization methods and their impacts on image quality. StepbaQ shows the best visual quality, closely matching the floating-point model.
read the caption
Figure 8: Qualitative results of SD v1.4 on SDprompts under W4A8 setting.
More on tables
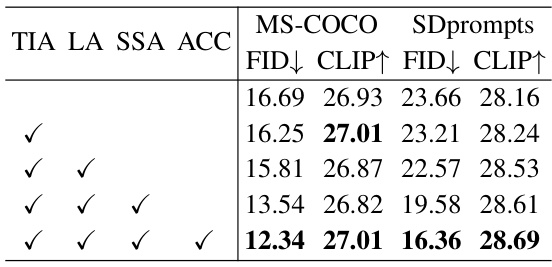
🔼 This table presents the results of an ablation study conducted on the Stable Diffusion v1.5 model using the W8A8 quantization setting. The study investigates the impact of different components of the proposed StepbaQ method on the model’s performance, as measured by FID and CLIP scores on the MS-COCO and SDprompts datasets. The components are Temporal Information Alignment (TIA), Latent Adjustment (LA), Step Size Adaptation (SSA), and Error Accumulation (ACC). Each row represents a different combination of these components, showing the effect of including or excluding each one on the final FID and CLIP scores.
read the caption
Table 2: Ablation Study of SD v1.5 on MS-COCO and SDprompts under W8A8 setting.
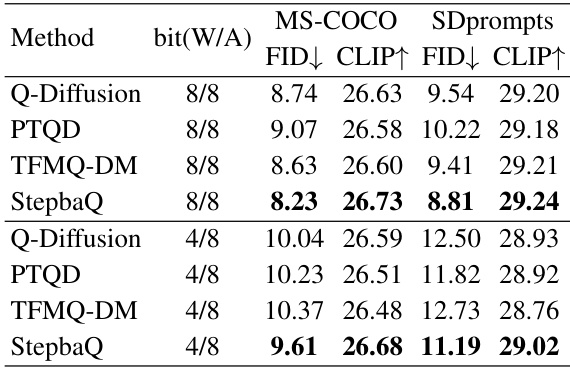
🔼 This table presents the results of applying different quantization methods (Naive PTQ, PTQD, and StepbaQ) to two different Stable Diffusion models (SD v1.5 and SDXL-Turbo) under two different quantization settings (W8A8 and W4A8). The performance is measured using FID (Fréchet Inception Distance) and CLIP (Contrastive Language-Image Pre-training) scores on two datasets: MS-COCO and SDprompts. Lower FID indicates better image quality and higher CLIP score indicates better alignment between the generated images and their text prompts.
read the caption
Table 1: Quantization results of SD v1.5 and SDXL-Turbo on MS-COCO and SDprompts.

🔼 This table presents the kurtosis and skewness of the quantization errors for three different diffusion models (SDv1.4, SDv1.5, and SDXL-Turbo) under the W8A8 quantization setting. Kurtosis measures the ’tailedness’ of the distribution, while skewness measures its asymmetry. These statistics provide insights into the shape of the quantization error distribution and how it deviates from a normal distribution.
read the caption
Table 4: The kurtosis and skewness of the quantization errors collected under W8A8 setting.
Full paper#