↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many modern applications rely on large datasets from numerous sources. However, transmitting this data directly poses significant privacy risks. Differential Privacy (DP) mechanisms add noise to the data to protect individual privacy, but this can significantly increase communication costs. Existing methods for compressing DP mechanisms either approximate the original distribution or only work for specific types of noise, limiting their applicability.
This paper introduces Poisson Private Representation (PPR), a novel method that exactly compresses any local DP mechanism while ensuring local DP. PPR uses shared randomness and a Poisson process for efficient compression and recovery, achieving a compression size within a logarithmic gap from the theoretical lower bound. Crucially, it preserves the statistical properties of the original mechanism, such as unbiasedness and Gaussianity. The authors demonstrate PPR’s effectiveness on distributed mean estimation, showcasing its superior trade-off compared to existing methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on differential privacy and distributed systems. It offers a novel solution for compressing differentially private mechanisms, reducing communication costs while maintaining privacy guarantees. This opens new avenues for research in privacy-preserving distributed machine learning and other applications where communication is a bottleneck.
Visual Insights#
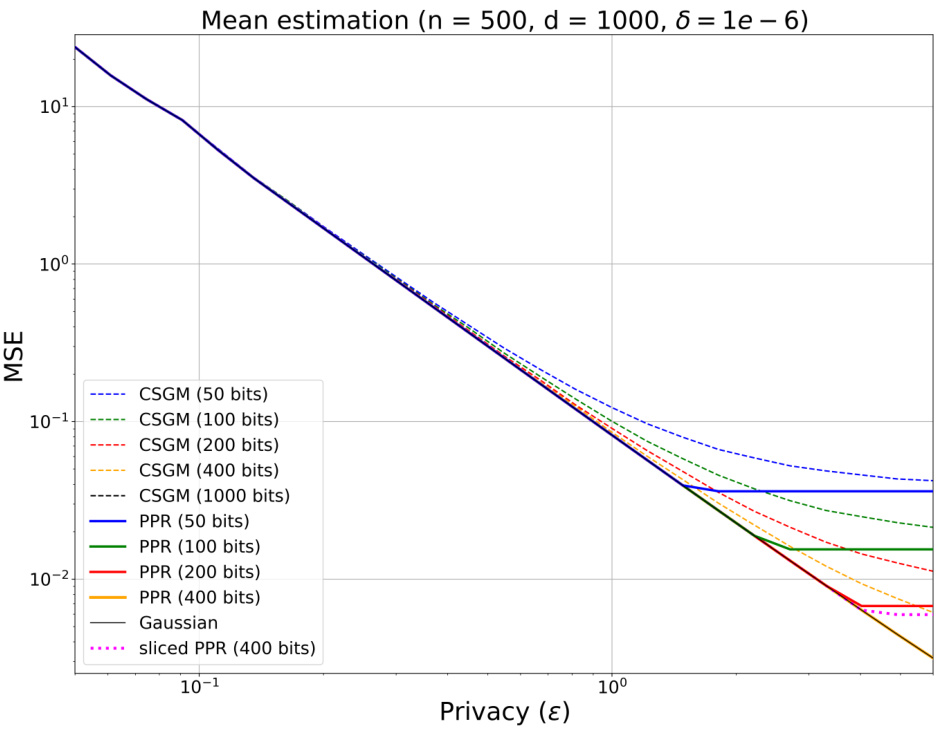
The figure compares the mean squared error (MSE) of distributed mean estimation using Poisson Private Representation (PPR) and Coordinate Subsampled Gaussian Mechanism (CSGM) for various privacy parameters (ε) and compression sizes. It shows that PPR consistently achieves lower MSE than CSGM across different privacy levels and compression rates, highlighting its superior performance in terms of privacy-accuracy-communication trade-offs. The figure also demonstrates that PPR’s performance closely matches the uncompressed Gaussian mechanism, showcasing the effectiveness of its exact simulation approach. The ‘sliced PPR’ results indicate a slight MSE increase but still outperforms CSGM.
In-depth insights#
PPR:Mechanism#
The Poisson Private Representation (PPR) mechanism offers a novel approach to compressing differentially private mechanisms. Its universality allows it to simulate various local randomizers, unlike previous methods. The exactness of PPR ensures that it perfectly preserves the statistical properties of the original mechanism, a key advantage over simulation-based methods. This accuracy is crucial for applications requiring specific statistical properties like unbiasedness. Furthermore, PPR’s efficiency in compressing outputs is highlighted by its near-optimal compression size, a logarithmic gap from the theoretical lower bound. This is achieved through the use of shared randomness and a randomized encoder, preserving local differential privacy while maintaining strong central DP guarantees. This combination of universality, exactness, and efficiency makes PPR a powerful tool for various privacy-preserving applications, particularly in distributed settings where communication cost is a major concern.
DP Compression#
Differential privacy (DP) mechanisms are crucial for protecting sensitive data, but they often lead to large communication overheads. DP compression techniques aim to reduce this overhead by compressing DP outputs without significantly compromising privacy guarantees. The core challenge is balancing the compression rate with the preservation of DP’s statistical properties. Lossless compression methods strive to perfectly reconstruct the original DP output, while lossy methods accept some information loss in exchange for higher compression. A key aspect is the type of DP used—local DP, where data is randomized before leaving the device, and central DP, where the aggregator performs the randomization. The trade-off between compression, privacy, and accuracy is critical. Novel methods like Poisson Private Representation (PPR) explore ways to achieve exact simulation of DP mechanisms, optimizing the communication cost. However, computational complexity often increases with the desired level of accuracy. The field is actively researching efficient algorithms to improve compression without sacrificing the privacy safeguards of DP.
DME: Experiments#
A hypothetical section titled ‘DME: Experiments’ in a research paper would likely detail empirical evaluations of a distributed mean estimation (DME) algorithm. This would involve defining the experimental setup, including datasets used, the number of distributed nodes, and data characteristics. The experiments should rigorously compare the proposed DME algorithm against existing baselines under varying conditions, such as different levels of privacy (epsilon and delta parameters), communication bandwidth constraints, and data distributions. Key performance metrics, including accuracy (e.g., mean squared error) and communication cost (bits transmitted per node), would be presented and analyzed. Statistical significance testing would be essential to validate the observed results and ensure that improvements are not due to random chance. Furthermore, the results should be visually presented using graphs to show the trade-offs between privacy, accuracy, and communication efficiency. Finally, the discussion should analyze the observed trends, emphasizing strengths, weaknesses, and potential areas for future improvement of the algorithm.
PPR Limitations#
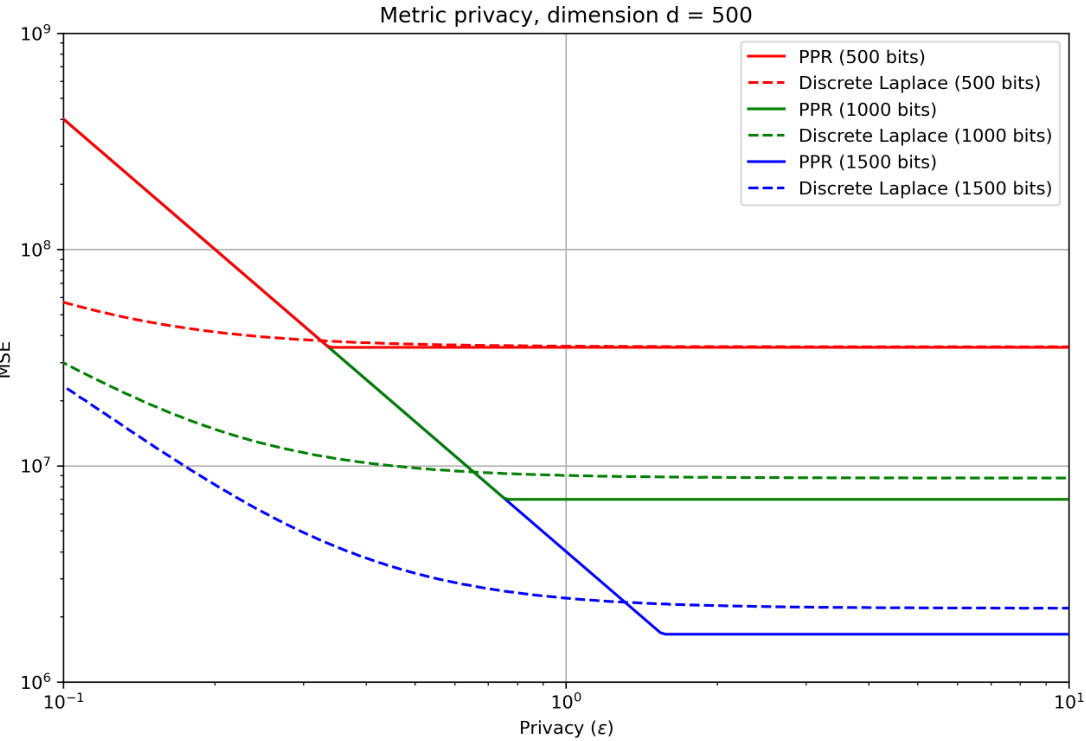
The Poisson Private Representation (PPR) method, while offering significant advantages in compressing differentially private mechanisms, is not without limitations. A primary concern is the computational cost, with the running time scaling exponentially with mutual information. This poses a significant challenge for high-dimensional data or complex mechanisms, although the authors propose a practical solution using a sliced approach. The exponential running time is inherent to exact simulation and may not be avoidable in general. While PPR achieves a logarithmic gap from the theoretical compression lower bound, the actual compression attained could still be substantial, requiring a trade-off between privacy, accuracy, and communication efficiency. The practical implementation necessitates truncation, potentially introducing a small degree of bias and impacting the theoretical guarantees. Finally, although the PPR method itself does not reveal the chosen privacy mechanism, the compressed output might still leak information if other channels of information exist in the system. The authors explicitly highlight these points in their analysis, suggesting areas for future work in optimizing the efficiency and robustness of PPR.
Future of PPR#
The future of Poisson Private Representation (PPR) hinges on addressing its computational complexity. While PPR offers theoretically optimal compression for differentially private mechanisms, its runtime scales exponentially with mutual information, limiting practicality for high-dimensional data. Future work should explore approximation techniques to reduce this complexity without significantly sacrificing accuracy or privacy guarantees. This could involve investigating optimized sampling strategies, exploring the use of low-complexity proposal distributions, or developing hierarchical or incremental approaches. Furthermore, research into the specific applications of PPR is crucial. Exploring its effectiveness in various privacy settings (e.g., beyond local differential privacy) and diverse data modalities would broaden its applicability. Finally, combining PPR with other compression techniques and privacy amplification methods might yield even better trade-offs between communication, accuracy, and privacy. Rigorous empirical evaluations on large-scale datasets, especially concerning the effectiveness of approximation methods, are critical to establish PPR’s practical value.
More visual insights#
More on figures
This figure compares the mean squared error (MSE) of distributed mean estimation using PPR (Poisson Private Representation) and CSGM (Coordinate Subsampled Gaussian Mechanism) for different privacy parameters (ε). It demonstrates the tradeoff between privacy and accuracy and shows PPR consistently outperforms CSGM across different compression sizes. The plot shows that PPR achieves better MSE for various privacy parameters (ε) and compression sizes. For example, for ε = 1 with 50 bits compression, CSGM has an MSE of 0.1231 while PPR has 0.08173, a significant reduction of 33.61%. Also, for a high compression rate at ε=0.5 (25 bits compression), PPR achieves a 22.33% reduction in MSE. It highlights that PPR provides superior trade-off between privacy and accuracy compared to CSGM.

This figure compares the mean squared error (MSE) of distributed mean estimation using Poisson Private Representation (PPR) and Coordinate Subsampled Gaussian Mechanism (CSGM) for different privacy parameters (ε). It shows the MSE performance of both methods across various compression sizes, highlighting PPR’s consistent advantage in achieving lower MSE for the same compression level and privacy budget. The results illustrate the better trade-off PPR offers between communication, accuracy, and central differential privacy compared to CSGM.

This figure compares the mean squared error (MSE) of distributed mean estimation using the proposed Poisson Private Representation (PPR) method and the Coordinate Subsampled Gaussian Mechanism (CSGM) for various privacy parameters (ε). The plot shows the MSE values for different compression sizes (bits) for both PPR and CSGM. It demonstrates the trade-off between privacy (ε), compression size, and accuracy (MSE). The results indicate that PPR consistently achieves a lower MSE than CSGM across different privacy levels and compression sizes, showcasing the effectiveness of PPR in balancing privacy and accuracy.

This figure compares the mean squared error (MSE) of distributed mean estimation using Poisson private representation (PPR) and Coordinate Subsampled Gaussian Mechanism (CSGM) under various privacy parameters (ε). The x-axis represents the privacy parameter ε, and the y-axis represents the MSE on a logarithmic scale. Different lines represent different compression sizes. The figure showcases that PPR consistently achieves lower MSE compared to CSGM across different privacy parameters and compression sizes. It also demonstrates that PPR maintains similar performance to the uncompressed Gaussian mechanism with a significantly smaller compression size.
Full paper#



















