Distributional Reinforcement Learning with Regularized Wasserstein Loss

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it introduces Sinkhorn distributional reinforcement learning (SinkhornDRL), a novel approach that addresses key limitations of existing distributional RL algorithms. SinkhornDRL uses Sinkhorn divergence, a regularized Wasserstein loss, offering improvements in stability, multi-dimensional reward handling, and overall performance. This work will be of interest to researchers working on RL algorithm development and improvement, specifically those focusing on distributional methods and optimal transport. It also provides a theoretical foundation for the understanding and advancement of distributional RL.

Visual Insights

#

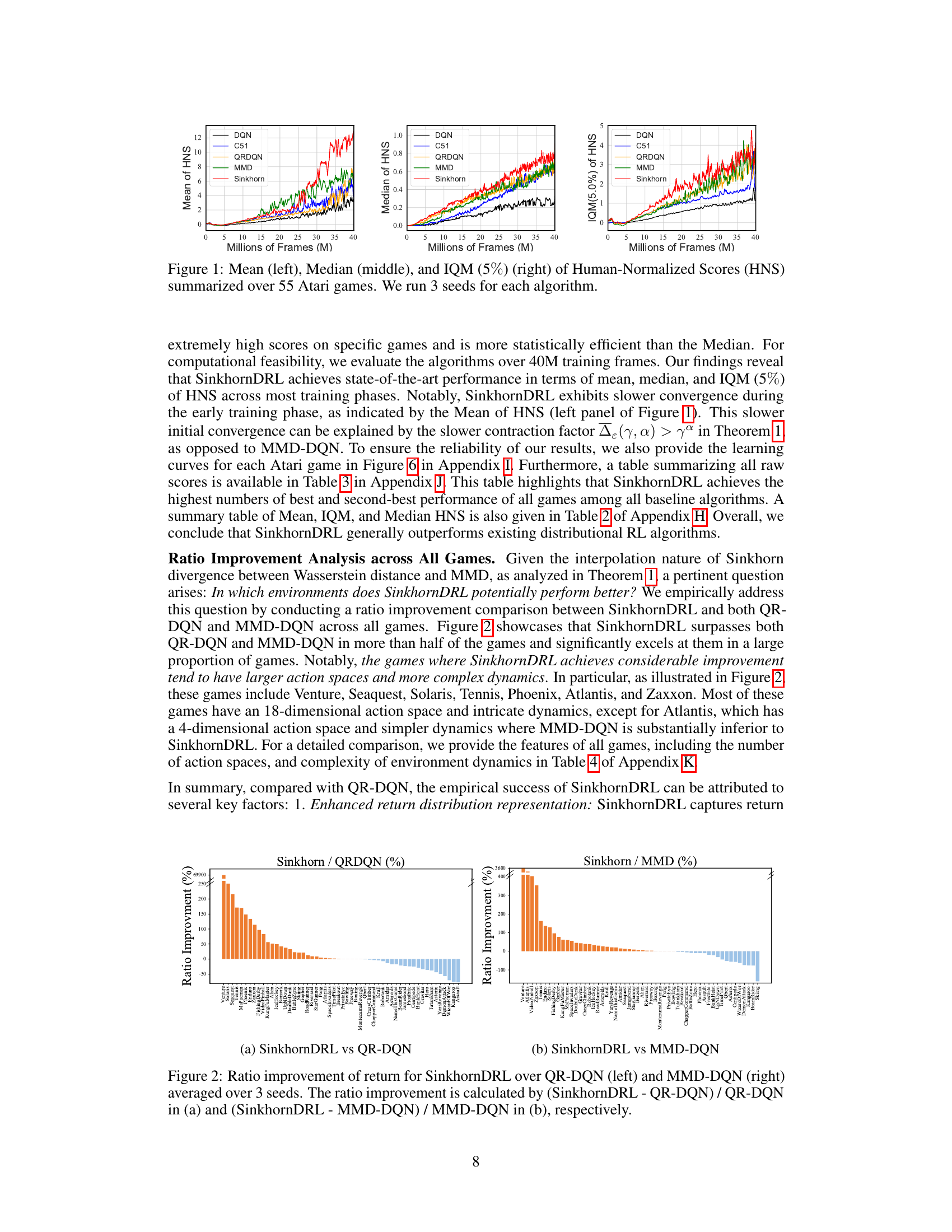
This figure presents a comparison of the performance of five distributional reinforcement learning algorithms (DQN, C51, QR-DQN, MMD-DQN, and SinkhornDRL) across 55 Atari games. The performance is measured using three different metrics: Mean, Median, and Interquartile Mean (IQM) of Human-Normalized Scores (HNS). The x-axis represents millions of training frames, and the y-axis represents the HNS. The figure shows learning curves for each algorithm, averaged over three independent runs (seeds). The shaded areas around the curves represent the standard deviation.

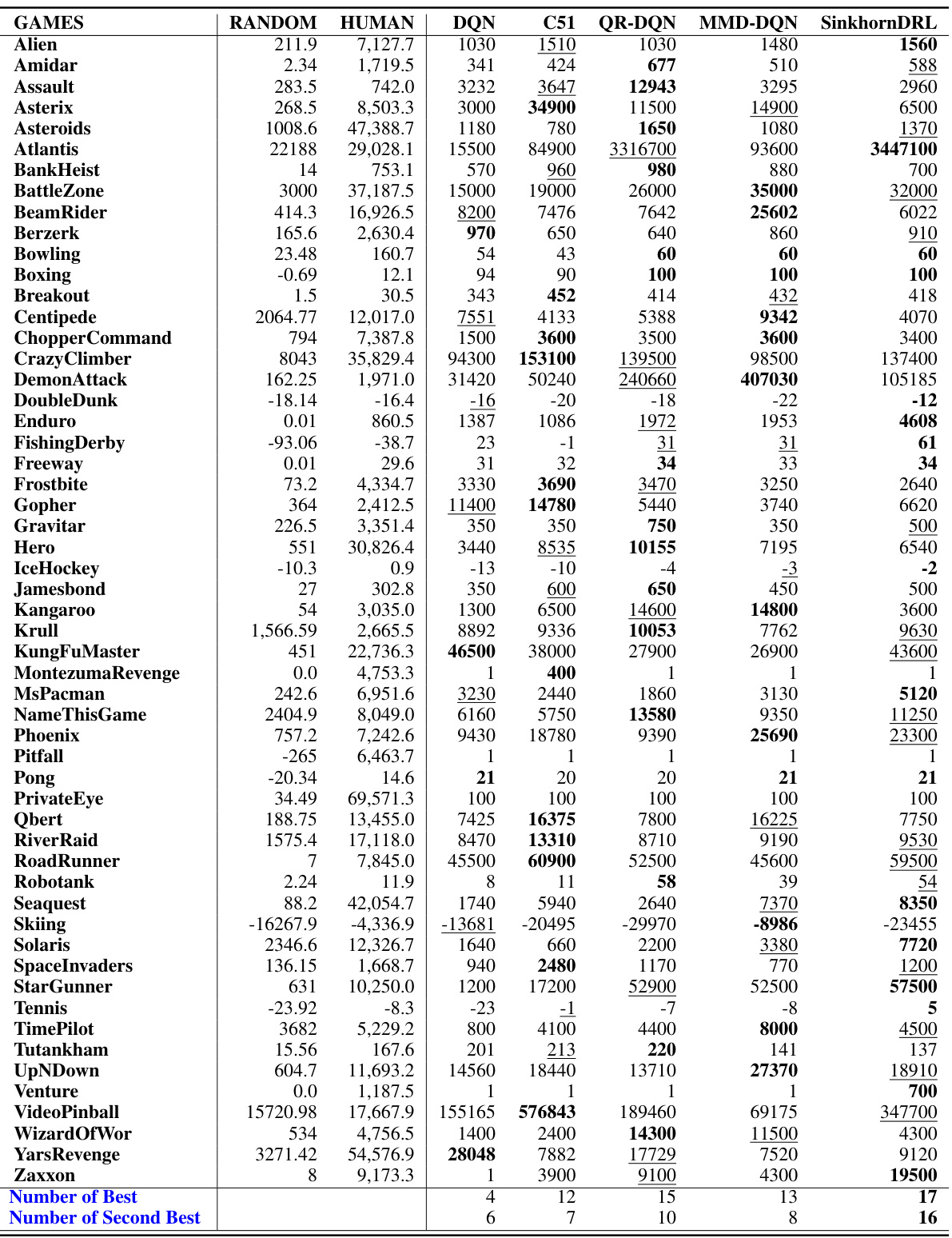
This table compares different distributional reinforcement learning algorithms based on three criteria: the distribution divergence used, the representation of the return distribution (categorical, quantiles, or samples), the convergence rate of the Bellman operator, and the sample complexity of the divergence. It highlights the differences in how various algorithms approach estimating the distribution of returns and the computational cost associated with each.

In-depth insights

#

Sinkhorn Divergence RL

#

The proposed Sinkhorn Divergence RL algorithm offers a novel approach to distributional reinforcement learning by utilizing the Sinkhorn divergence, a regularized Wasserstein distance. This addresses limitations of existing methods, particularly the inaccuracy in capturing return distribution characteristics and the difficulty in extending to multi-dimensional rewards. Theoretically, the algorithm’s convergence is proven, aligning with the interpolative nature of Sinkhorn divergence between Wasserstein distance and Maximum Mean Discrepancy (MMD). Empirically, SinkhornDRL demonstrates superior performance across various Atari games, especially in multi-dimensional reward scenarios. This success stems from the algorithm’s ability to accurately capture return distribution complexities and enhanced stability during training, offering a compelling alternative in the field of distributional reinforcement learning.

Multi-dim. Rewards

#

The extension of distributional reinforcement learning (RL) to handle multi-dimensional rewards is a significant contribution. Standard quantile regression approaches struggle with this extension, often due to computational intractability in high-dimensional spaces. The paper addresses this challenge by leveraging Sinkhorn divergence, a regularized Wasserstein distance, which efficiently approximates optimal transport even in high dimensions. This allows the algorithm to effectively compare multi-dimensional return distributions, unlike methods that rely on pre-specified statistics like quantiles, which are insufficient in capturing the complexity of multi-dimensional data. The theoretical analysis demonstrating the contraction property of the distributional Bellman operator under Sinkhorn divergence for multi-dimensional rewards further validates this approach. Empirically, the proposed method’s success in multi-dimensional reward settings highlights the practical value of this theoretical contribution, showcasing its effectiveness in scenarios beyond the typical one-dimensional reward frameworks.

Convergence Theory

#

A robust convergence theory is crucial for distributional reinforcement learning (RL) algorithms. The paper likely explores the contraction properties of the distributional Bellman operator under different divergence measures, such as Wasserstein distance and its regularized variants (e.g., Sinkhorn divergence). Proofs of contraction are essential to guarantee convergence and the stability of the algorithm, which are likely presented and discussed. The theoretical analysis may analyze how the choice of divergence affects convergence rates and sample complexity. The interpolation properties between different divergences, such as the relationship between Sinkhorn divergence, Wasserstein distance, and Maximum Mean Discrepancy (MMD), are likely investigated. Understanding these relationships helps to explain algorithm behaviors and informs the selection of appropriate divergence measures for specific RL tasks. The impact of regularization, particularly entropic regularization in Sinkhorn divergence, on convergence and stability is also likely a focus. Multi-dimensional reward settings are likely considered, making the convergence analysis more complex. The theoretical results should provide insights into the algorithm’s behavior and performance, potentially guiding the design and selection of more effective distributional RL algorithms.

Atari Experiments

#

In the Atari experiments section, the authors would likely present empirical results demonstrating the performance of their proposed Sinkhorn Distributional Reinforcement Learning (SinkhornDRL) algorithm. This would involve training the algorithm on a subset of the classic Atari 2600 games, a common benchmark in reinforcement learning. Key aspects to look for would be a comparison of SinkhornDRL against existing distributional RL algorithms like QR-DQN and MMD-DQN, using standard metrics such as average human-normalized scores (HNS) over many games and training frames. A focus on multi-dimensional reward settings would highlight a key advantage of SinkhornDRL, showcasing its ability to handle complex reward structures better than other methods that primarily utilize one-dimensional quantile regression. The results would need to demonstrate statistically significant performance gains, preferably showing learning curves with error bars to indicate the reliability of the results. Ablation studies investigating the impact of hyperparameters (such as the number of Sinkhorn iterations or the regularization strength) on performance would be crucial to understanding the algorithm’s behavior. Finally, a discussion of the computational cost of SinkhornDRL compared to baselines would provide a complete picture of its practical efficacy. Overall, the success of this section hinges on robust empirical evidence supporting the claims made by the authors about the algorithm’s improvements.

Future Works

#

The paper’s “Future Works” section suggests several promising avenues for research. Extending Sinkhorn distributional RL by incorporating implicit generative models could significantly improve its performance and efficiency. This involves exploring how to parameterize the cost function within the Sinkhorn divergence framework and increasing the model’s capacity for better approximation of return distributions. Developing new quantitative criteria for choosing the optimal divergence metric in different environments is also critical. The current choice heavily relies on empirical evaluations and lacks a principled approach to guide decision-making. Therefore, developing such a criterion would improve the algorithm’s generalizability and make it more adaptable to various RL tasks. Finally, exploring further applications of Sinkhorn divergence and optimal transport methods within RL is crucial, possibly expanding beyond the scope of distributional RL, such as in model-free RL algorithms. This could involve examining how these techniques can enhance the stability and efficiency of existing methods or even inspire entirely novel RL approaches.

More visual insights

#

More on figures

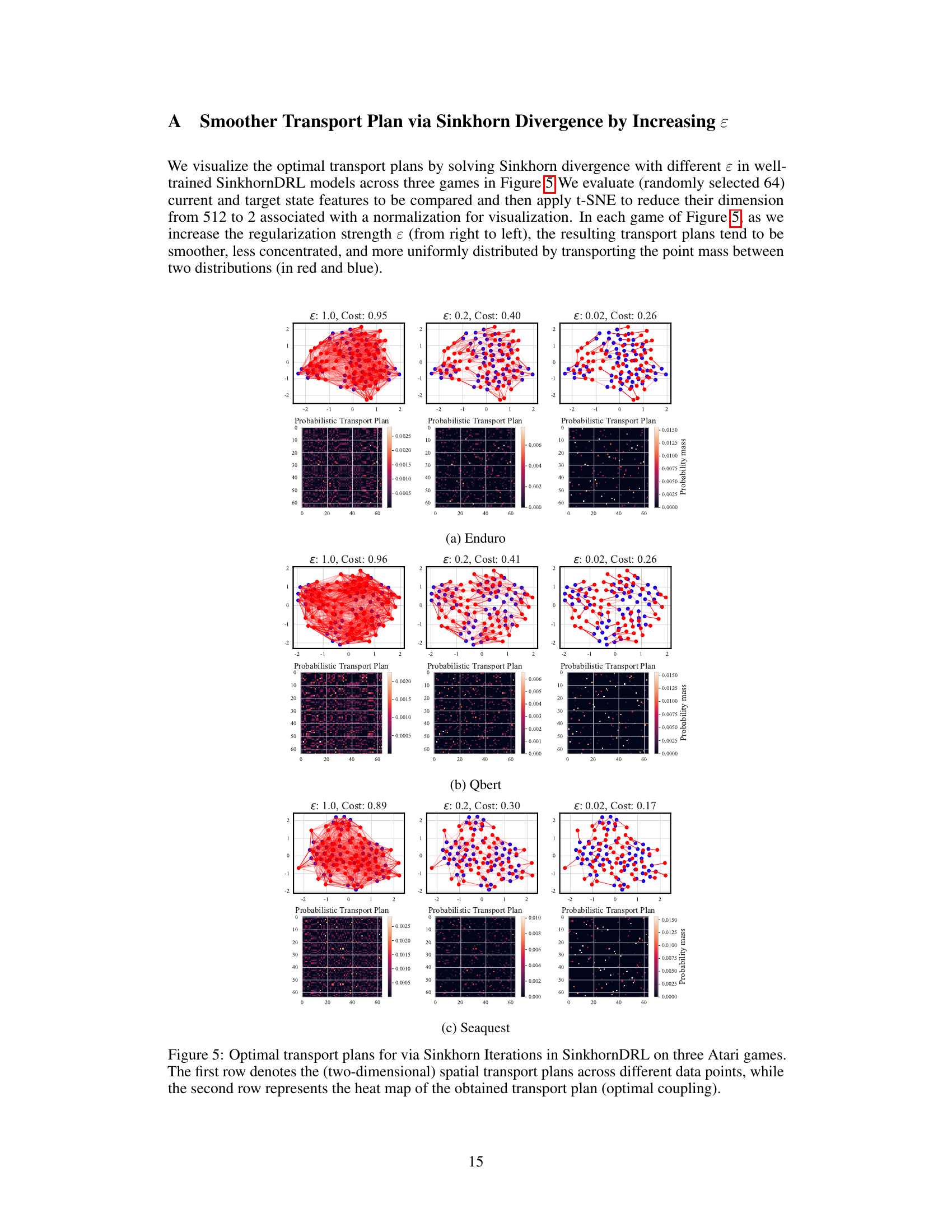
This figure shows the performance improvement of SinkhornDRL compared to QR-DQN and MMD-DQN across 55 Atari games. The ratio improvement is calculated for each game and visualized as a bar chart. Positive values indicate that SinkhornDRL outperformed the respective baseline, while negative values indicate that the baseline performed better. The figure helps to understand which games benefit most from using SinkhornDRL.

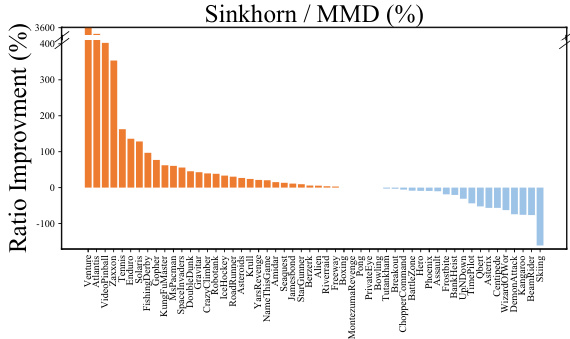
This figure shows the improvement ratio of SinkhornDRL compared to QR-DQN and MMD-DQN across 55 Atari games. The improvement is calculated as the percentage increase in the return of SinkhornDRL over each of the other algorithms, averaged over three separate runs. Positive values indicate that SinkhornDRL performed better; negative values indicate it performed worse. The figure highlights which games benefited most from the use of SinkhornDRL compared to the other algorithms.

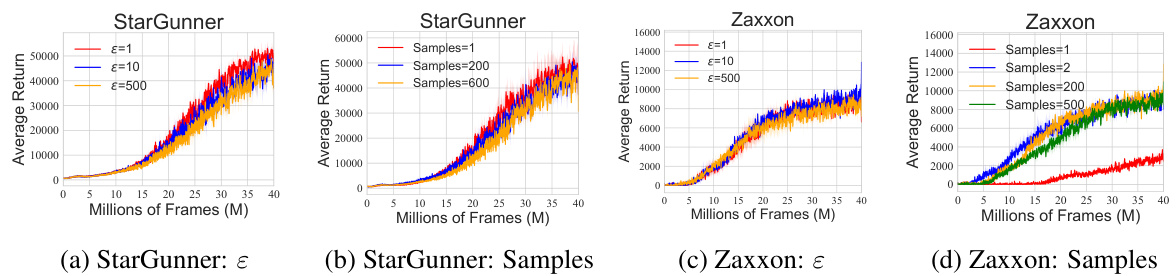
This figure shows the sensitivity analysis of the SinkhornDRL algorithm on two Atari games, Breakout and Seaquest. It illustrates how the algorithm’s performance changes as key hyperparameters are varied: the entropic regularization strength (ε), the number of generated samples (N), and the number of Sinkhorn iterations (L). Learning curves (average return vs. millions of frames) are shown for different values of each hyperparameter, with three independent runs plotted for each configuration to show variability.

This figure compares the performance of SinkhornDRL and MMD-DQN on six Atari games that have been modified to include multiple reward sources. The x-axis represents millions of frames of training, while the y-axis represents average return. Each subplot shows a different game, and each line shows the performance of either SinkhornDRL (red) or MMD-DQN (green). The shaded regions represent standard deviations across multiple runs. The results demonstrate that SinkhornDRL generally outperforms MMD-DQN in these multi-dimensional reward settings.

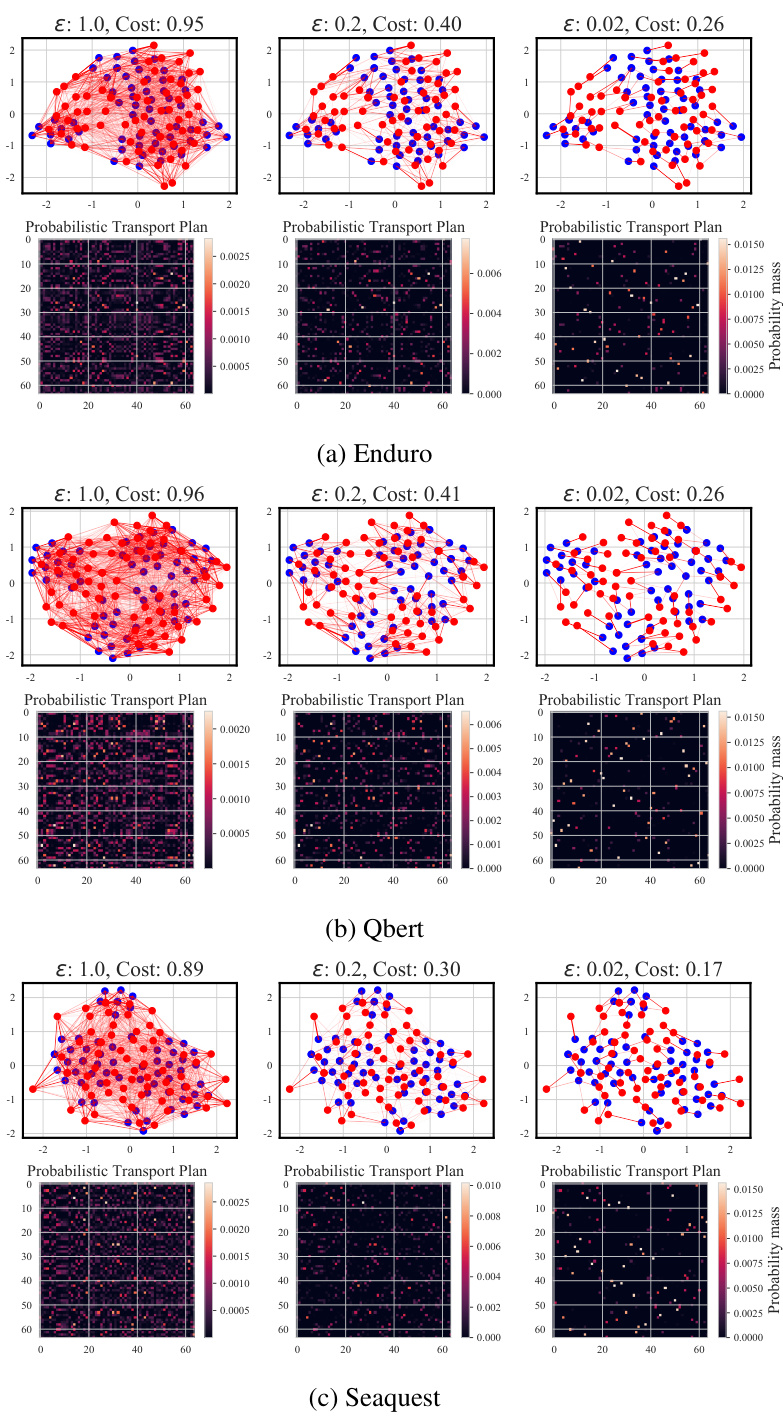
This figure visualizes optimal transport plans obtained using Sinkhorn iterations with varying regularization strengths (epsilon) in three Atari games: Enduro, Qbert, and Seaquest. It demonstrates how increasing epsilon leads to smoother, less concentrated, and more uniformly distributed transport plans, reflecting the effect of regularization on the transport plan.

This figure presents a comparison of the learning curves for three different metrics (Mean, Median, and Interquartile Mean) across various distributional reinforcement learning algorithms. The results are averaged across 55 Atari games and three different seeds (runs) for each algorithm, providing a robust and comprehensive evaluation of algorithm performance. The x-axis represents training time (in millions of frames), while the y-axis displays the Human-Normalized Scores (HNS). This visualization allows for a detailed comparison of the convergence speed and overall performance of each algorithm across different performance metrics.

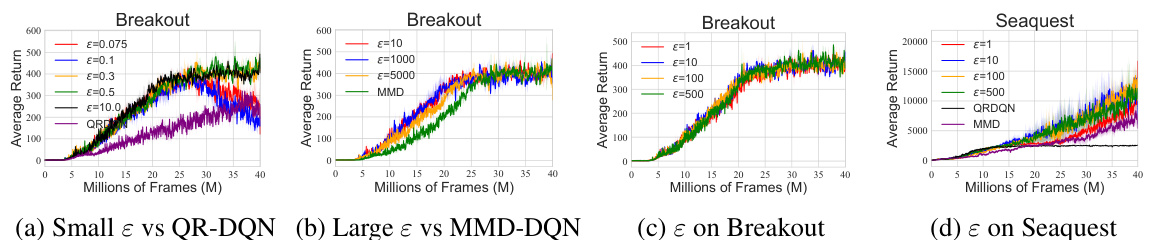
This figure shows the sensitivity analysis of the SinkhornDRL algorithm’s performance with respect to the hyperparameter epsilon (ε). The left two subfigures (a and b) compare the performance of SinkhornDRL against QR-DQN (small ε) and MMD-DQN (large ε) on the Breakout game. The right two subfigures (c and d) show the effect of varying ε on the Breakout and Seaquest games, respectively. The results demonstrate that a well-tuned value for ε is crucial for optimal performance, avoiding numerical instability issues that arise when ε is too small or too large.

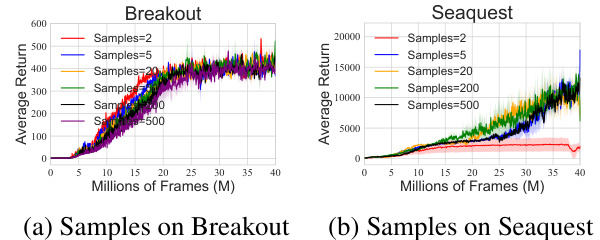
This figure shows the sensitivity analysis of the SinkhornDRL algorithm on two Atari games, Breakout and Seaquest. It explores how different hyperparameters affect the algorithm’s performance. Specifically, it investigates the impact of the regularization parameter (ε), the number of samples used to approximate the distribution (Samples), and the number of Sinkhorn iterations (L). Learning curves, averaged over three seeds, are presented for each hyperparameter setting, visualizing the average return over millions of frames during training.

This figure presents sensitivity analysis of the SinkhornDRL algorithm’s performance with respect to the hyperparameter epsilon (ε). Panels (a) and (b) show comparisons against QR-DQN (small ε) and MMD-DQN (large ε) on the Breakout game. Panels (c) and (d) show the sensitivity of ε on Breakout and Seaquest, respectively. The results highlight the algorithm’s robustness to changes in ε and reveal its interpolation behavior between Wasserstein and MMD distances.

The figure shows the learning curves for three different metrics (Mean, Median, and IQM(5%)) of human-normalized scores (HNS) across 55 Atari games. The curves compare the performance of five different distributional reinforcement learning algorithms (DQN, C51, QR-DQN, MMD-DQN, and SinkhornDRL). Each curve represents the average performance over three separate runs (seeds) of the algorithm. The shading around each curve illustrates the standard deviation between the runs, indicating the variability of the algorithm’s performance. This allows for a visual comparison of the stability and overall performance of the algorithms on the Atari benchmark.

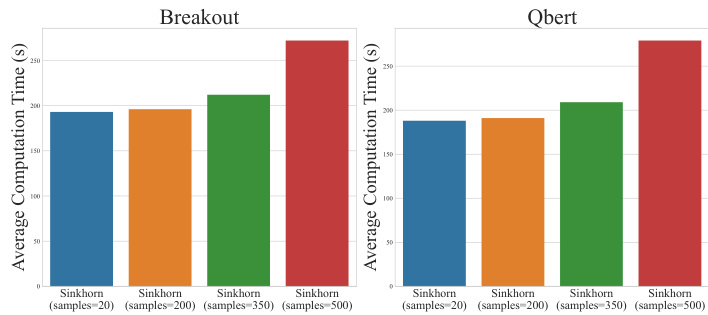
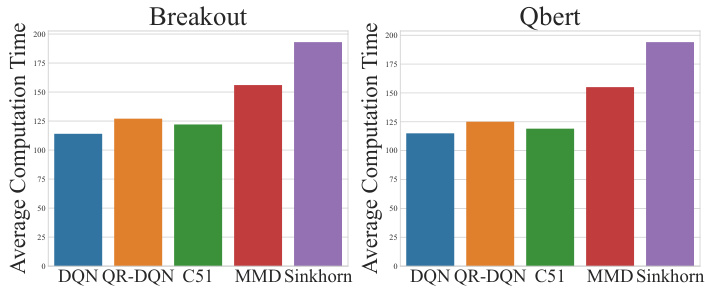
This figure compares the average computational cost per 10,000 iterations for different distributional reinforcement learning (RL) algorithms across two Atari games, Breakout and Qbert. The algorithms compared are DQN, QR-DQN, C51, MMD-DQN, and the proposed SinkhornDRL. For SinkhornDRL, the impact of varying the number of samples (N) is also shown, ranging from 20 to 500. The figure illustrates the relative computational overhead of SinkhornDRL compared to the other algorithms and highlights the effect of the number of samples on its computational cost.

More on tables

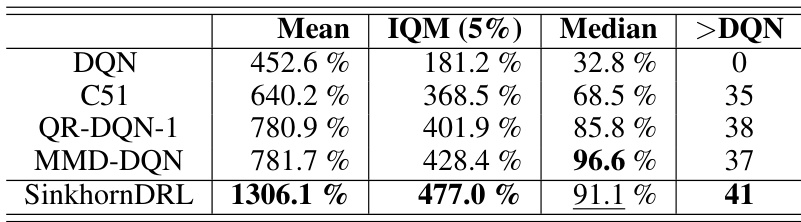
This table presents a comparison of the performance of several distributional reinforcement learning algorithms across 55 Atari games. The algorithms are DQN, C51, QR-DQN, MMD-DQN, and the proposed SinkhornDRL. Performance is measured using three metrics: Mean, Interquartile Mean (IQM) at the 5% level, and Median of the Human Normalized Scores (HNS). The final column, ‘>DQN’, indicates how many games each algorithm outperformed DQN.

This table summarizes the properties of various distribution divergences used in distributional reinforcement learning algorithms. It compares algorithms (C51, QR-DQN, MMD-DQN, and SinkhornDRL) across distribution divergence used, distribution representation, convergence rate of the Bellman operator, and sample complexity of the divergence metric. The table highlights the differences in how these algorithms approach the problem of estimating and utilizing return distributions in reinforcement learning.

This table compares several distributional reinforcement learning algorithms based on different divergence metrics (Cramér, Wasserstein, MMD, and Sinkhorn). It highlights key properties for each algorithm, such as the type of distribution representation used (categorical, quantiles, or samples), the convergence rate of the distributional Bellman operator, and the sample complexity of the divergence metric.

Full paper

#