↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Estimating eigenvectors from noisy data is critical in many machine learning applications, but existing spectral methods suffer from high error rates when the underlying signal matrix has high coherence (i.e., its eigenvectors strongly depend on specific standard basis vectors). This is problematic as many real-world datasets exhibit high coherence. Additionally, these methods often rely on assumptions such as Gaussian noise which are not always met in real-world applications.
This paper introduces a novel method that significantly improves eigenvector estimation by mitigating the issue of high coherence. It leverages a carefully selected subset of the observed matrix entries, effectively filtering out noise. Under mild conditions, the method is provably free from coherence dependence and achieves optimal estimation rates under Gaussian noise. Furthermore, the new method showcases improved performance under non-Gaussian noise, demonstrating robustness in real-world conditions. Importantly, new metric entropy bounds are provided which improve understanding of singular subspaces and yield tighter bounds for the general rank-r case.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on high-dimensional data analysis and matrix estimation. It significantly improves the accuracy of eigenvector estimation, especially in scenarios with high coherence and non-Gaussian noise, opening new avenues for improving algorithms in various applications such as community detection, recommendation systems, and dimensionality reduction. The novel bounds derived for rank-r singular subspaces further contribute to the theoretical understanding of these methods.
Visual Insights#

This figure compares the performance of the proposed Algorithm 1 against the standard spectral method for estimating a rank-one matrix’s eigenvector under different noise distributions (Gaussian, Rademacher, Laplacian) and eigenvector generation schemes (Bernoulli, Haar). The estimation error is measured using the l∞ distance (d∞). The results show that Algorithm 1 consistently outperforms the spectral method, with less sensitivity to the incoherence parameter (μ) represented by ||u*||∞.
In-depth insights#
Eigenvector Estimation#
The paper focuses on eigenvector estimation in low-rank signal-plus-noise matrix models, a crucial problem in data science. Traditional spectral methods rely on the observed matrix’s eigenspace, but their accuracy is hampered by the signal’s coherence. This research introduces a novel coherence-free method, proving its effectiveness through theoretical analysis and simulations. The method cleverly selects a subset of entries in the observed matrix to reduce the influence of noise and achieve optimal estimation rates. A key insight is that the entrywise error is independent of the coherence under Gaussian noise. The paper further extends the method for rank-r matrices, demonstrating its robustness. The work also contributes new metric entropy bounds for low-rank subspaces, tightening existing lower bounds for eigenvector estimation. Overall, this paper offers significant advancements in eigenvector estimation accuracy and theoretical understanding, paving the way for improved data analysis techniques.
Coherence-Free Method#
The concept of a “coherence-free method” in the context of eigenvector estimation is significant because traditional spectral methods often suffer from performance degradation when the underlying signal matrix exhibits high coherence with respect to the standard basis. High coherence implies that the signal is concentrated in a small number of coordinates, which makes the signal vulnerable to noise. A coherence-free method aims to overcome this limitation by developing an algorithm whose accuracy is not affected by the coherence level of the signal matrix. This is achieved by carefully selecting a subset of entries from the noisy observation matrix, focusing on those which are most likely to be dominated by the signal rather than noise. The theoretical guarantees usually accompany such methods, proving that the entrywise estimation error is independent of the coherence under certain assumptions (e.g., Gaussian noise). The practical implications are significant because it allows these methods to be applied effectively to a broader class of problems, even when data exhibits complex and non-random structures. This approach demonstrates significant improvement over traditional methods in both theory and empirical results.
Minimax Lower Bounds#
The minimax lower bound analysis in this research paper is crucial for understanding the fundamental limits of eigenvector estimation. It establishes a benchmark for the performance of any estimation method by providing a lower bound on the achievable error. This framework is particularly valuable in high-dimensional settings where the complexity of the problem scales with the dimensionality of the data. The analysis likely leverages concepts from information theory and statistical decision theory. A key aspect is how the bounds relate to the incoherence parameter of the low-rank signal matrix. Incoherent matrices are easier to estimate, while coherent matrices present greater challenges. Therefore, it is important to examine how minimax lower bounds scale with incoherence. The improved lower bounds derived in the paper suggest that existing methods might not achieve optimal rates, particularly in the case of high coherence and low signal-to-noise ratios. This highlights the need for new algorithms specifically designed to overcome these limitations and achieve the optimal rate in various regimes. The analysis likely involves sophisticated mathematical tools and techniques. Demonstrating the tightness of these bounds using matching upper bounds further strengthens the analysis. This would fully characterize the minimax rate for the specific problem.
Algorithm Performance#
Analyzing algorithm performance requires a multifaceted approach. This involves evaluating not only accuracy, as measured by metrics like the l∞ distance between estimated and true eigenvectors, but also runtime efficiency and scalability. The paper demonstrates improvements in accuracy compared to traditional spectral methods, particularly in high-coherence scenarios where spectral methods underperform. However, a detailed analysis of runtime and scalability across various dataset sizes and ranks is lacking, limiting a full understanding of practical performance. Further investigation could include empirical comparisons with other state-of-the-art algorithms and an examination of memory usage. Moreover, the assumption of known noise variance is a constraint and the proposed algorithm’s robustness to violations of this assumption warrants further exploration. Theoretical guarantees are provided only up to logarithmic factors, suggesting potential for further refinement of the error bounds. Finally, future work should examine the algorithm’s performance with different noise distributions and its sensitivity to varying eigengaps.
Future Research#
The paper’s “Future Research” section would ideally expand on several key limitations. Relaxing the homoscedastic noise assumption is crucial for broader applicability. The current reliance on a technical assumption (Assumption 2) regarding the signal eigenvector’s entry distribution warrants further investigation; a proof that this constraint is not strictly necessary would significantly improve the results. Extending the theoretical analysis to the rank-r Algorithm 2 is a major goal. While simulations suggest robustness, rigorous theoretical bounds are needed. Investigating the suboptimality of the spectral method in the low signal-to-noise regime should be explored, potentially via alternative algorithms like AMP, refining them to handle entrywise error. Finally, a more comprehensive study exploring the interplay between condition number and coherence in eigenvector estimation would be highly valuable.
More visual insights#
More on figures
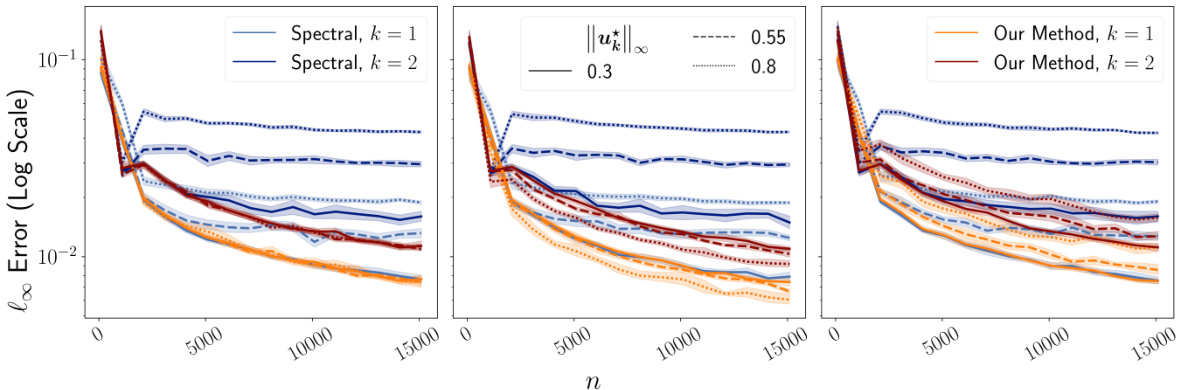
The figure compares the performance of Algorithm 2 against the standard spectral method for estimating eigenvectors of a rank-r matrix. It shows the l∞ error as a function of the matrix dimension (n) for different levels of coherence (represented by ||u*||∞), noise types (Gaussian, Rademacher, Laplacian), and eigenvector indices (k=1,2). Shaded regions represent 95% bootstrap confidence intervals. The plot demonstrates that Algorithm 2 consistently outperforms the spectral method, especially at higher coherence levels, suggesting its robustness and effectiveness across various noise distributions.

The figure compares the performance of Algorithm 1 and the standard spectral method for estimating the leading eigenvector of a rank-one matrix under different noise distributions (Gaussian, Rademacher, Laplacian) and different generation methods for u* (Bernoulli, Haar). The plot shows the l∞ estimation error against the matrix dimension (n) for different values of ||u*||∞. Algorithm 1 consistently outperforms the spectral method, particularly when ||u*||∞ is large, demonstrating its robustness to coherence.
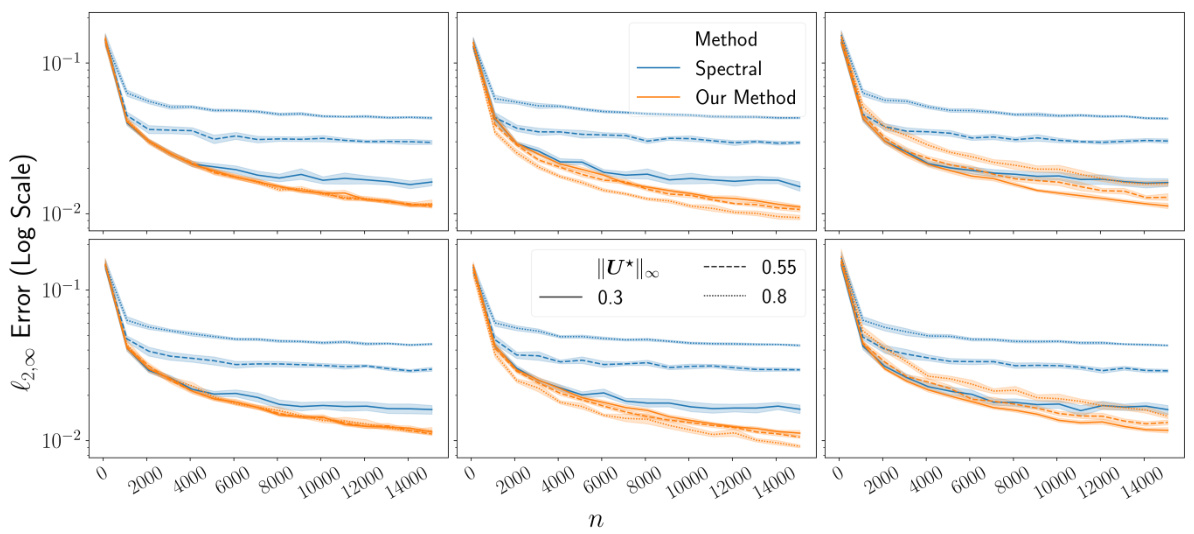
This figure compares the performance of the proposed Algorithm 2 and the standard spectral method in estimating the eigenspace of a rank-2 and rank-3 matrix under different noise distributions and coherence levels (measured by ||U*||∞). The results show that Algorithm 2 consistently outperforms the spectral method, especially at higher coherence levels.
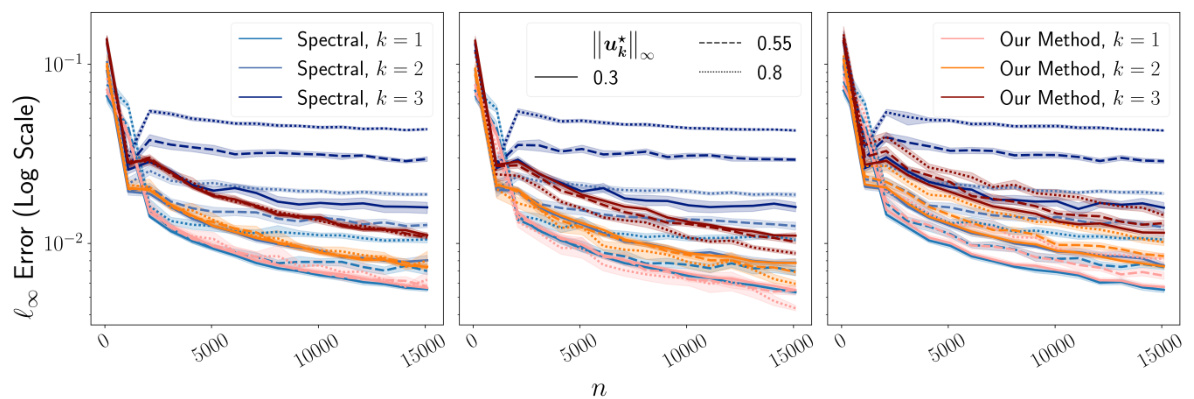
This figure compares the performance of Algorithm 2 and the spectral method in estimating the top three eigenvectors of a rank-3 matrix. The estimation error is measured using the l∞ norm. Different noise distributions (Gaussian, Rademacher, Laplacian) are considered, and the results are shown for three different values of the maximum absolute entry of the true eigenvectors (||u*||∞). Shaded areas represent 95% bootstrap confidence intervals.
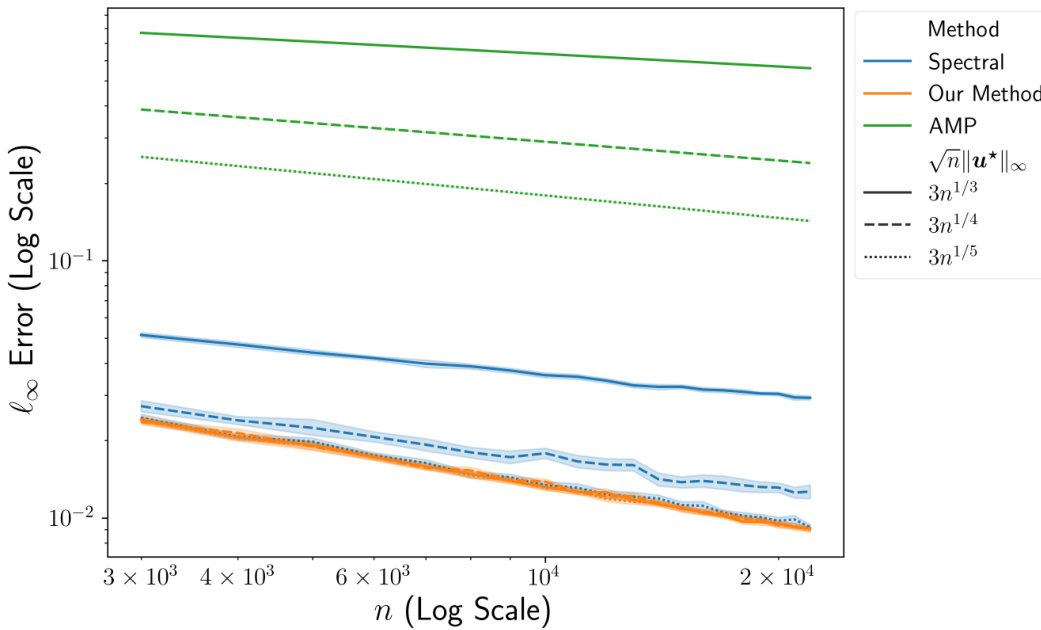
This figure compares the performance of three methods for estimating eigenvectors in a signal-plus-noise model: the spectral method, the approximate message passing (AMP) method, and the proposed method (Algorithm 1). The x-axis represents the dimension n of the matrix, while the y-axis displays the entrywise estimation error (l∞-error). Three different levels of coherence are considered, corresponding to √n||u*||∞ being 3n1/3, 3n1/4, and 3n1/5. The plot reveals that Algorithm 1 significantly outperforms both the spectral and AMP methods, especially for higher values of n and higher coherence. The error rates of Algorithm 1 show almost no dependence on coherence. In contrast, both the spectral method and AMP exhibit stronger dependence on coherence.
Full paper#



















