↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Traditional sparse Principal Component Analysis (PCA) algorithms face challenges with high dimensionality and large effective rank, often requiring computationally expensive procedures. Existing streaming algorithms for sparse PCA either need strong initialization or assume specific covariance structures. This limits their applicability in real-world scenarios where datasets are large and complex, and prior knowledge about the covariance is unavailable. The focus is often on a spiked covariance model, which is a simplified version of the problem.
This research introduces a novel, computationally efficient algorithm for streaming sparse PCA. It leverages Oja’s algorithm, a well-known iterative method, and incorporates a simple thresholding technique to extract sparse principal components. The algorithm is remarkably simple and achieves the minimax error bound under some regularity conditions, using only O(d) space and O(nd) time. The key contribution lies in a novel analysis of Oja’s algorithm’s unnormalized vector, proving that the support can be recovered with high probability in a single pass, paving the way for optimal error rates in high-dimensional settings.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in sparse PCA and high-dimensional data analysis. It addresses the limitations of existing methods by providing a single-pass algorithm achieving minimax optimal error rates with low computational costs. This opens new avenues for handling large-scale datasets and contributes significantly to the growing interest in efficient and scalable sparse PCA techniques.
Visual Insights#

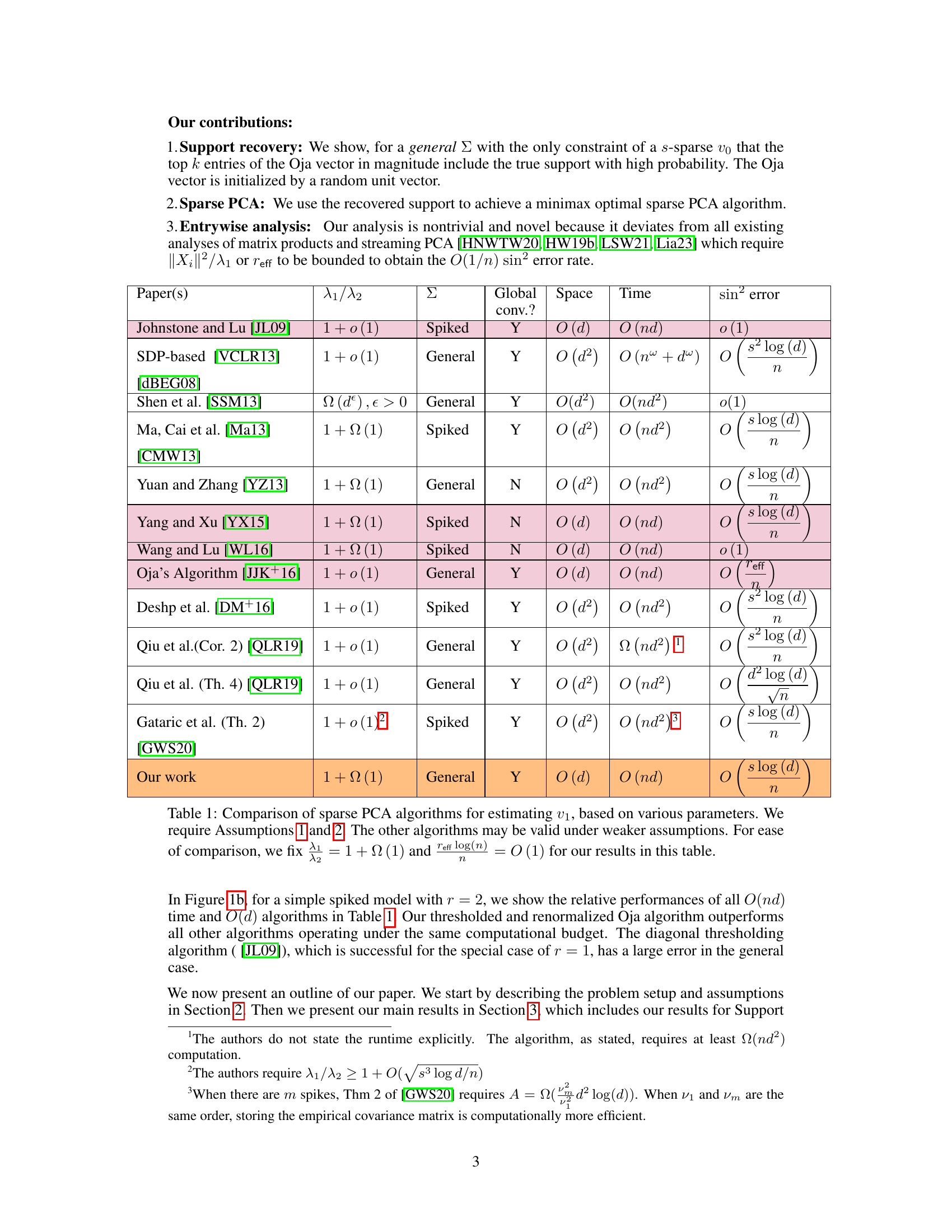
The figure compares four different sparse PCA algorithms. The algorithms operate using O(d) space and O(nd) time. Figure (a) is a graph showing the sin-squared error over timesteps, comparing the proposed algorithm to three existing algorithms. Figure (b) is an image of a sample covariance matrix.
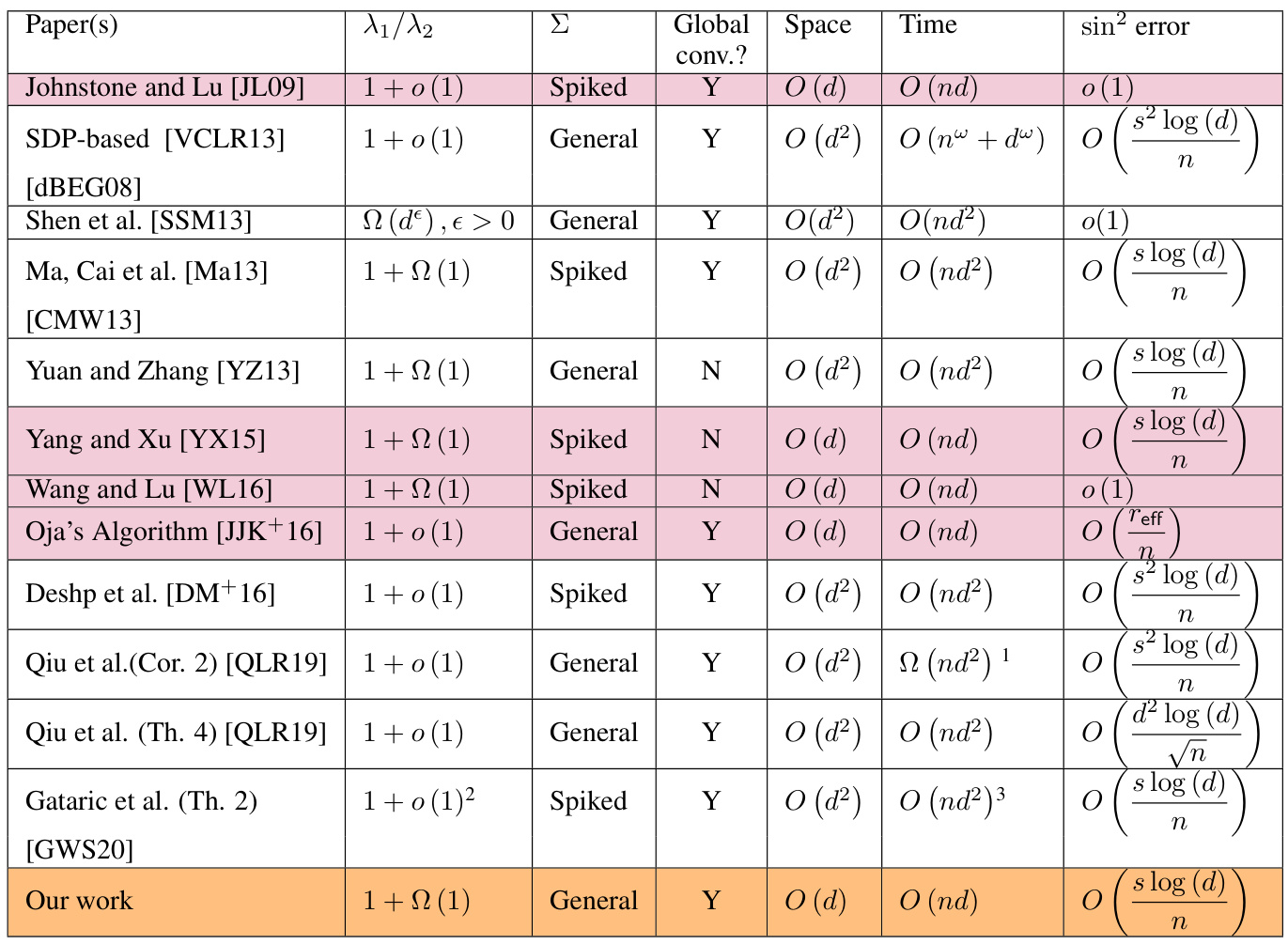
This table compares different sparse PCA algorithms based on several factors: the ratio of the largest to second largest eigenvalues (λ₁/λ₂), whether the algorithm works for general or spiked covariance matrices, whether it converges globally, space and time complexity, and the sin² error achieved. Assumptions 1 and 2 from the paper are required for the proposed algorithm’s performance guarantees, while others may have different requirements.
Full paper#