TL;DR#
Community detection in large networks is a critical task across various fields, but existing methods often lack theoretical guarantees or are computationally expensive. The stochastic block model, while simple, offers an interpretable framework for understanding community structures but requires efficient and reliable methods for its application. Many current embedding techniques, such as node2vec, achieve state-of-the-art performance in practice but lack theoretical justification for their effectiveness.
This paper bridges this gap by providing theoretical guarantees for the node2vec embedding approach. Using a balanced two-block stochastic block model, the authors demonstrate that k-means clustering on the node2vec embeddings yields weakly consistent community recovery. The results extend beyond simple SBMs to more complex models and highlight that the specific sampling parameters in node2vec have minimal impact on the performance for large networks. Empirical studies on both real and simulated data confirm these theoretical findings, comparing node2vec with other common methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in network science and machine learning. It provides strong theoretical guarantees for a widely used network embedding method (node2vec), addressing a significant gap in the field. This opens up new avenues for developing more robust and reliable community detection techniques, impacting various applications from social network analysis to biological networks. The empirical validation further strengthens the findings and showcases the method’s practical applicability.
Visual Insights#
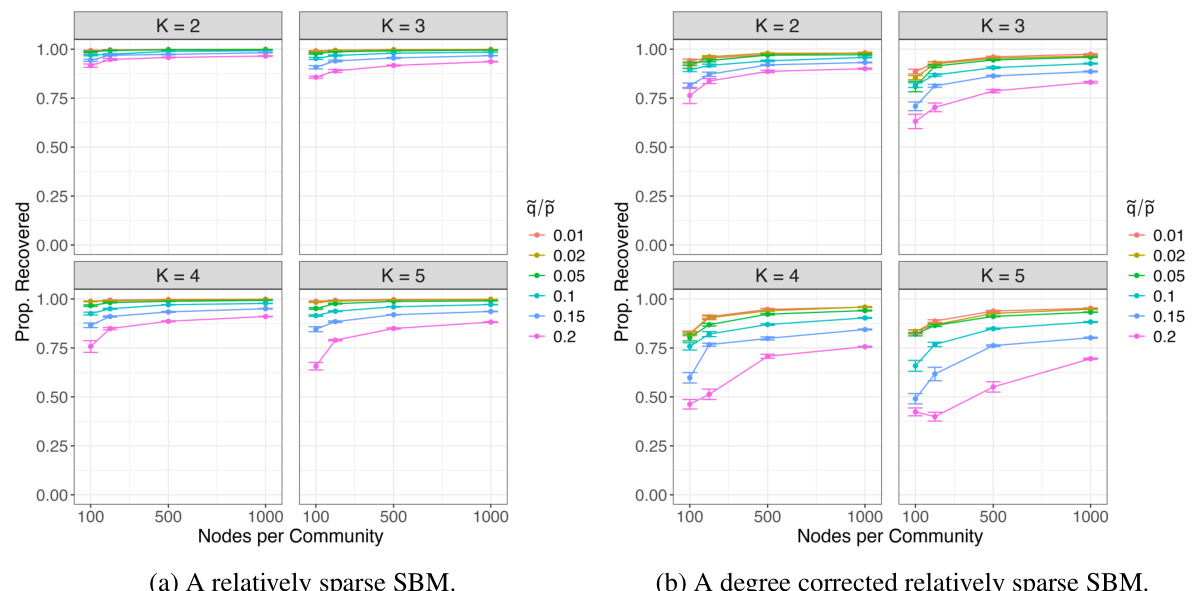
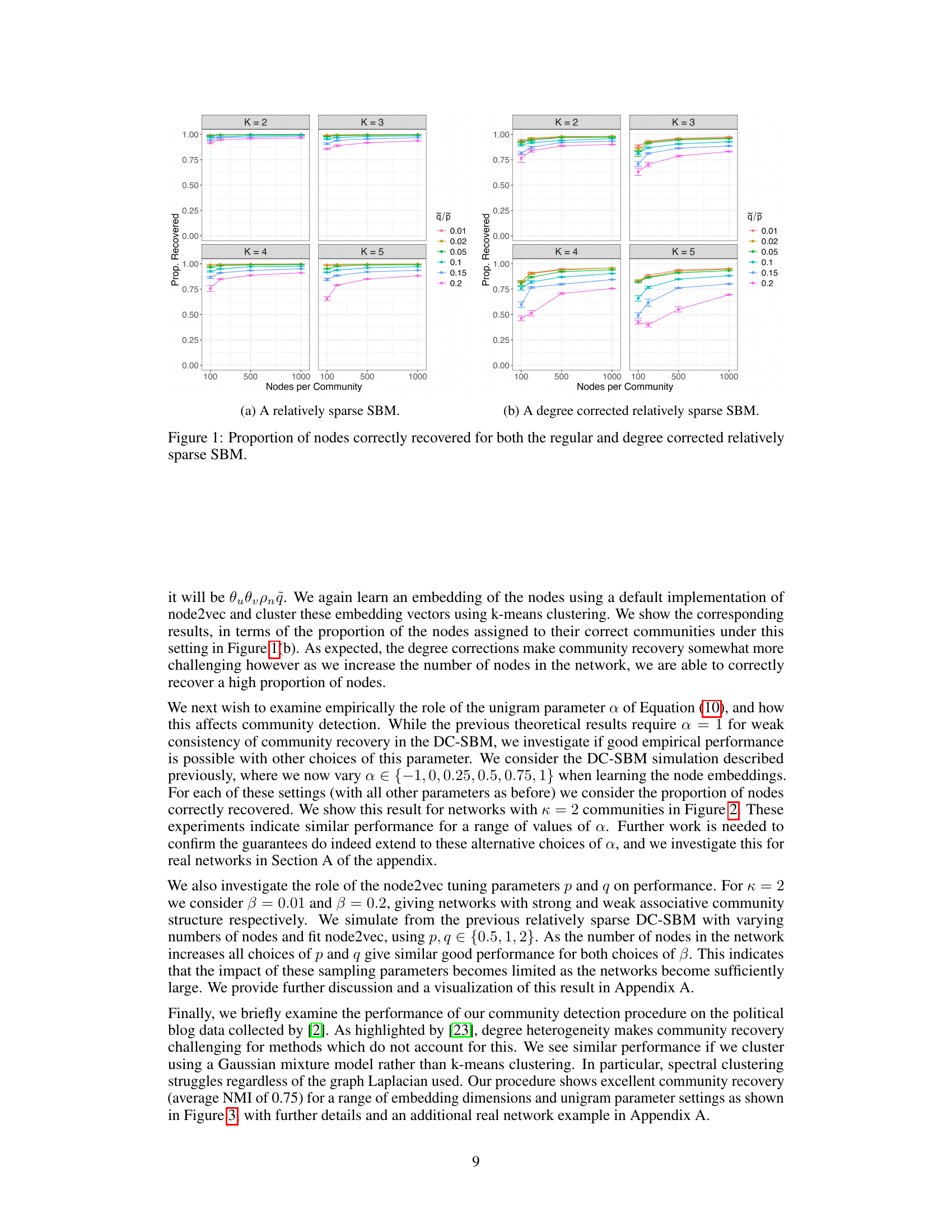
🔼 This figure shows the proportion of nodes correctly classified by k-means clustering of node2vec embeddings for both regular and degree-corrected stochastic block models (SBMs). The x-axis represents the number of nodes per community, while the y-axis shows the proportion of correctly classified nodes. Different lines represent different values of ᾷ/p, which reflects the strength of community structure. The left panel (a) shows results for a relatively sparse SBM, and the right panel (b) shows results for a relatively sparse degree-corrected SBM.
read the caption
Figure 1: Proportion of nodes correctly recovered for both the regular and degree corrected relatively sparse SBM.
In-depth insights#
Node2Vec Limits#
The heading ‘Node2Vec Limits’ prompts a discussion on the constraints and shortcomings of the Node2Vec algorithm for network embedding. A key limitation is its reliance on random walks, which may not fully capture complex network structures or long-range dependencies. The algorithm’s performance can be sensitive to hyperparameter tuning, requiring careful selection of parameters such as walk length, context size, and return and inward parameters for optimal results. Furthermore, Node2Vec’s scalability can be an issue for extremely large graphs due to the computational cost of random walk generation and embedding learning. The theoretical guarantees for community detection using Node2Vec often hold under restrictive assumptions on the network model (e.g., stochastic block models) and may not generalize well to real-world networks with complex community structures and degree heterogeneity. Therefore, while Node2Vec offers a powerful approach to network embedding, it is essential to acknowledge its limitations and consider alternative or complementary techniques for certain applications.
Embedding Power#
The concept of “Embedding Power” in a research paper likely refers to the effectiveness of embedding methods in capturing relevant information from data. A high embedding power means the embeddings successfully encode crucial features, leading to improved performance in downstream tasks such as classification, clustering, or link prediction. Factors influencing embedding power include the choice of embedding algorithm, the dimensionality of the embedding space, and the nature of the data itself. Analyzing embedding power often involves comparing the performance of different embedding techniques on various datasets and evaluating the resulting embeddings’ ability to preserve crucial relationships or patterns. Theoretical analysis might focus on proving bounds on the capacity of embeddings to represent data and the conditions under which optimal results can be achieved. Empirically, embedding power is assessed by measuring the performance improvement in the downstream tasks. A paper exploring embedding power would ideally provide a comprehensive evaluation, including theoretical justifications, empirical evidence, and discussions on the limitations and potential improvements for different embedding methods and data types.
Consistent Recovery#
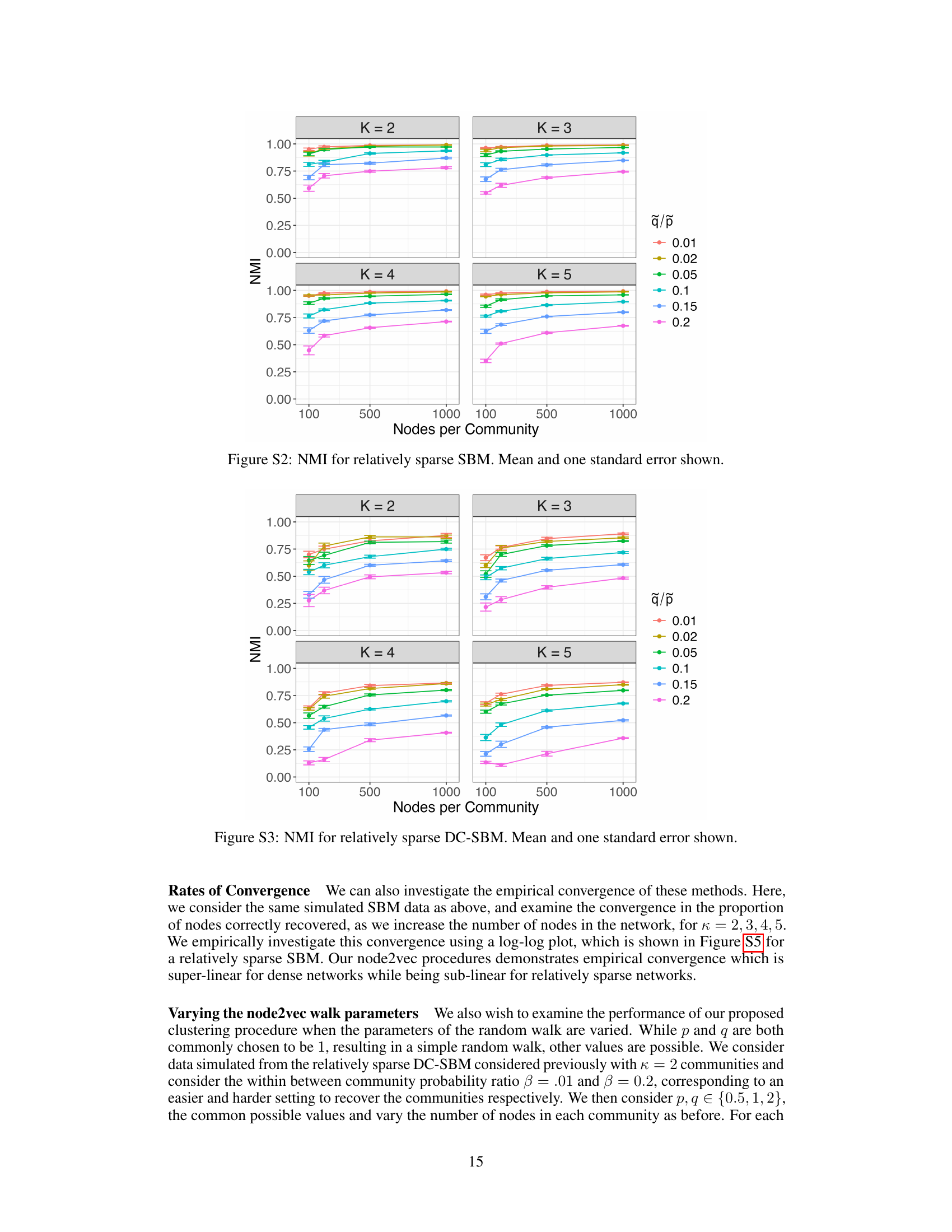
Consistent recovery in community detection signifies the algorithm’s ability to correctly identify community memberships as the network size grows. A crucial aspect is the algorithm’s resilience to noise and variations in network structure. The paper likely explores theoretical guarantees, proving that under specific conditions (e.g., model assumptions, sparsity levels), the method achieves consistent recovery with high probability. Empirical evaluations demonstrate the algorithm’s performance on both simulated and real-world networks to validate theoretical findings. Key factors influencing consistent recovery are likely to include network density, community structure, and hyperparameters. The in-depth analysis might encompass the rate of convergence, comparing the method’s performance against other approaches, and exploring the influence of network structure. Understanding the conditions under which the algorithm guarantees consistent recovery provides valuable insights into its strengths and limitations. The discussion of consistent recovery likely highlights the algorithm’s robustness and efficiency in handling large-scale network data for practical applications.
Future Directions#
The paper’s “Future Directions” section would ideally explore extending the theoretical guarantees to encompass a wider array of node2vec hyperparameters, thereby enhancing the model’s applicability. Improving the consistency of community detection results to achieve stronger guarantees is crucial. Investigating the challenges of estimating the number of communities (K) using node2vec embeddings would be valuable. The study could also benefit from applying these techniques to more complex and recent network embedding methods. Addressing the sparse network regime more thoroughly is needed, perhaps by generalizing the theoretical understanding to less restrictive sparsity conditions. Finally, the impact of sampling parameters in node2vec needs further investigation, especially regarding their behavior as networks scale, to optimize performance and robustness. Empirical evaluation on diverse datasets is essential to strengthen the results and to enhance the overall applicability of the proposed methodology.
Theoretical Bounds#
A theoretical bounds section in a research paper would rigorously establish the limits of a model’s performance or the capabilities of an algorithm. It would likely involve mathematical proofs and derivations, establishing guarantees on the accuracy or convergence under specific assumptions. The strength of such bounds hinges heavily on the realism of those assumptions; overly restrictive assumptions can yield strong bounds but limit applicability, while more relaxed assumptions lead to weaker but potentially more useful bounds. The analysis might cover aspects such as sample complexity, runtime, or error rates, ultimately providing a deeper understanding of the model’s behavior beyond empirical observation. A key insight from such a section would be the identification of crucial parameters that dictate the model’s performance, guiding future improvements and highlighting potential limitations.
More visual insights#
More on figures

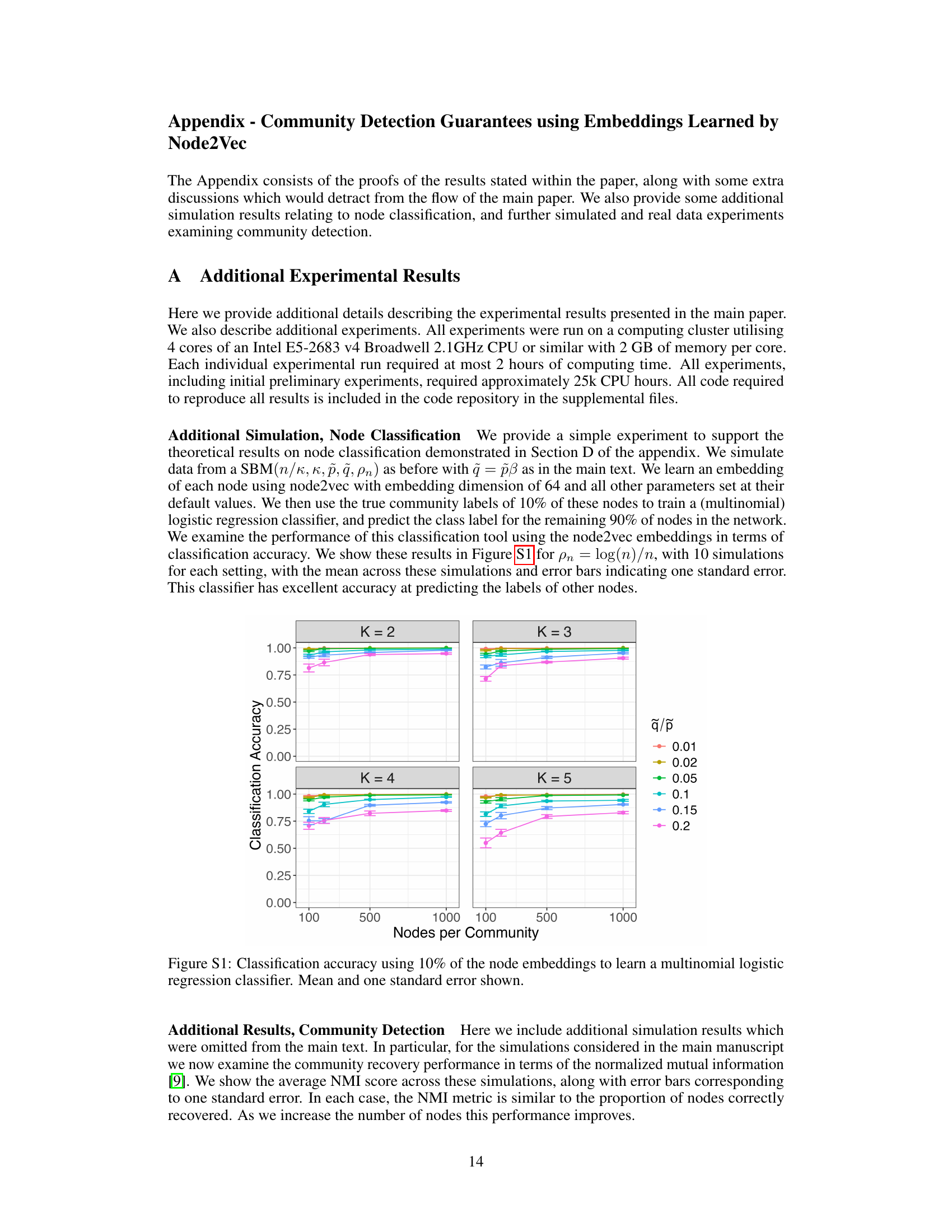
🔼 The figure displays the results of an experiment on the effect of the negative sampling parameter α on the performance of node2vec in community detection. The x-axis represents the number of nodes per community, and the y-axis represents the proportion of nodes correctly classified by the algorithm. Each line corresponds to a different value of the ratio q/p, a hyperparameter in node2vec that controls the balance between returning to previously visited nodes and moving to new nodes in random walks. The error bars show the standard error of the mean across multiple simulations for each setting. The results suggest that the performance of node2vec in community detection is relatively insensitive to the choice of α across the range tested.
read the caption
Figure 2: Proportion of nodes correctly recovered as we vary the negative sampling parameter in node2vec with mean and one standard error for each setting. We see similar performance for each choice of α.
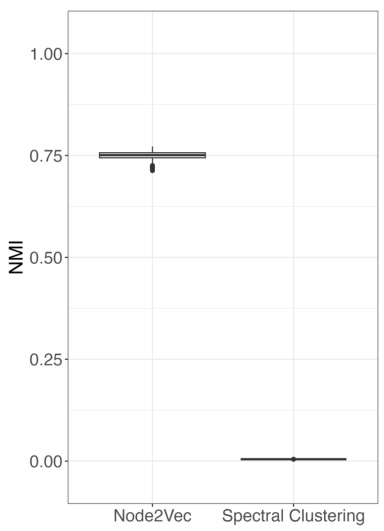
🔼 This figure compares the performance of node2vec with k-means clustering against spectral clustering for community detection on the political blogs dataset. The y-axis represents the Normalized Mutual Information (NMI) score, a measure of the similarity between the predicted and true community assignments. The x-axis shows the two methods used. The box plot for node2vec shows a high NMI score, indicating good community recovery. In contrast, the spectral clustering method shows a very low NMI score, indicating poor performance. This demonstrates the effectiveness of the node2vec embedding method for community detection in this dataset.
read the caption
Figure 3: Node2vec with k-means clustering can recover the communities in the political blog data while spectral clustering fails.

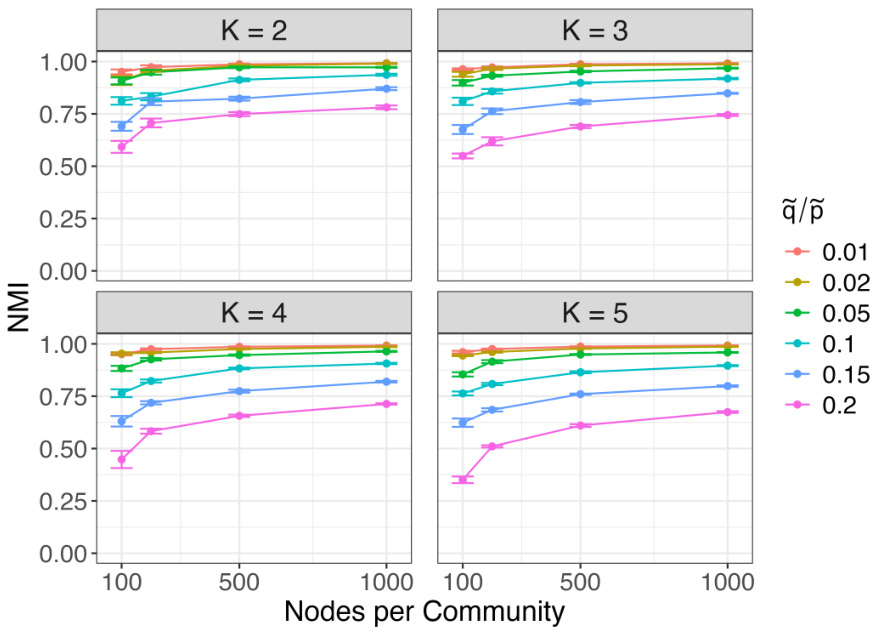
🔼 This figure shows the results of node recovery using k-means clustering on node embeddings learned by node2vec for both stochastic block models (SBM) and degree-corrected stochastic block models (DCSBM). The x-axis represents the number of nodes per community, and the y-axis represents the proportion of nodes correctly classified. Different lines represent different values of q/p, where p is the probability of an edge between nodes in the same community and q is the probability of an edge between nodes in different communities. The left panel (a) shows the results for the regular SBM, and the right panel (b) shows the results for the DCSBM. In both cases, the proportion of correctly classified nodes increases with the number of nodes per community and decreases with the value of q/p, indicating that stronger community structures (smaller q/p) lead to better node recovery.
read the caption
Figure 1: Proportion of nodes correctly recovered for both the regular and degree corrected relatively sparse SBM.
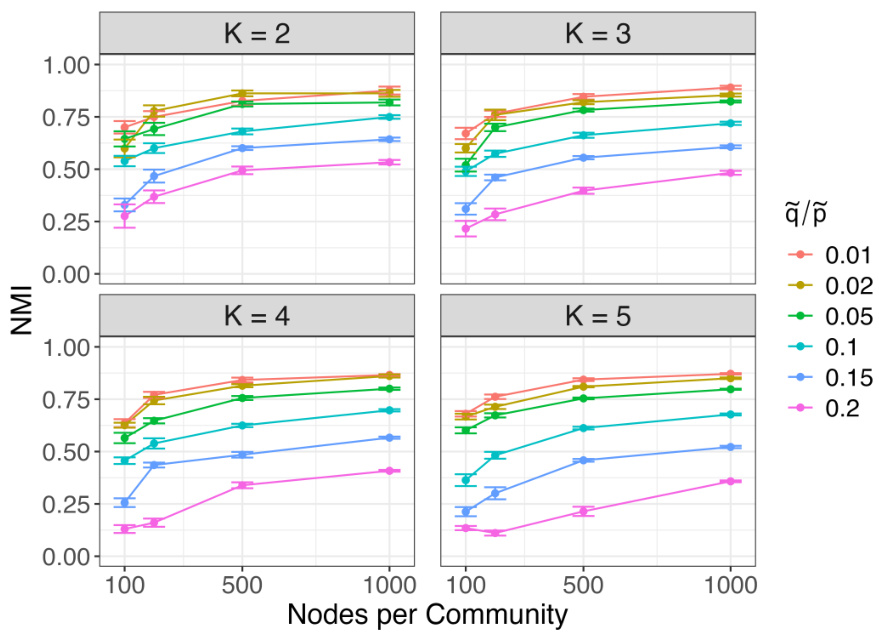
🔼 This figure shows the performance of k-means clustering of node2vec embeddings for community detection in stochastic block models (SBM). Two variations of the SBM are considered: regular and degree-corrected. The x-axis represents the number of nodes per community, and the y-axis represents the proportion of nodes correctly classified. Separate plots are shown for different numbers of communities (K=2, 3, 4, 5). Within each plot, different lines represent different values of q/p, where p and q are parameters controlling the probability of edges in the SBM and influence the network structure. The degree-corrected SBM adds a degree correction factor to account for the heterogeneity of node degrees, which makes community detection more challenging.
read the caption
Figure 1: Proportion of nodes correctly recovered for both the regular and degree corrected relatively sparse SBM.
🔼 This figure shows the performance of the k-means clustering algorithm on node embeddings learned by node2vec for community detection in stochastic block models (SBM) and degree-corrected stochastic block models (DCSBM). The x-axis represents the number of nodes per community, and the y-axis represents the proportion of nodes correctly assigned to their communities. Different lines represent different values of q/p, where p is the probability of connection between nodes in the same community, and q is the probability of connection between nodes in different communities. The figure shows that the performance of node2vec for community detection improves as the number of nodes per community increases and that the performance is better when q/p is smaller, indicating stronger community structure.
read the caption
Figure 1: Proportion of nodes correctly recovered for both the regular and degree corrected relatively sparse SBM.
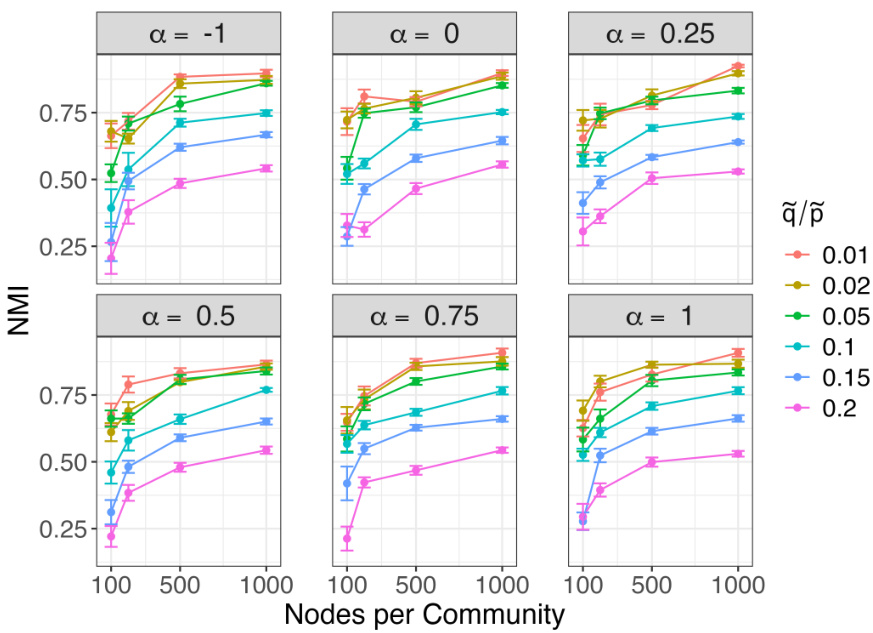
🔼 The figure shows the performance of community detection using node2vec when the negative sampling parameter α is varied. The x-axis represents the number of nodes per community, while the y-axis represents the proportion of nodes correctly classified. Different lines correspond to different values of q/p (the ratio between the probabilities of returning to previously visited nodes and exploring new nodes). The results show that the performance of community detection using node2vec is relatively stable across a range of values for α, suggesting that this hyperparameter may not be critically important.
read the caption
Figure 2: Proportion of nodes correctly recovered as we vary the negative sampling parameter in node2vec with mean and one standard error for each setting. We see similar performance for each choice of α.
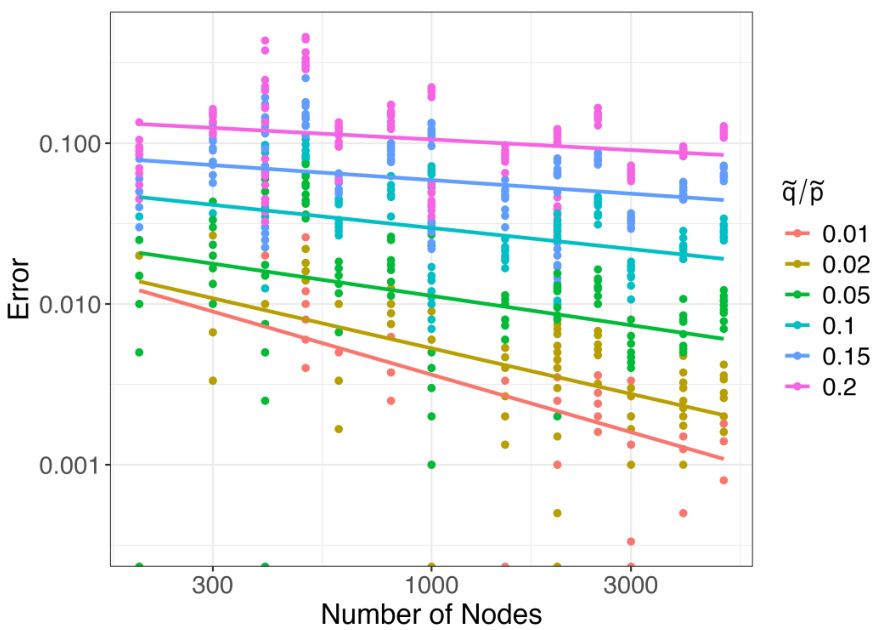
🔼 This figure shows the results of simulation studies using stochastic block models (SBM) and degree-corrected stochastic block models (DCSBM). The proportion of correctly classified nodes is plotted against the number of nodes per community for different values of the ratio between within and between community edge probabilities (q/p). The results show that the proportion of correctly classified nodes increases as the number of nodes increases, and that the performance is better for smaller values of q/p (stronger community structure). The degree correction makes community recovery somewhat more challenging but this effect decreases as the network size increases.
read the caption
Figure 1: Proportion of nodes correctly recovered for both the regular and degree corrected relatively sparse SBM.

🔼 This figure shows the results of experiments using simulated data from stochastic block models (SBM) and degree-corrected stochastic block models (DCSBM). The proportion of nodes correctly classified using k-means clustering on node2vec embeddings is shown for various numbers of nodes per community and different values of β (the ratio of between-community to within-community edge probabilities). The left panel (a) shows results for the standard SBM, while the right panel (b) shows results for the DCSBM. The results demonstrate good community recovery, especially in the denser network settings with a smaller β.
read the caption
Figure 1: Proportion of nodes correctly recovered for both the regular and degree corrected relatively sparse SBM.
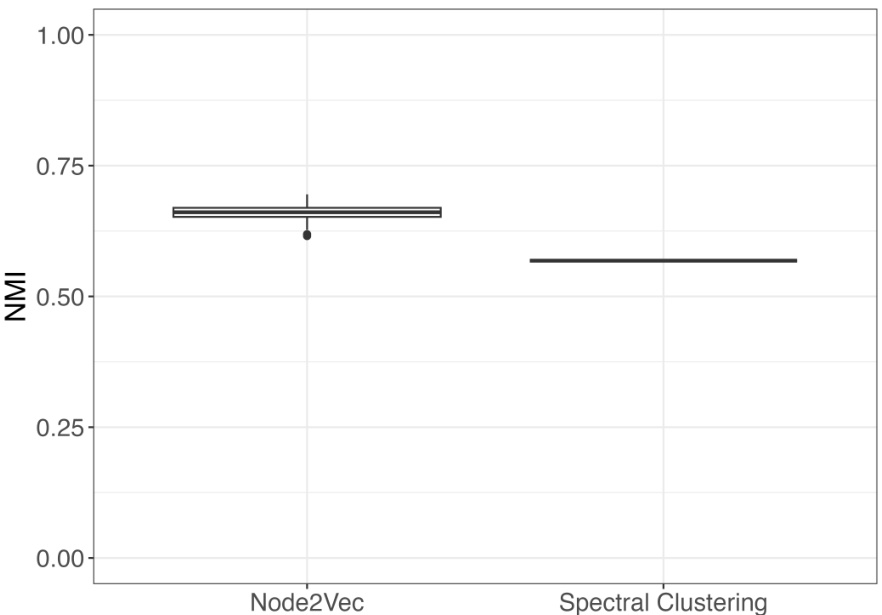
🔼 This figure compares the performance of node2vec with k-means clustering and spectral clustering in recovering communities from the political blog dataset. The boxplots visually represent the distribution of the Normalized Mutual Information (NMI) scores across multiple simulations for each method. The results show that node2vec achieves significantly higher NMI scores, indicating better community recovery compared to spectral clustering. The superior performance of node2vec highlights its effectiveness in handling the complexities of real-world network data for community detection.
read the caption
Figure 3: Node2vec with k-means clustering can recover the communities in the political blog data while spectral clustering fails.

🔼 This figure compares the performance of node2vec with k-means clustering and spectral clustering on the political blog dataset. The results show that node2vec achieves significantly better community recovery (higher NMI score) than spectral clustering, demonstrating the effectiveness of node2vec for community detection in this specific dataset. The poor performance of spectral clustering highlights its limitations when dealing with degree heterogeneity in real-world networks.
read the caption
Figure 3: Node2vec with k-means clustering can recover the communities in the political blog data while spectral clustering fails.
🔼 This figure compares the performance of node2vec with k-means clustering and spectral clustering on the political blog dataset. The results show that node2vec with k-means clustering achieves a significantly higher normalized mutual information (NMI) score, indicating better community detection accuracy than spectral clustering which fails to recover the community structure effectively. This highlights the effectiveness of the node2vec embedding approach for community detection, especially in networks with complex community structures.
read the caption
Figure 3: Node2vec with k-means clustering can recover the communities in the political blog data while spectral clustering fails.
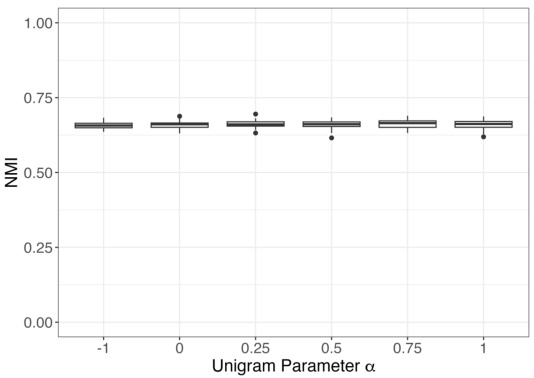
🔼 This figure shows the result of varying the negative sampling parameter α in node2vec for a relatively sparse degree corrected stochastic block model with two communities. The x-axis shows the ratio of between-community to within-community edge probabilities (β), and the y-axis shows the proportion of nodes correctly classified by k-means clustering of the node2vec embeddings. For each β value, multiple simulations with varying numbers of nodes per community are shown, with mean and standard error displayed. The results show consistent performance across different values of α, suggesting this parameter is relatively robust in the sparse setting, at least for balanced two community models.
read the caption
Figure 2: Proportion of nodes correctly recovered as we vary the negative sampling parameter in node2vec with mean and one standard error for each setting. We see similar performance for each choice of α.
Full paper#