↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
The classic Entropic Optimal Transport (EOT) method suffers from sensitivity to outliers and imbalanced data, leading to inaccurate results. Existing solutions often rely on complex heuristics or computationally expensive neural networks. This necessitates the development of robust and efficient solvers for unbalanced EOT (UEOT).
This paper presents a novel UEOT solver, named LightUnbalancedOptimalTransport. The method uses a unique non-minimax optimization objective, combined with a light parametrization technique, making it both computationally efficient and theoretically grounded. The authors demonstrate the solver’s efficacy through extensive experiments and provide generalization bounds to validate its accuracy and performance on various tasks, showing improvements over existing methods.
Key Takeaways#
Why does it matter?#
This paper is important because it offers a novel, lightweight solution to a persistent problem in optimal transport: handling unbalanced data. It’s theoretically sound, provides fast computation, and offers generalization bounds, making it a valuable contribution for researchers working with large-scale datasets and complex distributions where traditional methods struggle. This work opens avenues for improving other generative models and applications relying on optimal transport.
Visual Insights#
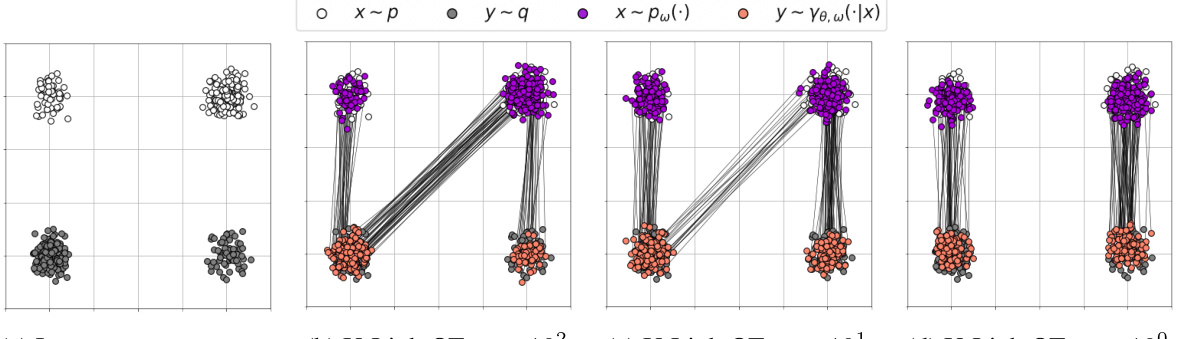
This figure visualizes the conditional plans learned by the U-LightOT solver for a Gaussian Mixture experiment with different levels of unbalancedness (τ). The unbalancedness parameter, τ, controls the level of mass imbalance allowed between the source and target distributions. The plots show how the learned transport plan (γθ,ω(y|x)) changes as τ varies from 10^0 to 10^2. The normalized marginal (pɛ) of the transport plan is also shown for comparison.
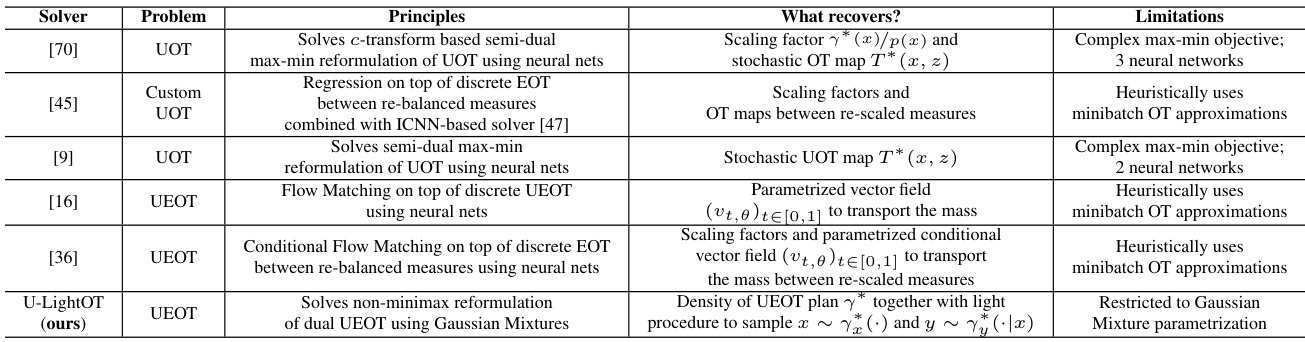
This table compares different solvers for Unbalanced Optimal Transport (UOT) and Unbalanced Entropic Optimal Transport (UEOT) problems. For each solver, it lists the principles used, what the solver recovers (e.g., scaling factors, optimal transport maps), and its limitations. The table highlights the differences in approaches, such as using neural networks versus a Gaussian Mixture parametrization, and the trade-offs between computational complexity and theoretical justification.
In-depth insights#
UEOT Optimization#
Unbalanced Entropic Optimal Transport (UEOT) optimization tackles the limitations of classic optimal transport by relaxing marginal constraints, allowing for mass variations and increased robustness to outliers and class imbalances. This is crucial in many machine learning applications where data is often noisy or suffers from skewed distributions. Efficient solvers for UEOT are essential for practical applicability, and research focuses on developing theoretically grounded, computationally lightweight algorithms that can achieve accurate approximations of UEOT solutions. Novel optimization objectives and parametrizations (like Gaussian mixtures) are explored to improve speed and efficiency while ensuring theoretical guarantees, such as generalization bounds. The effectiveness of these methods often hinges on balancing computational tractability with the accuracy of the approximation. There is ongoing exploration into the trade-offs between computational cost, theoretical guarantees and the suitability of these techniques for various applications and data modalities.
Gaussian Mixture#
The application of Gaussian Mixture Models (GMMs) in the context of optimal transport is a powerful technique. GMMs offer a flexible way to approximate probability distributions, which is crucial when dealing with continuous optimal transport problems where the true distributions might be unknown or complex. By representing the transport plan (the coupling of the source and target distributions) as a mixture of Gaussians, the model’s parameters can be learned efficiently through optimization. This approach effectively avoids the need for computationally expensive procedures often associated with finding the exact solution of continuous optimal transport. Furthermore, the interpretability of GMMs can also shed light on the structure of the optimal transport map. The parameters of the Gaussian components provide insights into the relationship between the source and target distributions, showing how probability mass is shifted and transformed between the two spaces. The Gaussian Mixture parametrization has both theoretical and practical advantages. Theoretically, it allows for the derivation of generalization bounds and proves the universal approximation property of the resulting solver. Practically, this choice of parametrization also simplifies the computational burden, allowing for faster and more efficient solving of the optimal transport problem. In summary, employing GMMs in optimal transport is a significant advancement. It combines the strengths of GMMs for approximation and the power of optimal transport for solving various tasks related to probability distribution manipulation.
Generalization Bounds#
The section on ‘Generalization Bounds’ in a machine learning research paper is crucial for establishing the reliability and applicability of a model beyond the training data. It rigorously examines how well a model’s performance on unseen data generalizes from its performance on the training data. Tight generalization bounds are highly desirable, indicating strong predictive capabilities. The analysis often involves techniques from statistical learning theory, such as Rademacher complexity or VC dimension, to quantify the model’s capacity and its potential for overfitting. The derived bounds usually depend on factors like the model’s complexity, the size of the training dataset, and the properties of the data distribution. A successful demonstration of strong generalization capabilities significantly enhances the paper’s credibility, proving the model’s practical value and robustness. Conversely, loose or weak bounds raise concerns about overfitting and limited applicability to real-world scenarios, emphasizing the need for further investigation or improvements to the model’s design or training process.
Image Translation#
The concept of ‘Image Translation’ within the context of optimal transport is fascinating. It leverages the mathematical framework of optimal transport to map images from one domain to another, achieving transformations that preserve structural information. The core idea is to learn a mapping (a transport plan) that minimizes a cost function, often reflecting the distance between corresponding image features. This is particularly useful in unpaired image-to-image translation where direct pixel correspondences are unavailable, allowing for style transfer or object manipulation across different image sets. The efficiency and theoretical justification of such methods are paramount, and the utilization of techniques like Gaussian mixtures and entropy regularization can lead to significant advancements in this field. Challenges include handling class imbalances and outliers, often mitigated by unbalanced optimal transport (UEOT) approaches. The success of UEOT-based image translation hinges on the ability to learn a mapping that adapts to mass variations, making it a very active and exciting research area. Overall, this research pushes the boundaries of what’s possible in image manipulation, with applications ranging from style transfer and generation to biological data analysis.
Future Work#
Future research directions stemming from this work could explore several promising avenues. Extending the Gaussian Mixture Parametrization: The current model’s reliance on Gaussian mixtures limits its expressiveness; investigating alternative, more flexible parametrizations, perhaps neural networks, could significantly improve its capacity to handle complex data distributions. Improving Generalization Bounds: Tightening the established generalization error bounds would strengthen the theoretical foundation of the algorithm. This could involve refining the analysis techniques or exploring alternative regularization strategies. Addressing High-Dimensional Data: The current implementation focuses on moderately sized datasets. Adapting the methodology for high-dimensional data, common in many applications such as image processing and NLP, is crucial. Investigating other f-Divergences: The use of alternative f-divergences beyond the Kullback-Leibler divergence and Chi-squared could further broaden the solver’s applicability, offering the possibility of fine-tuning the model for specific data characteristics and task requirements. Exploring Unbalanced OT beyond EOT: The current study primarily deals with entropic optimal transport. Extending this framework to incorporate other forms of unbalanced optimal transport that don’t rely on entropy regularization, would expand the algorithm’s versatility and potential impact.
More visual insights#
More on figures
This figure visualizes the conditional plans learned by the U-LightOT solver in a Gaussian Mixture experiment, showing how the unbalancedness parameter τ affects the transport plan. Three different values of τ (1, 10, and 100) are shown, demonstrating how the learned plan changes as the unbalancedness increases. The normalized first marginal, pω, is also displayed.

This figure shows the conditional plans learned by the U-LightOT solver in a Gaussian Mixture experiment for different values of the unbalancedness parameter τ. It illustrates how the parameter τ affects the mass transport from source to target distributions, showing the effect of the unbalancedness on the generated transport plan. The normalized first marginal uw is denoted as pɛ.

This figure shows the conditional plans learned by the U-LightOT solver using scaled χ2-divergences in a Gaussian Mixture experiment. Different subfigures represent different values of the unbalancedness parameter τ (τ ∈ [1, 2, 5, 10]). Each subfigure visualizes the learned conditional probability distribution γθω(y|x), illustrating how the model’s learned transport plan varies as the unbalancedness parameter changes.

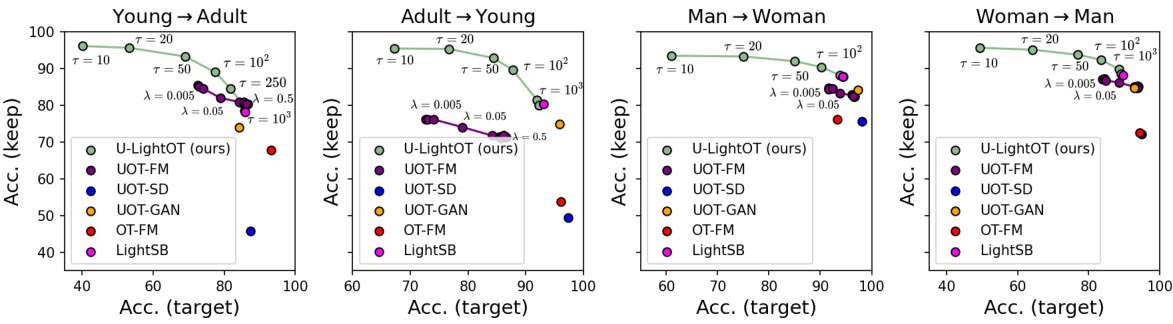
This figure compares the performance of the U-LightOT solver against other OT/EOT methods on image translation tasks. It visualizes the trade-off between ‘keeping’ the original characteristics of the source images and accurately ‘mapping’ them to the target domain. Different unbalancedness parameters (τ for U-LightOT, λ for UOT-FM) are shown, illustrating how this parameter affects the accuracy of both aspects. The plots demonstrate that U-LightOT achieves a better balance compared to several baselines, excelling in preserving source image attributes.
This figure shows the conditional plans (probability distributions over y given x) learned by the U-LightOT solver for different values of the unbalancedness parameter (τ). The experiment uses Gaussian Mixture data. The parameter τ controls the balance between the marginal distributions of source and target measures; a smaller τ indicates a more balanced situation, while larger τ values show an increased imbalance. Note that pε is a normalized version of the learned marginal distribution.
More on tables
This table compares different existing solvers for unbalanced optimal transport (UOT) and unbalanced entropic optimal transport (UEOT) problems with the proposed U-LightOT solver. For each solver, the table lists the problem it solves (UOT or UEOT), the principles behind its construction, what it recovers (e.g., scaling factors, optimal transport maps), and its limitations. The table highlights the U-LightOT solver as a novel, theoretically justified, lightweight alternative to existing methods.

This table compares different unbalanced optimal transport (UOT) and unbalanced entropic optimal transport (UEOT) solvers. It contrasts their core principles (how they solve the problem), the type of problem they address (UOT or UEOT), the solver type, what aspect of the OT plan they recover (e.g., stochastic OT map, scaling factors), and any limitations of the approaches.

This table compares different existing unbalanced optimal transport (UOT) and unbalanced entropic optimal transport (UEOT) solvers with the proposed U-LightOT solver. The comparison includes the principles behind each solver, the type of problem solved (UOT or UEOT), the solver’s output (what quantities are recovered), and the limitations of each approach. The table highlights that the proposed U-LightOT solver offers a theoretically justified, lightweight solution to the UEOT problem, in contrast to other methods that rely on heuristics or complex neural network architectures.

This table compares different existing unbalanced optimal transport solvers with the proposed U-LightOT solver. For each solver, it lists the type of problem solved (UOT or UEOT), the principles behind its design, the specific algorithm used, what aspect of the optimal transport plan the solver recovers (e.g., scaling factors, stochastic OT map), and any limitations of the approach. This allows for a clear comparison of the strengths and weaknesses of various methods in the field.

This table compares different UOT/UEOT solvers, including the proposed U-LightOT solver. It outlines the principles behind each solver’s approach to solving the problem (e.g., whether they use neural networks or regression), the type of problem they address (UOT or UEOT), what specific aspects of the optimal transport plan they recover, and the limitations of each approach. The table provides a concise overview of the state-of-the-art methods and highlights the advantages of the U-LightOT solver.

The table compares different existing unbalanced optimal transport (UOT) and unbalanced entropic optimal transport (UEOT) solvers with the proposed U-LightOT solver. For each solver, it lists the principle behind it (e.g., solving a max-min formulation using neural networks or using regression on discrete solutions), the problem it solves (UOT or UEOT), and what it recovers (e.g., scaling factors and OT maps). Finally, it mentions the limitations of each solver, such as using heuristic principles or requiring complex optimization procedures.

This table shows the test accuracy of keeping the class in the Adult → Young translation for different values of the unbalancedness parameter (τ) and entropy regularization parameter (ε). Higher accuracy indicates better preservation of the original class during the translation process. The results are presented as mean ± standard deviation.

This table compares different UOT/UEOT solvers, including their principles, the problem they solve, what they recover (e.g., scaling factors, OT maps), and their limitations. It highlights the differences in approaches and complexity of the existing methods before introducing the U-LightOT solver, which is the focus of this paper.

The table compares different existing unbalanced optimal transport (UOT) and unbalanced entropic optimal transport (UEOT) solvers with the proposed U-LightOT solver. For each solver, it lists the problem it solves, the principles used in its construction, what it recovers (e.g., scaling factors, optimal transport maps), and its limitations.

This table compares different UOT/UEOT solvers, including the proposed U-LightOT solver. It contrasts the principles behind each solver (e.g., whether it solves a max-min problem, uses neural networks, or relies on discrete OT approximations), the type of problem it solves (UOT or UEOT), and what it recovers (e.g., scaling factors, OT maps). Finally, it lists the limitations of each approach. This helps readers to understand the relative advantages and disadvantages of the proposed U-LightOT solver compared to other methods in the literature.

The table compares different existing unbalanced optimal transport solvers with the proposed U-LightOT solver in the paper. For each solver, it lists the principle, the problem it solves, the solver type, what it recovers (e.g., scaling factor, stochastic OT map), and limitations.

The table compares different existing unbalanced optimal transport (UOT) and unbalanced entropic optimal transport (UEOT) solvers with the proposed U-LightOT solver. For each solver, it lists the problem it solves, the principles used, what it recovers, and its limitations. The U-LightOT solver is highlighted as a novel, lightweight, and theoretically-justified approach.

This table compares the principles, solvers used, problems addressed, what is recovered by each approach, and the limitations of existing UOT/UEOT solvers with the proposed Light Unbalanced Optimal Transport (U-LightOT) solver. It highlights the differences in their approaches to solving unbalanced optimal transport problems, showing that U-LightOT offers a novel, theoretically justified, and lightweight solution compared to existing methods that often rely on heuristics or complex neural network architectures.

This table compares different existing unbalanced optimal transport (UOT) and unbalanced entropic optimal transport (UEOT) solvers with the proposed U-LightOT solver. For each solver, the table lists the problem it solves (UOT or UEOT), the principles it uses, the solver itself, what it recovers, and its limitations. The proposed solver (U-LightOT) is shown to be theoretically justified, lightweight and fast, in contrast to the others which use heuristic principles or heavy neural networks.

This table presents the Fréchet distance (FD) results for the Woman → Man image translation task using the U-LightOT solver. The FD metric measures the dissimilarity between the generated and target latent code distributions. Different values of the unbalancedness parameter (τ) and entropy regularization parameter (ε) are tested to observe their effect on the FD. Lower FD values indicate better similarity between the generated and target distributions.

The table compares different existing solvers for unbalanced optimal transport (UOT) and unbalanced entropic optimal transport (UEOT) problems. For each solver, it lists the problem it solves (UOT or UEOT), the principles it uses, the solver it employs, what it recovers (e.g., scaling factors, optimal transport maps), and its limitations. The table also includes information about the proposed U-LightOT solver, highlighting its advantages, such as its non-minimax optimization objective and lightweight nature.

The table compares different existing unbalanced optimal transport (UOT) and unbalanced entropic optimal transport (UEOT) solvers with the proposed U-LightOT solver in the paper. For each solver, it lists the problem it solves (UOT or UEOT), the principles behind its algorithm, what it recovers (e.g., scaling factors, optimal transport maps), and its limitations. The table highlights that existing solvers are often complex (using multiple neural networks) or heuristic, while the proposed U-LightOT solver is theoretically justified, lightweight, and efficient.

The table compares different existing unbalanced optimal transport (UOT) and unbalanced entropic optimal transport (UEOT) solvers with the proposed light solver (U-LightOT). For each solver, it presents the principles used, the problem it solves (UOT or UEOT), the type of solver, what the solver recovers (e.g., scaling factor, stochastic OT map), and the limitations of each solver. The comparison highlights that the proposed U-LightOT solver is lightweight, theoretically-justified and addresses the shortcomings of existing solvers.

The table compares different methods for solving the unbalanced optimal transport (UOT) problem, highlighting their principles, solvers, problems they solve, what they recover (e.g., scaling factors, OT maps), and their limitations. It shows that existing methods often rely on heuristics or complex neural networks, while the proposed U-LightOT method offers a theoretically justified, lightweight alternative.

This table compares different existing Unbalanced Optimal Transport (UOT) solvers with the proposed U-LightOT solver. It contrasts the principles behind each solver, the problem they solve (UOT or UEOT), the specific solver used, and what they recover (e.g., scaling factors, stochastic OT maps). Finally, it highlights limitations, such as complexity and reliance on heuristics.

This table compares different unbalanced optimal transport (UOT) and unbalanced entropic optimal transport (UEOT) solvers, including the novel U-LightOT solver proposed in the paper. The comparison covers the problem solved (UOT or UEOT), the principles behind each solver, the aspects of the optimal transport plan each solver recovers, and any limitations of the solvers. The table highlights that existing methods often rely on heuristics or complex neural network architectures, whereas U-LightOT offers a theoretically-justified, lightweight, and fast alternative.
Full paper#



















