↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Traditional nonparametric Bayesian methods for classification struggle with real-world data due to computational limitations and complex implementations. These models naturally handle open-ended classes and long-tailed distributions, but standard inference algorithms are computationally expensive and not designed for sequential inference, hindering their adoption in complex tasks. This paper addresses these challenges by using a recurrent neural network to learn the inductive bias inherent to the Bayesian model.
The proposed solution involves training a recurrent neural network (RNN) using data generated from a nonparametric Bayesian prior (Dirichlet Process Mixture Model). This “neural circuit” learns to perform Bayesian inference over an open set of classes. The method’s efficiency stems from the discriminative nature of RNNs, allowing it to make predictions in constant time for a sequence of observations. Experimental results demonstrate that the metalearned neural circuit achieves comparable or better performance than traditional approaches like particle filters, while requiring significantly less computation and being simpler to implement.
Key Takeaways#
Why does it matter?#
This paper is crucial because it presents a novel and efficient method for nonparametric Bayesian inference, a long-standing challenge in machine learning. Its approach of metalearning a neural circuit to emulate the inductive bias of Bayesian models offers significant improvements in speed and simplicity compared to traditional methods, opening up new possibilities for handling open-set classification problems in various domains. The work’s demonstrated success in complex image classification tasks and its potential applicability to other areas highlight its substantial impact on the field. It also bridges the gap between Bayesian models and deep learning, paving the way for more principled and efficient use of deep learning models for probabilistic tasks.
Visual Insights#

This figure illustrates the proposed method’s architecture. It involves two main stages: First, a recurrent neural network (RNN) is metalearned using data generated from a Dirichlet Process Mixture Model (DPMM). This metalearning process allows the RNN to learn the inductive bias of the DPMM. The second stage, ‘Attach,’ shows how this trained RNN is then used as a component in a larger nonparametric inference network. This network takes sequential inputs and uses the trained RNN to perform inference over a potentially unlimited number of classes, demonstrating the neural circuit’s capability for open-set classification.

This table presents a comparison of different methods for performing inference on two-dimensional data generated from a Dirichlet Process Mixture Model (DPMM). The methods compared are CRP, Softmax + Energy, Particle Filter, and the proposed Neural Circuit. The table shows the negative log-likelihood (NLL), perplexity, Adjusted Rand Index (ARI), Adjusted Mutual Information (AMI), and inference time for each method in both sequential observation and fully unobserved settings. Lower NLL and perplexity, and higher ARI and AMI indicate better performance. Lower inference time indicates higher efficiency.
In-depth insights#
Metalearned Inference#
The concept of “Metalearned Inference” presents a novel approach to Bayesian nonparametric inference by leveraging the power of meta-learning. Instead of directly implementing computationally expensive Bayesian methods, a recurrent neural network (RNN) is trained to mimic the behavior of a nonparametric Bayesian model like the Dirichlet Process Mixture Model (DPMM). This metalearning process involves training the RNN on numerous datasets sampled from the DPMM, enabling the network to internalize the model’s inductive bias. The resulting “neural circuit” then performs efficient inference, offering a significant speed-up compared to conventional methods. Crucially, this approach avoids the complexity and computational burden of explicit Bayesian calculations. This strategy provides a principled way to transfer the powerful inductive bias of Bayesian models to the realm of efficient, scalable neural networks, addressing a major limitation of nonparametric Bayesians in modern machine learning applications. However, careful consideration must be given to the choice of DPMM prior, and the generalization performance may vary depending on how closely the training and test data distributions match. Further investigation into these factors will be crucial in improving the reliability and expanding the applicability of this promising meta-learning based inference technique.
Neural Circuit Design#
Designing a neural circuit for nonparametric Bayesian inference presents a unique challenge, demanding a thoughtful blend of neural network architectures and Bayesian principles. The core idea involves metalearning, where a recurrent neural network (RNN) is trained on data generated from a Dirichlet Process Mixture Model (DPMM). This training process aims to instill the inductive biases inherent in the DPMM within the RNN, enabling the network to perform inference over an open-ended set of classes. The choice of an RNN is crucial, as its sequential nature elegantly handles the temporal aspect of sequential inference inherent in DPMM. The design must efficiently represent and update the posterior distribution over class assignments, avoiding the computational bottlenecks of traditional DPMM inference methods. Furthermore, the architecture must accommodate complex input data, such as images, requiring careful consideration of feature extraction and representation techniques. The success of this neural circuit hinges on the effectiveness of metalearning in transferring the desired inductive biases from the DPMM to the RNN. This requires rigorous testing and evaluation across a variety of datasets and scenarios, particularly those with open-ended class distributions. Ultimately, the design must strike a balance between computational efficiency and accuracy, leveraging the strengths of both neural networks and Bayesian methods for a robust and scalable inference system.
Open-Set ImageNet#
The concept of “Open-Set ImageNet” suggests an intriguing extension to the standard ImageNet challenge. It implies a shift from closed-set classification, where the model only encounters known classes during training and testing, to an open-set scenario. In this open-set setting, the model must not only correctly classify images belonging to known classes but also reliably identify images that represent previously unseen classes. This necessitates robust mechanisms for handling unknown data, going beyond simple rejection or assigning a default “unknown” label. Successful approaches might leverage techniques like anomaly detection, open-set recognition methods, or generative models to assess the novelty of input images. The difficulty arises in balancing accuracy on known classes with the ability to detect novel classes, often in a data-scarce setting. Such an open-set ImageNet would represent a significantly more realistic evaluation benchmark, pushing the boundaries of current computer vision techniques and prompting the development of more adaptable and robust models.
iNaturalist Robustness#
The evaluation of the model’s robustness on the iNaturalist dataset is a crucial aspect of the paper. It assesses the model’s ability to generalize beyond the data it was trained on (ImageNet), testing its resilience to distribution shifts. iNaturalist presents a more challenging scenario due to its long-tailed distribution and high inter-class similarity. The experiment’s design, using different taxonomic levels as class labels, systematically varies the complexity and class separation, allowing for a thorough assessment of generalization capabilities. The results demonstrate a degree of positive transfer, showing the model retains some predictive power on iNaturalist. However, the performance varies across taxonomic levels, highlighting the limitations in generalizing across drastically different data distributions. The analysis of the mismatched hyperparameter ‘alpha’ between ImageNet and iNaturalist training is a significant contribution, as it reveals how tuning this parameter impacts the performance on the target dataset. This nuanced analysis reveals limitations of direct transfer learning, and suggests areas for future improvement like more sophisticated domain adaptation techniques.
Future Extensions#
Future research directions stemming from this work could explore extending the metalearning framework to handle more complex nonparametric Bayesian models with richer latent variable structures. This might involve investigating different prior distributions or employing more sophisticated inference techniques within the RNN. Another promising area is developing methods to handle scenarios with substantial distribution shifts between meta-training and meta-testing data, enhancing the model’s robustness and generalization capabilities. This could involve incorporating techniques like domain adaptation or transfer learning. The efficiency of the training process is another crucial area; exploring more efficient optimization strategies or architectural innovations could lead to significant improvements. Finally, investigating the limits of scalability of the neural circuit for even larger datasets and more complex data modalities remains a vital consideration for future development, requiring careful consideration of computational resources and potential algorithmic bottlenecks. Addressing these extensions would broaden the applicability and impact of the proposed neural circuit for real-world applications.
More visual insights#
More on figures

This figure illustrates the architecture of the proposed nonparametric inference network. The network consists of three main components: a Dirichlet Process Mixture Model (DPMM) to generate data, a recurrent neural network (RNN) to learn the posterior distribution over class assignments via metalearning, and a nonparametric inference network that uses the learned RNN to perform sequential inference on unseen data. The RNN acts as a ’neural circuit,’ capturing the inductive bias from the DPMM and enabling efficient inference over an open-ended set of classes.
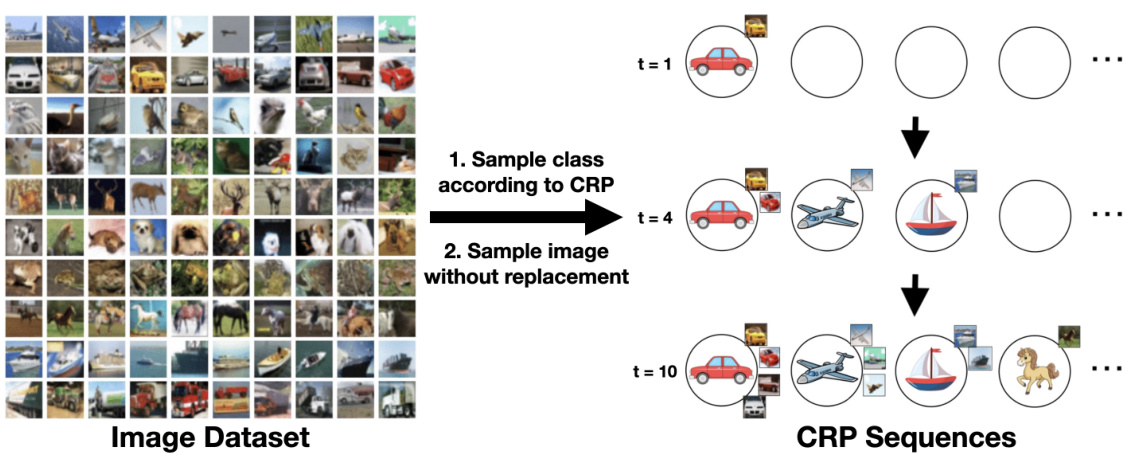
This figure illustrates the proposed metalearned neural circuit for nonparametric Bayesian inference. The process begins with data generated from a Dirichlet Process Mixture Model (DPMM), which represents a nonparametric Bayesian prior. This data is used to train a recurrent neural network (RNN). The trained RNN, referred to as a ’neural circuit,’ then captures the inductive bias from the DPMM. This allows the neural circuit to perform sequential inference over a potentially unlimited number of classes, effectively handling the open-set classification problem.

This figure illustrates the architecture of the proposed nonparametric inference network. The network consists of three main components: a Dirichlet Process Mixture Model (DPMM) to generate data, a Recurrent Neural Network (RNN) to model the posterior distribution over class assignments, and a nonparametric inference network that performs sequential inference. The RNN is metalearned by simulating data with the DPMM prior, allowing it to capture the inductive bias of the DPMM and perform inference over an unbounded number of classes. The figure showcases how the inductive bias from a nonparametric Bayesian model is transferred to a neural network to facilitate efficient and scalable inference.
More on tables
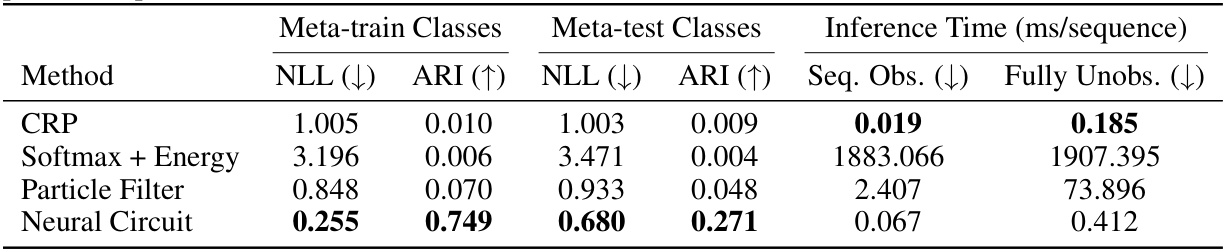
This table presents the results of the open-set classification experiments on ImageNet-CRP using ResNet-18 features. It compares the performance of four methods: CRP (Chinese Restaurant Process), Softmax + Energy (a non-Bayesian baseline), Particle Filter, and the proposed Neural Circuit. The metrics include negative log-likelihood (NLL), adjusted Rand index (ARI) for both meta-train and meta-test classes, and inference time per sequence for both sequential observation and fully unobserved settings. The Neural Circuit significantly outperforms other methods in terms of both accuracy and speed.
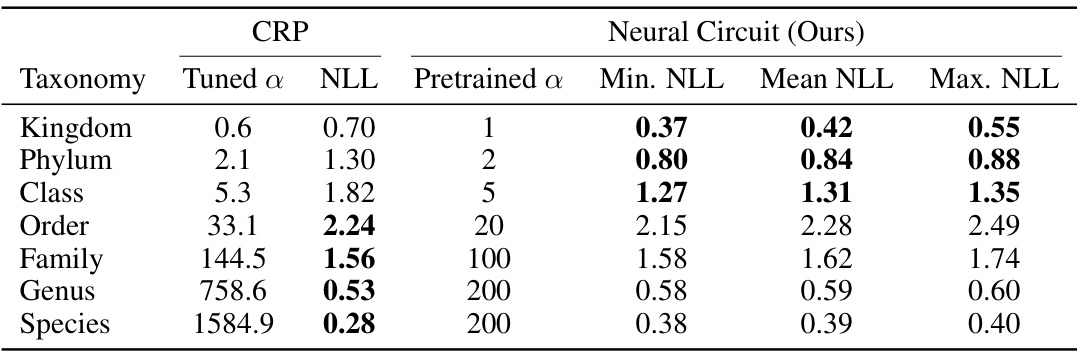
This table presents the results of transferring a model trained on ImageNet-CRP data to the iNaturalist 2018 dataset. It compares the performance of the CRP baseline (with a tuned hyperparameter α) against the neural circuit model (with a hyperparameter α chosen to match the CRP’s as closely as possible). The comparison is performed across seven taxonomic levels of the iNaturalist data, evaluating the average negative log-likelihood (NLL) per timestep. Minimum, mean, and maximum NLL values across five runs with different random seeds are shown to illustrate variability.
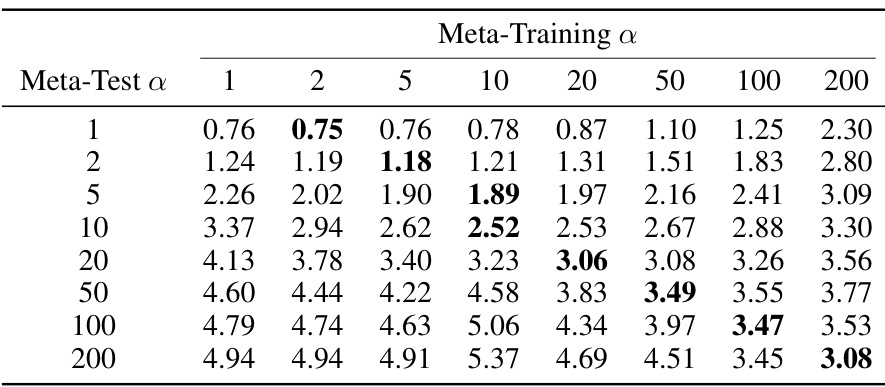
This table presents the negative log-likelihood (NLL) results for the ImageNet-CRP meta-test classes under various meta-training conditions. The evaluation was done on 1000 sequences of length 500, and the table shows how the NLL changes with different combinations of meta-training and meta-test hyperparameter ‘a’. Each cell represents the average NLL for a specific combination of meta-training and meta-test ‘a’ values.

This table presents the results of experiments comparing different methods for performing inference in a Dirichlet Process Mixture Model (DPMM) on a synthetic dataset with two-dimensional data. The methods compared are a Chinese Restaurant Process (CRP) baseline, a Softmax + Energy baseline, a Particle Filter method, and the proposed Neural Circuit method. The table shows the negative log-likelihood (NLL), perplexity, Adjusted Rand Index (ARI), Adjusted Mutual Information (AMI), and inference time for both sequential observation and fully unobserved settings. The results demonstrate the superior performance of the Neural Circuit in terms of both accuracy and speed.
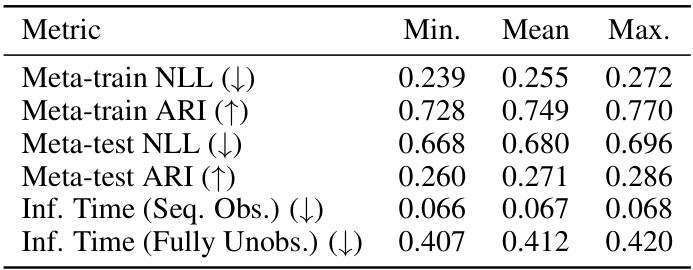
This table presents the results of open-set classification experiments on ImageNet-CRP dataset using ResNet-18 activations. It compares the performance of the proposed neural circuit against baselines (CRP, Softmax + Energy, and Particle Filter) across multiple metrics. The metrics include negative log-likelihood (NLL), adjusted Rand index (ARI) for meta-train and meta-test sets, and inference time for sequential observation and fully unobserved settings.
Full paper#