↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
The core problem is computing the geometric median of a dataset while preserving differential privacy. Existing methods, like DP-SGD, have accuracy guarantees that depend linearly on the a priori bound of the data, which can be problematic because it does not reflect the actual scale of the majority of the data. This paper introduces two polynomial-time algorithms, LocDPSGD and LocDPCuttingPlane, which improve upon this limitation and offer multiplicative instead of additive excess error guarantees that scale with the effective diameter of the data, thus exhibiting robustness against outliers. Additionally, an inefficient pure DP algorithm, SInvS, is also presented.
The algorithms work in two phases: a warm-up phase that privately estimates the effective data diameter and finds a good initialization point, followed by a fine-tuning phase that refines the approximation. The authors complement their work with a lower bound on the sample complexity and demonstrate the optimality of their polynomial-time algorithms. The results are theoretically supported by rigorous proofs and demonstrated via numerical experiments showing improvement over DP-SGD.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in differential privacy and machine learning because it presents novel algorithms for computing the geometric median with improved accuracy guarantees. It directly addresses the limitations of existing methods by providing algorithms whose accuracy scales with the effective diameter of the data, rather than the worst-case bound. This advancement significantly enhances the practicality and robustness of differentially private data analysis, opening new avenues for research and applications in various sensitive data domains.
Visual Insights#
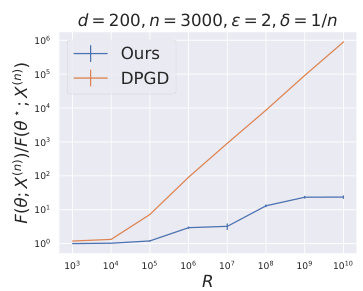
The figure shows the performance comparison between the proposed algorithm (Ours) and DP-GD for different privacy budgets. The x-axis represents the radius R of the data, and the y-axis represents the ratio of the loss function value obtained by each algorithm to the optimal loss function value. The figure demonstrates that the proposed algorithm is more robust to changes in the radius R compared to DP-GD, especially for larger values of R.

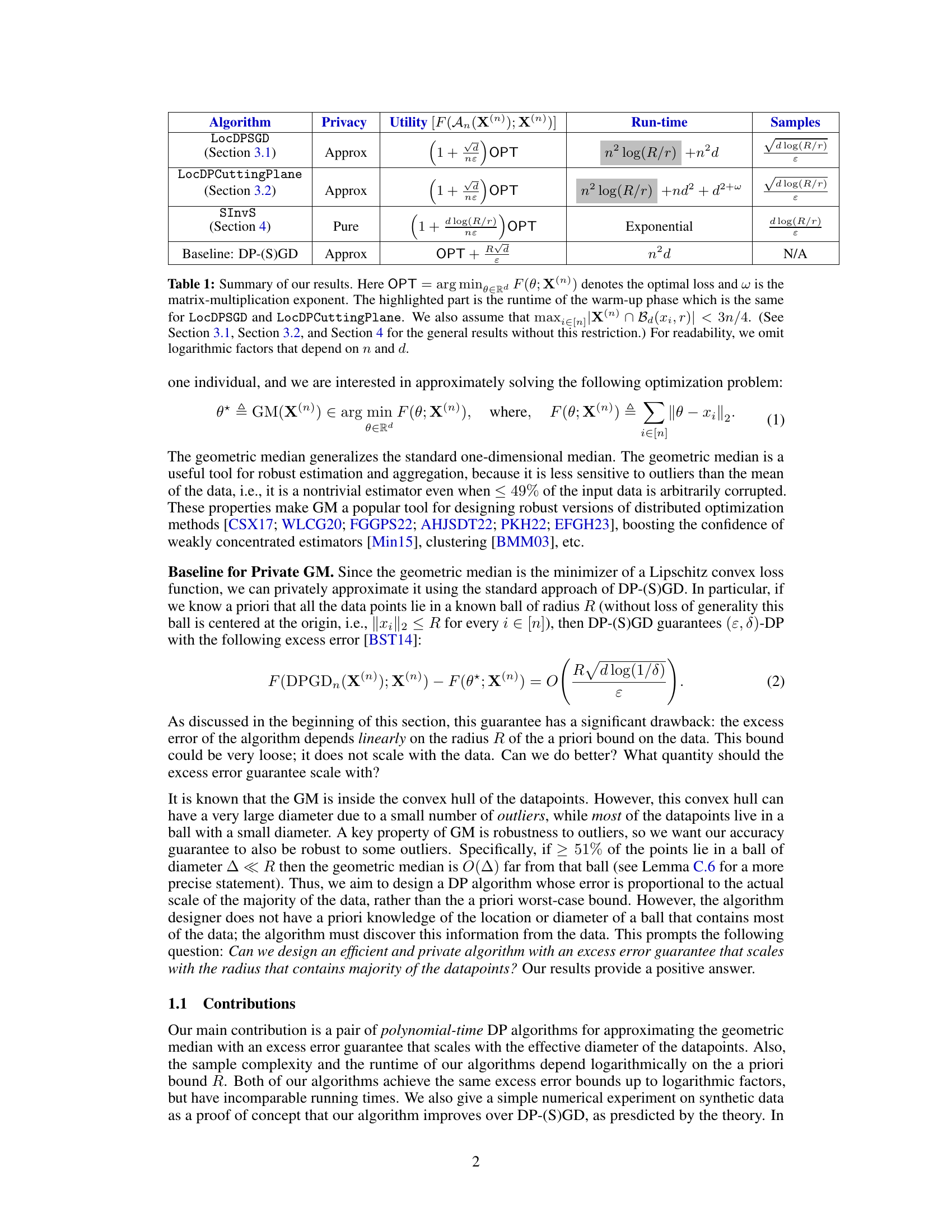
This table summarizes the performance of different algorithms for approximating the geometric median under differential privacy. It compares algorithms in terms of their approximation quality (utility), privacy guarantees, runtime, and sample complexity requirements. The algorithms include our proposed LocDPSGD and LocDPCuttingPlane methods, as well as an inefficient algorithm based on inverse sensitivity and the baseline DP-SGD approach. The table highlights the efficiency improvements of the proposed algorithms.
In-depth insights#
Private GM Algo#
The heading ‘Private GM Algo’ likely refers to a section detailing algorithms for computing the geometric median (GM) under differential privacy constraints. This is a significant problem because directly applying standard GM algorithms leaks sensitive information. The paper likely explores novel approaches that add carefully calibrated noise to the data or the algorithm’s computations, balancing privacy guarantees with accuracy. Several algorithmic strategies might be compared, possibly including those that adapt to the data’s characteristics, such as using a quantile radius to bound the effect of outliers. The in-depth analysis may involve examining privacy parameters (ε, δ), establishing bounds on the error introduced by the privacy mechanisms, and potentially providing runtime and sample complexity analysis for each algorithm. Crucially, the discussion would need to demonstrate the algorithms’ efficiency and theoretical guarantees while maintaining a strong privacy level.
Quantile Radius#
The concept of “Quantile Radius” offers a robust and adaptive approach to handling data uncertainty in private geometric median computations. Unlike traditional methods relying on a priori bounds, Quantile Radius dynamically estimates the scale of the data, focusing on the radius encompassing a specified quantile (e.g., 51%) of the points. This is crucial because it mitigates the impact of outliers and focuses on the data’s inherent structure rather than arbitrary worst-case scenarios. The effectiveness of this approach is underscored by the algorithm’s improved excess error guarantees, scaling with the quantile radius rather than the overall dataset’s maximum extent. This scale-free property enhances the algorithm’s adaptability to varied data distributions, yielding accurate results even under high uncertainty.
DP Cutting Plane#
Differentially Private (DP) Cutting Plane methods offer a promising approach to private optimization problems, particularly when dealing with high-dimensional data. The core idea involves iteratively refining a feasible region by incorporating noisy cuts, obtained via a differentially private mechanism. This approach leverages the power of cutting plane techniques, known for their efficiency in solving convex optimization problems, while maintaining privacy guarantees. A crucial challenge is managing the noise inherent in the private cuts, which can significantly affect the accuracy and convergence of the algorithm. Careful selection of noise levels and potentially incorporating adaptive noise mechanisms are vital. The trade-off between privacy and utility is central to algorithm design, requiring a balance between strong privacy guarantees and reasonable accuracy. Analyzing the convergence rates and sample complexity under various privacy settings is crucial to understanding the effectiveness of DP Cutting Plane algorithms. Furthermore, comparison to other DP optimization methods, such as DP-SGD, allows for evaluating its strengths and weaknesses under different data characteristics and problem complexities.
Pure DP GM#
The heading ‘Pure DP GM’ suggests a research direction focused on achieving pure differential privacy (DP) guarantees for the geometric median (GM) problem. This is a significant advancement because pure DP offers stronger privacy protection compared to approximate DP, which allows for a small probability of privacy violation. The geometric median is a robust estimator, making it attractive for applications with potentially noisy or outlier-prone data. However, developing a pure DP mechanism for GM is inherently challenging, as it requires careful consideration of the sensitivity of the GM calculation. The research likely explores techniques like the smooth sensitivity mechanism or advanced composition methods to achieve pure DP while maintaining reasonable utility. Success would demonstrate a powerful technique applicable to robust estimation in privacy-sensitive contexts and offers significant contributions to the field of privacy-preserving data analysis. However, it’s anticipated that pure DP might come at the cost of increased computational complexity compared to approximate DP solutions, which is another crucial aspect the research probably addresses.
Future Work#
A promising area for future work is exploring the applicability of the proposed algorithms to more complex datasets and real-world problems. This includes investigating the algorithm’s performance in high-dimensional settings, with non-convex loss functions, or in the presence of significant outliers or noise. Another crucial aspect is developing faster algorithms for large-scale datasets, perhaps by leveraging techniques like distributed optimization or approximation algorithms, while still maintaining strong privacy guarantees. Furthermore, it is important to conduct extensive empirical evaluation on real-world datasets across multiple domains to solidify the algorithm’s practical utility and robustness. Finally, theoretical analysis could be extended to provide tighter bounds on the excess error and a deeper understanding of the sample complexity, potentially by incorporating advanced techniques from statistical learning theory.
More visual insights#
More on figures

This figure provides a geometrical intuition behind Equation (57) in Section 4. It illustrates how the distance between the geometric median (GM(X)) and the true geometric median (θ*) is related to the quantile radius (Δγn(θ*)). Specifically, it demonstrates that if ||θ − θ*|| > Δγn(θ*), then ||∇F(θ; X)|| is lower bounded by a function of m and ||θ − θ*||, where m is the number of data points within a ball of radius Δγn(θ*) centered at θ*. This bound helps to establish a relationship between the excess error and the quantile radius.

The figure shows the performance comparison between the proposed algorithm (Ours) and DP-GD for different privacy budgets (ε=2 and ε=3). The x-axis represents the radius (R) of the data distribution, and the y-axis represents the ratio of the loss function value for the chosen algorithm to the optimal loss function value. The plots illustrate how the algorithms’ performance changes as the dataset’s scale increases, particularly highlighting how the proposed algorithm degrades more gracefully than DP-GD when R increases.
Full paper#