↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Deep reinforcement learning (DRL) uses powerful neural networks, but their output predictions can unexpectedly change after each training update, leading to instability. This phenomenon, known as “churn,” is particularly problematic in RL because of its non-stationary nature, potentially causing suboptimal performance and even learning collapse. Existing methods often focus on addressing individual aspects of the problem, such as value function approximation error or policy updates, but they often neglect the interconnected nature of the learning process.
This paper introduces a new method called CHAIN (Churn Approximated Reduction) to directly mitigate churn by reducing changes to policy and value network outputs for states outside of the current training batch. CHAIN can be easily integrated into many existing DRL algorithms with minimal code changes. Experiments across various environments and algorithms consistently demonstrate CHAIN’s efficacy in reducing churn and improving learning performance, especially regarding sample efficiency and scalability of DRL agents.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles the instability and inefficiency in deep reinforcement learning (DRL), a major obstacle to its broader application. By identifying and mitigating the “chain effect” of value and policy churn, the research opens up new avenues for improving the stability, sample efficiency, and scalability of DRL agents. It directly addresses current challenges in the field and provides practical solutions, making it highly relevant for researchers and practitioners alike.
Visual Insights#
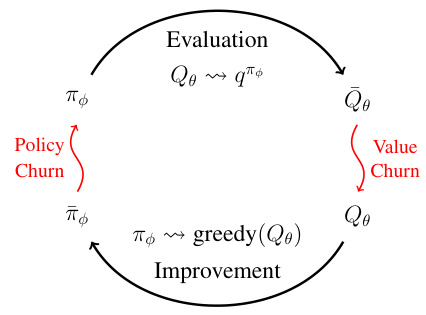
This figure illustrates the Generalized Policy Iteration (GPI) process with the inclusion of value and policy churn. The standard GPI cycle of evaluation and improvement is shown, but with the addition of red curly arrows representing the churn phenomena. The evaluation phase involves approximating the value function Q using the current policy πφ, but this approximation is not perfect due to value churn (Qo → Qe). The improvement phase involves updating the policy based on the approximated value function Qe, which leads to a new policy πφ. However, this new policy is not precisely the expected greedy policy due to policy churn (πφ → πφ). The loop continues iteratively, but the churns introduce imprecision and bias in the process.
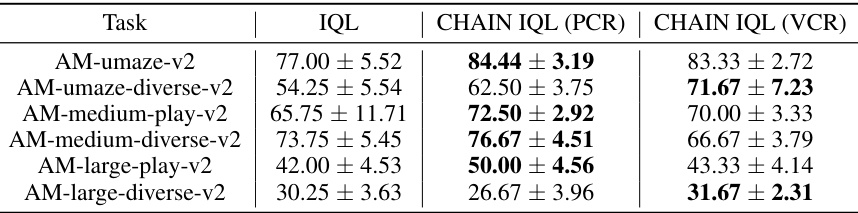
This table presents the results of the IQL algorithm and its variations with CHAIN in Antmaze environment. Three variations of the IQL algorithm are compared: the original IQL, IQL with policy churn reduction (CHAIN IQL (PCR)), and IQL with value churn reduction (CHAIN IQL (VCR)). The table shows the mean and standard error of the performance (presumably an average reward or score) across twelve different random seeds for each algorithm and across six different Antmaze tasks (AM-umaze-v2, AM-umaze-diverse-v2, AM-medium-play-v2, AM-medium-diverse-v2, AM-large-play-v2, and AM-large-diverse-v2). This allows for a comparison of the performance improvement resulting from the application of the CHAIN method to reduce churn.
In-depth insights#
Chain Effect of Churn#
The concept of “Chain Effect of Churn” in reinforcement learning (RL) describes a cyclical feedback loop where initial prediction errors or instability (churn) in either value or policy estimations amplify subsequent updates. Value churn, caused by imprecise value function approximation, leads to greedy action deviations in value-based methods. This, in turn, influences the policy leading to policy churn. Policy churn, in turn, further impacts value estimation in the next iteration, creating a compounding effect. This feedback loop can manifest as trust region violations in policy-based methods and dual bias in actor-critic methods. The chain effect highlights the interconnectedness and potential instability introduced by using neural networks as function approximators in RL. Effectively managing churn is crucial to improving learning stability and overall performance, underscoring the need for algorithms and techniques to mitigate the chain reaction.
DRL Churn Analysis#
Analyzing Deep Reinforcement Learning (DRL) churn involves investigating the phenomenon where network predictions fluctuate unpredictably between training updates. A key aspect is understanding the causes of this instability, which could stem from the non-stationary nature of DRL and the inherent limitations of function approximators. By characterizing churn within the Generalized Policy Iteration framework, the paper likely reveals a ‘chain effect’ where value and policy estimations interact and compound errors. This chain effect might manifest in various ways, such as greedy action deviations in value-based methods, trust region violations in policy optimization algorithms, or dual biases in actor-critic models. Effective mitigation strategies are crucial for improving learning stability and performance, possibly involving regularization methods to control the undesirable changes in network outputs. Empirical validation across different DRL algorithms and environments is vital for demonstrating the impact of churn and the efficacy of proposed solutions. Ultimately, a thorough DRL churn analysis should illuminate the fundamental limitations of DRL and guide the development of more robust and efficient algorithms.
CHAIN Method#
The CHAIN (Churn Approximated ReductIoN) method is a novel technique designed to mitigate the detrimental effects of value and policy churn in deep reinforcement learning (DRL). Churn, characterized by unpredictable changes in network outputs after each training batch update, is addressed by CHAIN through a regularization approach. Instead of directly controlling the network’s dynamics, CHAIN minimizes unintended changes to the outputs of the policy and value networks for states outside the current training batch. This is achieved by introducing a secondary loss function that penalizes large discrepancies between target values across consecutive iterations. The main idea is to maintain stability and improve generalization, preventing the compounding effect of churn that can hinder learning. CHAIN’s effectiveness is demonstrated across diverse DRL settings and environments, including value-based and policy-based methods, showcasing its versatility and practicality. Its simplicity and ease of implementation allow for easy integration into existing algorithms, highlighting its potential as a valuable tool for enhancing the robustness and efficiency of DRL.
DRL Scaling#
The research paper explores the challenges of scaling Deep Reinforcement Learning (DRL) agents. Simply increasing network size often leads to performance degradation or even collapse. The authors hypothesize that uncontrolled value and policy churn, a phenomenon where network outputs unexpectedly change during training, is a significant contributing factor. Their proposed method, CHAIN, aims to mitigate this churn by introducing regularization techniques, thus improving learning stability and allowing for successful scaling. Experimental results show CHAIN enables better scaling of DRL agents across different algorithms and environments, suggesting that controlling churn is crucial for effective scaling. This work makes a novel contribution by directly addressing the link between churn and the difficulty of scaling DRL, offering a practical solution for improving learning performance and generalization in larger models. The authors’ findings highlight the importance of considering internal learning dynamics when designing and training deep RL agents.
Future of CHAIN#
The “Future of CHAIN” holds exciting possibilities. Extending CHAIN’s applicability beyond the current RL algorithms and environments is crucial. This involves thorough testing on a wider range of tasks, including those with complex state spaces or continuous actions. Further investigation into the theoretical underpinnings of CHAIN is needed to better understand its effectiveness and limitations. This requires more rigorous mathematical analysis and exploration of the interplay between churn and other aspects of RL. Adaptive mechanisms for automatically tuning CHAIN’s hyperparameters would improve usability. Current methods require manual adjustment, limiting broad applicability. Research into robust, data-driven tuning strategies is a high priority. Finally, investigating CHAIN’s interaction with other techniques for improving RL stability and scalability is vital. This could include integrating CHAIN with novel architectures, representation learning methods, or improved experience replay methods. The long-term success of CHAIN depends on addressing these key areas.
More visual insights#
More on figures

This figure illustrates the Generalized Policy Iteration (GPI) process in reinforcement learning, highlighting the impact of value and policy churn. The standard GPI process involves alternating between policy evaluation and policy improvement steps. This figure extends this model to incorporate the concept of ‘churn’, which refers to the unexpected changes in the network outputs on states not directly updated in a mini-batch. The figure shows that both value churn (changes in the value function) and policy churn (changes in the policy) occur and influence each other throughout the iterations. It emphasizes the intertwined nature of these churns and how they affect each step of the GPI process.

This figure shows the impact of CHAIN on reducing value churn and greedy action deviation in the Breakout game. The left panel shows the value churn, which measures the change in Q-values for states not directly updated by mini-batch training. The right panel shows the percentage of greedy actions that changed after each update. The results indicate that CHAIN effectively reduces both value churn and greedy action deviation.

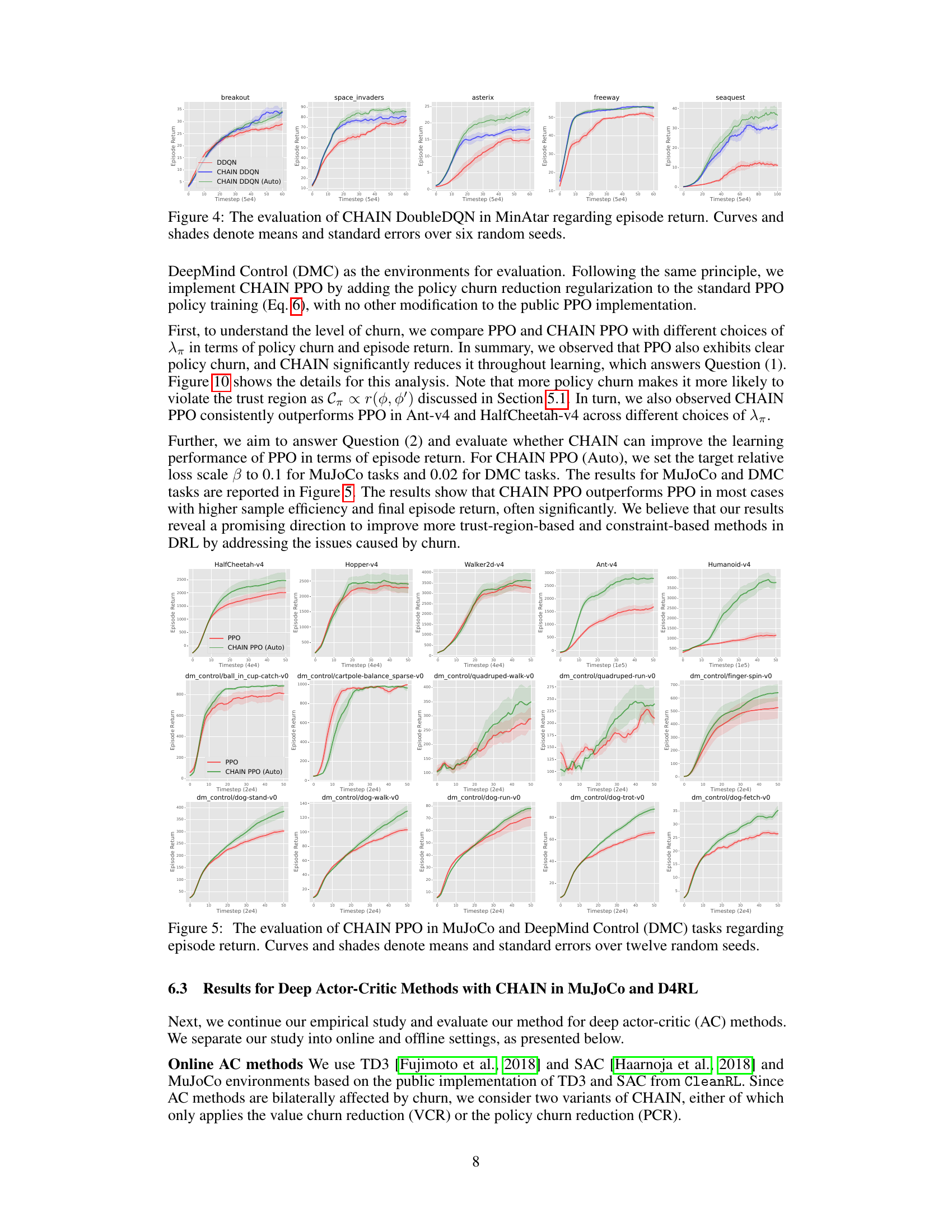
This figure shows the learning curves for the CHAIN DoubleDQN algorithm and the standard DoubleDQN algorithm across five different MinAtar environments. The x-axis represents training timesteps, and the y-axis represents the average episode return. Each line represents the average performance across six different random seeds, with shaded regions indicating the standard error. The figure demonstrates that CHAIN DoubleDQN consistently outperforms the standard DoubleDQN algorithm in terms of both sample efficiency and final performance across all environments.
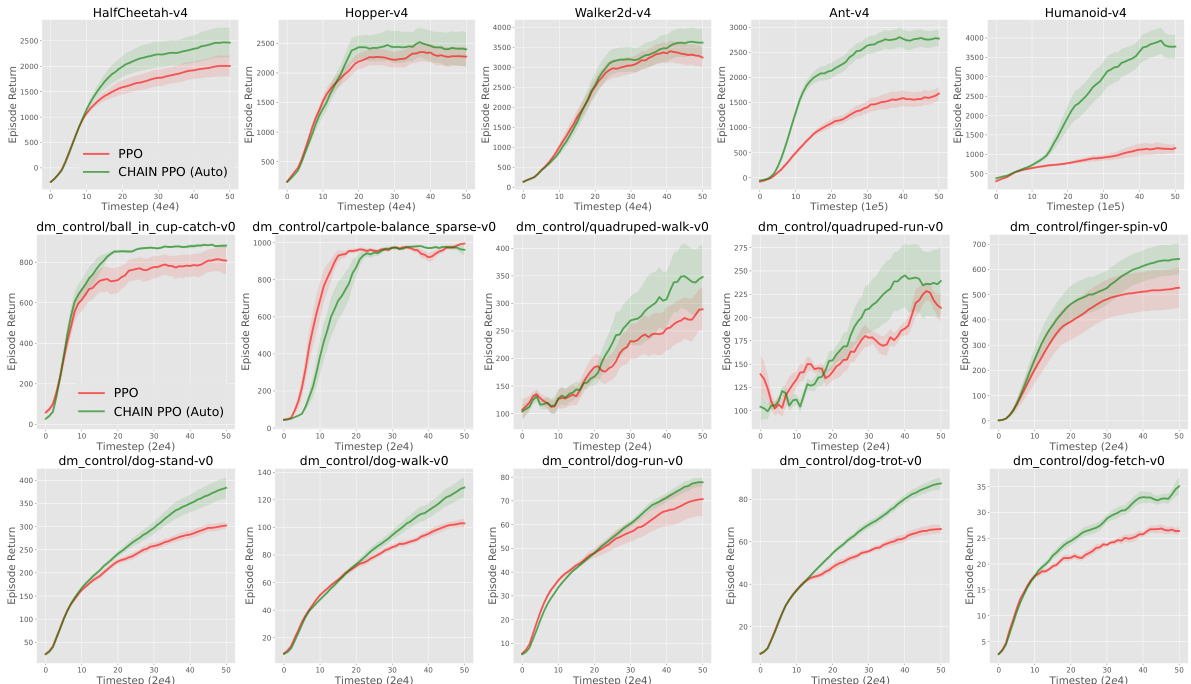
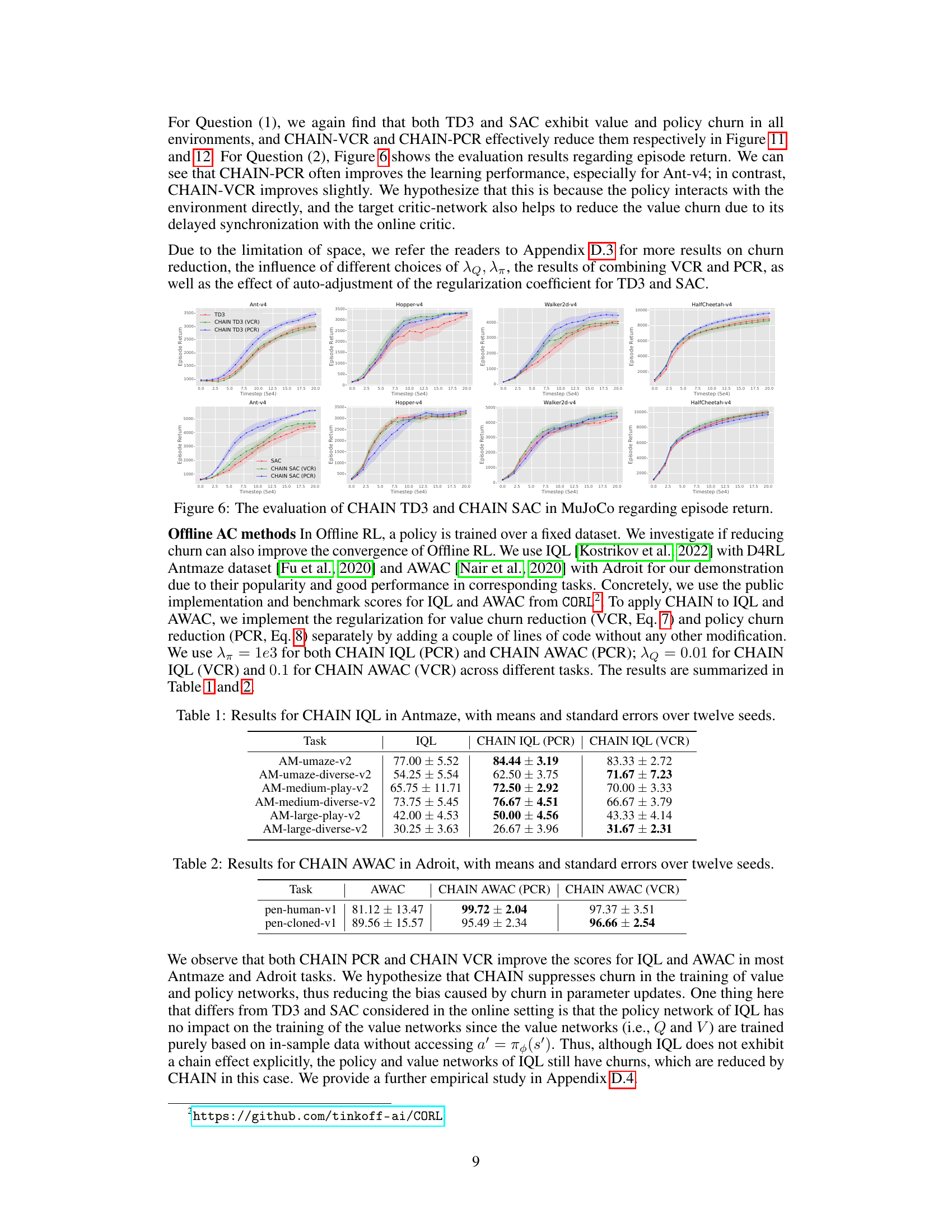
This figure presents the results of applying the CHAIN method to Proximal Policy Optimization (PPO) on various continuous control tasks from MuJoCo and DeepMind Control Suite (DMC). It shows the learning curves (episode return) for both standard PPO and CHAIN PPO, with error bars indicating standard errors across multiple random seeds. The results demonstrate that CHAIN PPO generally outperforms standard PPO, highlighting the effectiveness of CHAIN in improving learning performance across these environments.
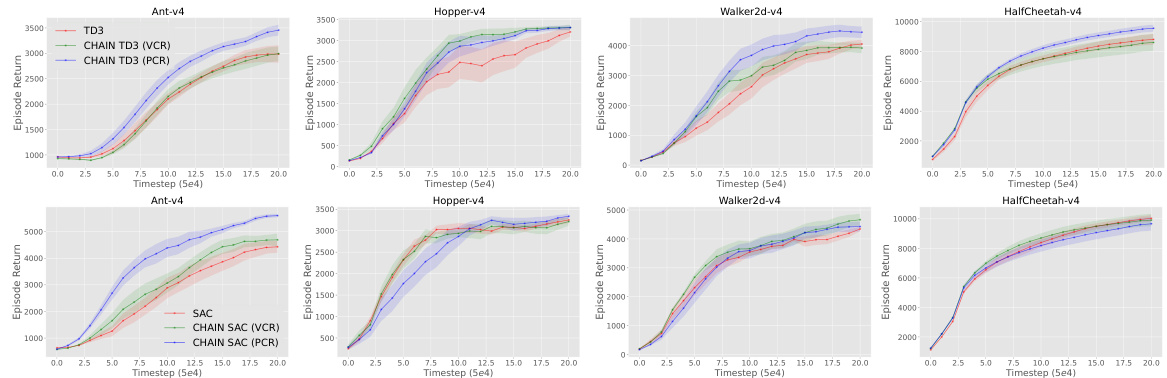
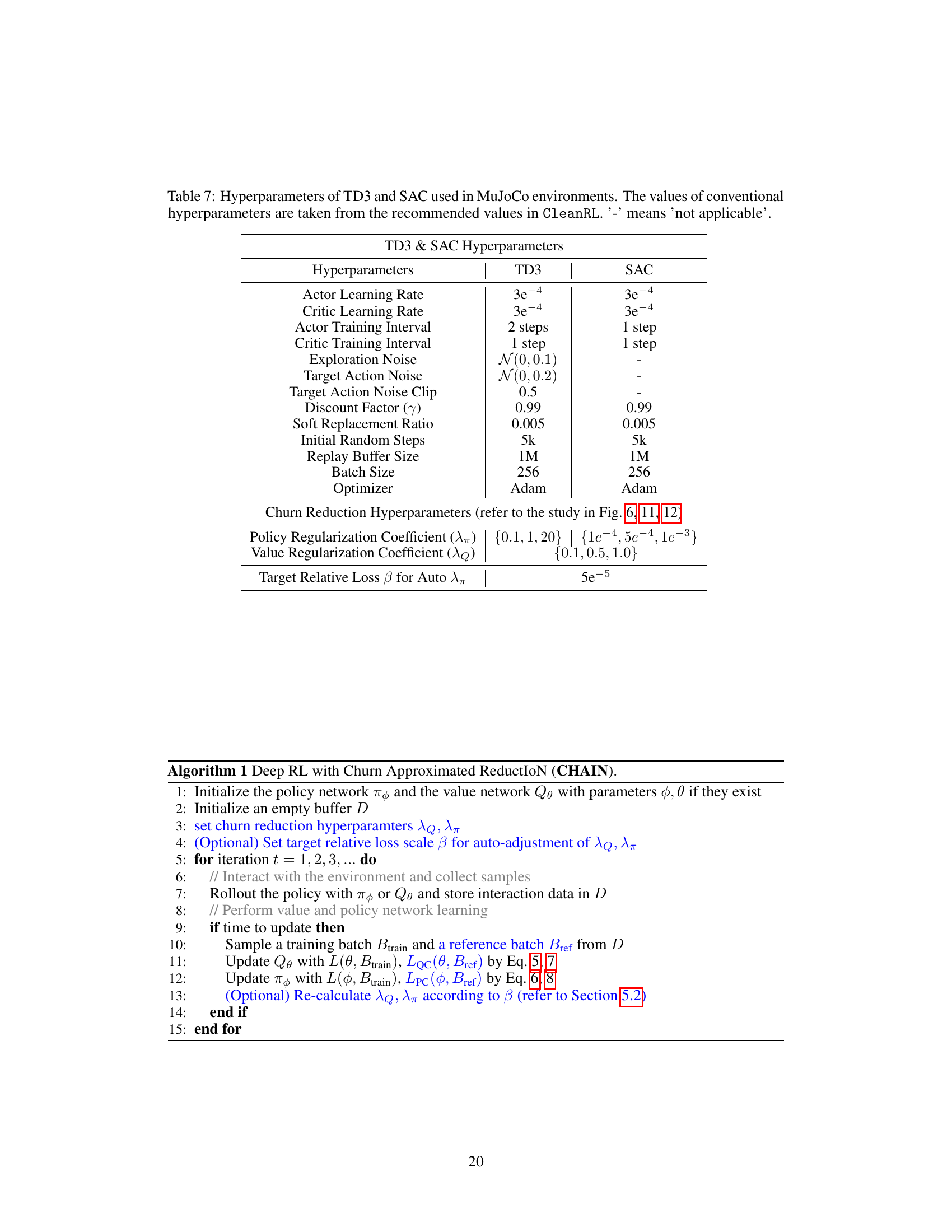
This figure shows the results of applying CHAIN (VCR and PCR) to TD3 on four MuJoCo tasks. The plots show the episode return over time, along with the value churn, policy churn, and policy value deviation. The results demonstrate that CHAIN effectively reduces the value and policy churn in all four tasks, leading to improved learning performance. The figure also includes error bars to show statistical significance.

This figure shows the results of scaling PPO by widening the network. The x-axis represents the scale-up ratio, and the y-axis represents the episode return. Four different scenarios are plotted: standard PPO, PPO with a reduced learning rate (sqrt_lr), CHAIN PPO, and CHAIN PPO with a reduced learning rate (sqrt_lr). The results demonstrate that CHAIN improves the scaling performance of PPO across different scale-up ratios and learning rates, mitigating the performance degradation typically observed when scaling up DRL agents.
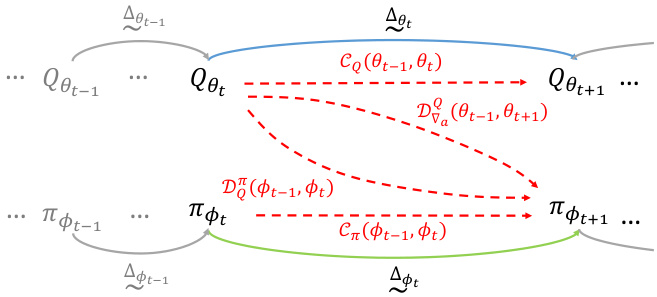
This figure illustrates the Generalized Policy Iteration (GPI) process, a common framework in reinforcement learning, but with the added consideration of value and policy churn. The standard GPI alternates between policy evaluation (estimating the value function) and policy improvement (updating the policy based on the estimated value). This figure highlights that churn in both the policy evaluation and improvement steps creates a feedback loop where changes in one step influence the next. The value churn (Qo → Qe) alters the value function, impacting the policy improvement. The policy churn (πφ ↔ πφ) changes the policy, leading to a new value function estimation. This interplay of value and policy churn creates a chain reaction that biases the learning process.
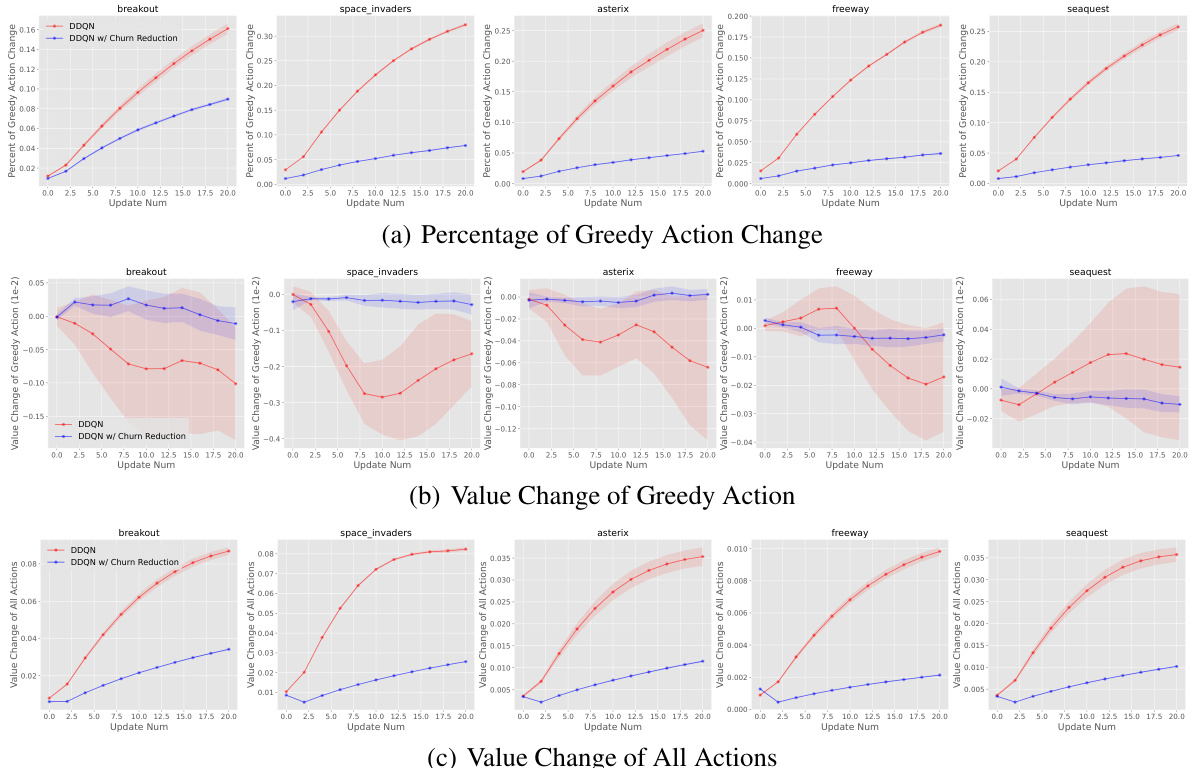
This figure presents an empirical analysis of the value churn in the DoubleDQN algorithm applied to the MinAtar environment. It displays three key metrics over the course of training: the percentage of greedy actions that change after each update, the value change of the greedy action, and the overall value change of all actions. The shaded areas represent standard error across six different training runs. The figure helps to visualize how the value churn accumulates during training and how it is affected by the proposed Churn Approximated Reduction (CHAIN) method.
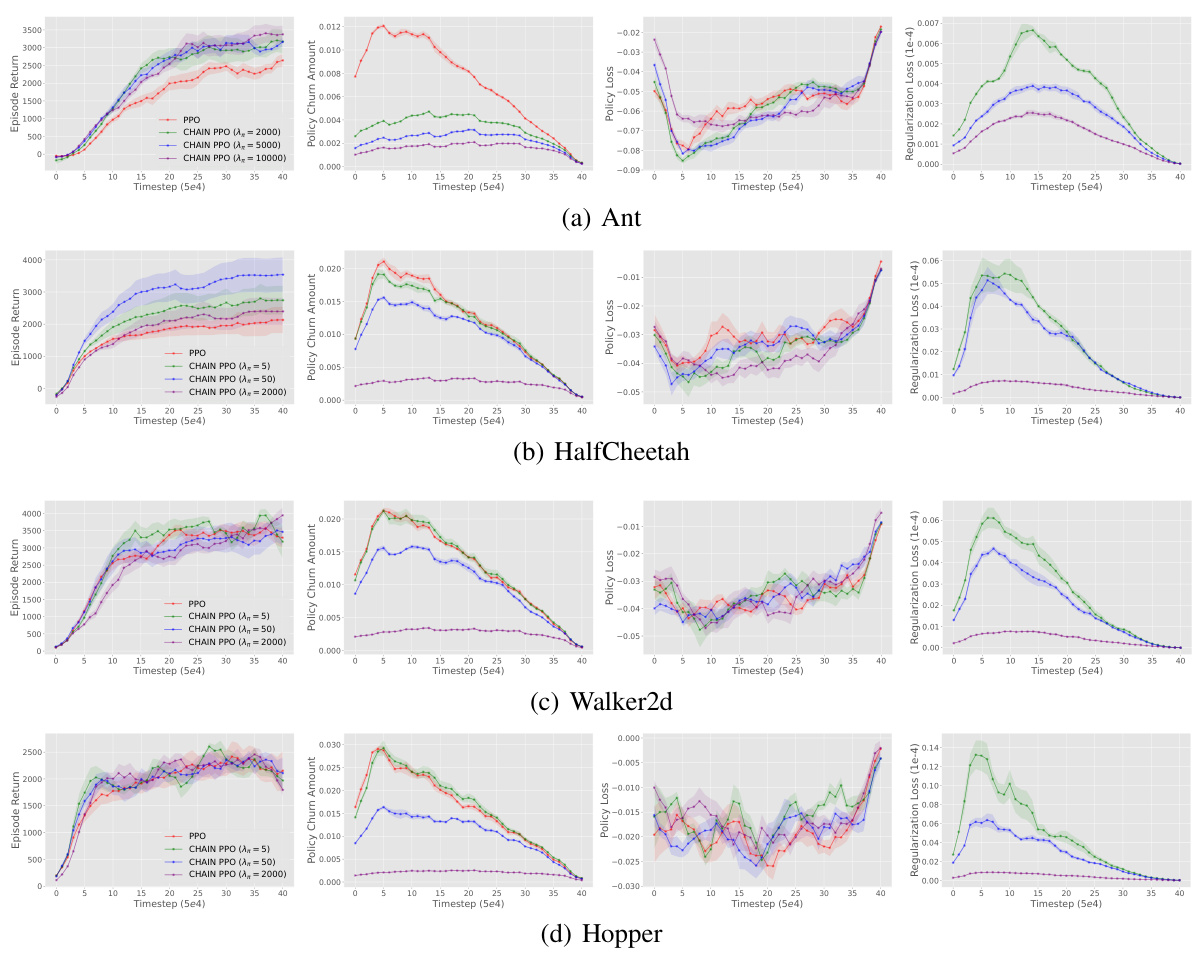
This figure presents the results of CHAIN PPO applied to four MuJoCo tasks. For each task, four sub-figures are shown: episode return, policy churn amount, policy loss, and regularization loss. Each sub-figure displays the performance of standard PPO and CHAIN PPO using different hyperparameters (λπ = 5, 50, 2000). The results show that CHAIN PPO generally reduces policy churn and improves learning performance compared to standard PPO, demonstrating the effectiveness of the CHAIN method in controlling policy churn and improving learning outcomes.

This figure shows the results of applying the CHAIN method to TD3 on four MuJoCo locomotion tasks. It presents four plots for each task, visualizing the episode return, absolute value churn, value churn of greedy action, policy churn and policy value deviation over training iterations. The plots illustrate how CHAIN reduces the various types of churn and improves the learning performance.
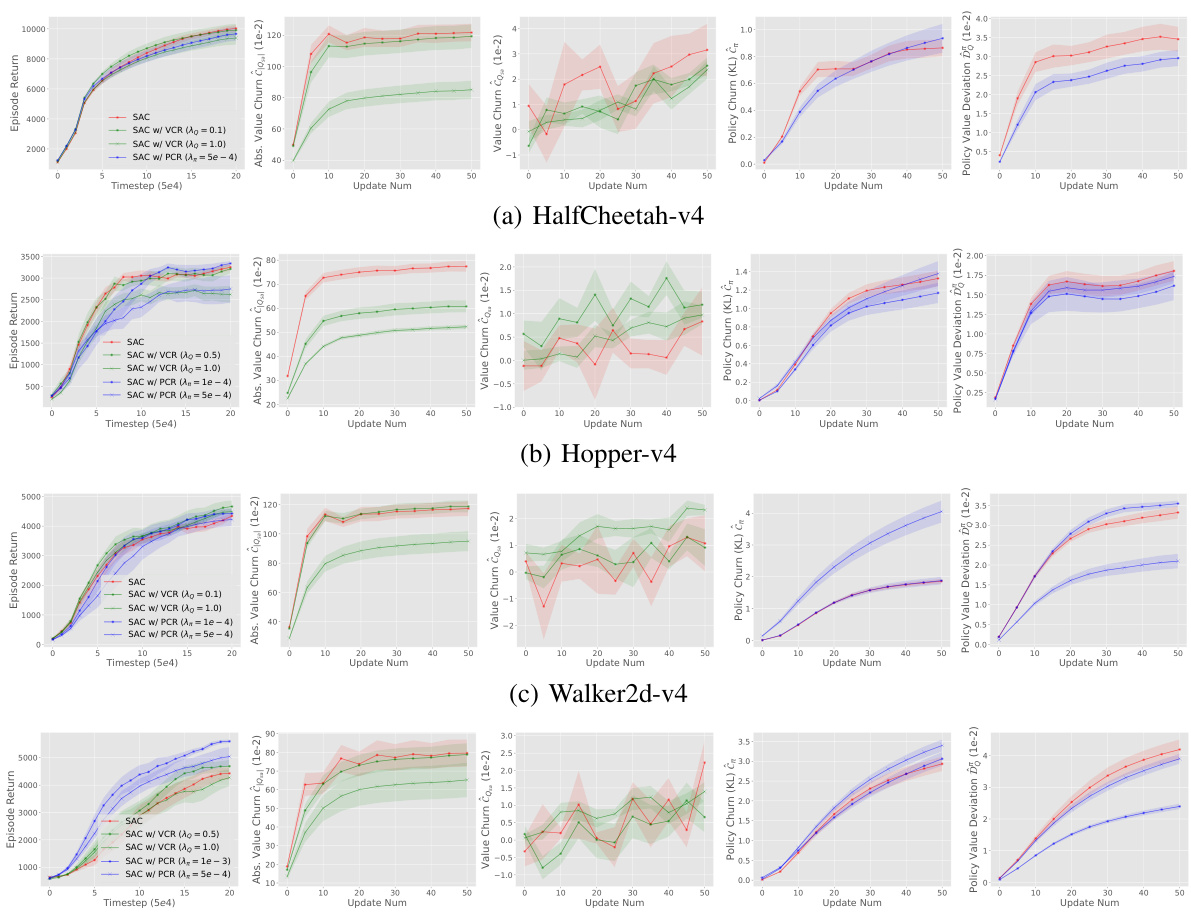
This figure shows the results of applying the CHAIN method to TD3 in four MuJoCo environments: HalfCheetah-v4, Hopper-v4, Walker2d-v4, and Ant-v4. For each environment, the figure displays the episode return, absolute value churn, policy churn (measured using KL divergence), and policy value deviation over the course of training. Different lines represent different variations of the CHAIN method (VCR, PCR, or both) with differing hyperparameters. The results illustrate the effectiveness of CHAIN in reducing churn and improving performance in these tasks.

This figure shows the effects of applying different churn reduction methods (VCR, PCR, and DCR) on TD3 in MuJoCo environments. It displays the changes in various metrics related to value and policy churn, including the value churn, policy churn, and value deviation of policy churn, across multiple time steps. The results illustrate how the proposed methods reduce the level of churn, supporting the paper’s claim.

This figure displays the learning curves of PPO and CHAIN PPO on four MuJoCo tasks, along with the policy churn, policy loss, and regularization loss. It demonstrates CHAIN PPO’s ability to reduce policy churn and improve learning performance in Ant-v4 and HalfCheetah-v4, while maintaining comparable performance in Hopper-v4 and Walker2d-v4. The results are shown for different choices of the hyperparameter λπ (lambda-pi), which controls the strength of the policy churn regularization.

This figure shows the effect of different hyperparameter choices for value and policy churn reduction regularization on TD3’s performance across four MuJoCo locomotion tasks. The hyperparameters λθ and λπ control the strength of the value and policy churn reduction terms, respectively. The figure visualizes the learning curves (episode return) for various combinations of these hyperparameters, showcasing how different settings impact the learning process. Error bars indicate the standard deviation across multiple runs for each setting, offering insight into the robustness and stability of different parameter choices.

This figure shows the learning curves for CHAIN DoubleDQN and the standard DoubleDQN on six different MinAtar games. The x-axis represents training timesteps, and the y-axis represents the average episode return. Each line represents the average performance across six different random seeds, with shaded regions indicating the standard error. The results show that CHAIN DoubleDQN consistently outperforms the standard DoubleDQN, demonstrating improved sample efficiency and ultimately higher scores.
This figure shows the learning performance of CHAIN PPO on four MuJoCo tasks. It also displays the conventional PPO policy loss and the regularization loss during learning, in addition to showing how CHAIN reduces policy churn. The results indicate improved performance from CHAIN, particularly in Ant-v4 and HalfCheetah-v4.

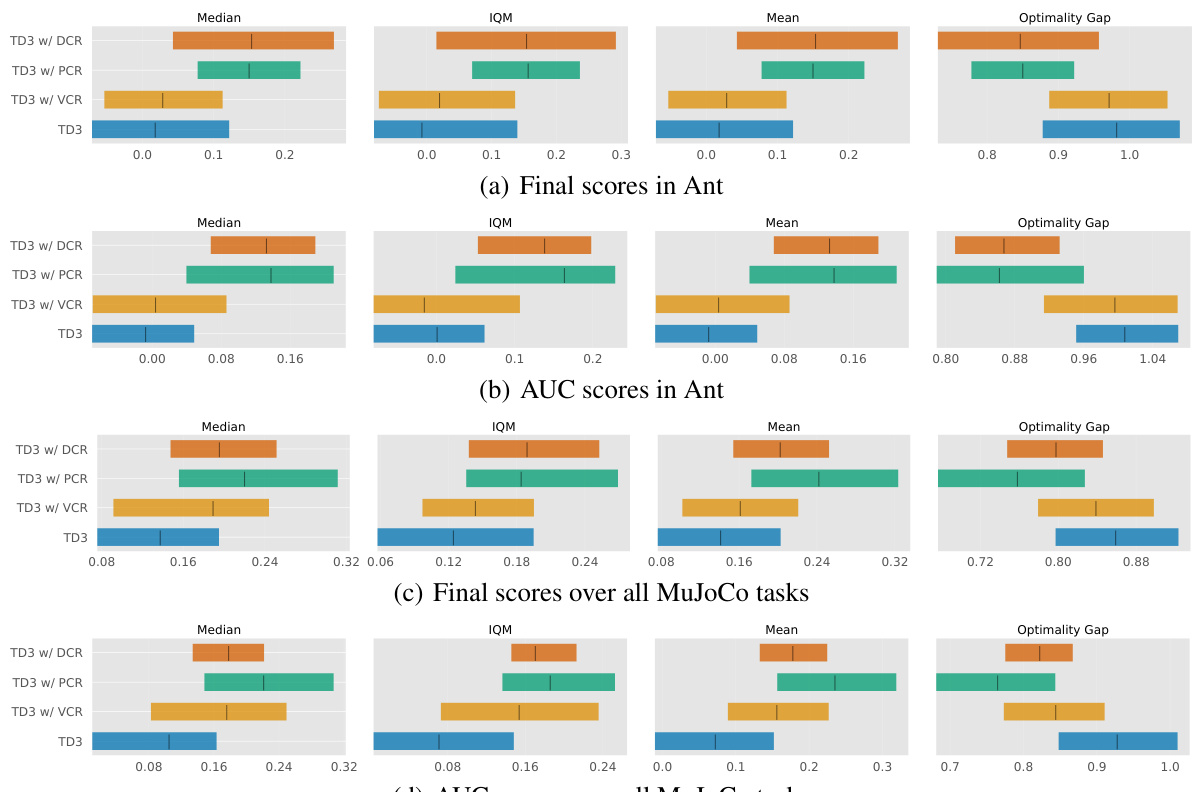
This figure compares the performance of TD3 with different churn reduction methods (VCR, PCR, DCR) using Reliable metrics proposed by Agarwal et al. (2021). The metrics shown (Median, IQR, Mean, Optimality Gap) are used to assess the quality of the policy learned by each method. The comparison is done for the Ant environment and across all MuJoCo environments, providing a comprehensive evaluation of the various churn reduction techniques on the TD3 algorithm.

This figure shows the learning curves of CHAIN DoubleDQN and regular DoubleDQN on six different games from the MinAtar environment. The y-axis represents the episode return (reward accumulated over an episode), while the x-axis shows the number of timesteps. The lines represent the average performance across six independent runs, and the shaded areas represent the standard error of the mean. The results demonstrate that CHAIN DoubleDQN consistently outperforms regular DoubleDQN across various games, indicating improved sample efficiency and final performance.
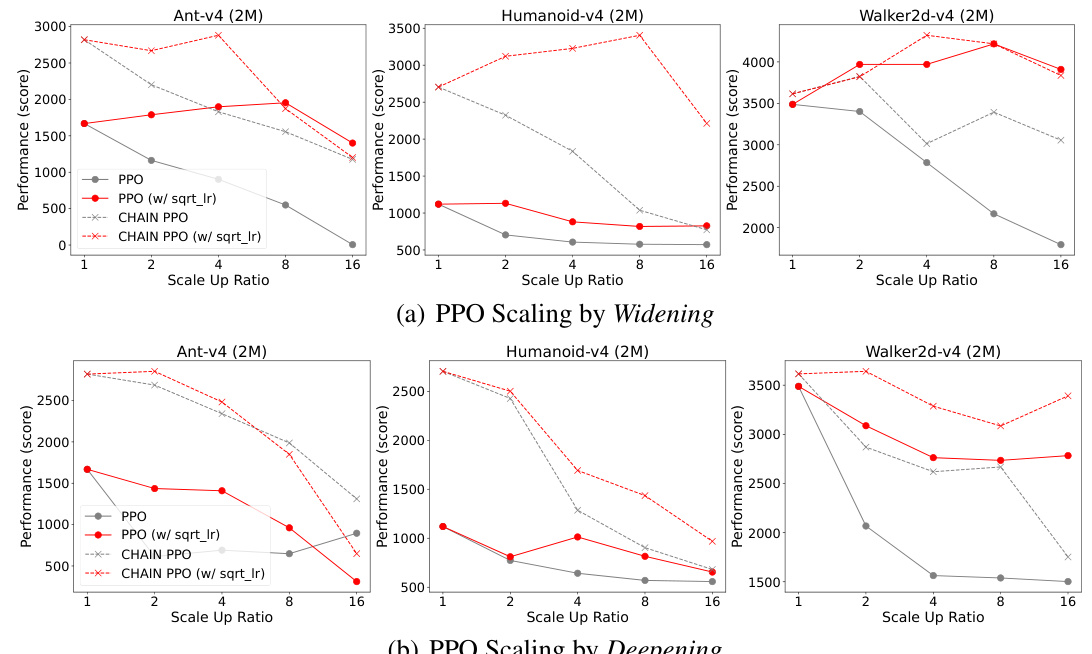
This figure shows the results of scaling up PPO by widening the network layers. The x-axis represents the scale-up ratio, while the y-axis represents the episode return. The lines in gray represent the performance of standard PPO under different scaling ratios and learning rates. The red lines show the improved performance of PPO when a reduced learning rate is used (sqrt of the scale-up ratio). The dashed lines show the results achieved using CHAIN PPO. CHAIN PPO demonstrates a significant improvement in performance across different scaling ratios and learning rates, highlighting its effectiveness in enhancing the scalability of PPO.
More on tables

This table presents the results of the CHAIN AWAC algorithm on the Adroit benchmark. It shows the mean and standard error of the performance (likely a success metric) for the AWAC algorithm, CHAIN AWAC using Policy Churn Reduction (PCR), and CHAIN AWAC using Value Churn Reduction (VCR), each evaluated over twelve random seeds. The results demonstrate the improvement in performance achieved by using CHAIN, specifically the PCR variant.
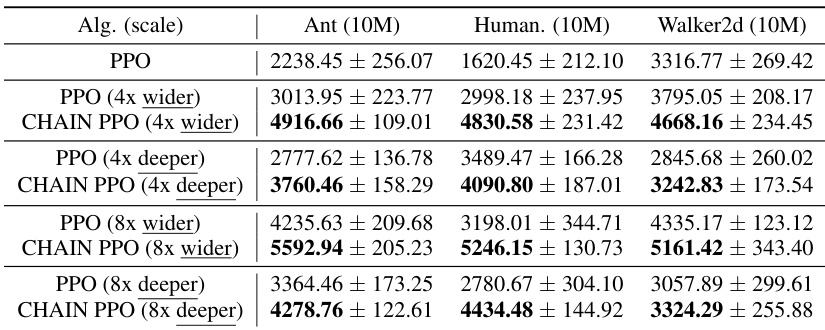
This table presents the results of scaling experiments using Proximal Policy Optimization (PPO) with and without the CHAIN method. It shows the mean and standard error of the final episode return across six random seeds for different network scaling configurations (wider and deeper networks) and for both standard PPO and PPO with CHAIN. The results demonstrate the impact of CHAIN on the scaling performance of PPO in various scenarios, particularly for larger network sizes.

This table presents the metrics used to quantify the value and policy churn in the experiments described in the paper. It breaks down the metrics into two categories: policy-based methods (like TD3, SAC, and PPO) and value-based methods (like DQN). For policy-based methods, the metrics include the value churn at a specific state-action pair, the overall value churn, the policy churn (measured using either L1 norm or KL divergence), and the deviation in the Q-value due to the change in policy. For value-based methods, the metrics measure the average Q-value change, the change in the maximum Q-value, and the deviation in greedy action selection.

This table lists the hyperparameters used for the DoubleDQN algorithm in the MinAtar environments. It shows both the standard hyperparameters for DoubleDQN (learning rate, training interval, discount factor, etc.) and the hyperparameters specific to the CHAIN method for reducing value churn (value regularization coefficient and target relative loss for automatic lambda adjustment). The conventional hyperparameter values are based on the recommendations in the cited paper by Young and Tian (2019).

This table lists the hyperparameters used for TD3 and SAC algorithms in the MuJoCo environments. It shows both the standard hyperparameters for each algorithm (taken from CleanRL, a publicly available implementation) and those specific to the CHAIN method (Churn Approximated Reduction) for value and policy churn reduction. The table is crucial for reproducing the experiments detailed in the paper and for understanding how the CHAIN method affects algorithm performance.

This table lists the hyperparameters used for TD3 and SAC algorithms in the MuJoCo environments. It includes learning rates for actor and critic networks, training intervals, exploration and target action noise parameters, discount factor, soft replacement ratio, initial random steps, replay buffer size, batch size, optimizer, and churn reduction hyperparameters. The table specifies the values used for both algorithms and highlights the differences where applicable. The churn reduction hyperparameters are further elaborated upon in the paper’s figures 6, 11, and 12.
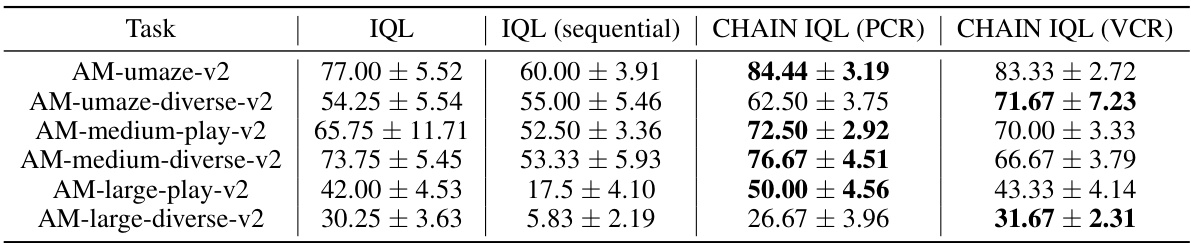
This table presents the results of three different methods on six Antmaze tasks from the D4RL benchmark. The methods compared are IQL (the standard iterative training method), IQL (sequential) which trains the value network first, and then the policy network with the frozen value network, and CHAIN IQL (with both PCR and VCR variants) which incorporates the proposed churn reduction method. The table shows the mean ± standard error of the final scores achieved by each method on each task over twelve random seeds. The results are intended to show the effectiveness of CHAIN IQL in improving the final performance of IQL across the Antmaze tasks.

This table presents the mean final episode returns of TD3 and DDQN agents across six random seeds in four different MinAtar environments (Walker2d, Ant, Asterix, Freeway). It compares the performance under different learning rates (lr) and target network replacement rates (trr). The results show how changing the learning rate and the target network update frequency affect the performance. The lr and trr values are modified by dividing or multiplying by factors of 2, 5, or 10.
Full paper#