TL;DR#
Reinforcement learning from human feedback (RLHF) is vital for aligning AI systems with human preferences, but human annotators often provide inconsistent or incorrect labels due to various factors such as bias, ambiguity, or lack of training. This unreliability significantly hinders the performance and robustness of RLHF systems. Existing methods are often limited in addressing this critical challenge.
This paper introduces R³M, a robust RLHF approach that models unreliable labels as sparse outliers. It uses an l1-regularized maximum likelihood estimation method and an efficient alternating optimization algorithm to learn a robust reward model while identifying and mitigating the impact of these outliers. Experiments on robotic control and natural language generation demonstrate R³M’s superior robustness and performance compared to standard RLHF methods, especially in scenarios with significant label corruption. R³M’s versatility allows for extensions to various preference optimization methods, further enhancing its applicability and impact.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in reinforcement learning and AI alignment because it directly tackles the problem of unreliable human feedback, a major bottleneck in current RLHF approaches. The proposed method, R³M, offers a novel and practical solution to improve the robustness and reliability of reward models by treating inconsistent feedback as sparse outliers. This work opens up new avenues for robust RLHF and will likely influence future research directions in AI safety and alignment.
Visual Insights#
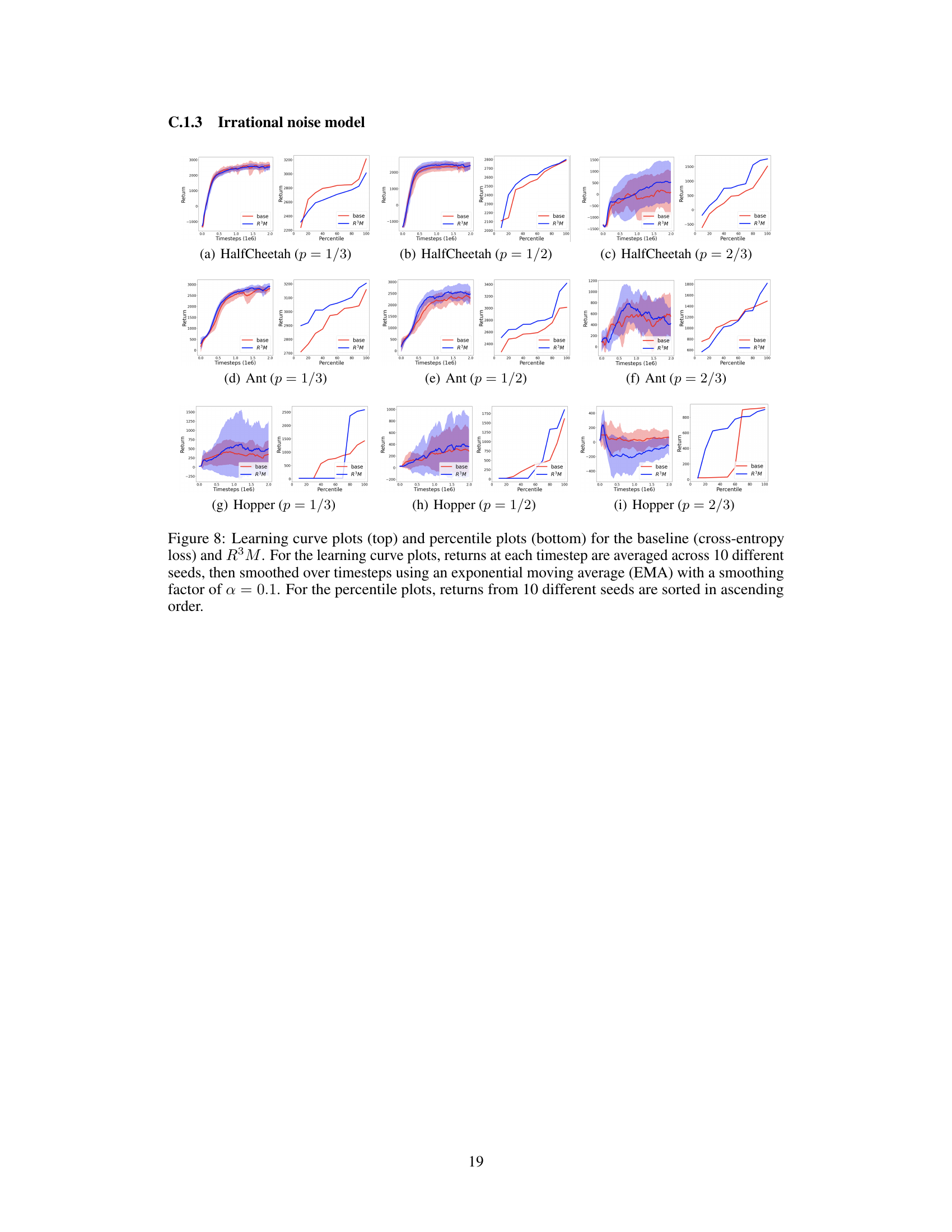
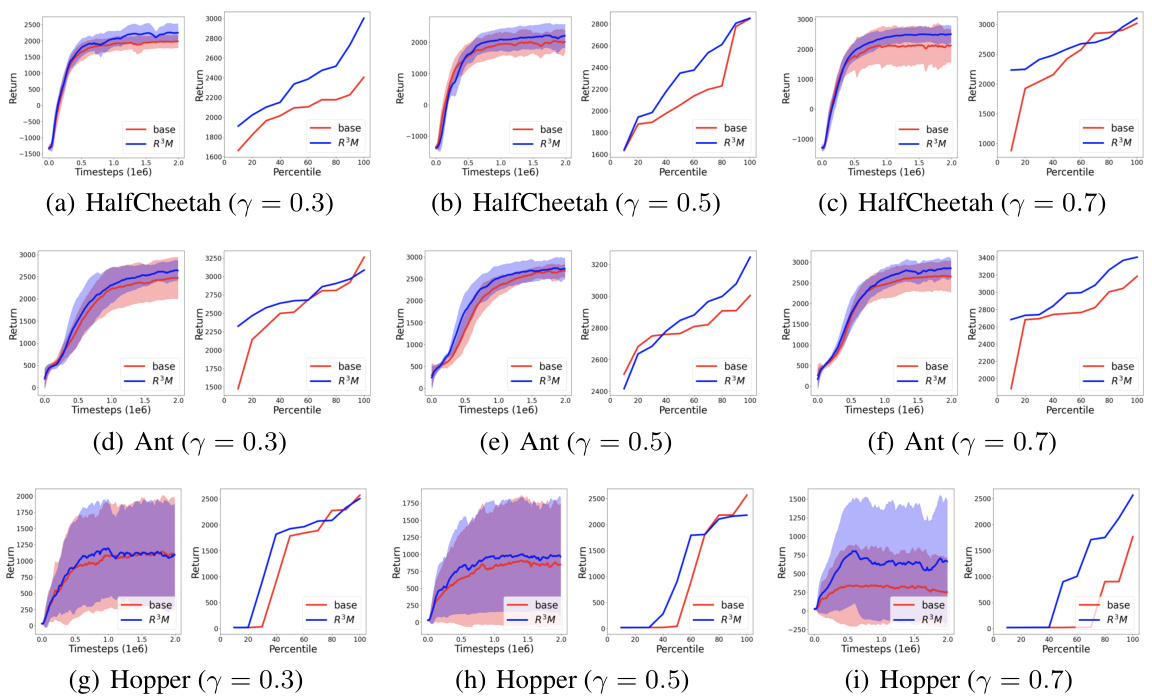
🔼 This figure presents the normalized returns for both the baseline (cross-entropy loss) and the proposed R³M method across three different robotic control tasks under various noise models and noise rates. The normalized returns are calculated relative to the average returns obtained using the ground truth reward. Error bars show standard deviation across ten different random seeds, indicating the variability of results. The figure shows R³M consistently outperforms the baseline under most scenarios. More detailed results (learning curves and percentile plots) are available in Appendix C.1.
read the caption
Figure 1: Normalized returns for the baseline (cross-entropy loss) and R³M across all noise models and noise rates. Error bars represent the standard deviation across 10 different seeds. Learning curves and percentile plots are in Appendix C.1.

🔼 This table presents the results of different preference optimization methods (SLIC-HF, IPO, Data Filtering, DPO, and R3M-DPO) on two natural language generation tasks: dialogue and summarization. For each method and task, the table shows the win rate (percentage of times the method’s generated response was preferred over the reference model) and the winning score (a normalized measure of the win rate). The confidence intervals reflect the variability across three different random seeds used during evaluation.
read the caption
Table 1: Win rates and winning scores for dialogue and summarization tasks. Confidence intervals are over three seeds.
In-depth insights#
Robust RLHF#
Robust Reinforcement Learning from Human Feedback (RLHF) addresses a critical challenge in aligning AI systems with human preferences: the unreliability of human feedback. Standard RLHF methods are vulnerable to noisy, inconsistent, or even malicious preference labels, leading to poorly aligned AI systems. Robust RLHF tackles this by incorporating techniques that enhance the resilience of the reward learning process to such corruptions. This might involve modeling noisy labels as outliers, employing robust statistical methods for reward estimation, or designing reward functions less sensitive to individual preference variations. The core aim is to develop algorithms that consistently learn accurate reward models even in the presence of significant data imperfections, ultimately leading to more reliable and robust AI systems aligned with human values.
R3M Algorithm#
The core of the research paper revolves around the proposed R3M algorithm, a robust method for reward modeling in reinforcement learning from human feedback (RLHF). R3M tackles the challenge of corrupted human preference labels, a prevalent issue in RLHF stemming from annotator biases or inconsistencies. Instead of discarding or smoothing noisy labels, R3M models these corruptions as sparse outliers, leveraging an l1-regularized maximum likelihood estimation to learn a robust reward model. This approach is computationally efficient, adding negligible overhead compared to standard RLHF. Theoretical analysis guarantees the algorithm’s consistency, provided that the number of outlier labels scales sublinearly with the dataset size. Moreover, R3M’s versatility is showcased through its successful extension to various preference optimization methods such as direct preference optimization (DPO), and its effectiveness is experimentally validated across diverse tasks including robotic control and natural language generation, consistently outperforming standard methods in the presence of label corruption.
Outlier Modeling#
Outlier modeling in the context of reinforcement learning from human feedback (RLHF) is crucial because human preferences are inherently noisy and susceptible to errors. The core idea is to identify and mitigate the influence of these outliers during reward model training, thus improving the robustness of the learned reward function and preventing the model from learning suboptimal or unsafe behaviors. Several approaches are possible: explicitly modeling outliers as a separate component in the reward function or using robust statistical methods that are less sensitive to extreme values. Regularization techniques can also help in reducing the sensitivity to outliers by penalizing complex reward models. The choice of outlier modeling method depends on the specific assumptions about the nature and characteristics of outliers in the dataset. Evaluating the effectiveness of outlier modeling techniques requires careful consideration of metrics beyond standard performance measures. It’s important to assess the generalization ability of the model to unseen data points and also evaluate its resistance to different types of noisy or malicious feedback.
Empirical Results#
A strong ‘Empirical Results’ section would thoroughly evaluate the proposed R3M method against baselines, using diverse and challenging scenarios. Quantitative metrics such as normalized returns (for robotics), win rates, and winning scores (for language generation) should be meticulously reported, accompanied by error bars or confidence intervals to demonstrate statistical significance. The section should systematically vary experimental parameters, such as the noise level or type, to showcase the robustness and generalizability of R3M across different conditions. Visualization through learning curves, percentile plots, and perhaps heatmaps would effectively convey the performance trends and comparisons, offering valuable insights into the effectiveness of R3M under various levels of data corruption. Furthermore, ablation studies testing the impact of key components of the R3M method would validate design choices and highlight the contributions of each part. Finally, a discussion interpreting the results in light of the theoretical findings, addressing any discrepancies or unexpected observations, would strengthen the overall impact of the section.
Future Work#
Future research directions stemming from this work on robust reinforcement learning from corrupted human feedback could explore several promising avenues. Extending the R³M framework to handle more complex types of corruption, beyond the deterministic outliers considered here, is crucial. This includes investigating robustness to stochastic noise and adversarial attacks on the preference labels. Further theoretical analysis focusing on the convergence rates under various corruption models and sample complexity would strengthen the theoretical underpinnings. Empirically, scaling R³M to even larger language models and more complex robotic control tasks is important. Investigating the interaction between the sparsity of the corruption and the complexity of the reward model would provide further insight into the effectiveness of R³M. Finally, exploring applications in other domains such as personalized medicine, education, and other human-in-the-loop AI systems, where corrupted feedback is prevalent, could demonstrate the broad applicability and impact of this robust RLHF method. Furthermore, studying the trade-off between robustness and efficiency in different scenarios will pave the way for more practical and reliable RLHF approaches. Robust reward modeling should be tested in safety-critical applications and evaluated for its ability to mitigate risks due to feedback errors.
More visual insights#
More on figures

🔼 This figure shows the results of comparing Claude 3’s agreement with human annotators on labels for two datasets: summarization and dialogue. Panel (a) is a bar chart showing that Claude 3 agrees more with human annotators when the learned perturbation factor (delta) is zero (no outlier). Panel (b) shows an example from the HH dataset where an annotator gives a positive label to a response that is clearly unhelpful or harmful, demonstrating a corrupted annotation. This helps illustrate how the model identifies and handles outliers in the preference data.
read the caption
Figure 2: (a) Comparison of the Claude 3 agreement on the annotated labels between sample pairs with zero and positive learned perturbation factors. (b) An example of corrupted annotation in the HH dataset.
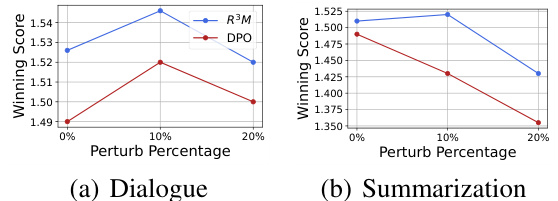
🔼 This figure compares the performance of R³M and DPO on dialogue and summarization tasks with varying levels of manually introduced label noise (perturbation). The x-axis represents the percentage of labels that were flipped. The y-axis shows the winning score, a metric reflecting the models’ performance relative to a baseline. The results demonstrate R³M’s superior robustness to noisy labels across both tasks, particularly in the summarization task.
read the caption
Figure 3: Comparison of winning scores between R³M and the DPO baseline across different perturbation percentages on two tasks.

🔼 The figure shows the normalized returns for three different robotic control tasks (HalfCheetah, Ant, and Hopper) under three different noise models (stochastic, myopic, and irrational) with varying noise rates. The baseline uses a standard cross-entropy loss, while R³M is the proposed robust reward modeling approach. The results demonstrate the superior performance of R³M across all tasks, noise models, and noise rates, especially in high noise scenarios. Error bars show standard deviation, and more detailed learning curves and percentile plots are provided in Appendix C.1.
read the caption
Figure 1: Normalized returns for the baseline (cross-entropy loss) and R³M across all noise models and noise rates. Error bars represent the standard deviation across 10 different seeds. Learning curves and percentile plots are in Appendix C.1.

🔼 This figure compares the performance of the proposed R³M method against a baseline (cross-entropy loss) across three robotic control tasks (HalfCheetah, Ant, and Hopper) under different noise models (stochastic, myopic, and irrational) with varying noise levels. The normalized returns are plotted, showing R³M’s consistent outperformance across various noise conditions, with error bars illustrating the standard deviation across multiple trials. Appendix C.1 provides more detailed learning curves and percentile plots.
read the caption
Figure 1: Normalized returns for the baseline (cross-entropy loss) and R³M across all noise models and noise rates. Error bars represent the standard deviation across 10 different seeds. Learning curves and percentile plots are in Appendix C.1.

🔼 The figure compares the performance of the proposed robust reward modeling method (R³M) against a baseline method (cross-entropy loss) across three different robotic control tasks under various noise conditions. The noise is simulated using three different models: stochastic, myopic, and irrational, each with varying noise rates. The normalized returns are plotted, with error bars indicating the standard deviation across multiple trials. Additional learning curves and percentile plots are available in the appendix.
read the caption
Figure 1: Normalized returns for the baseline (cross-entropy loss) and R³M across all noise models and noise rates. Error bars represent the standard deviation across 10 different seeds. Learning curves and percentile plots are in Appendix C.1.
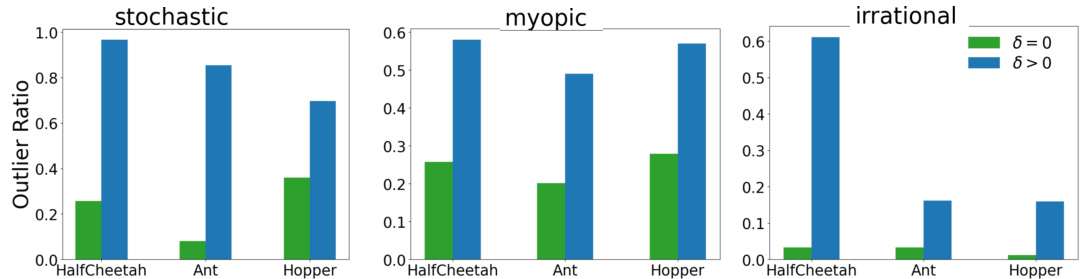
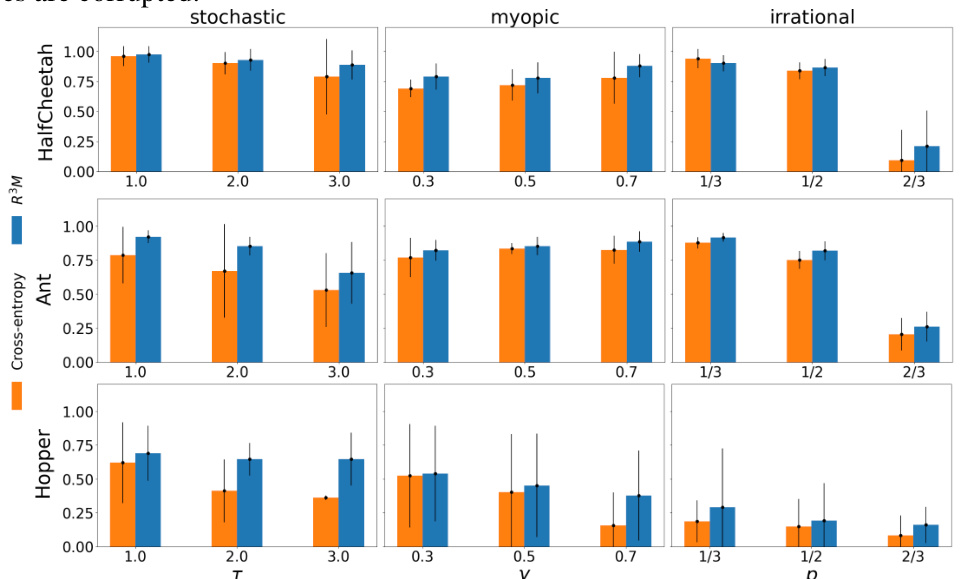
🔼 This figure compares the outlier ratios for three different noise models (stochastic, myopic, and irrational) in robotic control experiments. It shows the proportion of outlier data points identified by the R³M algorithm, categorized by whether the learned perturbation factor (δ) is zero or positive. A higher ratio of positive δ indicates a greater number of outliers successfully identified by the method.
read the caption
Figure 5: Comparison of outlier ratios between sample pairs with zero and positive learned perturbation factors for τ = 1.0, γ = 0.3, and p = 1/3 for the stochastic, myopic, and irrational noise models, respectively

🔼 This figure compares the performance of the proposed R³M method against a baseline (cross-entropy loss) across three robotic control tasks under various noise models (stochastic, myopic, and irrational) and noise levels. The normalized returns, representing the average performance relative to the ground truth reward, are shown for each task and noise condition. Error bars illustrate the standard deviation across multiple runs (10 seeds). More detailed learning curves and percentile plots are available in Appendix C.1 for a comprehensive analysis.
read the caption
Figure 1: Normalized returns for the baseline (cross-entropy loss) and R³M across all noise models and noise rates. Error bars represent the standard deviation across 10 different seeds. Learning curves and percentile plots are in Appendix C.1.
🔼 This figure displays the normalized returns achieved by the baseline model (using cross-entropy loss) and the proposed R³M model across three different robotic control tasks (HalfCheetah, Ant, and Hopper) under various noise conditions. Three types of noise models were applied to the preference data: stochastic, myopic, and irrational, each with varying noise rates. The results are presented for each task and noise model separately. Error bars show the standard deviation across 10 runs for each condition, illustrating the variability in performance. Additional learning curves and percentile plots providing a more detailed performance analysis are available in Appendix C.1 of the paper.
read the caption
Figure 1: Normalized returns for the baseline (cross-entropy loss) and R³M across all noise models and noise rates. Error bars represent the standard deviation across 10 different seeds. Learning curves and percentile plots are in Appendix C.1.

🔼 The figure displays the performance comparison between the baseline model (using cross-entropy loss) and the proposed R³M model across three different robotic control tasks (HalfCheetah, Ant, and Hopper) under various noise conditions (stochastic, myopic, and irrational). Each noise model simulates different types of human preference label corruption with varying noise rates (controlled by parameters τ, γ, and p respectively). The normalized returns of each model under each noise condition are shown, with error bars representing the standard deviation across ten trials. Appendix C.1 provides additional details like learning curves and percentile plots.
read the caption
Figure 1: Normalized returns for the baseline (cross-entropy loss) and R³M across all noise models and noise rates. Error bars represent the standard deviation across 10 different seeds. Learning curves and percentile plots are in Appendix C.1.
Full paper#