↗ arXiv ↗ Hugging Face ↗ Hugging Face ↗ Chat
TL;DR#
The increasing use of Large Language Models (LLMs) in diverse applications necessitates efficient methods for deploying multiple models. Existing approaches like low-rank and low-bit compression often compromise performance, especially for task-specific fine-tuned LLMs. This issue is exacerbated in resource-constrained environments like multi-tenant serving, where multiple LLMs are needed to meet complex demands.
This paper introduces Delta-CoMe, a training-free delta compression method that employs mixed-precision quantization. It assigns higher-bit representation for significant singular vectors in delta weights, improving approximation accuracy. Results show Delta-CoMe surpasses low-rank and low-bit baselines across various LLMs (math, code, chat, and multi-modal), achieving comparable performance to full fine-tuned models with over 10x savings in GPU memory and disk storage. The compatibility with various LLMs like Llama-2, Llama-3, and Mistral highlights its generalizability and practical significance.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the efficiency challenges in deploying multiple large language models (LLMs) by introducing a novel training-free delta compression method called Delta-CoMe. Delta-CoMe significantly improves upon existing methods by employing mixed-precision quantization, achieving comparable performance to full fine-tuned LLMs while reducing storage and computational costs. This is crucial for resource-constrained applications and multi-tenant serving scenarios, opening new avenues for research in efficient LLM deployment and management. The generalizability across various LLMs (Llama-2, Llama-3, Mistral) further broadens its potential impact.
Visual Insights#
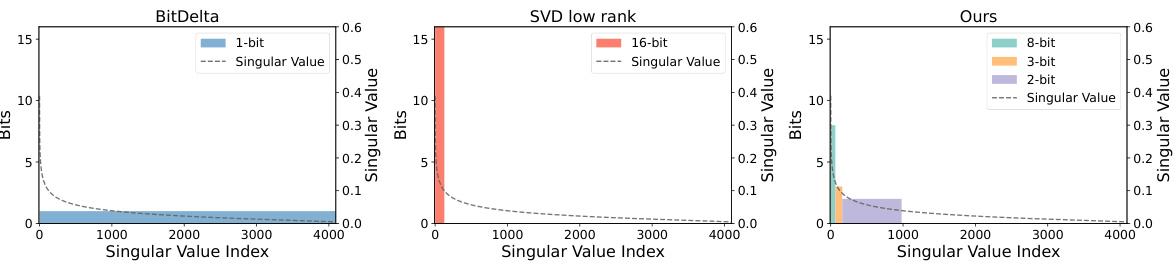
🔼 This figure compares three different delta compression methods: BitDelta, SVD low rank, and the proposed Delta-CoMe. Each subfigure shows the distribution of bits used to quantize singular vectors against their corresponding singular values. BitDelta uses 1 bit for all singular vectors. SVD low rank retains only the top k singular values and vectors, discarding the rest. Delta-CoMe uses a mixed-precision approach, allocating more bits to the singular vectors with larger singular values and fewer bits to those with smaller singular values, reflecting the long-tail distribution observed in delta weights.
read the caption
Figure 1: Left: illustration of BitDelta (Liu et al., 2024b), which employs 1-bit quantization for all the delta weights. Middle: illustration of low-rank compression (Ryu et al., 2023b), retaining the top-k singular values and the corresponding singular vectors. Right: illustration of the proposed Delta-CoMe method, which represents the singular vectors of larger singular values using high-bit vectors while compressing the singular vectors of smaller singular values into low-bit representations. This method is inspired by the long-tail distribution of singular values in delta weights.
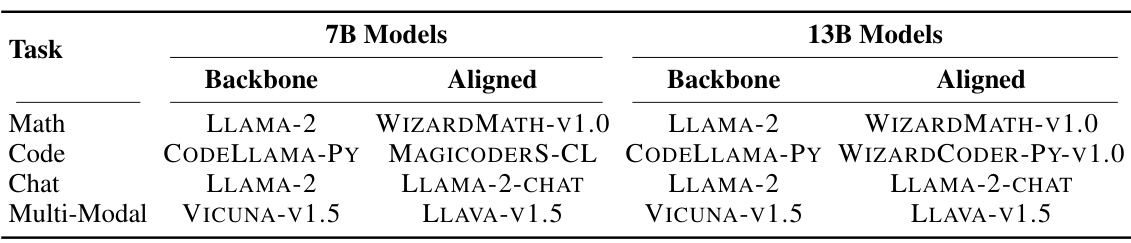
🔼 This table lists the backbone and aligned large language models (LLMs) used in the paper’s experiments. For each of four tasks (Math, Code, Chat, Multi-Modal), it shows the base pre-trained LLM and the task-specific fine-tuned version of that model. Two sizes of models are included: 7B parameter models and 13B parameter models, reflecting different scales of model complexity.
read the caption
Table 1: Selected backbone and aligned models for the examined four tasks.
In-depth insights#
Mixed-Precision Quantization#
The concept of ‘Mixed-Precision Quantization’ in the context of compressing delta weights for large language models is a significant advancement in efficient model deployment. It leverages the observation that singular vectors associated with larger singular values contribute more significantly to the model’s performance. This insight allows for a more nuanced compression strategy, using higher bit-widths for these crucial vectors and lower bit-widths or even omitting those with negligible impact. The result is a compression method that balances model size reduction with minimal performance degradation. Mixed-precision quantization offers a superior alternative to uniform low-bit or low-rank approaches, which can severely impact the accuracy of task-specific fine-tuned LLMs. This approach demonstrates adaptability, proving compatible with diverse backbone models, and opens avenues for exploring the balance between precision levels and compression ratios to optimize resource usage and accuracy tradeoffs.
Delta Compression Methods#
Delta compression, a crucial technique for efficient large language model (LLM) deployment, focuses on compressing the difference (delta) between a base model and its fine-tuned variants. Low-rank methods approximate the delta weights using a lower-rank representation, reducing storage needs but potentially sacrificing accuracy. Low-bit quantization, conversely, reduces the precision of delta weights, resulting in smaller files but potentially impacting model performance. The paper explores a novel approach, employing mixed-precision quantization, which cleverly allocates higher bit-widths to singular vectors representing larger singular values in the delta weights. This strategic allocation balances compression with accuracy, achieving superior performance compared to pure low-rank or low-bit techniques. The effectiveness is demonstrated across diverse LLMs, including those specializing in math, code, chat, and even vision-language tasks, highlighting its generalizability and offering a promising direction for optimizing LLM deployment in resource-constrained environments.
LLM Compression#
Large Language Model (LLM) compression techniques are crucial for deploying and serving these massive models efficiently. Reducing the model size minimizes storage requirements and lowers the computational cost of inference, making LLMs accessible to devices with limited resources. The paper explores various compression methods, including low-rank approximation and quantization, both of which aim to reduce the number of parameters in the model without significantly compromising performance. However, a key challenge is to find a balance between compression and accuracy. Mixed-precision quantization, as suggested in the paper, presents a promising approach, using different precision levels for different components of the model to optimize both the size and the accuracy of the compressed model. This strategy is particularly effective when applied to the delta weights (the difference between a base model and a fine-tuned model), as these tend to have a long-tail distribution of singular values. The results highlight the effectiveness of this approach in achieving high compression ratios while maintaining accuracy comparable to the full model, thus making multi-model serving a more feasible and practical deployment strategy.
Multi-Model Serving#
Multi-model serving presents a significant challenge in deploying large language models (LLMs). Serving multiple LLMs simultaneously, each specialized for different tasks or user needs, increases efficiency and flexibility. However, this approach faces limitations in storage and computational resources. Delta-compression techniques address these issues by decomposing fine-tuned LLMs into a base model and delta weights, allowing for significant compression. Existing methods, like low-rank and low-bit compression, can hinder performance, especially for task-specific LLMs. Mixed-precision quantization, which assigns higher bit-widths to significant singular vectors in delta weights, offers a promising solution. This approach strikes a balance between compression and performance, demonstrated by outperforming previous methods in various LLM types and achieving comparable results to full fine-tuned models. This approach allows for efficient multi-model serving with reduced storage and computational costs, opening new avenues for deploying diverse and capable LLMs across diverse applications.
Future Work#
Future work for Delta-CoMe could explore several promising avenues. Extending the mixed-precision quantization to other model compression techniques beyond SVD would broaden its applicability and potentially improve performance further. Investigating different quantization methods and their impact on Delta-CoMe’s efficiency and accuracy is crucial. A comprehensive analysis of the trade-offs between compression ratio and accuracy across diverse LLMs and tasks is needed to define the optimal balance for specific applications. Furthermore, developing more efficient hardware acceleration of Delta-CoMe’s mixed-precision compression would significantly improve inference speed and reduce latency, which is particularly relevant in real-time scenarios. Finally, evaluating the robustness of Delta-CoMe against adversarial attacks and noisy inputs is critical for deploying it in production environments where security and reliability are paramount.
More visual insights#
More on figures
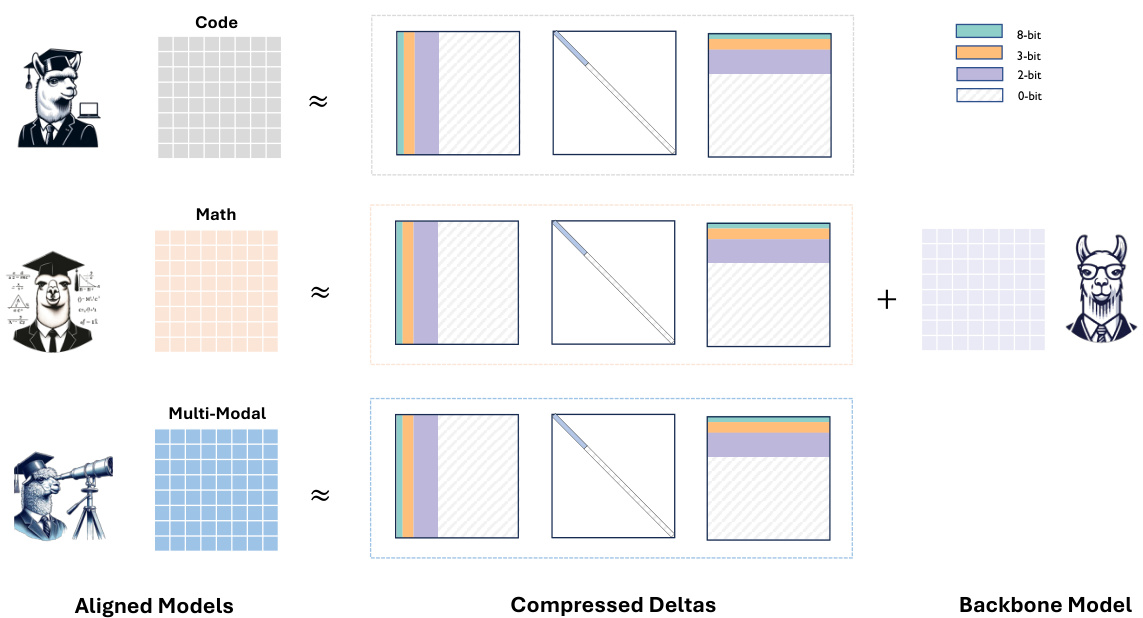
🔼 This figure illustrates the Delta-CoMe method. It shows how the method compresses delta weights between an aligned model and a backbone model by using different bit-widths for singular vectors based on their singular values. Larger singular values are represented with higher bit-widths (e.g., 8-bit), while smaller singular values use lower bit-widths (e.g., 3-bit, 2-bit), and the smallest are omitted (0-bit). This mixed-precision approach aims to achieve a balance between compression and accuracy. The figure visually shows this process for three different aligned models (Code, Math, and Multi-Modal).
read the caption
Figure 2: Illustration of Delta-CoMe, where we utilize varying bit-widths for singular vectors with different singular values. Singular vectors corresponding to larger singular values are assigned higher bit-widths. For extremely small singular values, we omit the singular vectors (i.e., 0-bit).
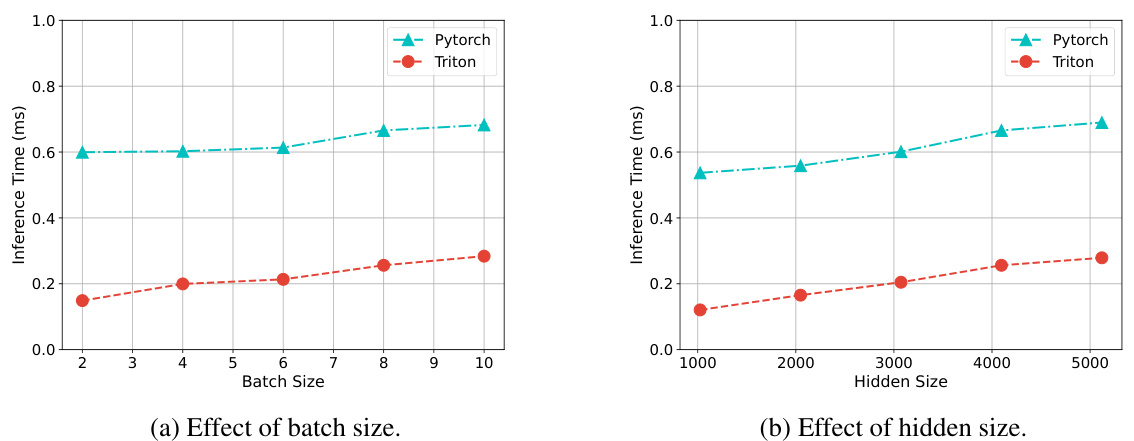
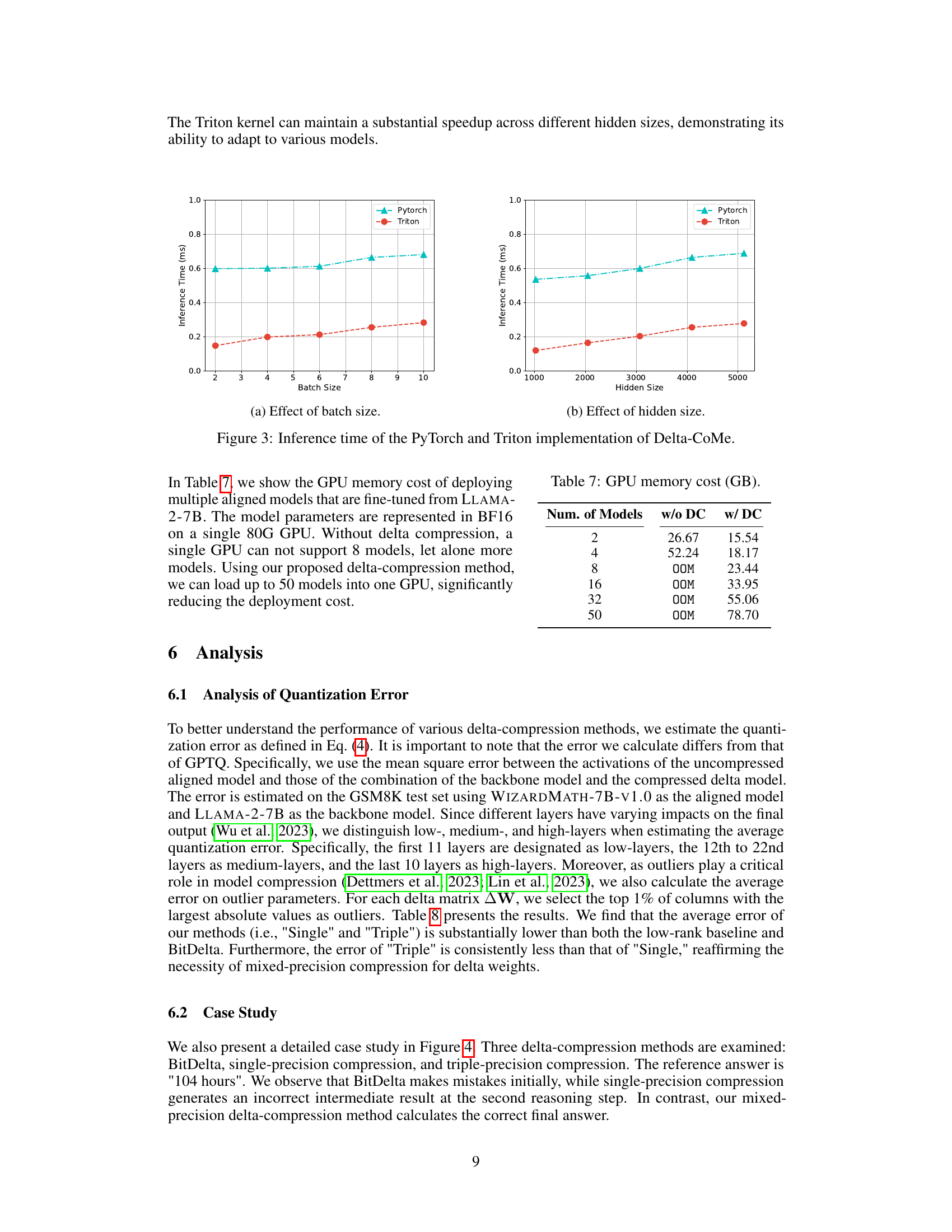
🔼 This figure shows the inference time comparison between PyTorch and Triton implementations of the Delta-CoMe model. The left subplot shows how inference time changes with varying batch sizes, while the right subplot demonstrates the impact of different hidden sizes on inference time. Both subplots show that the Triton implementation significantly outperforms the PyTorch implementation in terms of speed.
read the caption
Figure 3: Inference time of the PyTorch and Triton implementation of Delta-CoMe.

🔼 This figure compares three different delta compression methods: BitDelta, low-rank compression, and the proposed Delta-CoMe. It highlights how each method handles the singular values and vectors of the delta weights, showing BitDelta using 1-bit quantization, low-rank compression reducing the number of singular values, and Delta-CoMe using mixed-precision quantization based on the magnitude of the singular values. The long-tail distribution of singular values motivates the mixed-precision approach in Delta-CoMe.
read the caption
Figure 1: Left: illustration of BitDelta (Liu et al., 2024b), which employs 1-bit quantization for all the delta weights. Middle: illustration of low-rank compression (Ryu et al., 2023b), retaining the top-k singular values and the corresponding singular vectors. Right: illustration of the proposed Delta-CoMe method, which represents the singular vectors of larger singular values using high-bit vectors while compressing the singular vectors of smaller singular values into low-bit representations. This method is inspired by the long-tail distribution of singular values in delta weights.
More on tables
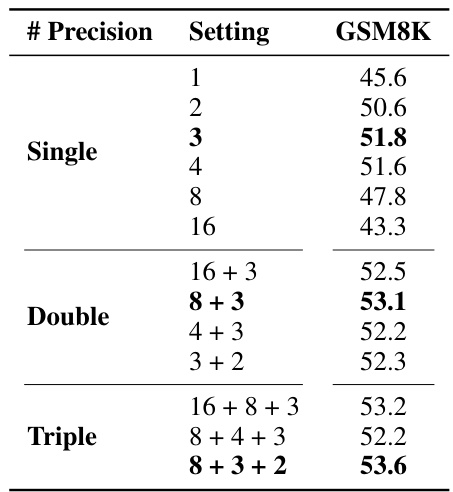
🔼 This table presents the results of an experiment comparing different mixed-precision strategies for compressing delta weights. The strategies are categorized as single, double, and triple precision, each with varying bit-width combinations for the singular vectors. The GSM8K score, a metric for mathematical problem-solving, is used to evaluate the performance of each strategy. The results show that mixed-precision strategies, particularly the triple-precision strategy (8+3+2), provide the best performance. This table highlights the impact of the bit-width allocation on the overall model performance and supports the choice of the 8+3+2 strategy for the Delta-CoMe method.
read the caption
Table 2: Comparison of different mixed-precision strategies.
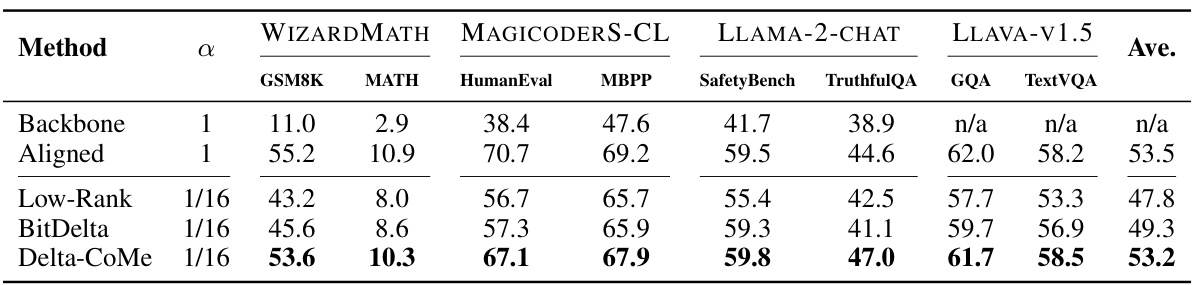
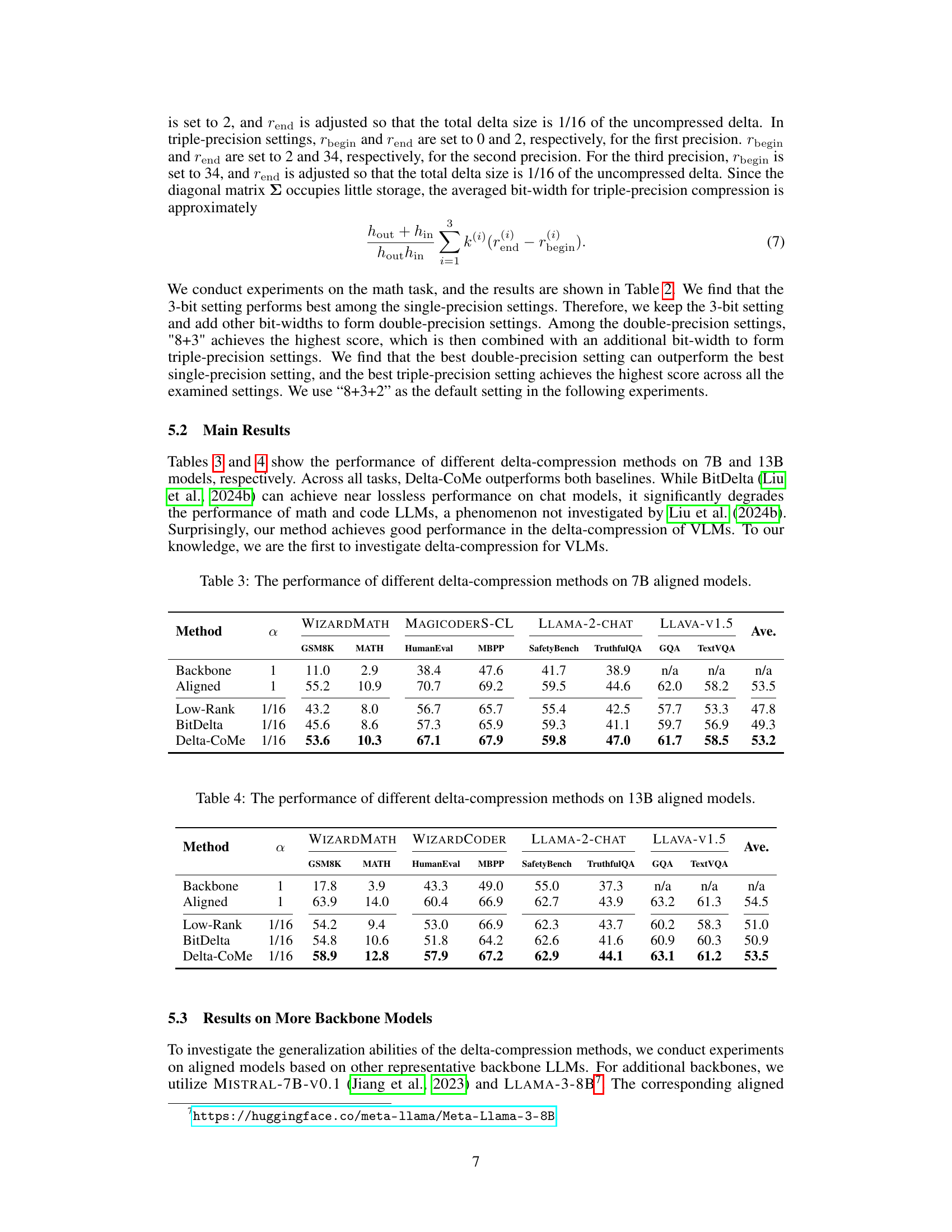
🔼 This table presents the performance comparison of different delta-compression methods (Low-Rank, BitDelta, and Delta-CoMe) against a baseline (Backbone) and a fully aligned model (Aligned) on 7B parameter aligned language models. The performance is evaluated across eight tasks: GSM8K, MATH, HumanEval, MBPP, SafetyBench, TruthfulQA, GQA, and TextVQA, representing mathematical reasoning, code generation, chat safety and helpfulness, and multi-modal capabilities, respectively. The ‘α’ column represents the compression ratio. The ‘Ave.’ column shows the average performance across all eight tasks.
read the caption
Table 3: The performance of different delta-compression methods on 7B aligned models.
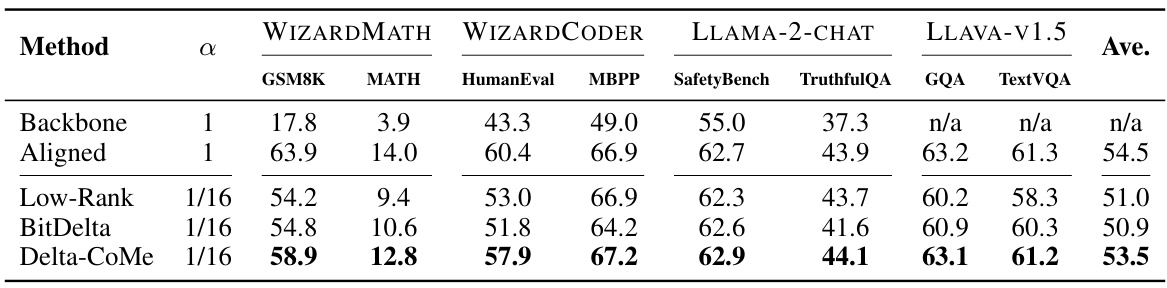
🔼 This table presents the performance comparison of different delta-compression methods (Low-Rank, BitDelta, and Delta-CoMe) against the baseline (Backbone and Aligned) on 13B parameter aligned models across various tasks: GSM8K (mathematics), HumanEval & MBPP (code generation), SafetyBench & TruthfulQA (chat), and GQA & TextVQA (multi-modal). The α column represents the compression ratio, showing how much smaller the compressed model is. The average performance across all tasks is also shown.
read the caption
Table 4: The performance of different delta-compression methods on 13B aligned models.

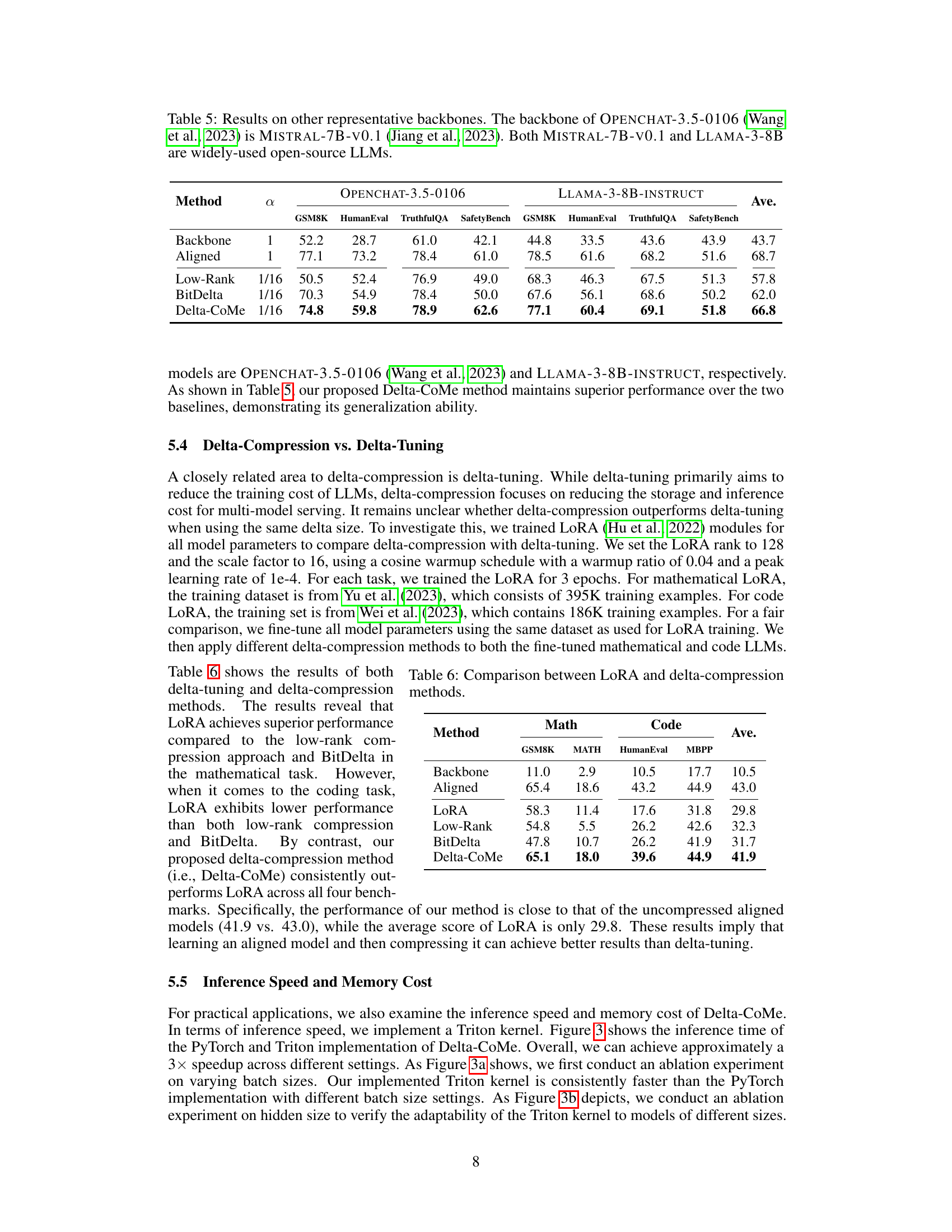
🔼 This table presents the performance of different delta-compression methods on two different open-source large language models: OPENCHAT-3.5-0106 and LLAMA-3-8B-INSTRUCT. The results are shown across four tasks (GSM8K, HumanEval, TruthfulQA, SafetyBench), and three delta compression methods (Low-Rank, BitDelta, Delta-CoMe) are compared with the full aligned model (Aligned) and the original backbone model (Backbone). The purpose is to demonstrate the generalization capabilities of the proposed Delta-CoMe approach to various backbone models.
read the caption
Table 5: Results on other representative backbones. The backbone of OPENCHAT-3.5-0106 (Wang et al., 2023) is MISTRAL-7B-v0.1 (Jiang et al., 2023). Both MISTRAL-7B-v0.1 and LLAMA-3-8B are widely-used open-source LLMs.
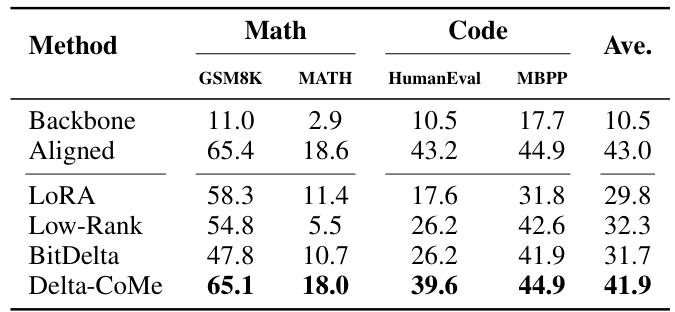
🔼 This table presents the performance comparison of various delta-compression methods (Low-Rank, BitDelta, and Delta-CoMe) against a baseline (Backbone) and a fully aligned model (Aligned) on four different tasks (GSM8K, MATH, HumanEval, MBPP) using 7B parameter models. The average performance across these tasks is also reported. The results showcase the effectiveness of Delta-CoMe in achieving performance comparable to the fully aligned models while significantly outperforming the baselines.
read the caption
Table 3: The performance of different delta-compression methods on 7B aligned models.
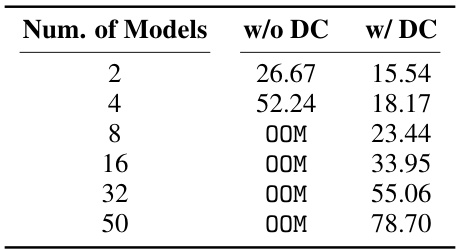
🔼 This table shows the GPU memory cost in GB for deploying multiple (2, 4, 8, 16, 32, 50) aligned models fine-tuned from LLAMA-2-7B with and without delta compression. The model parameters are represented in BF16 on a single 80G GPU. The table highlights that without delta compression (w/o DC), a single GPU cannot support more than 4 models, whereas with delta compression (w/ DC), up to 50 models can be loaded, demonstrating significant cost reduction.
read the caption
Table 7: GPU memory cost (GB).
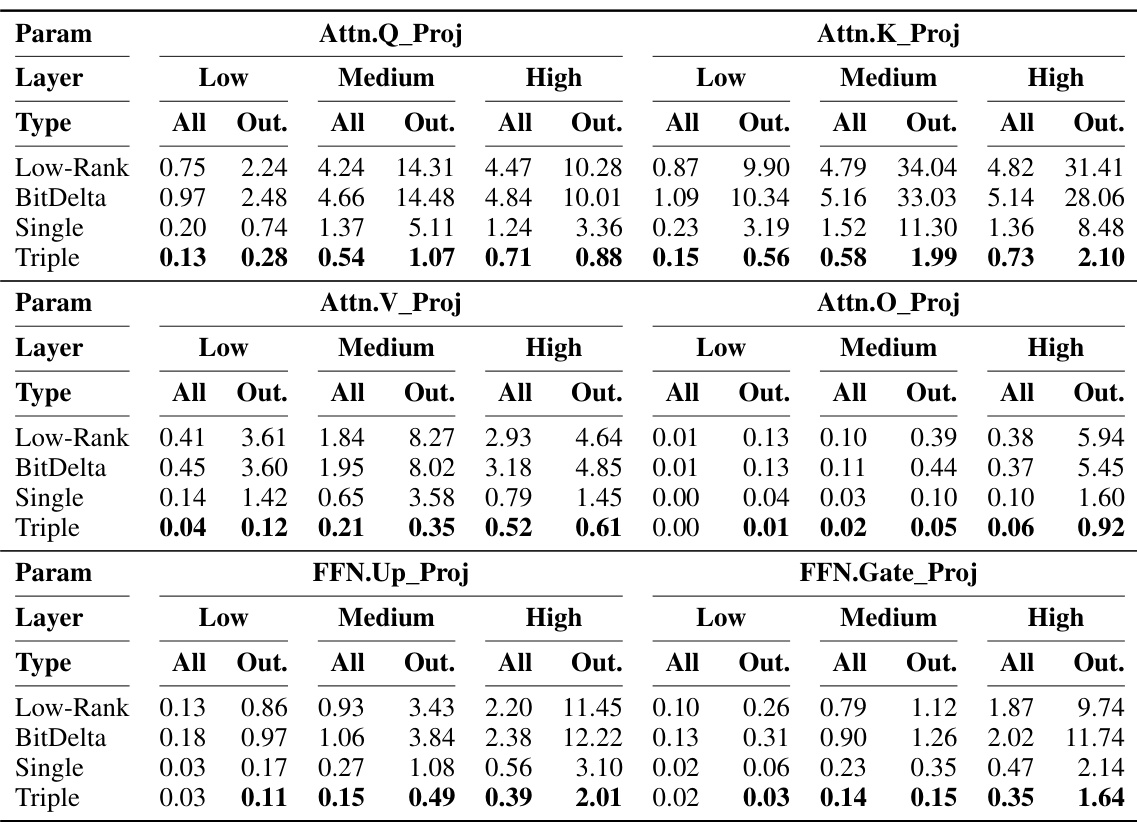
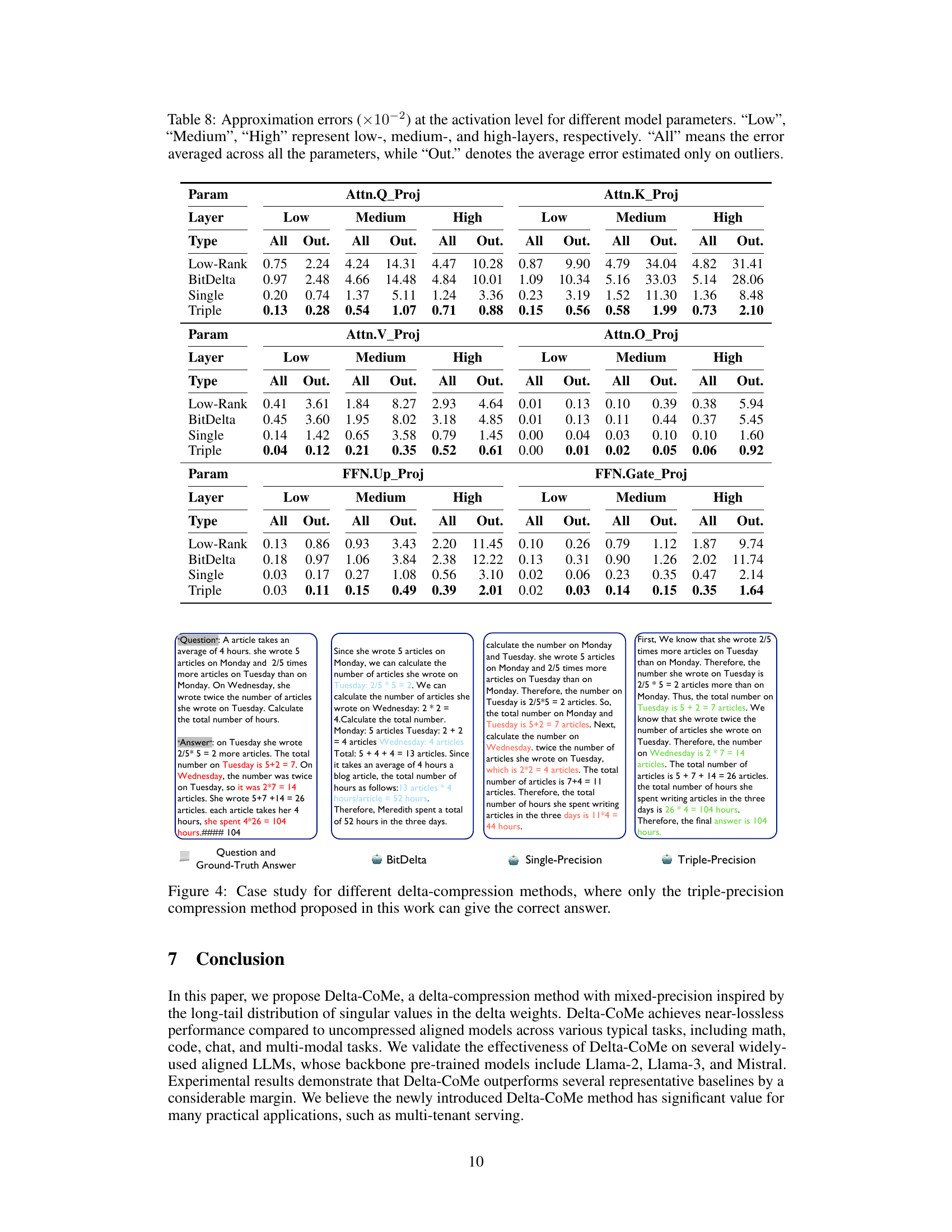
🔼 This table shows the approximation errors at the activation level for different model parameters in the low, medium, and high layers. It compares the errors for different methods: Low-Rank, BitDelta, Single, and Triple. The errors are calculated for all parameters and for outliers only. The table is useful for understanding the performance of different delta-compression methods.
read the caption
Table 8: Approximation errors (×10−2) at the activation level for different model parameters. “Low”, 'Medium”, 'High” represent low-, medium-, and high-layers, respectively. “All” means the error averaged across all the parameters, while “Out.” denotes the average error estimated only on outliers.
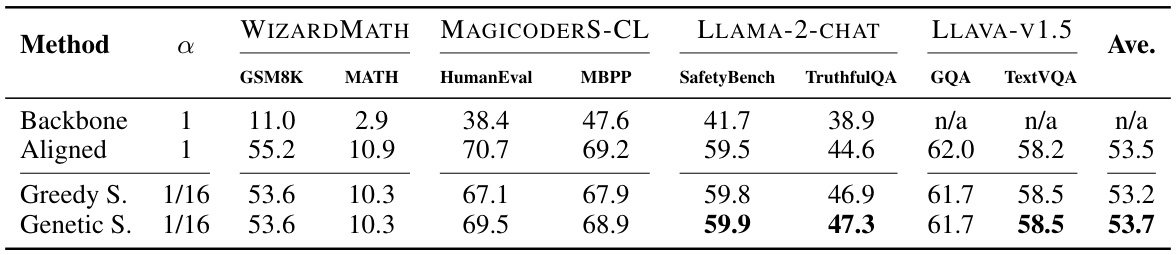
🔼 This table compares the performance of different bit allocation methods for delta compression on 7B aligned models. It shows the average scores across various tasks (GSM8K, MATH, HumanEval, MBPP, SafetyBench, TruthfulQA, GQA, TextVQA) for three methods: the original backbone model, a greedy search approach for bit allocation, and a genetic search approach. The greedy search uses a predefined strategy (detailed in Section 5.1), while the genetic search employs a genetic algorithm to optimize bit allocation. The table highlights that the genetic search, though computationally more expensive, provides better average performance than the greedy search and even surpasses the performance of the original half-precision models in some cases.
read the caption
Table 9: The performance of different bits allocate methods on 7B aligned models. “Greedy search” represents the method in Section 5.1.
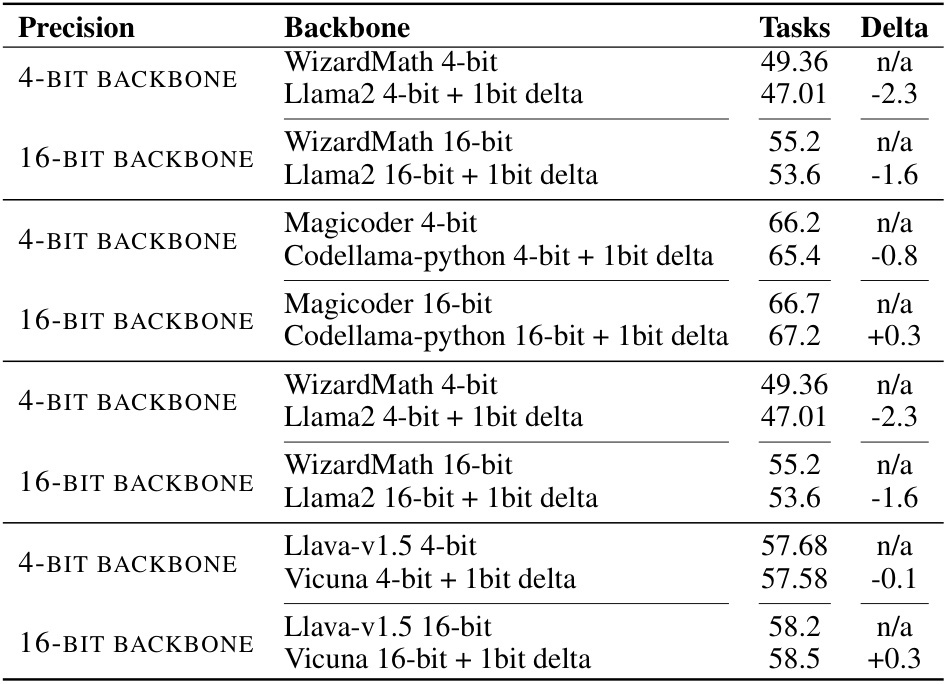
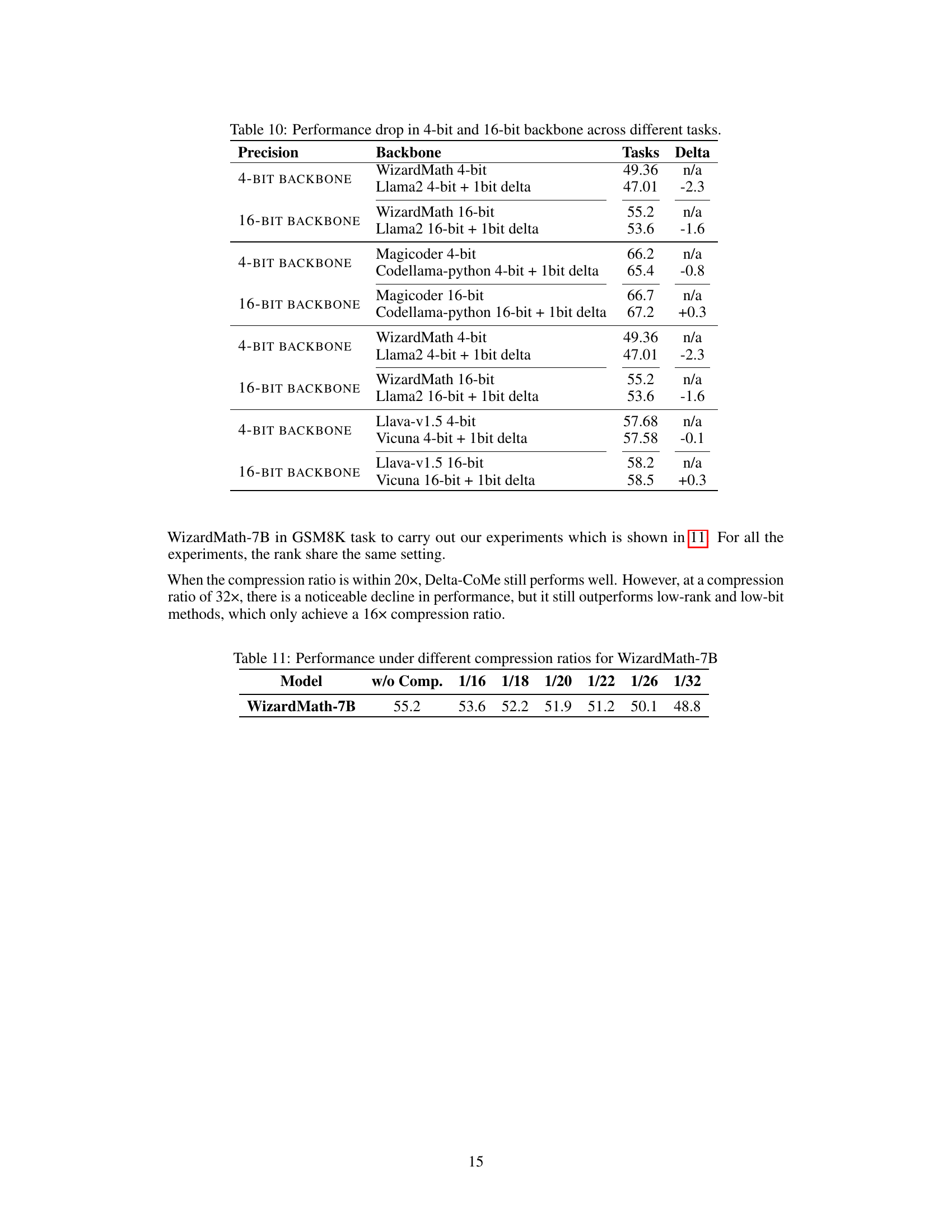
🔼 This table shows the performance drop when using 4-bit and 16-bit backbones with Delta-CoMe. It compares the performance with and without the 1-bit delta compression method, demonstrating that Delta-CoMe can maintain good performance even when using low-precision backbones.
read the caption
Table 10: Performance drop in 4-bit and 16-bit backbone across different tasks.

🔼 This table presents the performance of the WizardMath-7B model on the GSM8K task under various compression ratios achieved by Delta-CoMe. The ‘w/o Comp.’ column shows the performance without compression, serving as a baseline. The subsequent columns indicate performance with increasing compression levels (1/16, 1/18, 1/20, 1/22, 1/26, 1/32). The data illustrates how the model’s performance degrades gradually as the compression ratio increases. This table demonstrates the trade-off between compression level and performance.
read the caption
Table 11: Performance under different compression ratios for WizardMath-7B
Full paper#