↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Current diffusion models are slow due to their step-by-step denoising process. Many existing acceleration methods use a fixed approach, failing to account for the variability in the number of steps needed depending on the input prompt. This inefficiency hinders the use of diffusion models in real-time applications.
AdaptiveDiffusion tackles this issue by adaptively reducing the number of noise prediction steps based on the prompt’s characteristics. It does this using a novel third-order latent difference criterion to identify redundant steps. The results demonstrate significant speed improvements (up to 5.6x) across various models and tasks while maintaining identical output quality to full-step denoising. This prompt-adaptive acceleration paradigm is a significant step forward in making diffusion models more practical for interactive and real-time applications.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on diffusion models because it presents AdaptiveDiffusion, a novel method that significantly accelerates the denoising process without sacrificing image quality. This addresses a major limitation of current diffusion models, which are computationally expensive and slow. The method’s prompt-adaptive nature makes it particularly relevant for interactive applications. Furthermore, the theoretical analysis and empirical validation provide valuable insights for developing other efficient diffusion acceleration techniques.
Visual Insights#
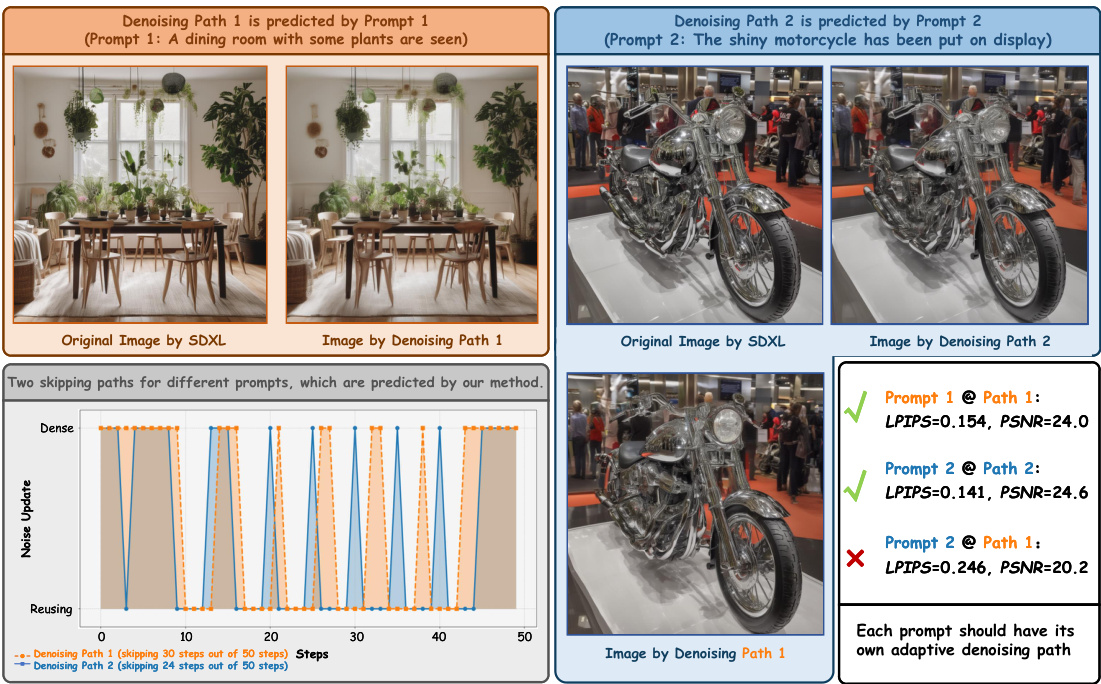
This figure compares the denoising paths for two different prompts using the Stable Diffusion XL model. It shows that the number of steps required to generate a high-quality image varies depending on the prompt. Prompt 1 requires fewer steps (20 out of 50) compared to Prompt 2 (26 out of 50), illustrating the need for a prompt-adaptive acceleration method.
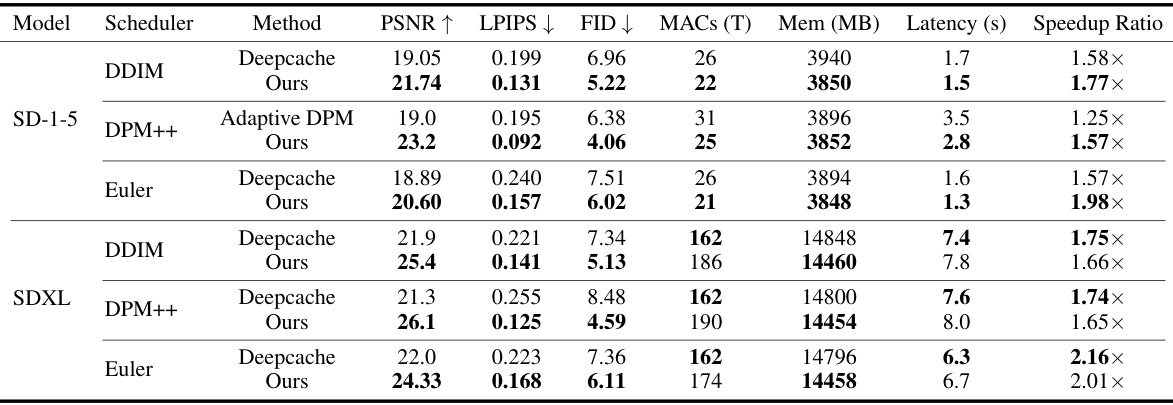
This table presents a quantitative comparison of different methods (Deepcache and AdaptiveDiffusion) on the MS-COCO 2017 dataset for image generation. Metrics such as PSNR, LPIPS, and FID are used to evaluate image quality. The table also shows MACs (Multiply-Accumulate operations), memory usage, latency, and speedup ratios, providing a comprehensive performance comparison of the different approaches across various sampling schedulers (DDIM, DPM++, Euler).
In-depth insights#
Adaptive Diffusion#
Adaptive diffusion methods represent a significant advancement in accelerating diffusion models, addressing the computational bottleneck inherent in traditional step-by-step denoising processes. Adaptive approaches are crucial because different prompts may require varying numbers of denoising steps to achieve high-quality results. The core idea is to intelligently skip redundant noise prediction steps based on a learned criterion or heuristic, optimizing efficiency without sacrificing image quality. This adaptive strategy contrasts with fixed acceleration methods which lack the flexibility to handle the nuances of diverse prompts. A key innovation often involves measuring the stability or redundancy between timesteps using latent difference metrics (e.g., third-order differences), guiding the selection of steps to skip. By leveraging these insights, adaptive methods achieve notable speedups (2-5x or even greater) across various image and video diffusion models, opening the door for real-time applications previously hindered by the computational demands of diffusion models.
Bounded Differences#
The concept of “Bounded Differences” in a research paper likely refers to a technique or property related to limiting the magnitude of changes between successive states or values within a system. This is crucial in scenarios where uncontrolled fluctuations can negatively impact stability, accuracy, or efficiency. In the context of machine learning models, for instance, bounded differences might ensure that small changes in the input data do not lead to disproportionately large variations in the model’s output. This could improve model robustness and make it more predictable. Bounding the differences between iterations might be important in optimization algorithms for preventing oscillations or divergence. In other domains, like differential privacy, bounded differences are used to guarantee a level of privacy protection by constraining the impact of individual data points on the overall result. The specific implementation and application of bounded differences will be highly dependent on the specific problem being addressed in the paper. A deeper look into the context of “Bounded Differences” in the paper is needed to fully understand its significance and how the authors leverage it to their advantage.
Skip Prediction Steps#
The concept of “Skip Prediction Steps” in diffusion models centers on accelerating the denoising process without compromising image quality. The core idea is to intelligently bypass certain noise prediction steps during the iterative denoising procedure, leveraging the inherent redundancy in the process. Strategies for identifying skippable steps are crucial and often rely on analyzing the latent representations at different timesteps. Methods may utilize low-order differences or higher-order derivatives to gauge the stability and predictability of the denoising process. A key challenge is striking a balance between sufficient acceleration and preserving output fidelity. Adaptive approaches that tailor the number of skipped steps to the input prompt or characteristics of the generated image are particularly promising. While effective, this approach requires careful error analysis to prevent accumulating errors over multiple skipped steps. Ultimately, “Skip Prediction Steps” presents a promising avenue for enhancing the efficiency of diffusion models for real-time and interactive applications.
Third-Order Criterion#
The “Third-Order Criterion” section likely details a novel method for determining optimal skipping steps within a diffusion model’s denoising process. Instead of a fixed approach, this method leverages the third-order differential distribution of latent variables to identify redundancy. This innovative approach suggests that the stability between temporally neighboring latent representations, indicated by the third-order difference, is crucial in determining whether noise prediction steps can be skipped. Higher-order differences reveal more subtle patterns of redundancy not apparent in first or second-order analyses. This dynamic strategy enables AdaptiveDiffusion to adaptively adjust the number of noise prediction steps for each prompt, resulting in significant speed improvements without sacrificing output quality. The criterion likely involves a threshold-based decision, where a high third-order difference signals a need for a full noise prediction step, whereas a low difference signifies redundancy and allows for a step to be skipped. The effectiveness of this approach is empirically validated through experiments demonstrating speedup and quality preservation across various models and tasks, showcasing its generalization capability.
Ablation Experiments#
Ablation studies systematically remove components of a model or process to assess their individual contributions. In the context of this research paper, ablation experiments would likely involve systematically removing or varying aspects of the AdaptiveDiffusion method to determine their impact on overall performance. This might include removing or altering the third-order estimator, modifying the step-skipping strategy parameters (e.g. threshold), or comparing different noise prediction models. The results of these experiments would help to quantify the relative importance of each component and verify that they contribute to the observed improvements in speed and quality. Careful selection of ablation settings is crucial; changes should be made in isolation or in a controlled manner, allowing for a clear understanding of each component’s impact. The ultimate goal is to provide strong evidence supporting the design choices made in AdaptiveDiffusion and demonstrate that it’s not a single component but rather the interaction of all components that achieve the reported improvements. A thorough analysis of the results would highlight which elements are most crucial, potentially revealing areas where further optimization efforts might be beneficial.
More visual insights#
More on figures

This figure illustrates the process of the proposed AdaptiveDiffusion method. It shows how a third-order estimator is used to determine if noise prediction steps can be skipped (reusing previous results) or if new calculations are needed. This adaptive approach improves efficiency while maintaining the quality of the final denoised output. The figure highlights the key components: noise prediction model, scheduler, latent cache, third-order estimator, and noise cache.

This figure compares four different denoising strategies in diffusion models. (a) shows the standard full-step approach. (b), (c), and (d) demonstrate different acceleration methods: (b) AdaptiveDiffusion skips some noise prediction steps but maintains full latent updates; (c) shows a simple halving of both noise prediction and latent update steps in SDXL; and (d) shows a halving of noise prediction steps but full latent update steps in SDXL. The figure visually compares the output image quality for each method.

This figure examines the relationship between different order differential distributions (noise and latent) and the optimal skipping path determined through a greedy search algorithm for a single prompt during the denoising process. It demonstrates that while lower-order differences show weak or no correlation with optimal skipping, the relative 3rd-order latent difference provides a much clearer signal indicating which steps can be skipped during denoising.

This figure demonstrates the effectiveness of the proposed third-order estimator for predicting the optimal skipping path in AdaptiveDiffusion. Subfigure (a) visually compares the third-order estimated path with the optimal path found through a greedy search, showing a close agreement in their distribution. Subfigure (b) shows the latent error between using the full-step method and using the estimated skipping path, demonstrating that the error remains relatively low throughout the denoising process. Finally, subfigure (c) presents a statistical analysis using χ² tests and p-values to show the high correlation between the estimated and optimal skipping paths for a moderate number of skipping steps, validating the estimator’s ability to accurately predict skipping decisions.

This figure compares the denoising paths for two different prompts using the Stable Diffusion XL model. Each path represents the steps taken during the image generation process, with each step involving a noise prediction. The figure demonstrates that different prompts may require a different number of steps to reach a similar final image quality. Prompt 1 required fewer steps than Prompt 2. The figure also shows the LPIPS and PSNR scores for each path to indicate the similarity between the generated images and the original image.

This figure compares denoising paths for two different prompts using SDXL. It shows that different prompts require a different number of denoising steps to produce high-quality images. This illustrates the need for an adaptive approach, as some prompts may require fewer steps than others to achieve similar results.

This figure visualizes the skipping paths determined by two different methods (greedy search and the proposed third-order estimator) and shows the distribution of the number of skipped noise update steps. The greedy search method aims to find the optimal skipping path, while the third-order estimator provides a more efficient way to predict skipping steps. The distribution shows how frequently different numbers of steps were skipped during image generation.

This figure demonstrates that different prompts may require different numbers of denoising steps to produce high-quality images. It shows two examples with different prompts, illustrating how many steps were skipped while still maintaining high image quality.

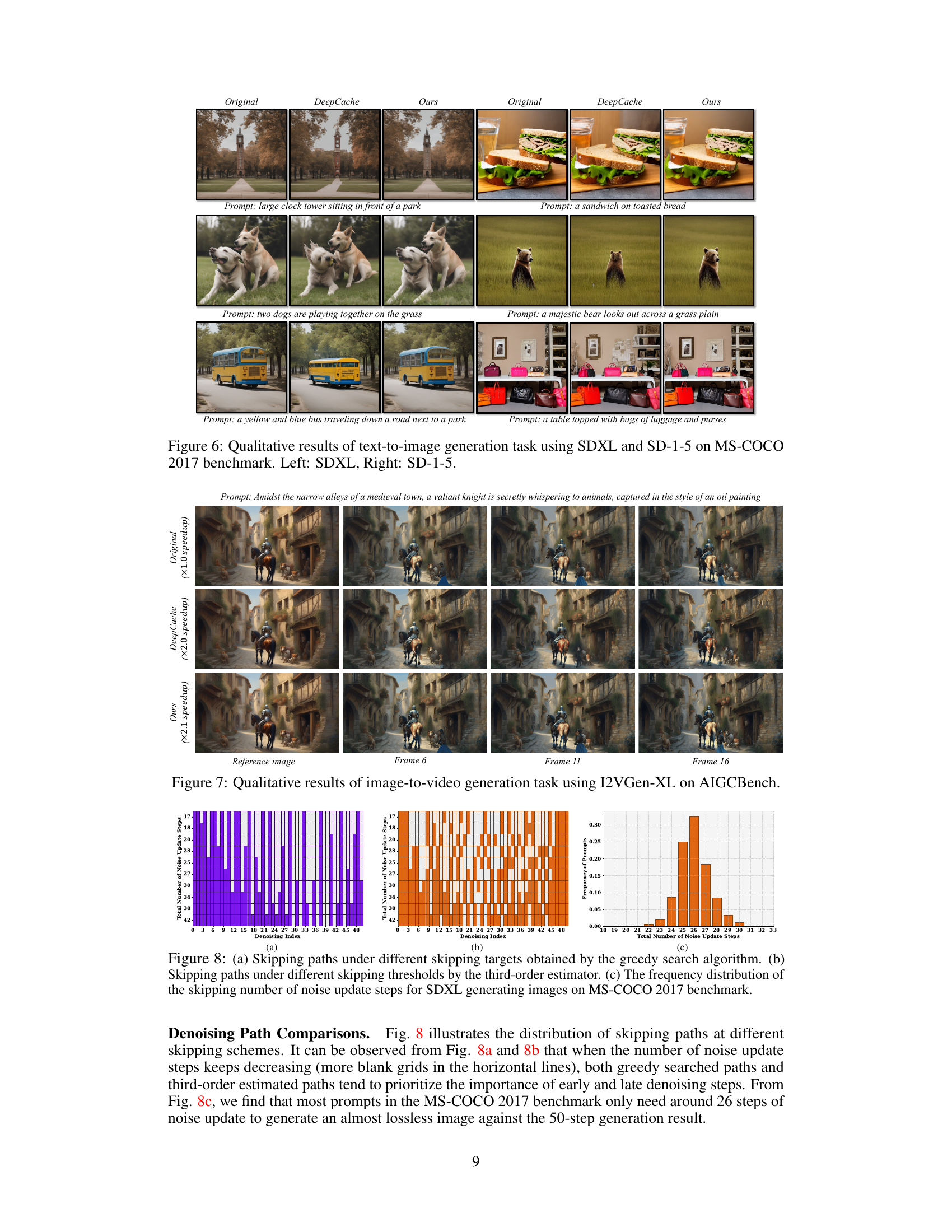
This figure shows a qualitative comparison of image-to-video generation results using three different methods: the original method, DeepCache, and the proposed AdaptiveDiffusion method. Each method’s output is shown for different frames (6, 11, and 16) of a generated video. The goal is to demonstrate the quality and speed improvements achieved by AdaptiveDiffusion, showcasing comparable visual quality to the original method but with significantly faster generation speeds compared to DeepCache. The prompt used for video generation is: ‘Amidst the narrow alleys of a medieval town, a valiant knight is secretly whispering to animals, captured in the style of an oil painting.’
More on tables

This table presents a quantitative comparison of the proposed AdaptiveDiffusion method against the DeepCache baseline on the ImageNet 256x256 dataset for conditional image generation. Metrics include PSNR (Peak Signal-to-Noise Ratio), LPIPS (Learned Perceptual Image Patch Similarity), and FID (Fréchet Inception Distance). Memory usage (Mem), multiply-accumulate operations (MACs), latency, and speedup ratio are also reported, providing a comprehensive evaluation of both the quality and efficiency gains achieved by the proposed method.

This table presents a quantitative comparison of the proposed AdaptiveDiffusion method against the Deepcache baseline on video generation tasks. The metrics used for evaluation include PSNR (Peak Signal-to-Noise Ratio), LPIPS (Learned Perceptual Image Patch Similarity), and FVD (Fréchet Video Distance), reflecting both the quality of individual frames and the temporal coherence of the generated videos. The table also shows memory usage (Mem), MACs (Multiply-Accumulate operations, a measure of computational cost), latency, and the speedup factor achieved by each method compared to the original, full-step video generation process. Two different video generation models are evaluated: I2VGen-XL and ModelScopeT2V.
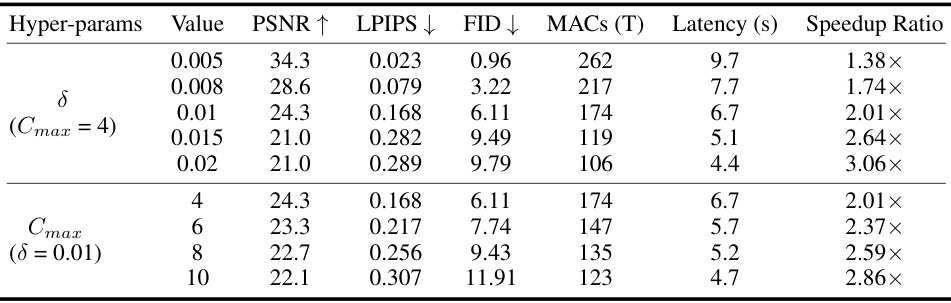
This table presents the ablation study results on the hyperparameters (δ and Cmax) of the proposed AdaptiveDiffusion method. It shows the impact of varying the skipping threshold (δ) and the maximum number of continuous skipping steps (Cmax) on the performance metrics (PSNR, LPIPS, FID, MACs, Latency, and Speedup Ratio) when using the 50-step Euler sampling scheduler for SDXL on the MS-COCO 2017 dataset. The results demonstrate the trade-off between speed and image quality when adjusting these hyperparameters.

This table shows the ablation study on different sampling steps (50, 25, 15, and 10). For each step count, it provides the PSNR, LPIPS, and FID scores, along with the total number of Multiply-Accumulate operations (MACs), latency in seconds, and speedup ratio compared to the full 50-step method. This demonstrates the effectiveness of AdaptiveDiffusion in accelerating the denoising process even with a significantly reduced number of steps.
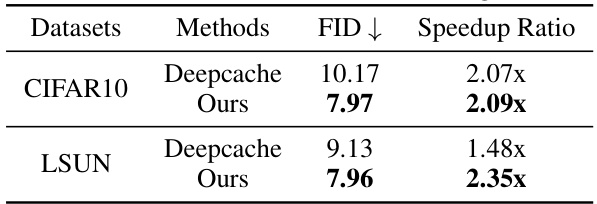
This table compares the performance of Deepcache and the proposed AdaptiveDiffusion method on unconditional image generation tasks using two datasets: CIFAR10 and LSUN. The metrics reported are FID (Fréchet Inception Distance), a measure of image quality, and speedup ratio, indicating the acceleration achieved by each method compared to a baseline. Lower FID values indicate better image quality, and higher speedup ratios signify faster generation times. The results show that AdaptiveDiffusion achieves both better image quality (lower FID) and faster generation speeds (higher speedup ratio) than Deepcache on both datasets.

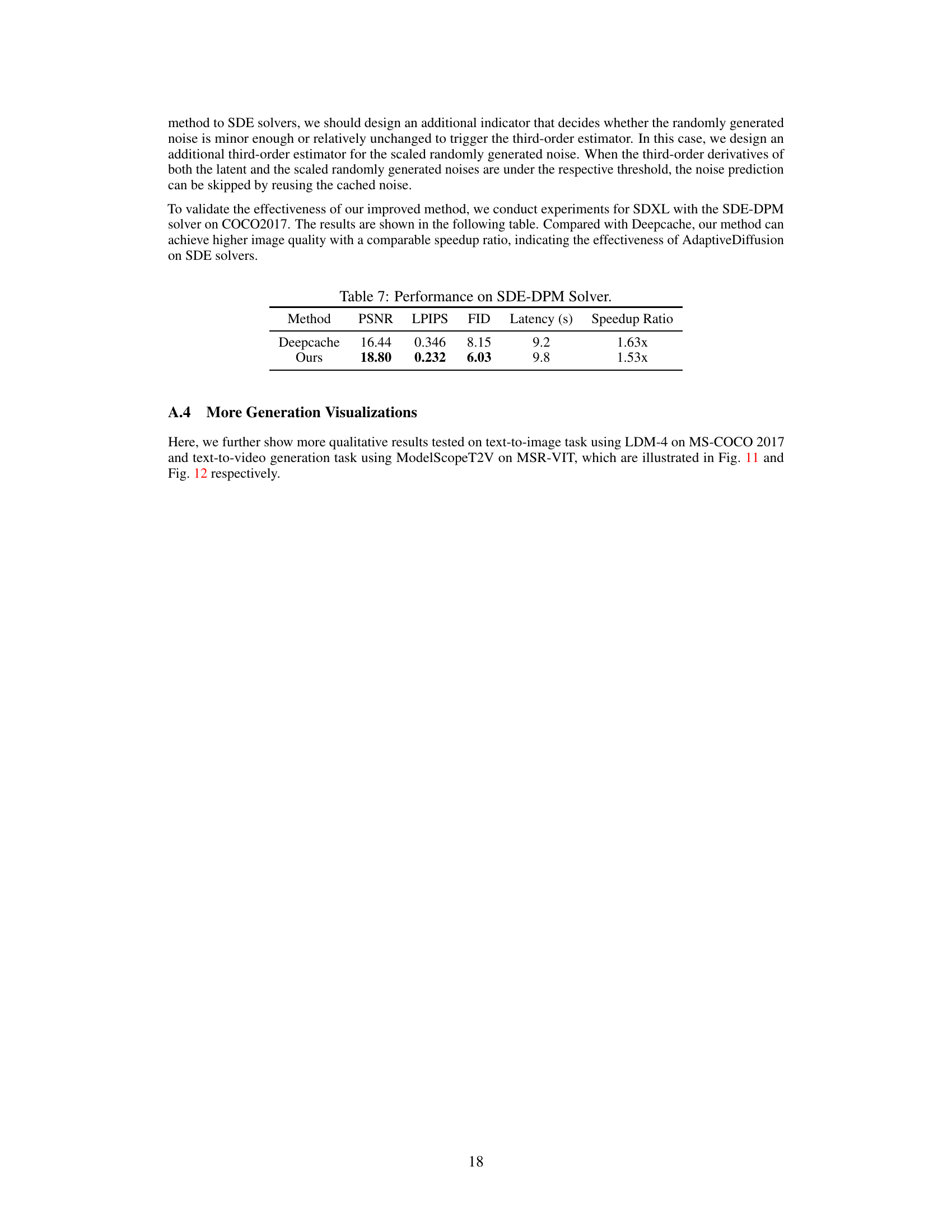
This table presents the performance comparison between DeepCache and the proposed AdaptiveDiffusion method using the SDE-DPM solver on the COCO2017 dataset. It shows that AdaptiveDiffusion achieves higher PSNR and lower LPIPS and FID scores compared to DeepCache, indicating better image quality. While AdaptiveDiffusion has a slightly higher latency, the speedup ratio remains comparable to DeepCache.
Full paper#