↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Distributional regression, aiming to estimate the conditional distribution of a target variable given covariates, is crucial for accurate forecasting, especially when precise uncertainty quantification is needed. Current methodologies often lack theoretical guarantees, making it difficult to assess the reliability and accuracy of the resulting forecasts. This paper addresses this gap by focusing on the Continuous Ranked Probability Score (CRPS) as a risk measure.
The paper establishes concentration bounds for estimation errors in model fitting, using CRPS-based empirical risk minimization. Furthermore, it provides theoretical guarantees for model selection and convex aggregation, improving forecast accuracy and reliability. The results are validated through applications to diverse models and datasets (QSAR aquatic toxicity and Airfoil self-noise), showcasing their practical significance and broad applicability.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in distributional regression and related fields. It provides rigorous theoretical guarantees for model fitting, selection, and aggregation using the CRPS, addressing a significant gap in the current literature. The results are applicable to a wide range of models, and the weaker moment assumptions extend applicability beyond previous work. This opens up new avenues for research in developing more accurate and reliable forecasting methods with improved uncertainty quantification.
Visual Insights#
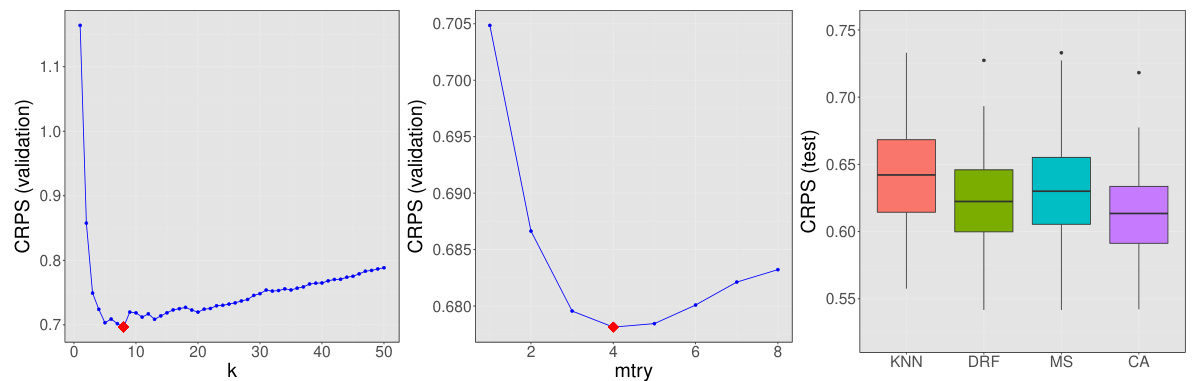
This figure displays the results of hyperparameter tuning and model comparison for the QSAR dataset. The left and center panels show the validation error (CRPS) curves for the KNN (k neighbors) and DRF (mtry variables) models, respectively, as the hyperparameters are varied. The minimum validation errors indicate the optimal hyperparameter settings (k=8, mtry=4). The right panel presents boxplots of the test error (CRPS) obtained for KNN, DRF, model selection (selecting the best of KNN and DRF based on validation error), and convex aggregation (combining KNN and DRF predictions) over 100 repetitions. This visualization demonstrates the impact of hyperparameter tuning and model aggregation on predictive accuracy.
Full paper#