Online Weighted Paging with Unknown Weights

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it tackles a critical limitation in online weighted paging, a fundamental problem in online algorithms. By addressing the issue of unknown page weights, this research opens up new avenues for algorithm design in various applications, including multi-level caching and resource management. Its results directly impact the design and performance of online systems, prompting further work in similar areas. The approach used, which combines online algorithms with bandit-like feedback, could inspire more efficient algorithms for cost-sampling in other applications.

Visual Insights

#

This figure visualizes a single step in the interaction between the fractional and integral algorithms. It shows how the integral algorithm maintains an instance of the fractional algorithm (ONF), along with a probability distribution over valid cache states. Upon a page request, the fractional algorithm updates its solution, and the integral algorithm adjusts its probability distribution to remain consistent and balanced (also illustrated is the process of handling samples).

In-depth insights

#

Unknown Weights OWP

#

The study of “Unknown Weights OWP” delves into the challenges of online weighted paging where the cost of fetching each page is initially unknown. This departs from traditional OWP which assumes prior knowledge of page weights. The core problem lies in balancing exploration (learning page weights through sampling) and exploitation (optimizing cache usage based on current weight estimates). The paper likely proposes a novel algorithm that addresses this exploration-exploitation tradeoff. A key technical aspect will be how the algorithm uses weight samples to estimate fetching costs dynamically and efficiently, potentially employing techniques like confidence bounds (UCB/LCB) commonly found in multi-armed bandit problems. The results would likely demonstrate a competitive ratio (performance relative to optimal offline strategy), possibly including a regret term quantifying the penalty for initially not knowing the weights. Such an algorithm could have significant implications for various real-world systems involving caching and resource management where costs are initially uncertain but learnable through observation.

Fractional & Rounding

#

The core of many randomized online algorithms lies in a two-stage approach: solving a fractional relaxation of the problem, followed by a randomized rounding scheme to obtain an integral solution. This paper cleverly addresses the challenge of unknown weights in the online weighted paging problem by integrating these two steps. The fractional algorithm employs optimistic confidence bounds to learn page weights from samples gathered during the process, fostering efficient exploration. The rounding scheme, in contrast, uses pessimistic confidence bounds, ensuring a safe and deterministic update of the probability distribution over integral states. This design cleverly addresses the dependency between sampling (done in rounding) and the algorithm’s competitiveness (reliant on fractional solutions). A key innovation is the careful interface between these two stages, managing sample acquisition and utilization to simultaneously guarantee a near-optimal competitive ratio and a sublinear regret. This combined approach represents a significant contribution, effectively extending the success of traditional fractional/rounding techniques to a significantly more challenging problem landscape.

Optimistic Bandit

#

The concept of an “Optimistic Bandit” algorithm stems from the multi-armed bandit problem, where an agent sequentially chooses from several options (arms) with unknown reward distributions. Optimistic strategies assume initially that all arms have high rewards, exploring them to refine estimates. As evidence accumulates, the algorithm updates its beliefs, becoming increasingly less optimistic but still prioritizing options that seem promising. This approach balances exploration and exploitation effectively. Upper Confidence Bound (UCB) algorithms exemplify this, calculating confidence intervals for each arm’s expected reward and choosing the arm with the highest upper confidence bound. The optimism in UCB guides the exploration by selecting arms with potentially high rewards even with limited evidence, a key difference from other bandit algorithms which might focus solely on exploiting the currently best performing arms. The success of optimistic bandit algorithms relies on the principle that early exploration is valuable, potentially revealing better arms otherwise missed. However, over-optimism can lead to suboptimal performance if it prolongs the exploration phase excessively. Therefore, careful design of confidence bounds is crucial to balance exploration with exploitation for optimal performance.

Regret Bound

#

The concept of a ‘Regret Bound’ in online learning algorithms, particularly within the context of online weighted paging with unknown weights, is crucial. It quantifies the suboptimality of an algorithm that learns the page weights over time compared to an optimal algorithm that knows the weights beforehand. A tight regret bound is desirable, indicating that the algorithm’s performance approaches the optimal solution efficiently. In this specific problem, the regret bound likely incorporates two elements: competitive ratio and additional regret. The competitive ratio reflects how the algorithm’s total cost compares to the optimal cost in the worst-case scenario, given the unknown weights. The additional regret term captures the cost incurred due to the learning process itself; this cost should decrease over time as the algorithm gathers more information about the page weights. A good regret bound will therefore demonstrate a small competitive ratio and a sublinear additive regret term. The latter could be a function of the number of requests processed, suggesting that the learning process is efficient. Analyzing and understanding this bound provides critical insight into the algorithm’s efficiency and its convergence properties.

Future Learning

#

A section on “Future Learning” in this context would explore avenues for extending the research on online weighted paging with unknown weights. Algorithmic improvements could focus on refining the interface between the fractional solution and rounding scheme, potentially exploring alternative rounding techniques or adaptive sampling strategies. Theoretical advancements might involve investigating the impact of different weight distributions or exploring alternative competitive ratio bounds under various assumptions. Practical applications should be considered, such as applying the model to more complex caching scenarios like those encountered in distributed systems or hierarchical memory structures. Further research into the trade-offs between exploration and exploitation in the context of bandit feedback is crucial. Finally, a thoughtful discussion of the limitations of this model and directions for future work addressing those limitations would complete the section.

More visual insights

#

More on figures

This figure visualizes a single step in the interaction between the fractional and integral algorithms. It shows how the fractional algorithm maintains a probability distribution over cache states and uses this to guide the integral algorithm’s decision-making. The integral algorithm maintains consistency with the fractional algorithm’s solution and ensures that the probability distribution maintains balance. When the fractional algorithm demands a sample, the integral algorithm provides one. The figure also showcases how the algorithm handles requests (by fetching the requested page if necessary, adjusting the fractional solution, and updating the probability distribution), and demonstrates the communication between the fractional and integral components, especially the exchange of samples and updates to the confidence bounds.

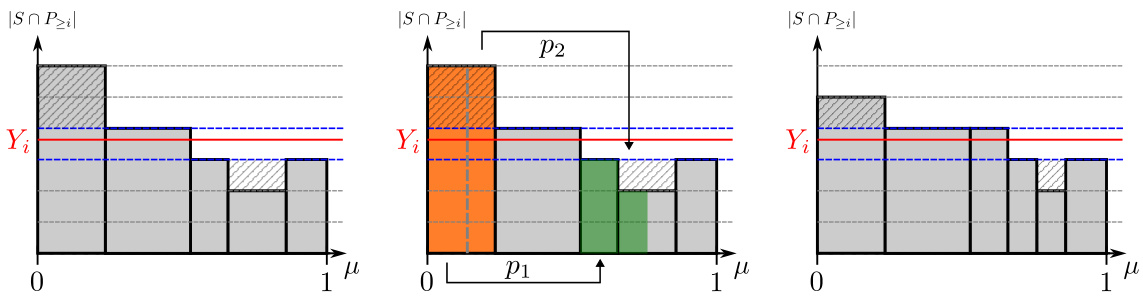
This figure visualizes a single step in the REBALANCESUBSETS procedure. Subfigure (a) shows the distribution of anti-cache states prior to this step; specifically, the x-axis is the probability measure, and the y-axis is the number of pages of class i and above in the anti-cache, i.e., m := |S∩P>i|. The red line is Yi, which through consistency, is the expectation of m; the blue dotted lines are thus the allowed values for m, which are [Yi], [Yi]]. The total striped area in the figure is the imbalance measure, formally defined in Definition B.2. Subfigure (b) shows a single rebalancing step; we choose the imbalanced anti-cache S that maximizes |m - Yi|; in our case, m > Yi, and thus we match its measure with an identical measure of anti-cache states that are below the upper blue line, i.e., can receive a page without increasing imbalance. Then, a page of class i is handed from S to every matched state S’; note that every matched state might get a different page from S, but some such page in S \ S’ is proven to exist. Finally, Subfigure (c) shows the state after the page transfer; note the decrease in imbalance that results. The REBALANCESUBSETS procedure performs such steps until there is no imbalance; then, the procedure would advance to class i - 1.

This figure visualizes a single step in the process of handling a page request. The fractional algorithm maintains a fractional solution, and the integral algorithm maintains a probability distribution over valid integral cache states. The fractional algorithm provides samples to the integral algorithm whenever the total fraction of a page evicted reaches an integer. The integral algorithm provides samples to the fractional algorithm whenever it requires one.

Full paper

#