↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Deep learning models exhibit emergence—a sudden ability to solve new problems as resources increase—and predictable scaling laws. Understanding the relationship between these two phenomena is crucial. Existing models either focus on emergence or scaling laws, lacking a unified framework.
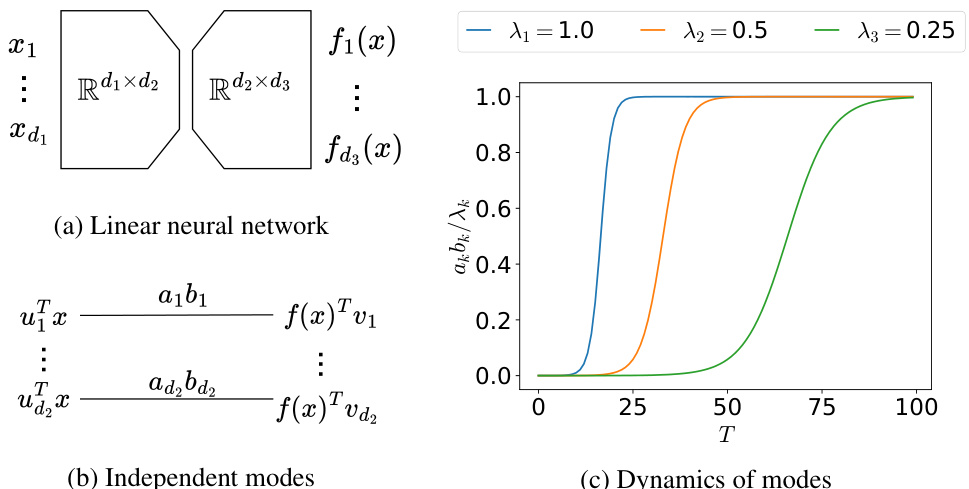
This paper introduces a novel, analytically tractable multilinear model to address this gap. By representing skills as orthogonal basis functions and using a multilinear model with a layered structure mimicking neural networks, they derive analytical expressions for skill emergence and scaling laws with respect to training time, data size, model size and computational resources. This model accurately predicts the stage-like emergence of multiple skills observed in experiments, highlighting the role of layered structure and power-law skill distribution in this phenomenon.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers studying deep learning scaling laws and emergence. It offers an analytically tractable model that explains skill emergence in deep learning models, bridging the gap between continuous scaling laws and the discontinuous emergence of new skills. This model provides testable predictions, opening avenues for further research into deep learning mechanisms and improving model training strategies.
Visual Insights#
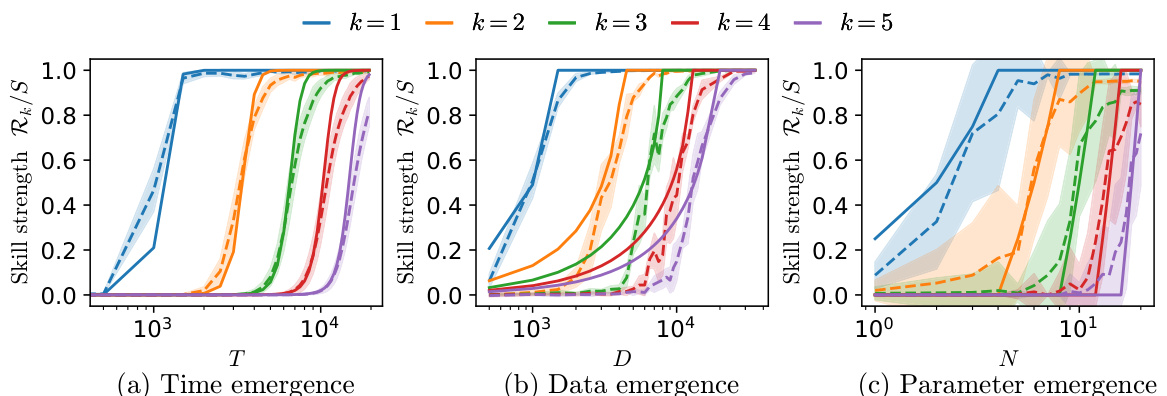
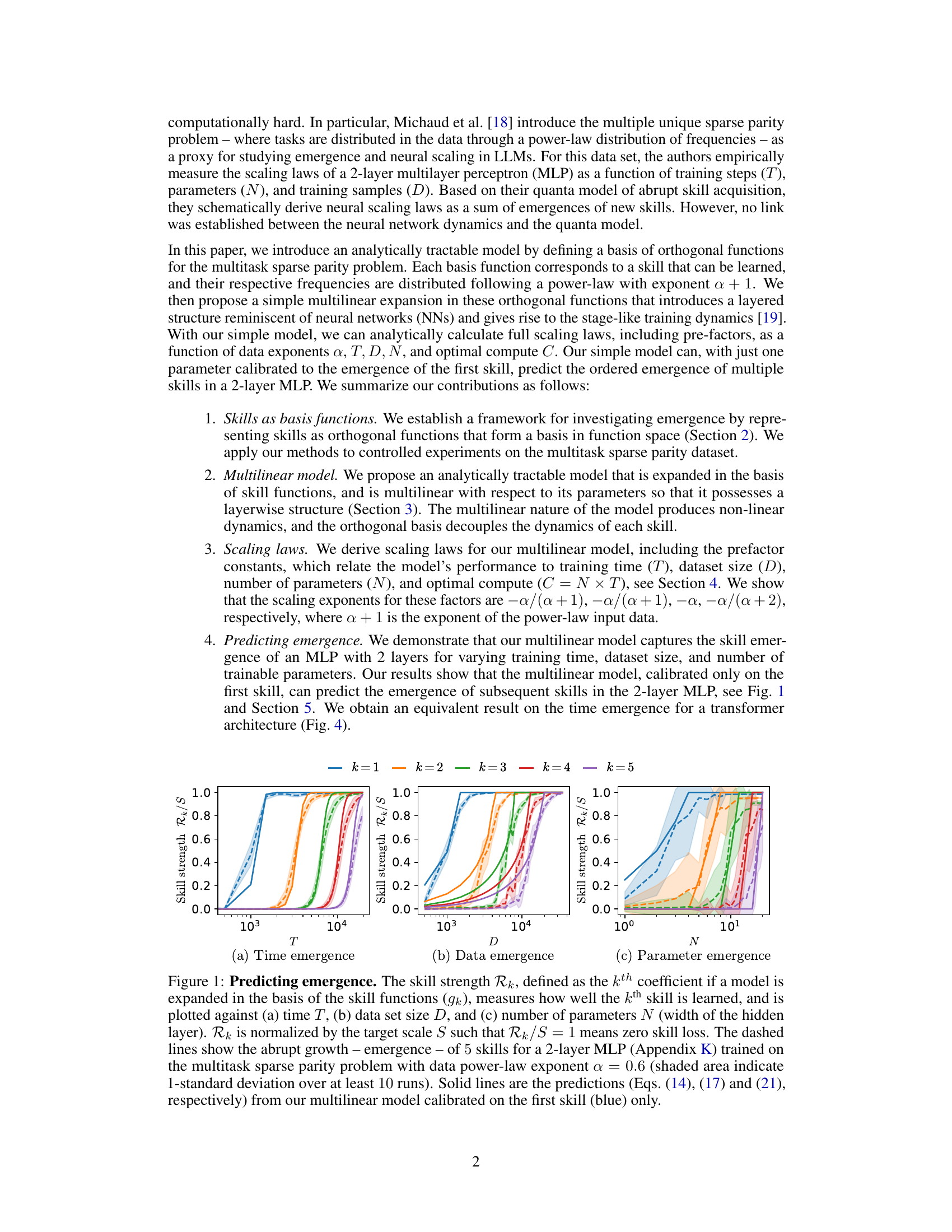
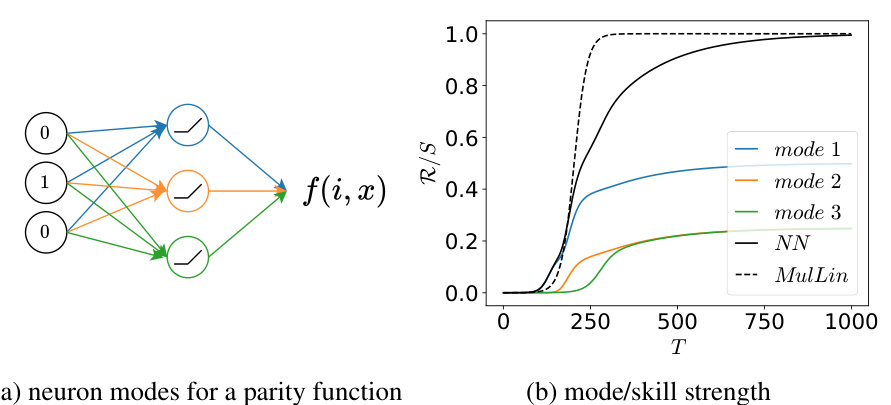
This figure shows the emergence of five skills in a two-layer multi-layer perceptron (MLP) neural network trained on a multitask sparse parity problem. The x-axis of each subplot represents a different training parameter: time (T), dataset size (D), and number of parameters (N). The y-axis represents the skill strength (Rk/S), which is a normalized measure of how well a particular skill has been learned. Dashed lines show the empirically observed skill emergence in the MLP; solid lines show the predictions of an analytically solvable multilinear model. The model, calibrated using only the emergence of the first skill, accurately predicts the emergence of the remaining skills.

This table shows the dataset used for the multitask sparse parity problem. It displays the control bits (one-hot encoding of the task), skill bits (binary string with m=3 relevant bits), the target value (y), a vector representation (M) of the relevant bits used to compute the parity, and the values of the skill basis functions (gk) for each example. The frequencies of the different parity tasks follow an inverse power law distribution, a key element of the multitask problem. The skill basis functions are orthogonal and form a basis set to represent skills.
In-depth insights#
Skill Emergence#
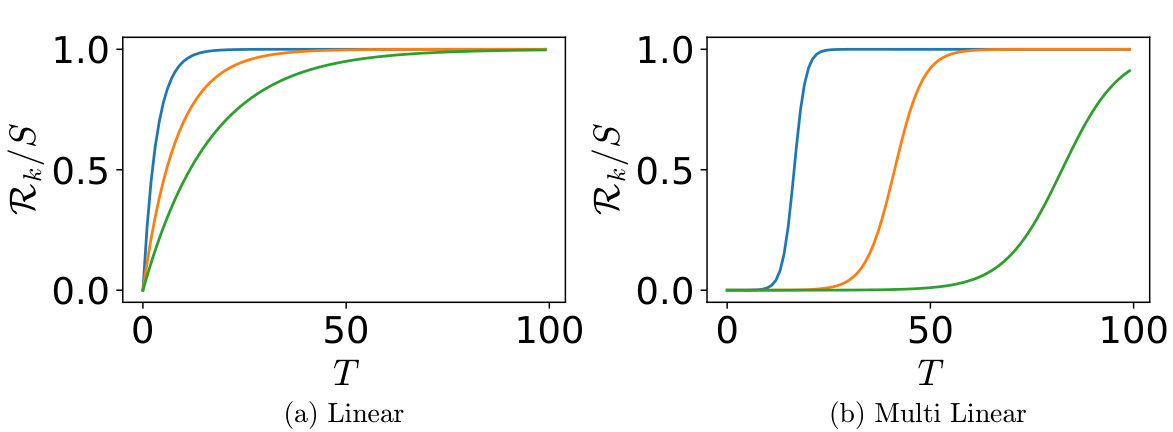
The concept of skill emergence, central to the paper, explores how deep learning models seemingly acquire new abilities (skills) abruptly as training progresses. The authors frame skills as orthogonal basis functions within a multi-linear model, allowing for analytical solutions. This approach reveals analytic expressions for skill emergence, shedding light on the relationship between training time, data size, model size, and computational resources. Power-law scaling laws are derived, aligning with empirical observations in neural network scaling. The model predicts the sigmoidal emergence of skills—capturing a gradual increase leading to a sudden, near-complete skill acquisition. Simulations on multitask sparse parity datasets confirm these predictions, providing strong evidence for the framework’s accuracy. Importantly, the analysis decouples skill acquisition dynamics, simplifying the complex interactions within deep neural networks.
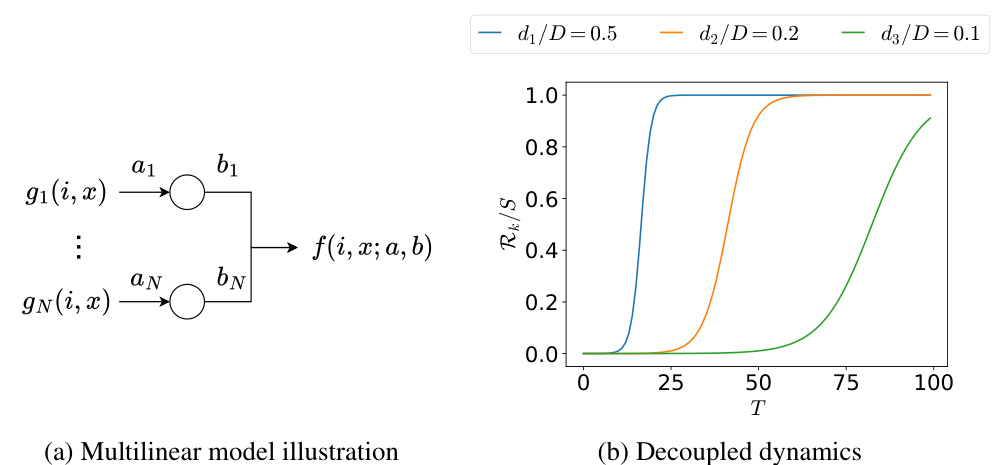
Multilinear Model#
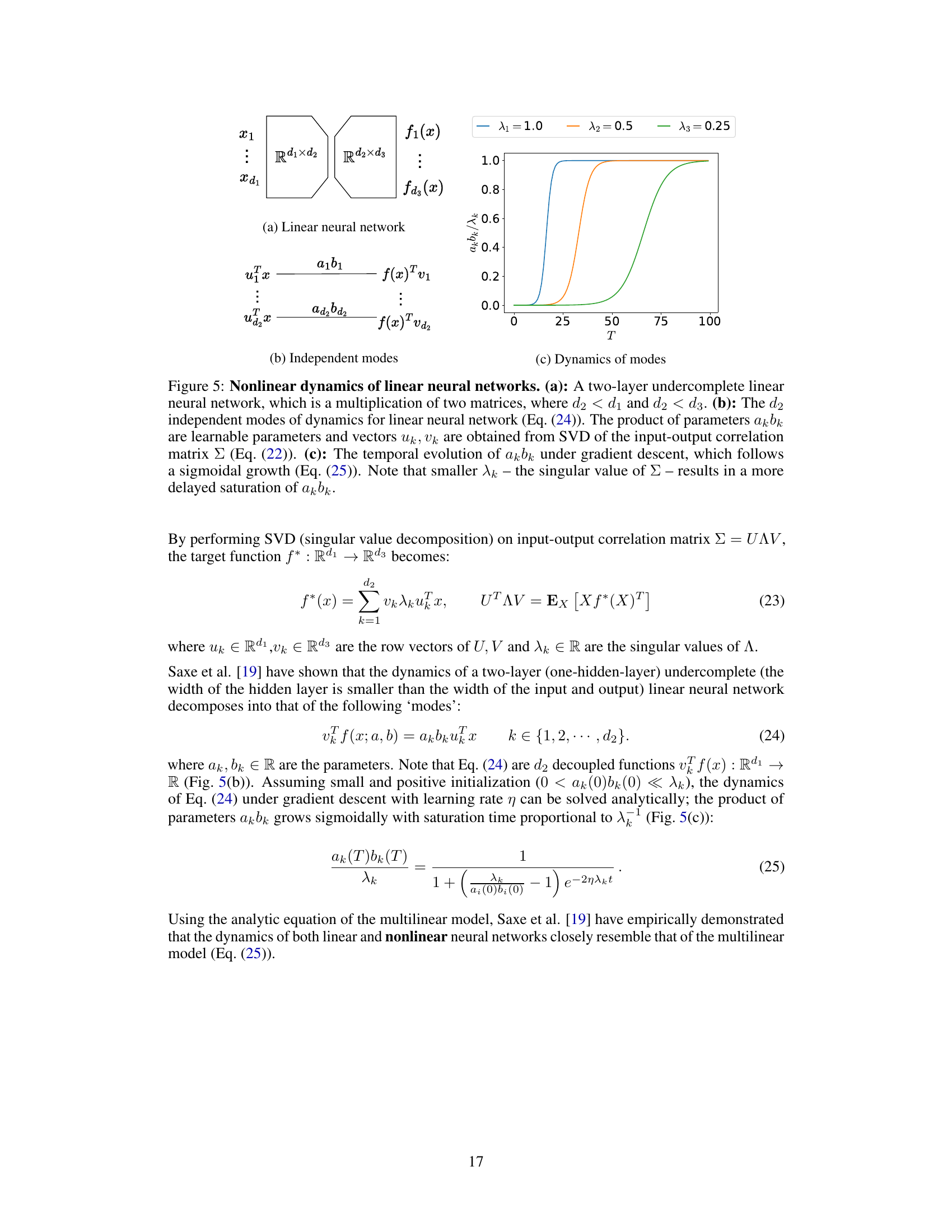
The core of the research paper revolves around a novel multilinear model designed to demystify emergence and scaling laws in deep learning. This model cleverly sidesteps the complexities of neural networks by representing skills as orthogonal basis functions. The multilinear structure of the model, a product of its parameters, directly mirrors the layered architecture of neural networks, providing a simplified, yet insightful, lens for studying skill acquisition. The model’s analytical tractability is a significant advantage, enabling the derivation of precise scaling laws for factors like training time, data size, and model parameters. This allows for quantifiable predictions about when and how new skills emerge, offering a powerful framework for understanding the underlying mechanisms that drive emergence in deep learning. The model’s predictive power is further demonstrated through its capacity to accurately capture experimental results observed in multilayer perceptrons (MLPs) and even transformers, highlighting the general applicability of its fundamental principles to various network architectures.
Scaling Laws#
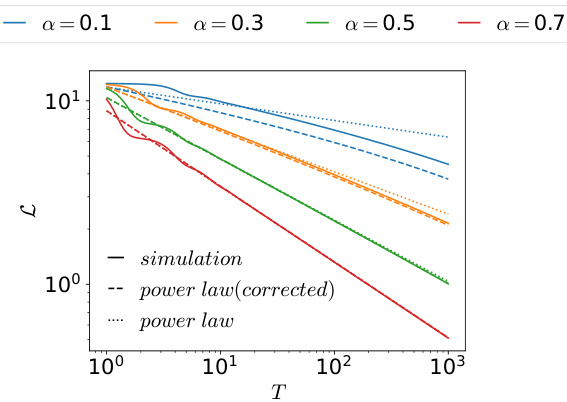
The study of scaling laws in deep learning is crucial for understanding how model performance changes with increased resources. This paper delves into these scaling laws, examining the relationship between loss and training time, data size, model size, and optimal compute. The authors present a novel multilinear model that captures the sigmoidal skill emergence observed in neural networks. The model’s simplicity is a major advantage, allowing for analytical derivations of scaling laws, including prefactor constants. These derivations reveal power-law relationships with exponents that match empirical observations from prior work. The orthogonal basis of skill functions used by this model greatly simplifies the analysis, leading to a deeper understanding of how different factors contribute to model performance and skill acquisition. The model’s predictions align well with experimental results obtained from neural networks, especially in capturing the ordered emergence of multiple new skills. This makes the model an excellent tool for understanding and predicting emergence phenomena in deep learning.
NN Emergence#
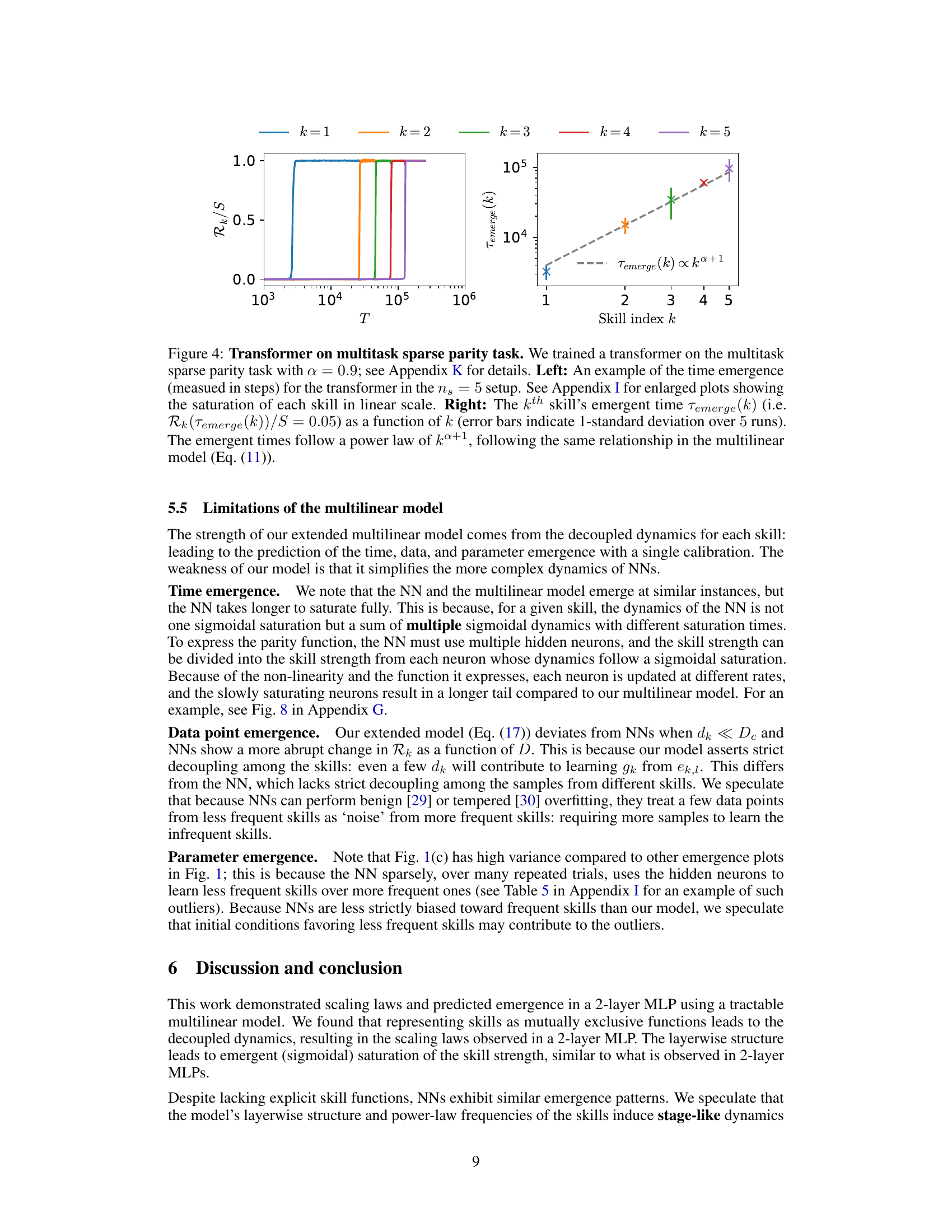
The paper investigates the phenomenon of NN emergence, where neural networks seemingly acquire new abilities abruptly as training progresses. The authors propose a multilinear model, demonstrating analytically how multiple skills emerge in a stage-like manner as training time, data size, or model size increase. This model utilizes orthogonal functions representing individual skills, offering an analytically tractable framework for studying emergence and scaling laws. Notably, the multilinear model accurately predicts the ordered emergence of skills in both multilayer perceptrons and transformer architectures. This prediction capability showcases the model’s explanatory power, suggesting that the interaction between layers, coupled with a power-law distribution of skill frequencies in the data, underlies the observed stage-like emergence. While the multilinear model simplifies the complexity of actual neural network dynamics, it provides a valuable theoretical lens, highlighting the potential of analytically tractable models to capture key emergent phenomena in deep learning.
Model Limits#
The limitations of the proposed model stem primarily from its simplified assumptions about neural network dynamics. The decoupled nature of skill acquisition, while analytically convenient, fails to capture the complex interactions and dependencies observed in real-world neural networks. The model’s reliance on orthogonal skill functions, although simplifying the analysis, restricts its applicability to datasets with clearly separable skills; in practice, skills frequently overlap and interact. Furthermore, the model’s simplified assumptions of power-law distributions of skill frequencies and dataset size are idealizations which may not accurately reflect empirical data. The stage-like training assumption, while illuminating, might not always hold in real-world scenarios, where the emergence of multiple skills can be more gradual and less clearly defined. While the multilinear model offers valuable insights into the scaling laws and skill emergence, the model’s limitations highlight the need for more sophisticated theoretical frameworks to fully capture the rich, complex dynamics of neural network learning. Future research should focus on developing models that address the non-linear interactions between skills and the impact of non-idealized data characteristics.
More visual insights#
More on figures
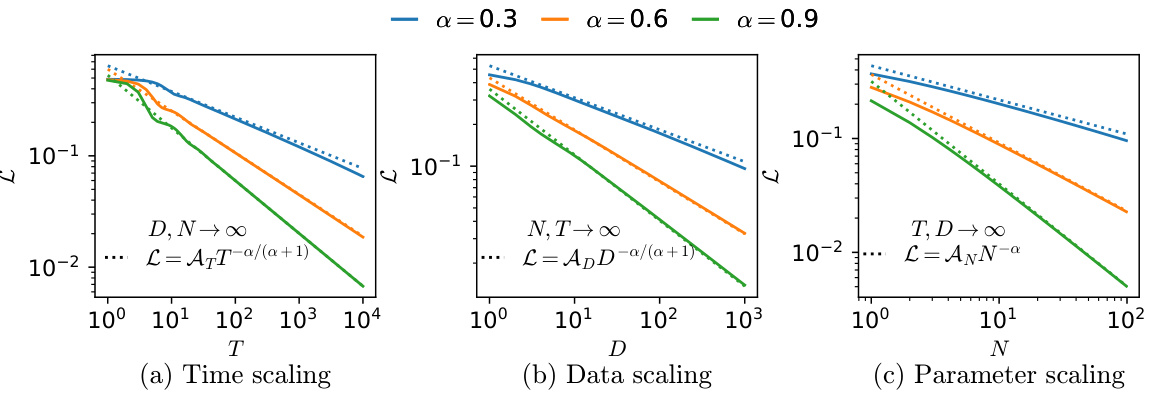
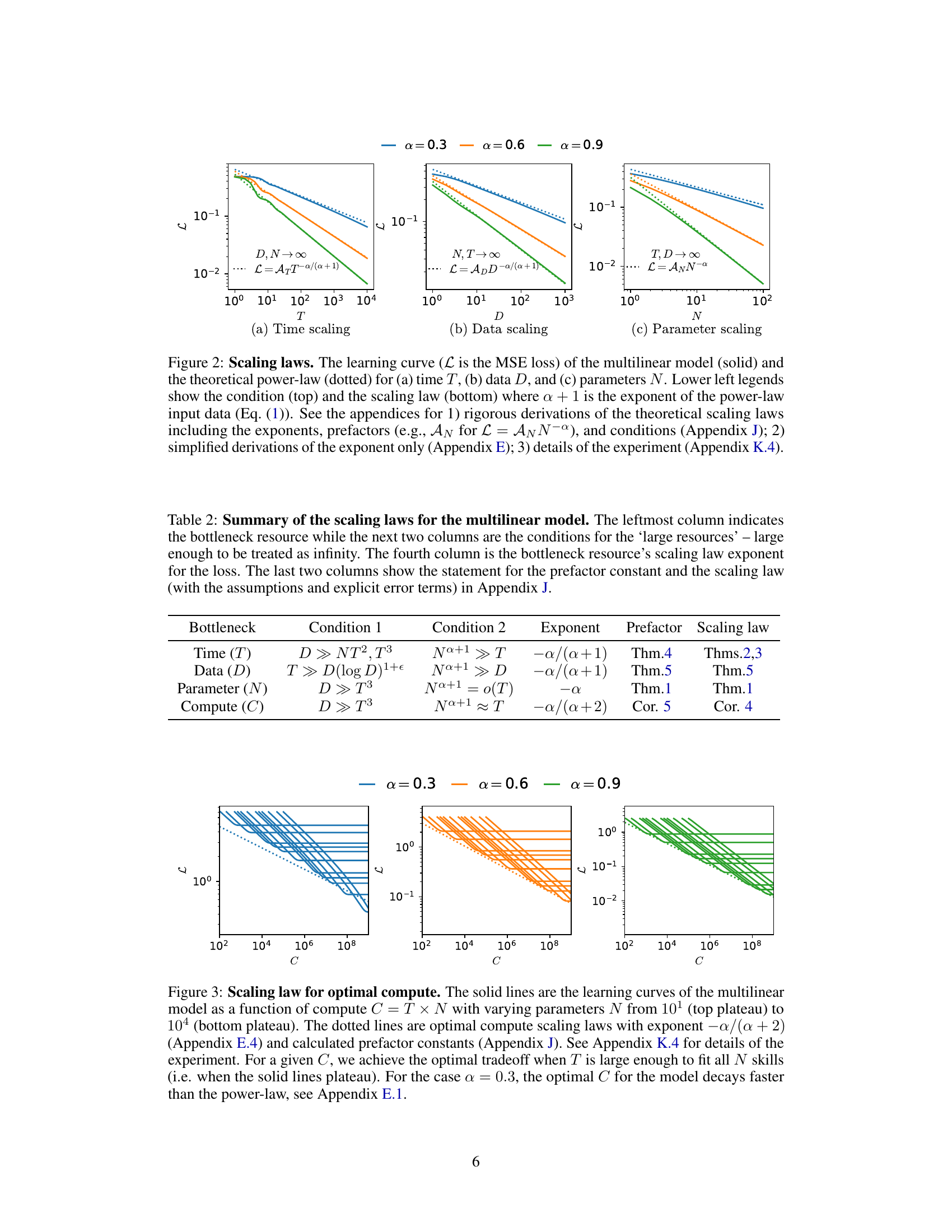
This figure compares simulation results of the multilinear model with the theoretical scaling laws for training time, dataset size, and the number of parameters. The plots show that the multilinear model captures the power-law scaling behavior observed empirically in deep neural networks, but with added prefactor constants. The appendices provide full mathematical derivations and details of the experimental setup.
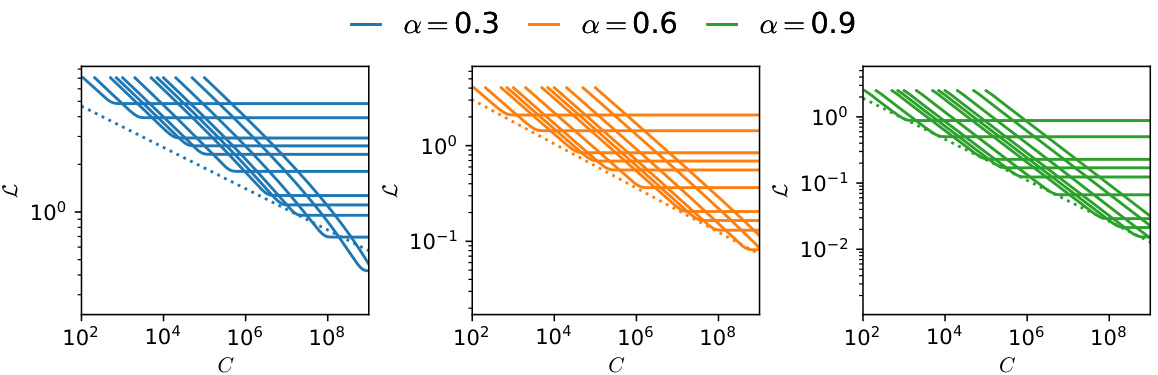
This figure shows the scaling law for optimal compute in the multilinear model. It plots the learning curves (loss vs compute) for different numbers of parameters (N) and compares them against the predicted optimal compute scaling laws. The optimal tradeoff is achieved when enough time (T) is used to fit all skills (parameters). For α = 0.3, the optimal compute decreases faster than the power law.
This figure shows the emergence of five skills in a two-layer multilayer perceptron (MLP) trained on the multitask sparse parity problem. The skill strength (Rk) is plotted against training time (T), dataset size (D), and number of parameters (N). The dashed lines represent the empirically observed skill emergence, showing a step-like increase in skill strength as the resources increase. The solid lines are predictions from an analytically tractable multilinear model, which accurately captures the emergence of skills using only a single fit parameter calibrated to the emergence of the first skill.
This figure shows the emergence of 5 skills in a 2-layer MLP trained on the multitask sparse parity problem, as measured by the skill strength Rk. The dashed lines represent empirical results showing an abrupt increase in skill strength with respect to training time (T), dataset size (D), and number of parameters (N). The solid lines are predictions from a multilinear model calibrated using only the first skill, demonstrating the model’s ability to predict the emergence of subsequent skills.
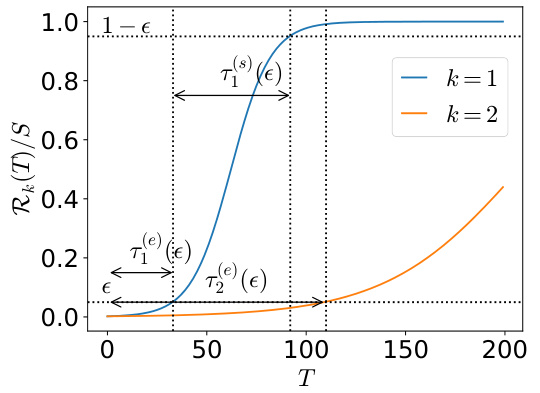
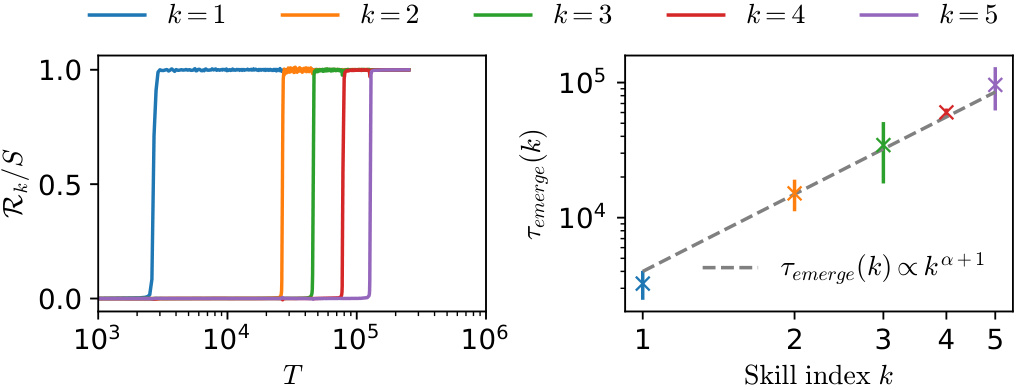
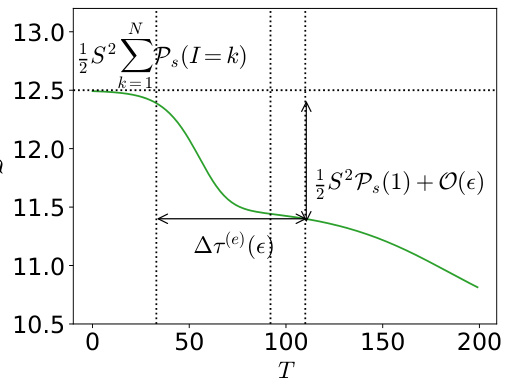
This figure illustrates the concept of stage-like training in the context of the multilinear model applied to the multitask sparse parity problem. Panel (a) shows the skill strength (Rk/S) as a function of time (T) for two skills (k=1 and k=2). The sigmoidal curves illustrate how each skill reaches near-saturation before the next skill begins to emerge. The emergent time (T(e)) and saturation time (T(s)) are graphically defined for each skill. Panel (b) shows the corresponding loss changes over time, highlighting the distinct stages of skill acquisition.
This figure shows the emergence of 5 skills in a 2-layer multilayer perceptron (MLP) trained on the multitask sparse parity problem. The skill strength, which represents how well a particular skill is learned, is plotted against training time (T), dataset size (D), and the number of parameters (N) in the model. The dashed lines show the empirical results, while the solid lines are the predictions of a simpler multilinear model. The shaded areas represent the 1-standard deviation over at least 10 runs of the experiment. The figure demonstrates that the multilinear model, even when only calibrated on the first skill, can accurately predict the emergence of subsequent skills as training time, data size, or model size increase. This suggests the multilinear model captures the essential dynamics of skill emergence in the MLP.
This figure shows the emergence of five skills in a two-layer Multilayer Perceptron (MLP) neural network trained on the multitask sparse parity problem. The skill strength (Rk) is plotted against training time (T), dataset size (D), and number of parameters (N). The dashed lines represent the empirical results showing an abrupt increase in skill strength (emergence), while the solid lines show predictions from a multilinear model. The multilinear model, calibrated using only the emergence of the first skill, accurately predicts the emergence of subsequent skills.
This figure compares the emergence of skills in a two-layer Multilayer Perceptron (MLP) neural network trained on a multitask sparse parity problem with the predictions of a simpler, analytically solvable multilinear model. The plots show the strength of five different skills (Rk/S) as a function of training time (T), dataset size (D), and the number of model parameters (N). The dashed lines represent the empirical results from the MLP, showing a step-like emergence of skills. The solid lines represent the predictions of the multilinear model, demonstrating that the model can accurately predict the emergence of multiple skills (after calibration to the first skill).
This figure shows the emergence of skills in a 2-layer MLP trained on the multitask sparse parity problem. The skill strength (Rk) is plotted against training time (T), dataset size (D), and the number of parameters (N). Dashed lines represent the empirically observed skill emergence, showing a sharp increase in skill strength. Solid lines are predictions from the authors’ analytically tractable multilinear model, which is only calibrated on the first skill’s emergence. The model successfully predicts the emergence of subsequent skills, demonstrating its ability to capture the key dynamics of skill acquisition in this problem.
This figure shows the emergence of skills in a 2-layer Multilayer Perceptron (MLP) neural network trained on the multitask sparse parity problem. The skill strength (Rk/S) is plotted against training time (T), dataset size (D), and number of parameters (N). The dashed lines represent the empirical results showing an abrupt increase in skill strength (emergence), while the solid lines are predictions from a simpler, analytically tractable multilinear model. This model, calibrated only on the first skill, accurately predicts the emergence of the other skills, demonstrating its effectiveness in capturing the essential dynamics of skill acquisition in the MLP.

This figure shows the emergence of five skills in a two-layer multi-layer perceptron (MLP) neural network trained on a multitask sparse parity problem. The skill strength (Rk) is plotted against training time (T), dataset size (D), and number of parameters (N). The dashed lines represent the observed skill emergence, while the solid lines show the predictions of a simpler multilinear model. The multilinear model, despite its simplicity, accurately predicts the emergence of multiple skills, demonstrating its effectiveness in capturing the key dynamics of skill acquisition in the MLP.

This figure shows the emergence of five skills in a two-layer multi-layer perceptron (MLP) trained on a multitask sparse parity problem. The skill strength (Rk) is plotted against training time (T), dataset size (D), and the number of parameters (N). The dashed lines represent the empirically observed skill emergence, while the solid lines show the predictions from a multilinear model. The figure demonstrates that the multilinear model, calibrated using only the emergence of the first skill, accurately predicts the emergence of subsequent skills as a function of T, D, and N. The shaded areas indicate the standard deviation over multiple runs of the experiment.
More on tables

This table summarizes the scaling laws derived for the multilinear model presented in the paper. It shows how the loss (MSE) scales with respect to time (T), data size (D), number of parameters (N), and optimal compute (C). Each row represents a different bottleneck resource (the most limited resource), and it specifies the conditions under which the scaling law holds (for the other resources being sufficiently large). The exponents and prefactors for the scaling laws are given, along with references to the theorems and corollaries in Appendix J where the rigorous derivations are presented.

This table presents the data for the multitask sparse parity problem used in the paper. It shows how the control bits (one-hot vectors) encode the specific parity tasks, with frequencies following an inverse power law. The skill bits are binary strings where colored bits are relevant, and the y-column is the target value calculated from those bits. The last columns provide the values of the skill basis functions.

This table summarizes the scaling laws derived for the multilinear model presented in the paper. It shows how the loss (L) scales with different resources (time (T), data size (D), number of parameters (N), and compute (C)). The table presents scaling exponents, and prefactor constants for these scaling laws. Note that the conditions listed describe the circumstances under which the scaling laws are valid, highlighting the need for sufficiently large resource values to treat them as infinite in the derivation.

This table summarizes the scaling laws derived for the multilinear model presented in the paper. It shows how the loss (L) scales with respect to time (T), data size (D), number of parameters (N), and compute (C). The table specifies the conditions under which each scaling law applies, indicating the ‘bottleneck resource’ and the conditions when other resources are sufficiently large (’large resources’). Finally, it indicates where to find a rigorous proof for each scaling law including prefactor constants.
This table presents data for the multitask sparse parity problem used in the paper. It shows how each skill (parity task) is encoded in the control bits, the corresponding skill bits, and the relevant skill basis functions. The frequencies of the different parity tasks follow a power-law distribution, making this a challenging learning problem designed to study emergence and scaling laws in neural networks.
Full paper#