↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
High-dimensional data poses significant challenges for training and using diffusion models. Latent Diffusion Transformers (DiTs), while effective, suffer from quadratic computational complexity. This paper investigates the statistical and computational limits of DiTs, assuming data lies in a low-dimensional linear subspace. It examines the approximation error of using transformers for DiTs and analyzes the sample complexity for distribution recovery.
The researchers derive an approximation error bound for the DiTs score network and show its sub-linear dependence on latent dimension. They also provide sample complexity bounds and demonstrate convergence towards the original distribution. Computationally, they characterize the hardness of DiTs inference and training by establishing provably efficient criteria, demonstrating the possibility of almost-linear time algorithms. These findings highlight the potential of latent DiTs to overcome high-dimensionality issues by leveraging their inherent low-rank structure and efficient algorithmic design.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with latent diffusion transformers (DiTs). It offers theoretical insights into DiTs’ statistical and computational limits, paving the way for more efficient algorithms and providing guidance for their practical implementation. By addressing the high dimensionality challenge in generating data, this research is relevant to the current trend of developing scalable and effective generative AI models. It potentially opens new avenues for theoretical research in AI by characterizing the fundamental trade-offs between statistical accuracy and computational efficiency.
Visual Insights#

This figure illustrates the architecture of the DiT score network, which is a crucial component in latent diffusion transformers. It shows how the input data (x ∈ R^D) is processed through several layers to produce the score function estimate (sw(x,t)). The process involves a linear transformation to a lower-dimensional latent space (x ∈ R^d0), reshaping the latent representation for use in a transformer network (fT ∈ Tr,m,l), and a subsequent linear transformation back to the original data space before finally generating the score function.
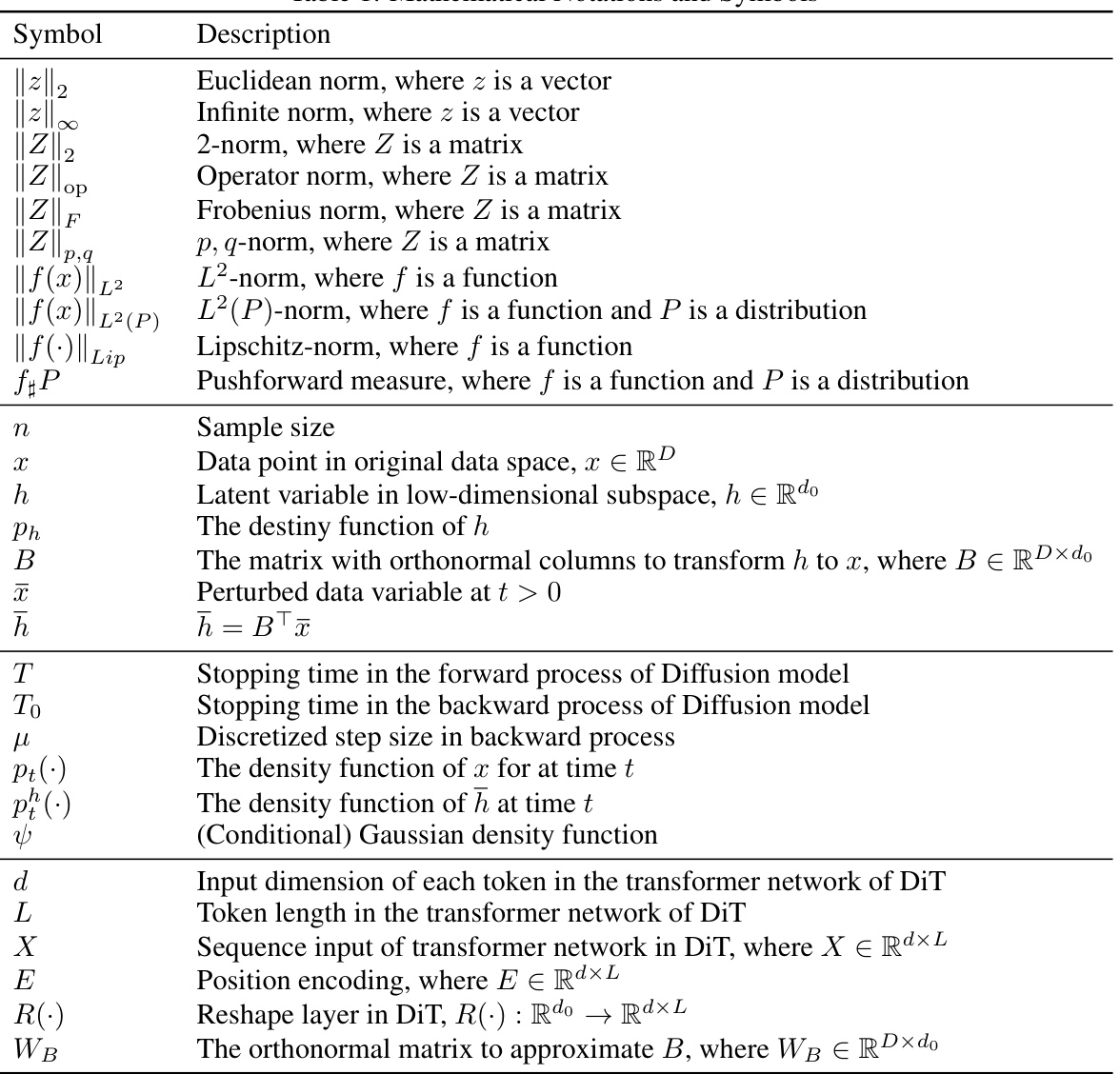
This table lists mathematical notations and symbols used in the paper, including norms (Euclidean, infinite, 2-norm, operator norm, Frobenius norm, p,q-norm), function norms (L2-norm, L2(P)-norm, Lipschitz-norm), and symbols representing data points, latent variables, time stamps, density functions, dimensions, and other parameters related to the Diffusion model and Transformer architecture.
Full paper#



















