↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Deep learning models’ optimization is often visualized using loss landscapes. While existing research primarily focuses on flat or sharp minima, this paper investigates an asymmetric valley shape. This asymmetry is often overlooked and its causes and effects aren’t fully understood, hindering improvements to deep learning methods.
This research systematically explores factors influencing this valley asymmetry, including dataset characteristics, network architecture, initialization methods, and hyperparameters. Key findings indicate that the sign consistency between added noise and the model’s convergence solution strongly affects valley symmetry. The paper presents theoretical explanations for this phenomenon using ReLU activation and softmax functions and proposes practical applications for model fusion and federated learning. This provides insight to improve model aggregation and parameter alignment by leveraging sign alignment, potentially boosting performance.
Key Takeaways#
Why does it matter?#
This paper is crucial because it unveils the hidden asymmetry in deep neural network loss landscapes, challenging existing assumptions about valley shapes. It offers novel theoretical insights and practical implications for model fusion and federated learning, opening up exciting new avenues for improving model training efficiency and generalizability. This has the potential to improve various deep learning applications.
Visual Insights#
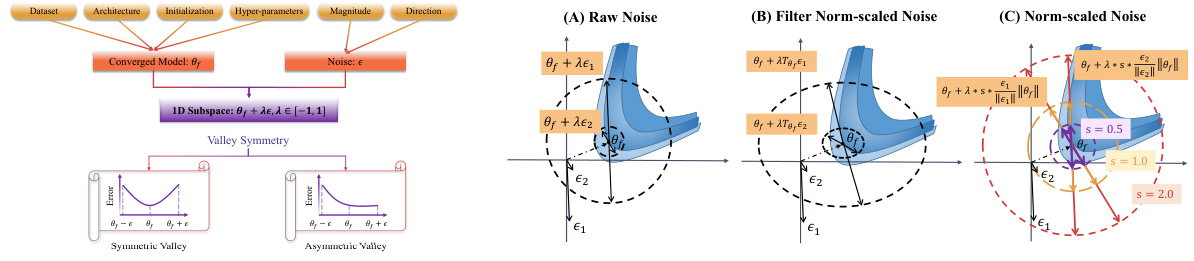
This figure illustrates the factors influencing the symmetry of deep neural network (DNN) loss valleys. It shows that valley symmetry is affected by both the converged model (θf) and the noise (e) added to it during 1D visualization (θf + λε, where λ is in [-1,1]). The factors influencing the converged model include dataset, architecture, initialization, and hyperparameters. Factors influencing the noise include magnitude and direction. Three types of noise visualization methods are shown: raw noise, filter norm-scaled noise, and norm-scaled noise. The norm-scaled method normalizes the noise magnitude while preserving its direction. The figure contrasts symmetric and asymmetric valleys, highlighting the crucial role of noise direction and its relationship with the converged model in determining valley symmetry. The sign consistency (or inconsistency) between noise and model parameters directly affects whether the valley appears symmetric or asymmetric.
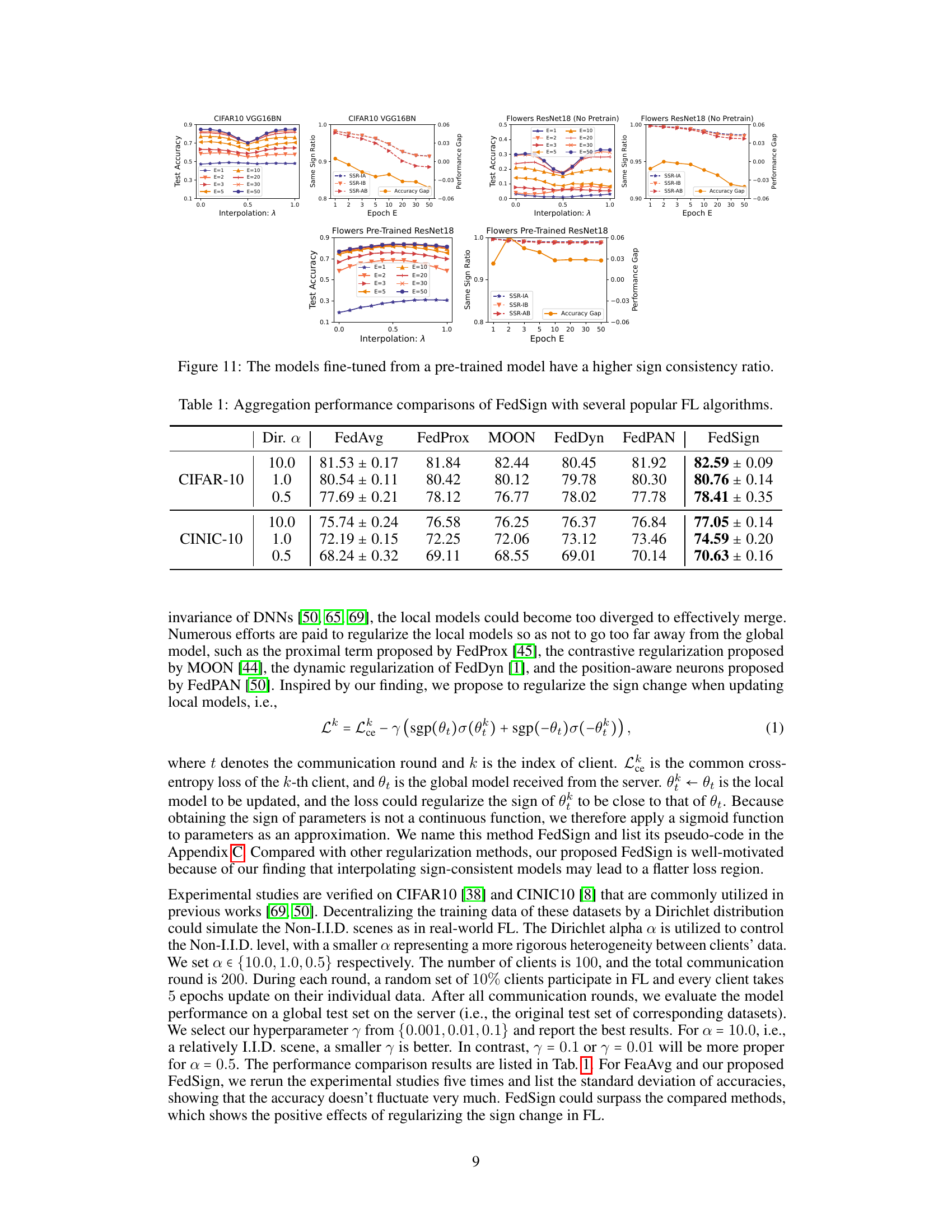
This table compares the performance of the proposed FedSign algorithm with other popular federated learning (FL) algorithms, including FedAvg, FedProx, MOON, FedDyn, and FedPAN. The comparison is done across two datasets, CIFAR-10 and CINIC-10, and under different levels of data heterogeneity (controlled by the Dirichlet distribution parameter α). The results are presented as accuracy ± standard deviation, showing the average performance across multiple runs. This table demonstrates the effectiveness of FedSign in achieving higher accuracy compared to other methods, particularly in scenarios with Non-IID data distributions.
In-depth insights#
Asymmetric Valleys#
The concept of “asymmetric valleys” in deep neural network loss landscapes challenges the traditional understanding of flat vs. sharp minima. Instead of symmetric valleys around minima, this research explores scenarios where the loss function exhibits different shapes along various directions. This asymmetry significantly influences the generalization ability of the network and optimization dynamics. Understanding and exploiting this asymmetry opens up new avenues for model fusion techniques and federated learning strategies, potentially improving performance and parameter alignment by focusing on sign consistency between noise and convergence solutions. The exploration of the factors influencing this asymmetry, like dataset properties, network architecture, and hyperparameters, is crucial. Further theoretical insights, potentially relating activation functions (like ReLU) and softmax to this phenomenon, will solidify our understanding. Ultimately, this analysis has significant implications for the development of more effective optimization algorithms and model aggregation methods.
Noise & Symmetry#
The interplay between noise and symmetry in deep neural network (DNN) loss landscapes is a complex and nuanced topic. Noise, often introduced through techniques like dropout or data augmentation, can significantly impact the optimization process. It can perturb the network’s weights, potentially leading it towards flatter minima, which are generally associated with better generalization. However, the type and magnitude of noise matter significantly. Gaussian noise, for instance, might have different effects compared to more structured or adversarial noise. Symmetry, or the lack thereof, in the loss landscape, also affects generalizability, as perfectly symmetric landscapes often signify that a model has an easier path to convergence and might not have learned nuanced decision boundaries. An asymmetric loss landscape, meanwhile, could indicate a more robust model that has successfully navigated intricate data features. The paper’s core contribution lies in its methodical exploration of asymmetric valleys, a less-studied area, revealing that the direction and sign consistency between the noise and the convergence point critically influence valley symmetry. This is crucial because it indicates that flatter regions in the loss landscape might not be uniformly distributed around a minima, challenging the commonly held assumptions of previous studies. This new understanding could lead to improved model fusion techniques and innovative training strategies.
Model Fusion#
The concept of ‘Model Fusion’ in the context of deep learning focuses on combining multiple models to improve performance or achieve other benefits. The paper explores this by examining the effect of sign consistency between models on the success of fusion. Sign consistency, meaning the agreement in the signs of model parameters, is identified as a crucial factor. High sign consistency between models facilitates effective interpolation and aggregation, leading to performance improvements. Model soups, where multiple models are averaged, are shown to be successful because of high sign consistency among their parameters derived from a common pre-trained model. This understanding is then leveraged to propose a novel regularization technique, FedSign, in federated learning. FedSign aims to align model parameters’ signs during federated training, thereby addressing the challenge of non-independent and identically distributed (non-IID) data and improving model aggregation in such scenarios. The findings highlight that sign alignment is a valuable approach for better model fusion, enabling more effective and robust deep learning applications.
ReLU & Softmax#
The ReLU (Rectified Linear Unit) and Softmax functions are crucial components in many deep neural networks, particularly in classification tasks. ReLU’s inherent asymmetry, where it outputs zero for negative inputs and a linear response for positive ones, plays a significant role in shaping the loss landscape. This asymmetry, when coupled with the softmax function’s normalization of outputs to a probability distribution, contributes to the complex, often asymmetric, nature of the valleys in the loss landscape. The paper explores how noise, specifically the sign consistency between noise and the converged model, interacts with ReLU and softmax to influence the symmetry of these valleys. The theoretical analysis suggests that sign-consistent noise is more likely to maintain the activation pattern established by ReLU, impacting the Hessian matrix and potentially leading to flatter valleys along those directions. Understanding the interplay of ReLU’s asymmetry and Softmax’s normalization, as mediated by noise direction, is key to explaining and potentially exploiting the asymmetric valley phenomenon.
Future Works#
The paper’s “Future Works” section would greatly benefit from addressing several key aspects. Formal mathematical proofs to support the observed asymmetric valley phenomenon are crucial, moving beyond the empirical observations presented. Extending the analysis beyond image classification to other domains (e.g., natural language processing, time series forecasting) is vital for establishing the generality of the findings. Investigating the interplay between network architecture and the asymmetric valley is also important, exploring how different architectural choices influence the valley’s shape and properties. Finally, the authors should explore practical applications of their insights, potentially improving optimization algorithms or enhancing model fusion techniques. Addressing these points would significantly strengthen the paper’s impact and contribute to a more robust understanding of the loss landscape in deep neural networks.
More visual insights#
More on figures
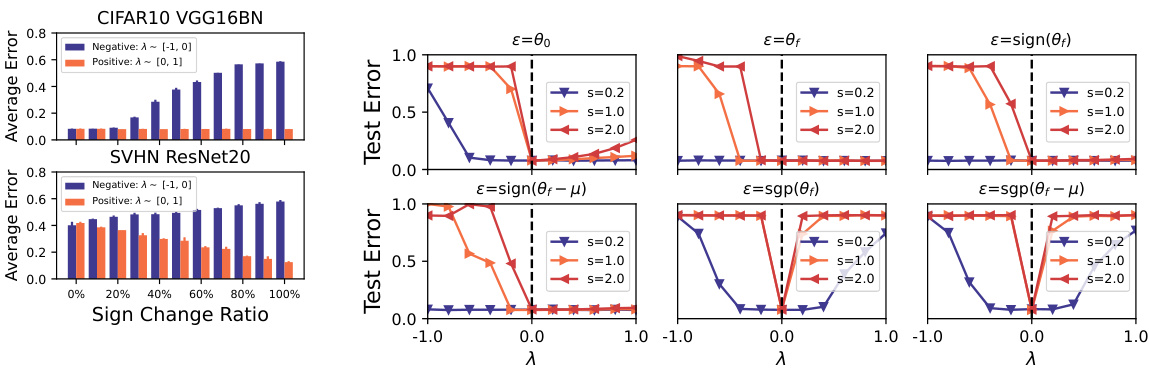
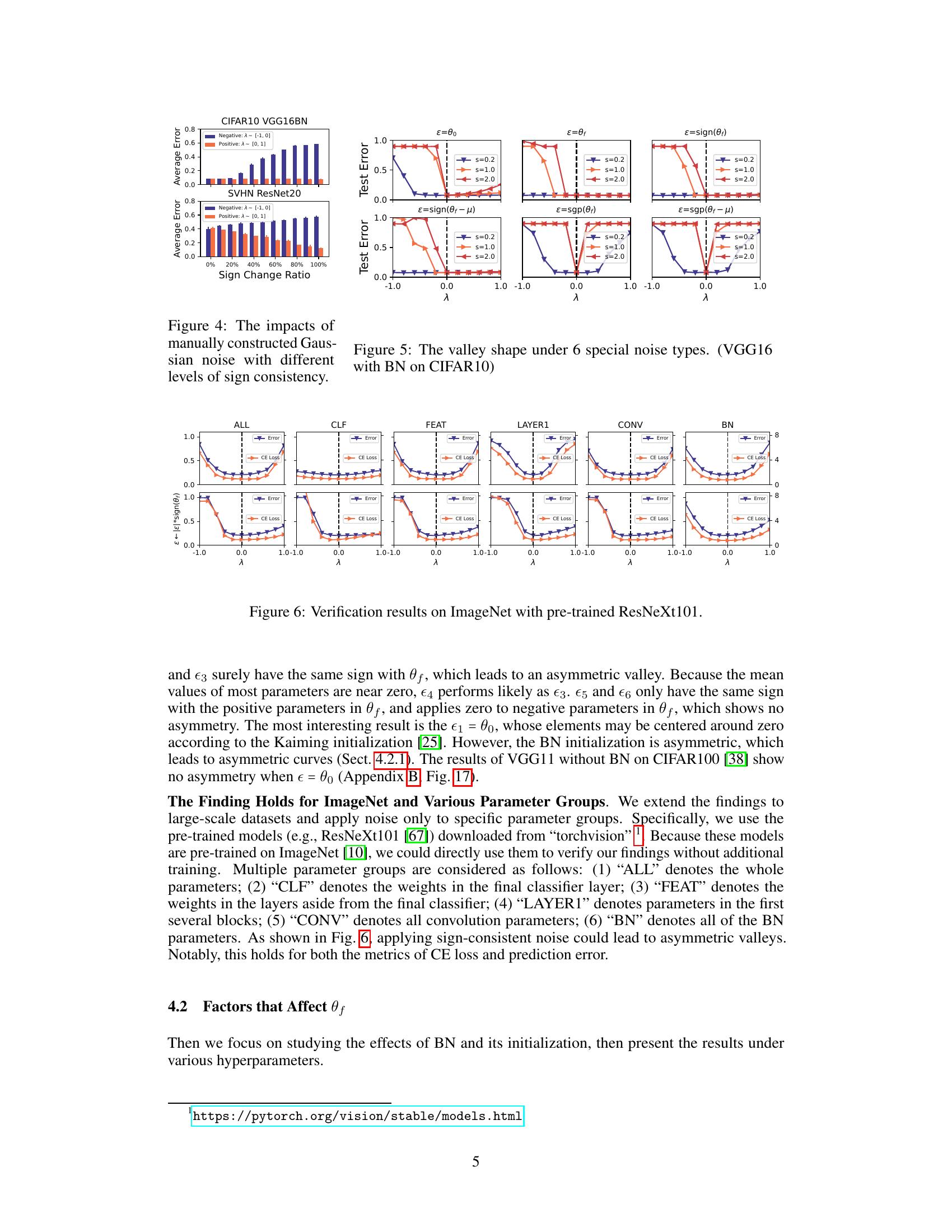
This figure shows the results of an experiment that manually controls the sign consistency between the noise and the converged model. The x-axis represents the ratio of elements in the noise that have their signs changed to match the converged model. The y-axis shows the average test error for positive and negative interpolations. As the sign change ratio increases, the test error of positive interpolations decreases, while the test error of negative interpolations increases, demonstrating the impact of sign consistency on the valley symmetry and flatness. The results are shown for two different datasets and network architectures (CIFAR10 VGG16BN and SVHN ResNet20) to illustrate generalizability.
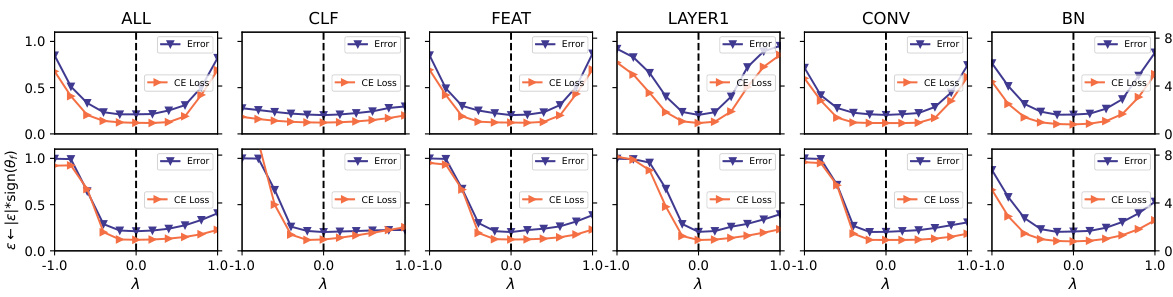
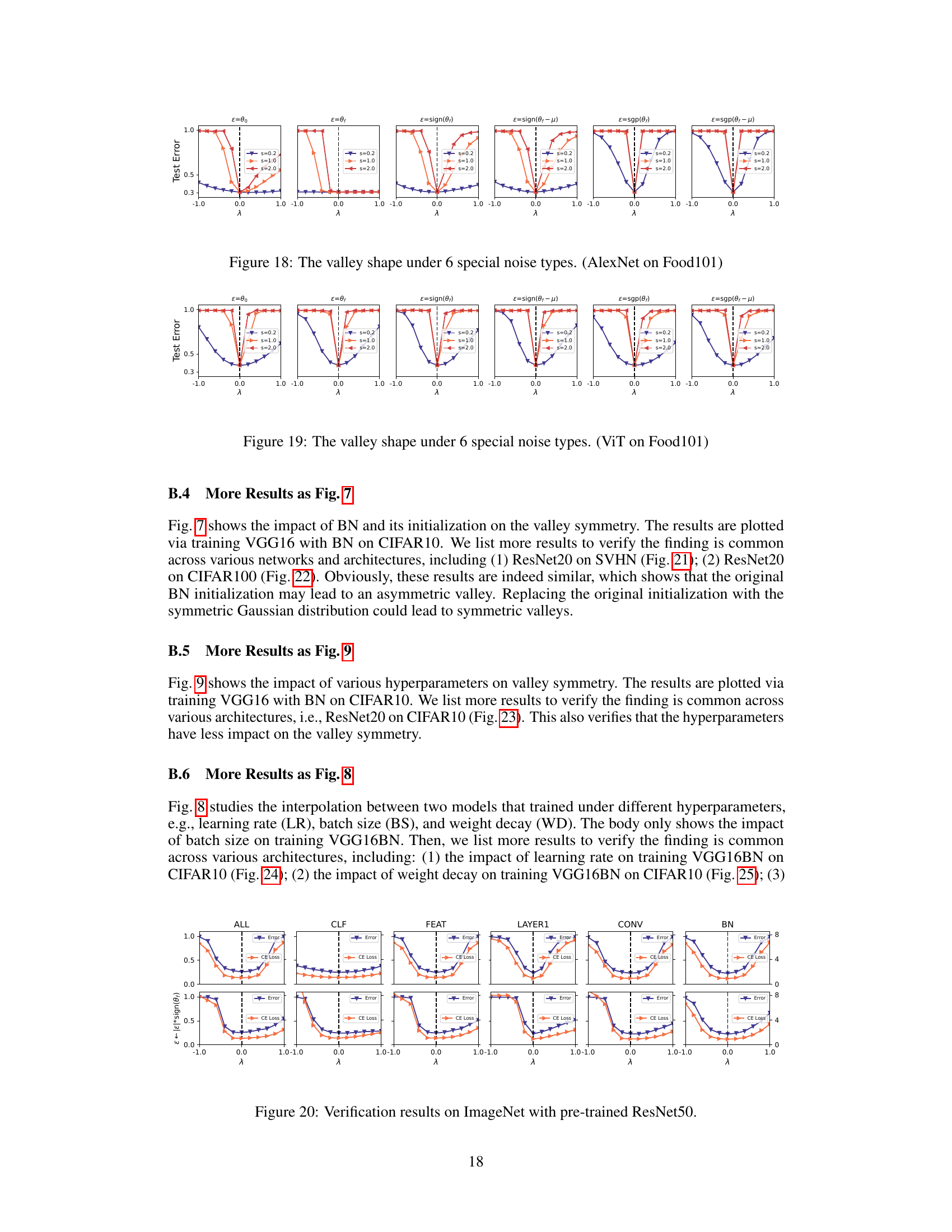
This figure shows the verification results on ImageNet using a pre-trained ResNeXt101 model. Different noise types were applied to different parameter groups (ALL, CLF, FEAT, LAYER1, CONV, BN), and the resulting valley shapes are shown for both the original noise and the noise with its sign replaced by the sign of the converged model. The results validate the authors’ finding that sign consistency between the noise and the converged model affects valley symmetry and flatness.
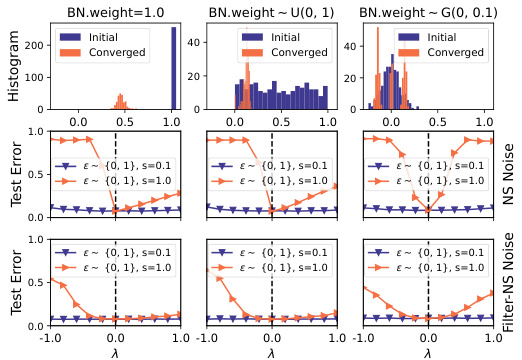
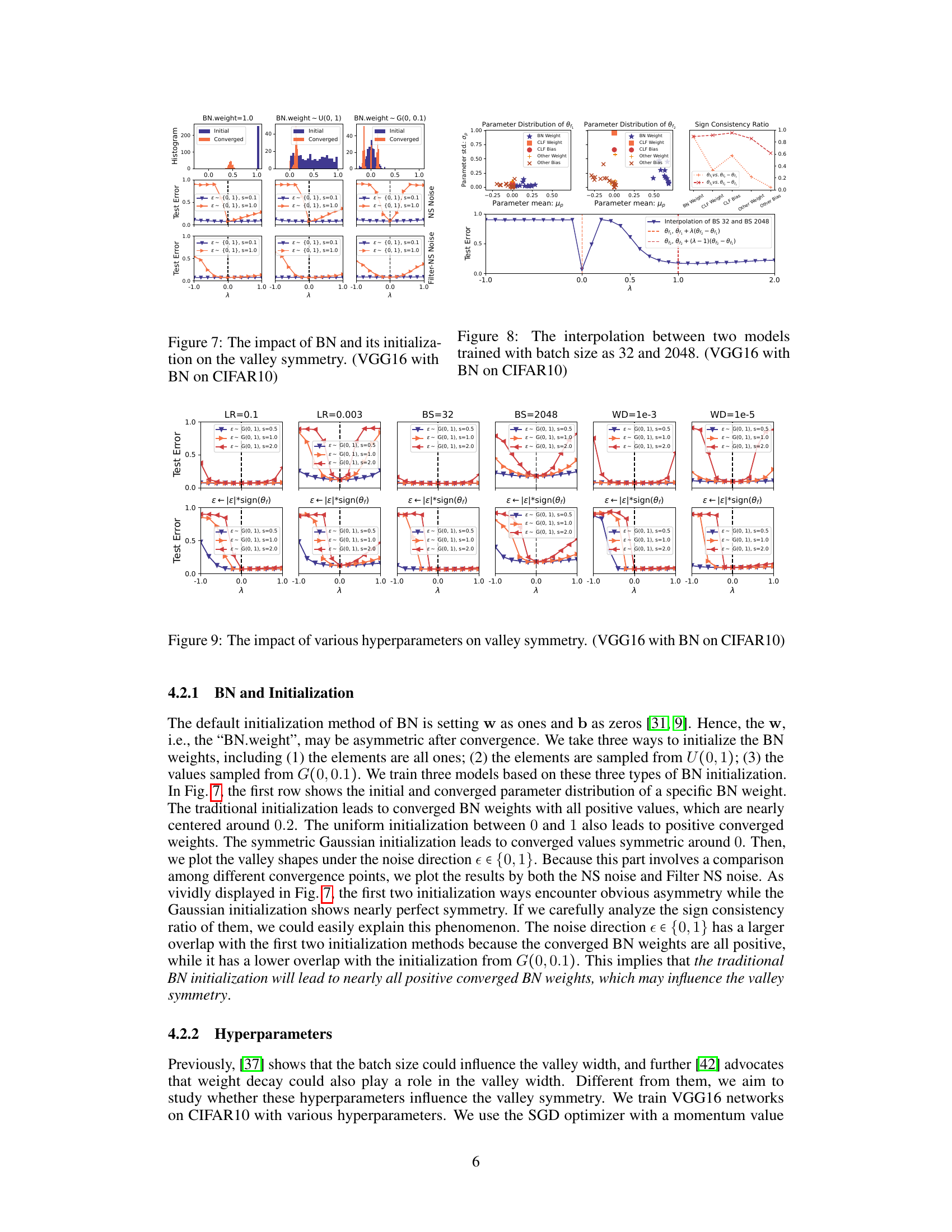
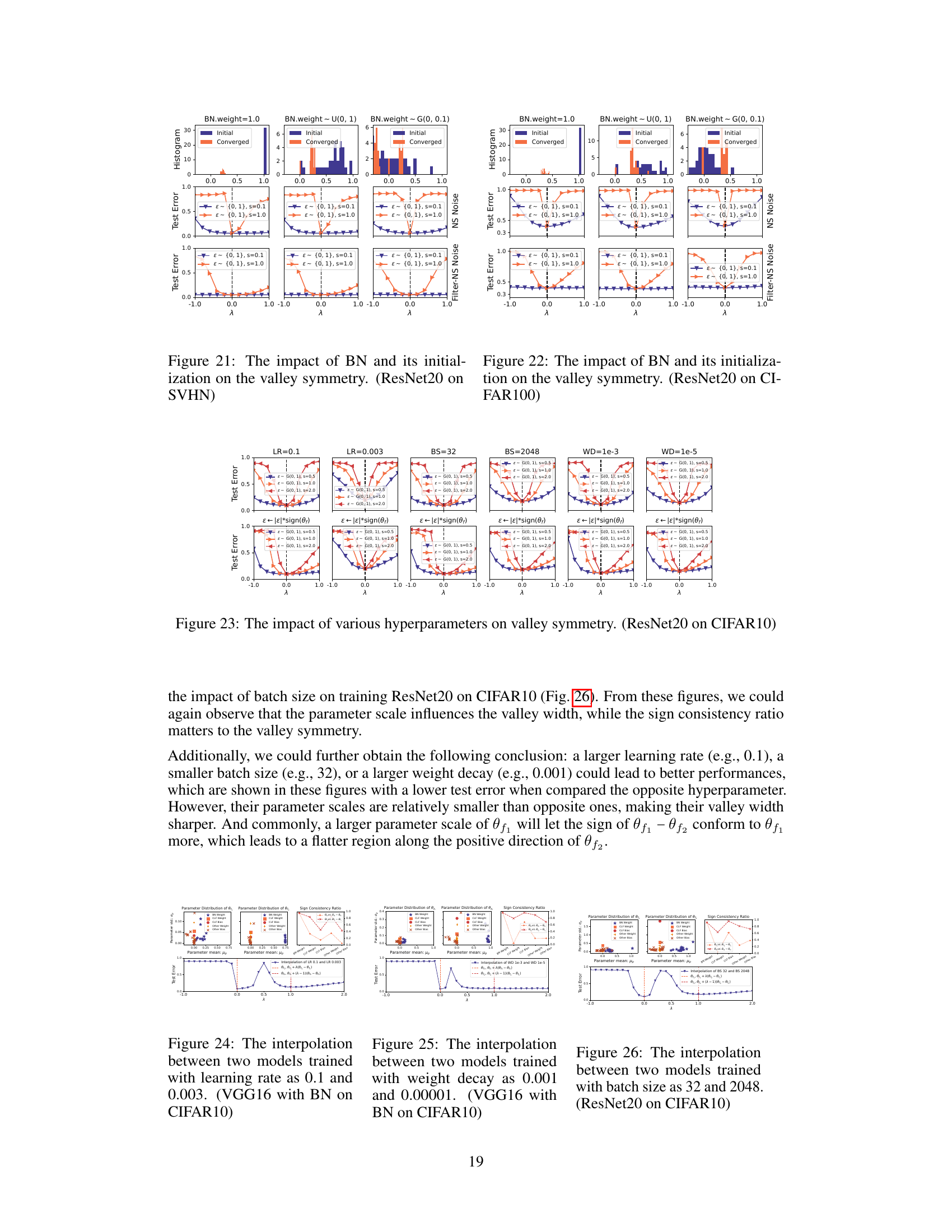
This figure visualizes how different initializations of Batch Normalization (BN) layers affect the symmetry of the loss landscape in deep neural networks. Three different initialization methods are used: setting BN weights to 1.0, sampling them from a uniform distribution U(0, 1), and sampling them from a Gaussian distribution G(0, 0.1). The resulting loss landscapes are shown using both the Norm-Scaled noise and the Filter-NS noise, visualizing the test error across a range of λ values. The histograms show the initial and converged distributions of the BN weights. The results demonstrate that the choice of BN weight initialization significantly impacts the valley’s symmetry. Specifically, the initializations with all positive weights (1.0 and U(0,1)) demonstrate clear asymmetry, whereas the Gaussian initialization leads to near-perfect symmetry.
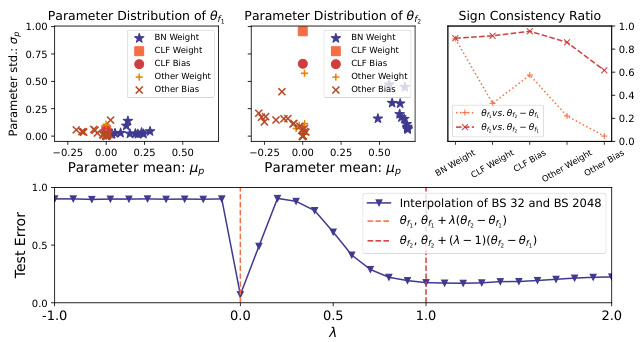
This figure visualizes the interpolation between two models trained with different batch sizes (32 and 2048). The left and center plots show the parameter distributions (mean and standard deviation) of the two models for different parameter groups (BN weights, classifier layer weights and biases, other weights and biases). The right plot shows the interpolation curve of the test error between the two models, demonstrating how the error changes as one varies the weights from one model to the other. The sign consistency ratio between the two models for each parameter group is also illustrated. This helps explain why interpolating between the models may be difficult due to discrepancies in the parameters, especially considering differences in their signs.
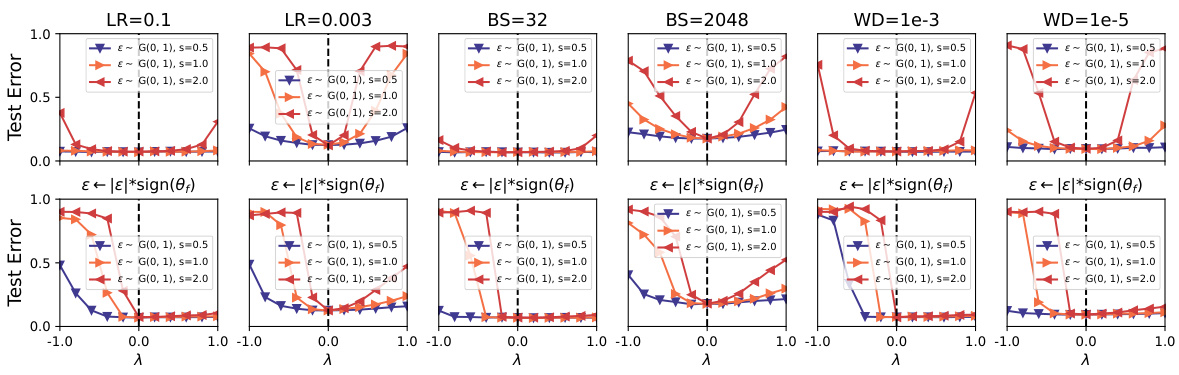
This figure visualizes the impact of different hyperparameters (learning rate, batch size, weight decay) on the valley symmetry of deep neural networks. It presents 1D interpolation plots of the loss landscape around a minimum, showing how the valley shape changes depending on the hyperparameter setting and whether the sign of the noise is consistent with the direction of the model parameters at convergence. The results suggest that the hyperparameters significantly affect the valley width, but don’t alter its symmetry.
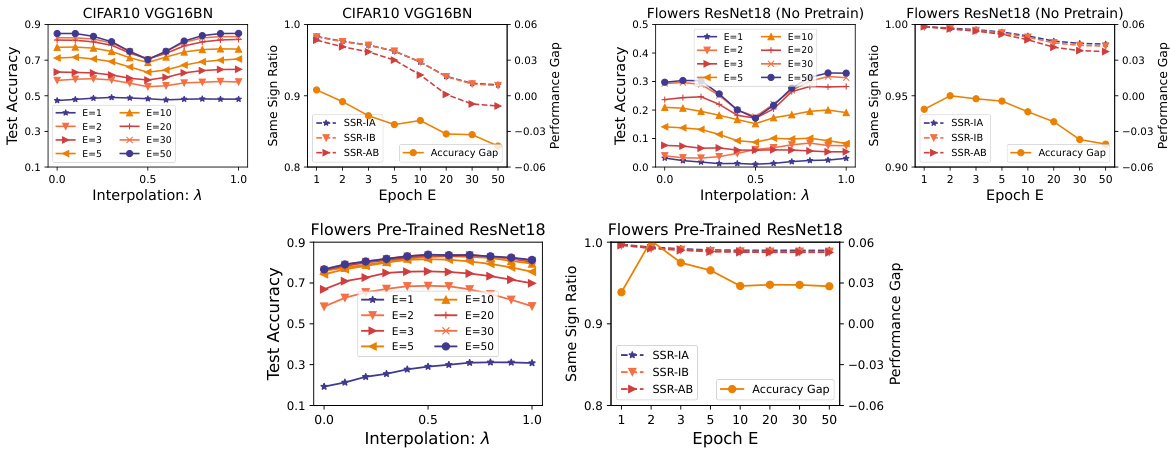
This figure visualizes the relationship between model interpolation performance and sign consistency ratio for two datasets: CIFAR10 with VGG16BN and Flowers with ResNet18. It shows interpolation accuracy and performance gap (difference between interpolation and average individual model accuracy) against the interpolation parameter lambda. Separate plots show the same sign ratio (SSR) between the two models’ parameters across three different measures (SSR-IA, SSR-IB, SSR-AB), as well as the ratio’s evolution over different training epochs. The key finding is that models fine-tuned from pre-trained models exhibit higher sign consistency, which correlates with better interpolation performance. The contrast between randomly initialized and pre-trained models highlights the influence of pre-training on the sign consistency and its effects on model fusion.
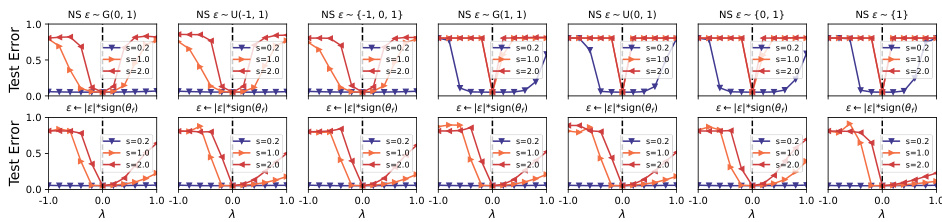
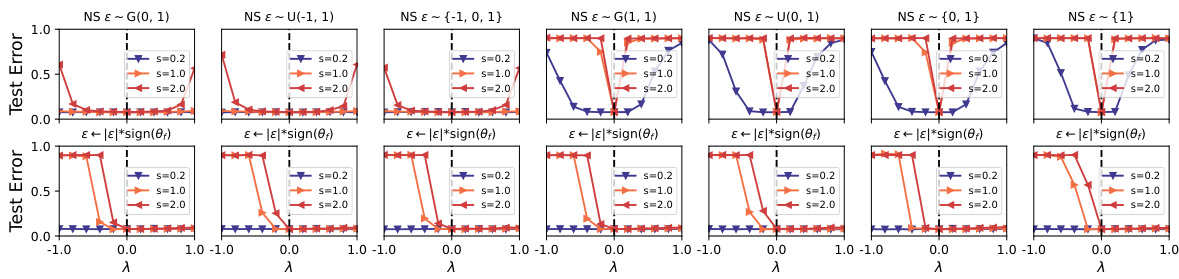
This figure displays the results of 1D valley visualization using different noise types. The first row shows results using seven common noise distributions (Gaussian, uniform, etc.) applied to a VGG16 network trained on CIFAR10 dataset. The second row shows the same experiment, but this time the sign of the noise is flipped to match the sign of the converged model parameters. The figure demonstrates that the sign consistency between noise and converged model plays a crucial role in determining the valley’s symmetry.
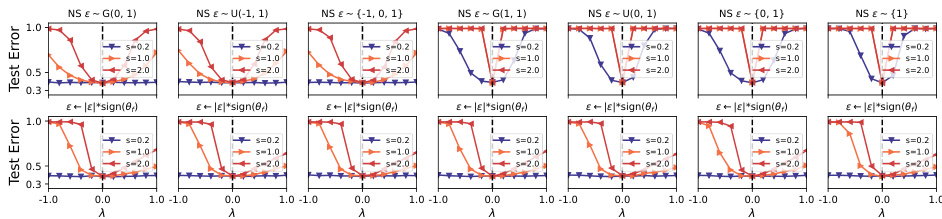
This figure visualizes the loss landscape of a VGG16 network with Batch Normalization (BN) trained on the CIFAR-10 dataset. The top row displays the loss curves for seven different noise types added to the converged model parameters (θf). Each curve represents the loss along a 1D subspace defined by θf + λε, where λ varies from -1 to 1 and ε is a normalized noise vector. The bottom row shows the same experiment but with the sign of the noise vector flipped to match that of the converged model parameters. The comparison highlights the effect of noise direction and sign consistency on the valley’s symmetry (or asymmetry). The results demonstrate that sign consistency between noise and converged solution is a critical factor for valley asymmetry.
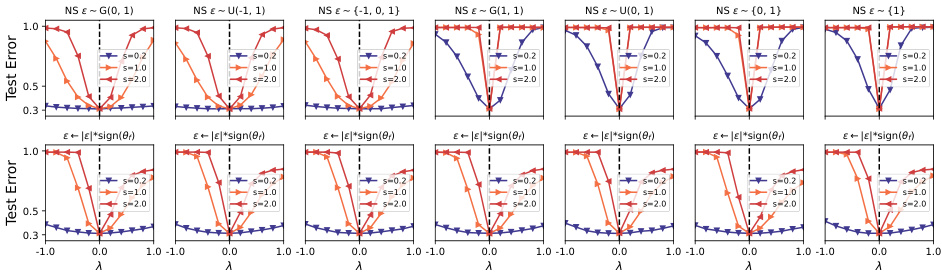
This figure visualizes the loss landscape of a VGG16 network with batch normalization (BN) trained on the CIFAR-10 dataset. The top row shows the loss curves along seven different noise directions, demonstrating nearly symmetric valleys. The bottom row shows the loss curves when the noise sign is flipped to match the sign of the converged model (θf). This manipulation results in pronounced asymmetric valleys, illustrating how noise direction significantly influences the loss landscape’s symmetry. The asymmetry is particularly prominent when the noise direction aligns with the direction of the converged model.
This figure visualizes the loss landscape of a VGG16 network with Batch Normalization (BN) trained on the CIFAR-10 dataset. The top row shows the loss curves obtained using seven different types of noise added to the model parameters. The bottom row shows the effect of flipping the sign of the noise vectors before adding them. The figure demonstrates that the sign consistency between the noise and the model parameters significantly impacts the valley symmetry, resulting in asymmetric valleys when the signs are flipped.

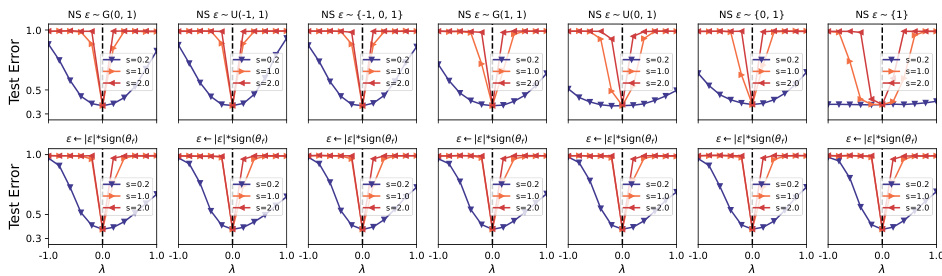
This figure shows the loss landscape of a VGG16 network trained on CIFAR10 with batch normalization, along six different noise directions. Each plot shows the test error as a function of lambda (λ), ranging from -1 to 1, with various noise scaling factors (s). The noise directions used are intended to explore different aspects of the model’s parameter space and its relationship to the loss landscape, aiming to demonstrate the effect of noise direction on the shape of the loss valleys and how it relates to the sign consistency between the noise and the converged model.

This figure shows the loss landscape of a VGG16 network with batch normalization trained on CIFAR10, along six different noise directions. Each plot represents a 1D interpolation of the loss function, where the starting point is the model’s converged parameters (θf), and the interpolation direction is determined by one of six noise vectors. The noise vectors are: the initialization before training (ε = θ0), the converged model itself (ε = θf), the sign of the converged model (ε = sign(θf)), the sign of the converged model minus its mean (ε = sign(θf − μ)), and the sign and non-sign of the converged model (ε = sgp(θf), ε = sgp(θf − μ)). The plots display the test error with different widths (s = {0.2, 1.0, 2.0}) along each noise direction. The results illustrate the impact of noise direction on the symmetry of the valley, which contributes to the asymmetric valley phenomenon discussed in the paper.

This figure displays the loss landscape of a VGG16 network with batch normalization trained on CIFAR-10 dataset, but with variations in the noise vectors used for 1D interpolation. Six different types of noise vectors are shown, each impacting the valley symmetry differently. The results highlight the effect of noise direction and magnitude on the observed shape of the loss valley, thereby supporting the paper’s claims about the relationship between noise characteristics, valley symmetry, and model convergence.

This figure visualizes the loss landscape of a VGG16 network with batch normalization trained on CIFAR10 along six different noise directions. Each subfigure represents a 1D interpolation of the loss function starting from a local minimum (θf) and moving in a direction defined by a specific noise vector (ε). The noise vectors are designed to investigate the impact of various noise characteristics on the symmetry of the loss landscape. The different types of noise vectors include: the initialization before training (θ0), the converged model itself (θf), the sign of the converged model (sign(θf)), the sign of the converged model minus the mean value of each parameter group (sign(θf - μ)), the sign of each element of the converged model (sgp(θf)), and the sign of each element of the converged model minus the mean value of each parameter group (sgp(θf-μ)). The resulting curves illustrate how these different noise directions can lead to valleys with varying degrees of symmetry, demonstrating the effect of the noise direction on valley shape.
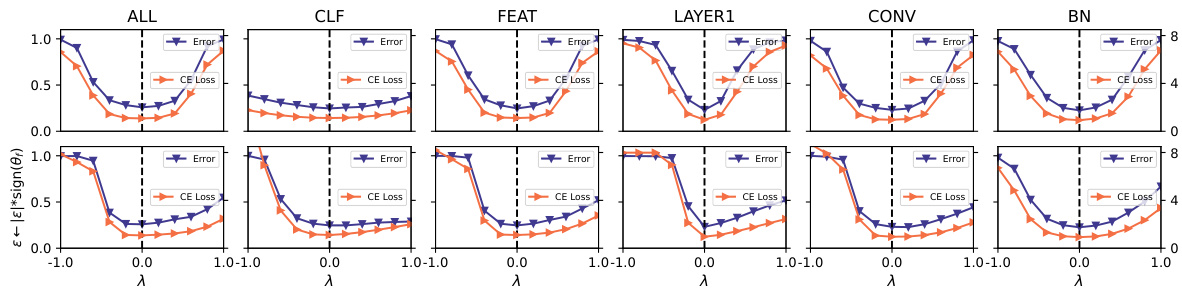
This figure displays the results of applying the sign-consistent noise to different parameter groups of a pre-trained ResNeXt101 model on the ImageNet dataset. It visually confirms that sign consistency between the noise and the converged model parameters is a key factor in determining valley asymmetry, as indicated by consistently flatter valleys in the positive direction for all parameter groups tested.
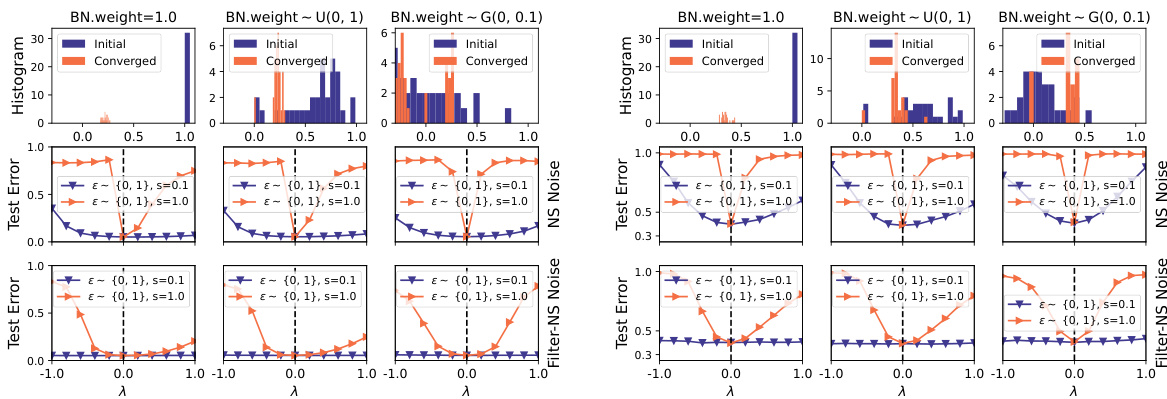
This figure shows how different initializations of Batch Normalization (BN) weights affect the symmetry of the loss landscape. Three different methods are used: all ones, uniform distribution between 0 and 1, and a Gaussian distribution with mean 0 and standard deviation 0.1. The top row displays the distributions of the BN weights initially and after convergence for each initialization method. The bottom rows show the 1D loss curves generated using two noise types (Norm-Scaled and Filter-Norm-Scaled) with different scaling factors, further illustrating the resulting valley shapes for each initialization. The results reveal a strong correlation between the BN initialization and valley symmetry, with the Gaussian initialization showing almost perfect symmetry and the other methods leading to asymmetry.
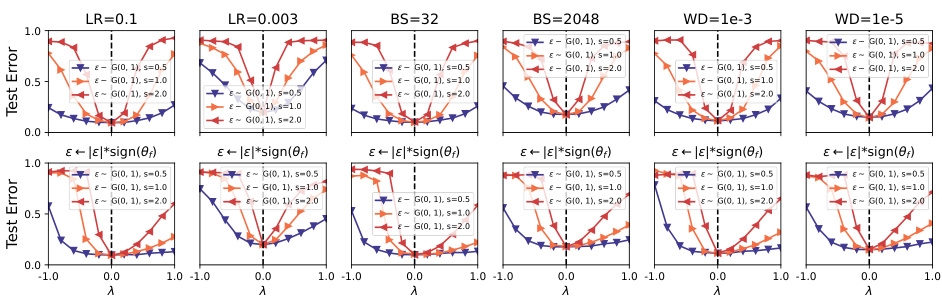
This figure shows the impact of various hyperparameters (learning rate, batch size, and weight decay) on the symmetry of the loss landscape valleys. It presents the results of 1D interpolation along both noise and sign-consistent noise directions under different hyperparameter settings, illustrating how changes in these parameters affect the flatness and symmetry of the loss landscape.

This figure displays the verification results on ImageNet using a pre-trained ResNeXt101 model. It shows the valley shape under different noise directions for various parameter groups within the model. The groups include all parameters, classifier weights and biases, feature extraction weights, parameters from the first layer(s), and convolution and Batch Normalization (BN) parameters. The results are presented to confirm the findings of the study, demonstrating how sign consistency between noise and converged models affects valley shape on a different dataset and with different parameter sets.
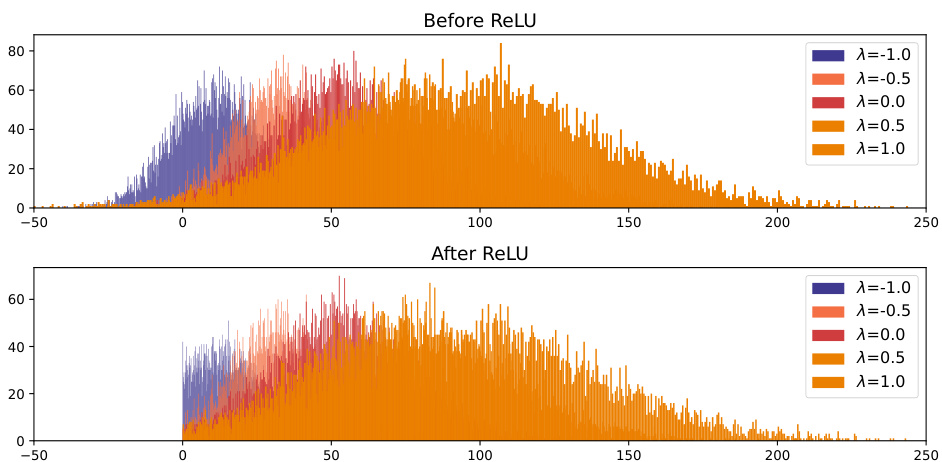
The figure shows the distribution of (w + λ * sign(w))Th for different values of λ, where w is a weight vector, h is a hidden representation vector, and δ is a random Gaussian vector. The distributions are plotted before and after applying the ReLU activation function. The experiment aims to demonstrate how the distribution shifts as λ changes, and to illustrate how ReLU non-linearity impacts the distribution, which is relevant to the paper’s exploration of the asymmetric valley in deep neural networks. The shift is more pronounced after the ReLU.

This figure shows the activation confusion matrix for different interpolation values (λ) between a converged model (θf) and its sign-consistent noise (|e|sign(θf)). The sum of diagonal values represents the agreement between the activations of the original model and the interpolated model. The figure demonstrates that the agreement is higher for positive λ values (sign consistency) than for negative λ values.
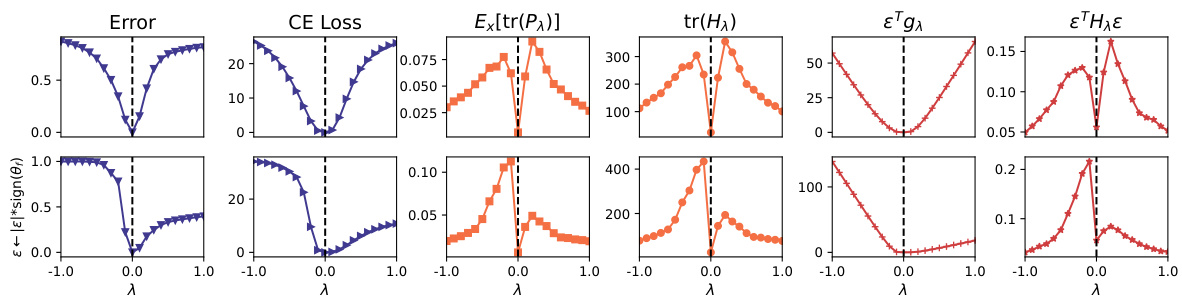
This figure displays several metrics calculated during a simple softmax classification demonstration. The top row shows metrics for a standard noise perturbation, and the bottom row shows the same metrics with sign-consistent noise. The metrics include: prediction error, cross-entropy loss, the average trace of a matrix (Px), the trace of the Hessian matrix (Hx), the first-order approximation of the loss (εTgλ), and the second-order approximation of the loss (εTHλ ε). The comparison highlights the effect of sign-consistent noise on the shape of the loss landscape, indicating that sign-consistent noise leads to a flatter loss landscape in the positive direction.
More on tables
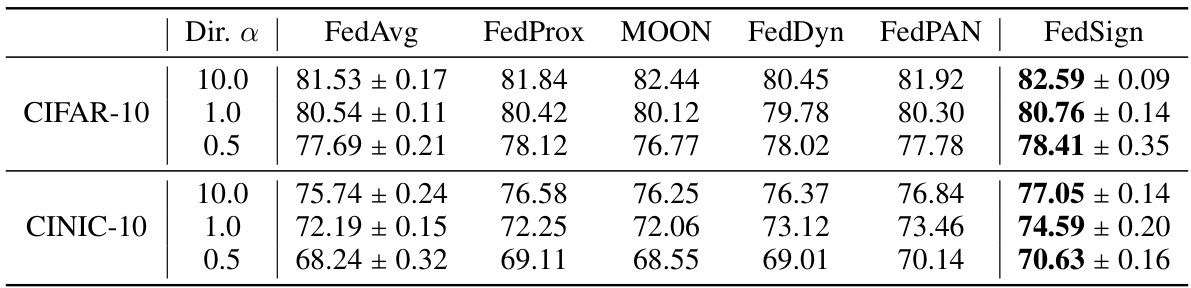
This table presents a comparison of the performance of FedSign, a novel federated learning algorithm proposed in the paper, against several other popular federated learning algorithms. The algorithms are evaluated on two benchmark datasets, CIFAR-10 and CINIC-10, with varying levels of data heterogeneity (controlled by the parameter α). The results show the accuracy achieved by each algorithm across different settings, allowing for a direct comparison of their relative effectiveness in handling Non-IID data and improving model aggregation in federated learning scenarios. FedSign consistently shows improvement over other algorithms.

This table compares the performance of the proposed FedSign algorithm against other popular federated learning (FL) algorithms. The comparison is done across two datasets (CIFAR-10 and CINIC-10) with varying levels of data heterogeneity (controlled by the parameter ‘Dir. α’). The results show the accuracy achieved by each algorithm, providing a quantitative assessment of FedSign’s effectiveness in the context of FL model aggregation.
Full paper#