↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many existing world models struggle to represent how actions systematically affect the environment’s state, leading to less predictable dynamics and hindered reinforcement learning (RL) performance. This often results in issues with planning and generalization in complex or noisy scenarios. Current models lack ways to represent coherent, predictable action effects.
The Parsimonious Latent Space Model (PLSM) tackles this by minimizing the mutual information between latent states and how actions change those states. This makes the model ‘softly state-invariant’, resulting in more predictable dynamics. Experiments demonstrate PLSM’s efficacy in various RL benchmarks, showing improvements in planning, model-free control, and generalization, especially in noisy conditions. The results highlight the importance of systematic action representation for effective world modeling.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel approach to simplifying latent dynamics in world models, leading to improved accuracy, generalization, and performance in various downstream tasks. It addresses a critical challenge in reinforcement learning by making the effects of actions more predictable. The proposed method opens up new avenues for research in model-based and model-free reinforcement learning, particularly in complex and noisy environments. It also highlights the importance of systematically considering the effects of actions when designing world models, paving the way for more efficient and robust AI systems.
Visual Insights#

This figure provides a high-level overview of the Parsimonious Latent Space Model (PLSM) and its application in various reinforcement learning scenarios. It illustrates how PLSM, combined with different model classes (Contrastive World Models, Self-Predictive Representations), improves performance across multiple tasks such as model-free RL (Atari), continuous control (DeepMind Control Suite), and control with visual distractions. The figure showcases the architecture’s components (encoder, query network, and dynamics), along with performance results demonstrated through graphs.

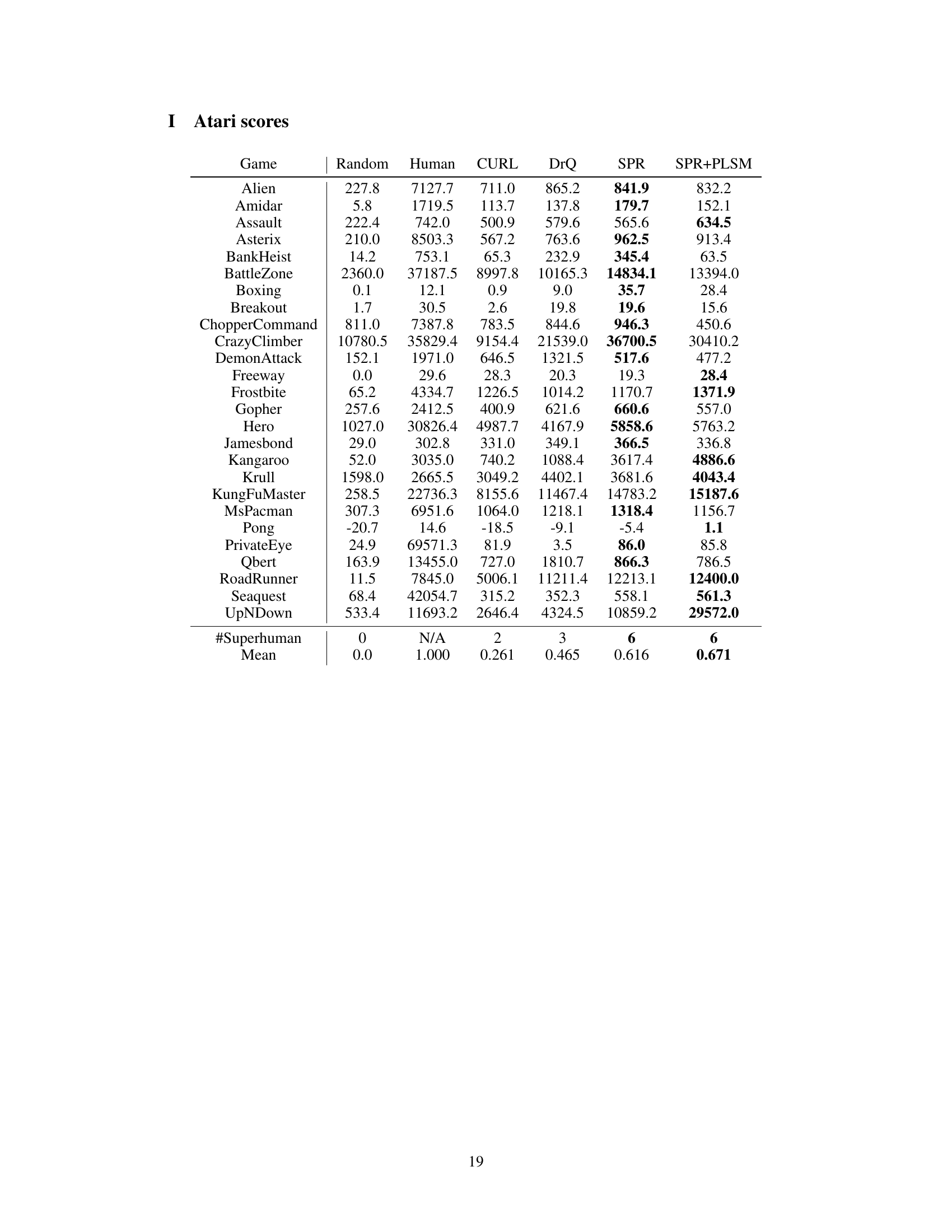
This table presents the accuracy of latent prediction at a horizon of 10 timesteps for two models: PLSM with slots and C-SWM. PLSM demonstrates a higher accuracy with a smaller standard error, indicating improved performance and reliability in long-horizon prediction for the Cubes 9 dataset.
In-depth insights#
Softly State-Invariant Models#
The concept of “Softly State-Invariant World Models” presents a novel approach to simplifying latent dynamics in reinforcement learning. The core idea revolves around reducing the dependence of predicted state transitions on the current latent state, making the effects of actions more predictable and systematic. This is achieved by minimizing the mutual information between the latent state and the change induced by an action. This regularization doesn’t enforce complete state invariance, allowing for necessary state-dependent dynamics, but encourages a more parsimonious representation where actions consistently produce similar effects across similar states. The benefits are significant, leading to improved accuracy, generalization across different tasks, and enhanced performance in both model-based and model-free reinforcement learning settings. The effectiveness of this approach is demonstrated through various experiments across diverse tasks, highlighting the importance of incorporating systematic action effects into world models for improved learning and control.
Parsimonious Latent Dynamics#
The concept of “Parsimonious Latent Dynamics” centers on simplifying how actions influence a system’s latent state. It suggests that efficient world models should prioritize representing the systematic effects of actions, minimizing the dependence of these effects on the current latent state. This approach emphasizes predictability and reduces the complexity of the model by making the latent dynamics more consistent across different states. The core idea is to create a soft state-invariance where actions have relatively predictable effects, regardless of the precise starting state, thereby improving the model’s generalization and robustness. Achieving parsimonious latent dynamics could involve techniques like minimizing mutual information between the latent state and the change caused by an action, effectively creating a bottleneck on the information flow. This leads to more concise and generalizable representations of the system’s behavior, ultimately improving performance in downstream tasks such as planning and control.
RL Benchmark#
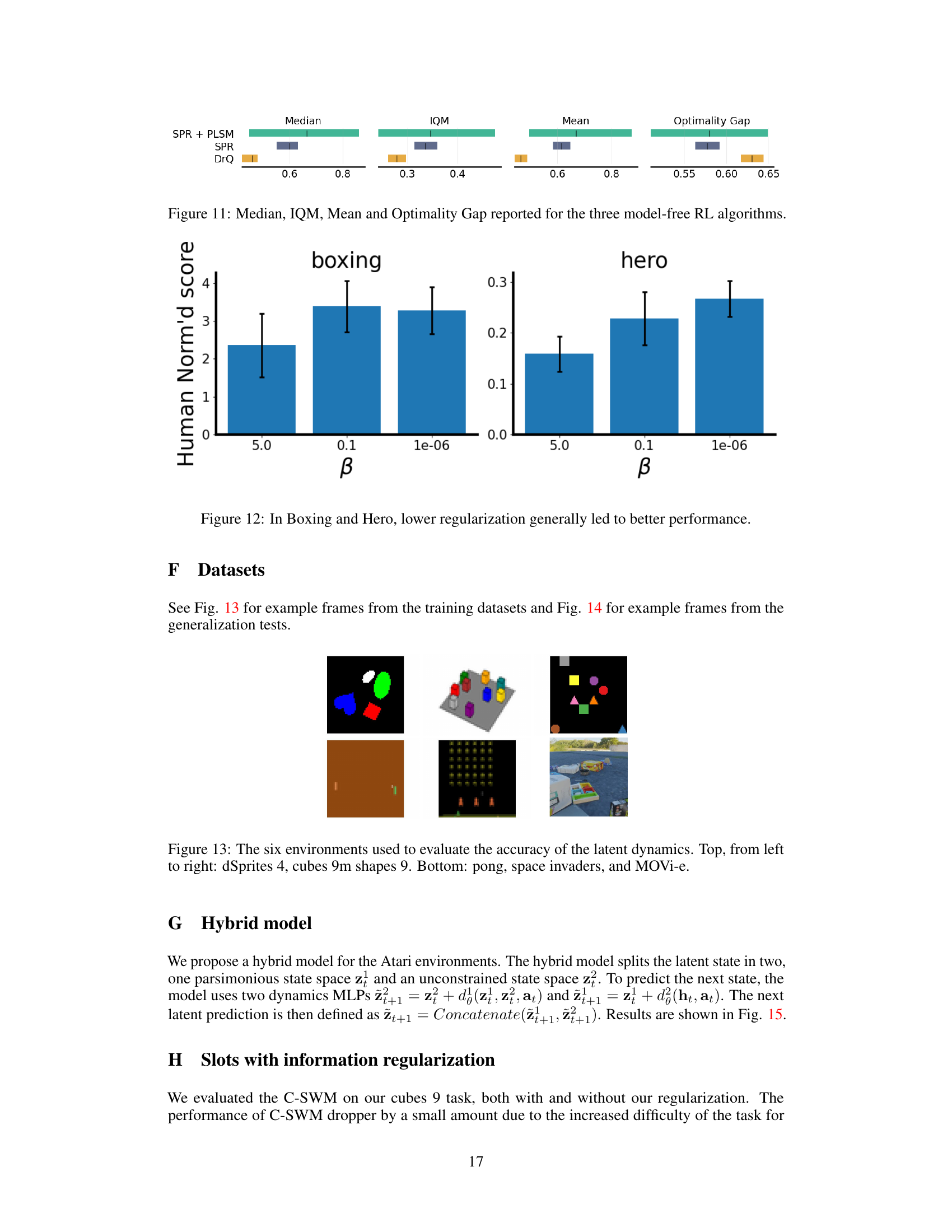
An RL benchmark section in a research paper would ideally present a systematic evaluation of the proposed reinforcement learning (RL) algorithm across diverse and challenging environments. This would involve selecting established benchmark tasks that are representative of the problem domain and comparing performance against state-of-the-art methods. Key aspects to consider are the metrics used for evaluation (e.g., average cumulative reward, sample efficiency, generalization performance), the experimental setup (e.g., hyperparameter tuning, training duration, random seeds), and detailed results that support the claims made. A robust benchmark would include error bars to show confidence intervals, demonstrating statistical significance. The choice of benchmarks themselves is crucial. A good benchmark will include a mix of continuous and discrete control tasks, simple and complex environments, and tasks with different levels of difficulty to illustrate the algorithm’s adaptability and performance limitations. Furthermore, it should analyze the qualitative aspects of the learned policies such as whether the agent exhibits emergent behaviors, demonstrates robustness to unforeseen situations, or displays efficient exploration strategies. The benchmark’s thoroughness and the quality of the analysis directly impact the credibility and significance of the research findings.
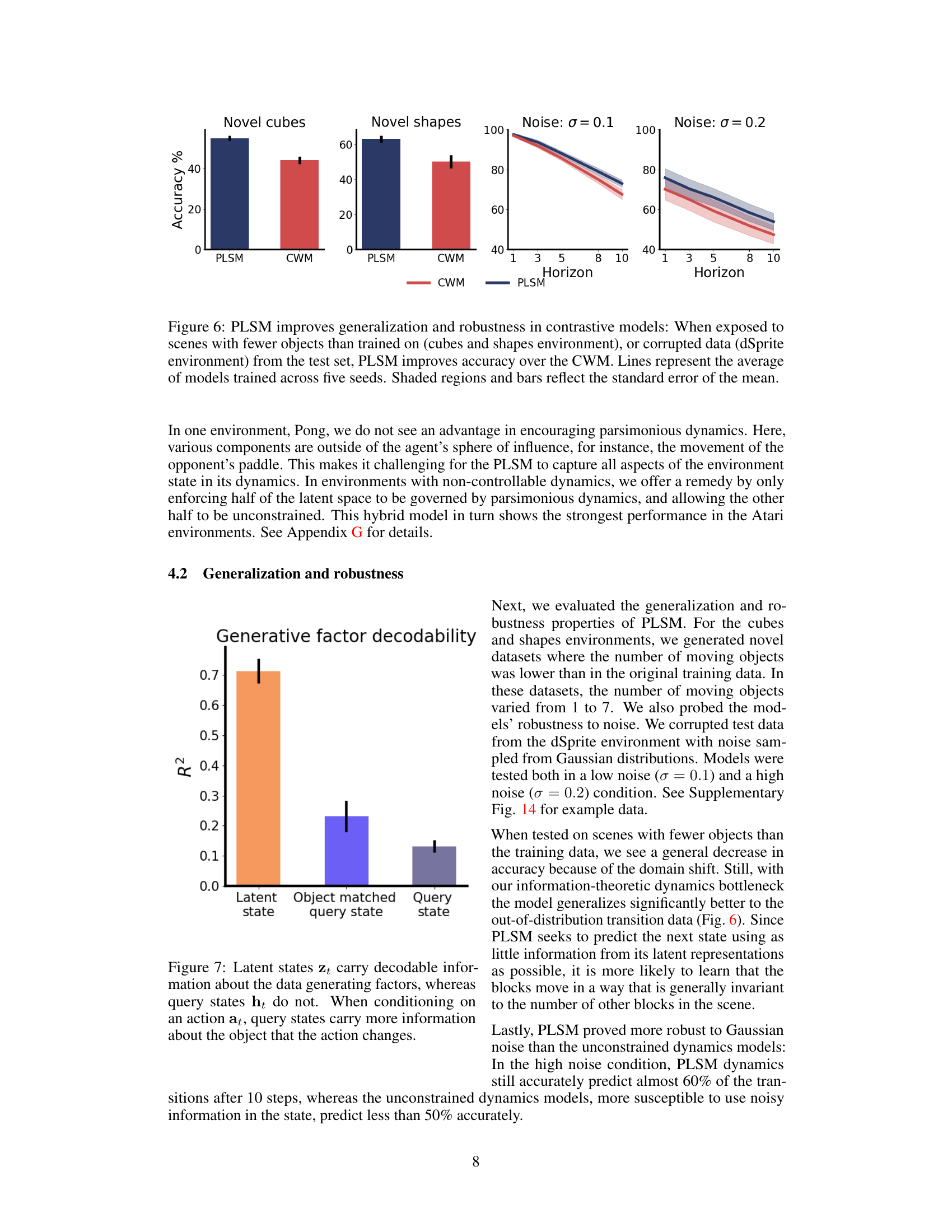
Generalization & Robustness#
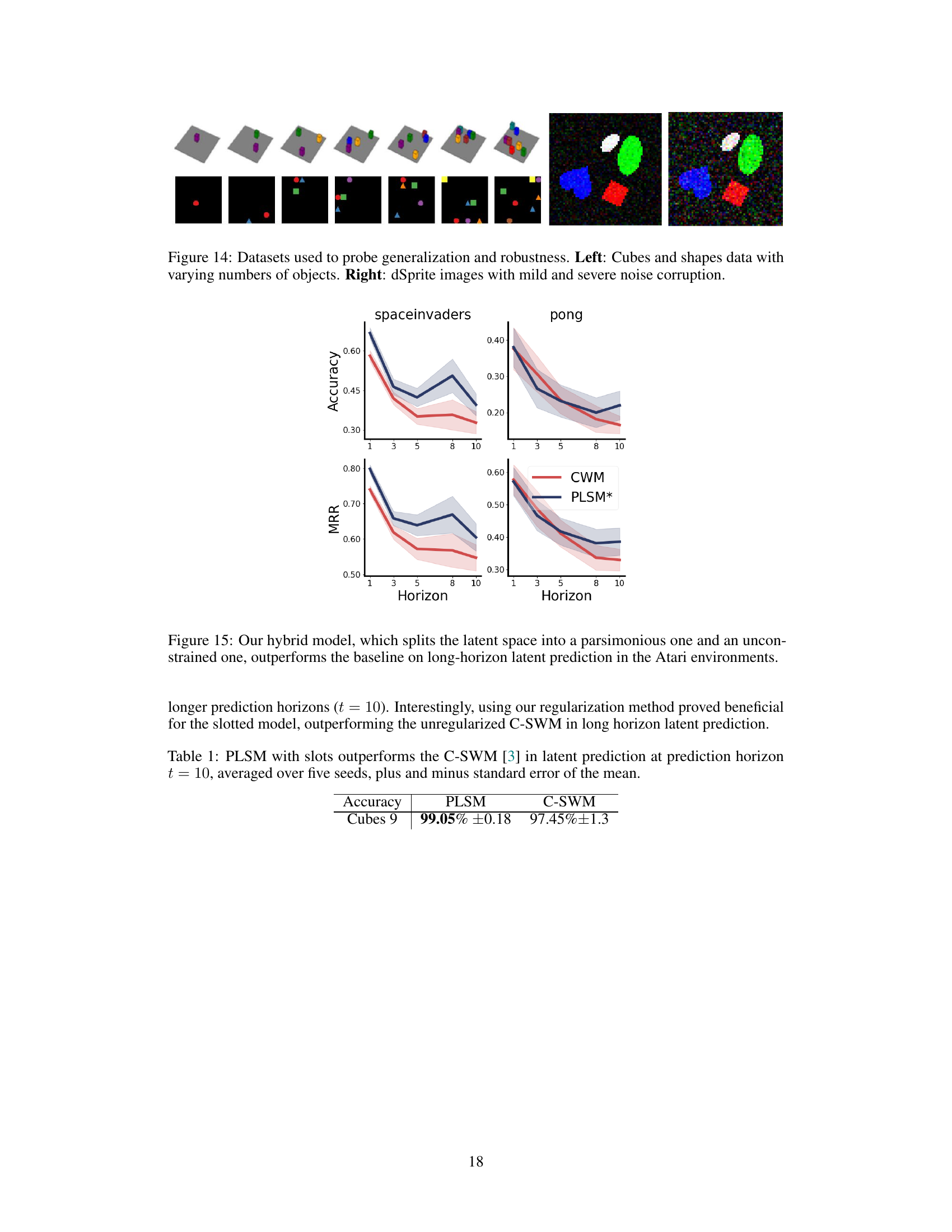
The section ‘Generalization & Robustness’ would explore the model’s ability to handle unseen data and noisy inputs. A key aspect would be evaluating performance on datasets with varying numbers of objects or levels of noise, compared to the training data. This assesses the model’s ability to generalize beyond its training distribution and its resilience to imperfections in real-world data. The results might show that the model retains accuracy even when encountering novel situations or corrupted data, suggesting robustness in the face of uncertainty. Alternatively, if the model’s performance suffers significantly under these conditions, this highlights a limitation in its generalization capability. A detailed analysis of these results, explaining why the model generalizes or fails to do so, provides valuable insights into its strengths and weaknesses. Specific metrics and visualizations might include accuracy rates, error bars and comparisons with baseline models, offering quantitative evidence for the model’s generalization and robustness.
Future Work#
The paper’s “Future Work” section would ideally explore several promising avenues. Extending the PLSM framework to handle recurrent dynamics and non-Markovian environments is crucial for real-world applications where agent history significantly influences actions. Investigating different regularization techniques beyond L2 norm penalization could enhance the model’s robustness and flexibility. A thorough comparison of PLSM with other state-of-the-art methods, including those addressing similar challenges like systematic action representation or soft state-invariance, is warranted to fully establish its strengths and limitations. Furthermore, exploring the hybrid model further and analyzing when it’s most beneficial (compared to purely parsimonious or unconstrained models) is necessary. Finally, conducting experiments in more complex and diverse environments and scaling up to high-dimensional datasets will prove the model’s generalization ability.
More visual insights#
More on figures

This figure visually demonstrates the effect of the Parsimonious Latent Space Model (PLSM) on latent dynamics. The left panel shows a simple 2D latent space where an agent (represented by a heart) can move in nine possible directions, including staying still. The center panel illustrates the distribution of changes in latent states (Δz) for an unconstrained model. This distribution is diffuse, indicating that the model doesn’t capture the systematic nature of the agent’s actions. The right panel shows the same distribution for the PLSM. Here, the distribution is much more concentrated, revealing the improved predictability of the latent dynamics due to regularization.

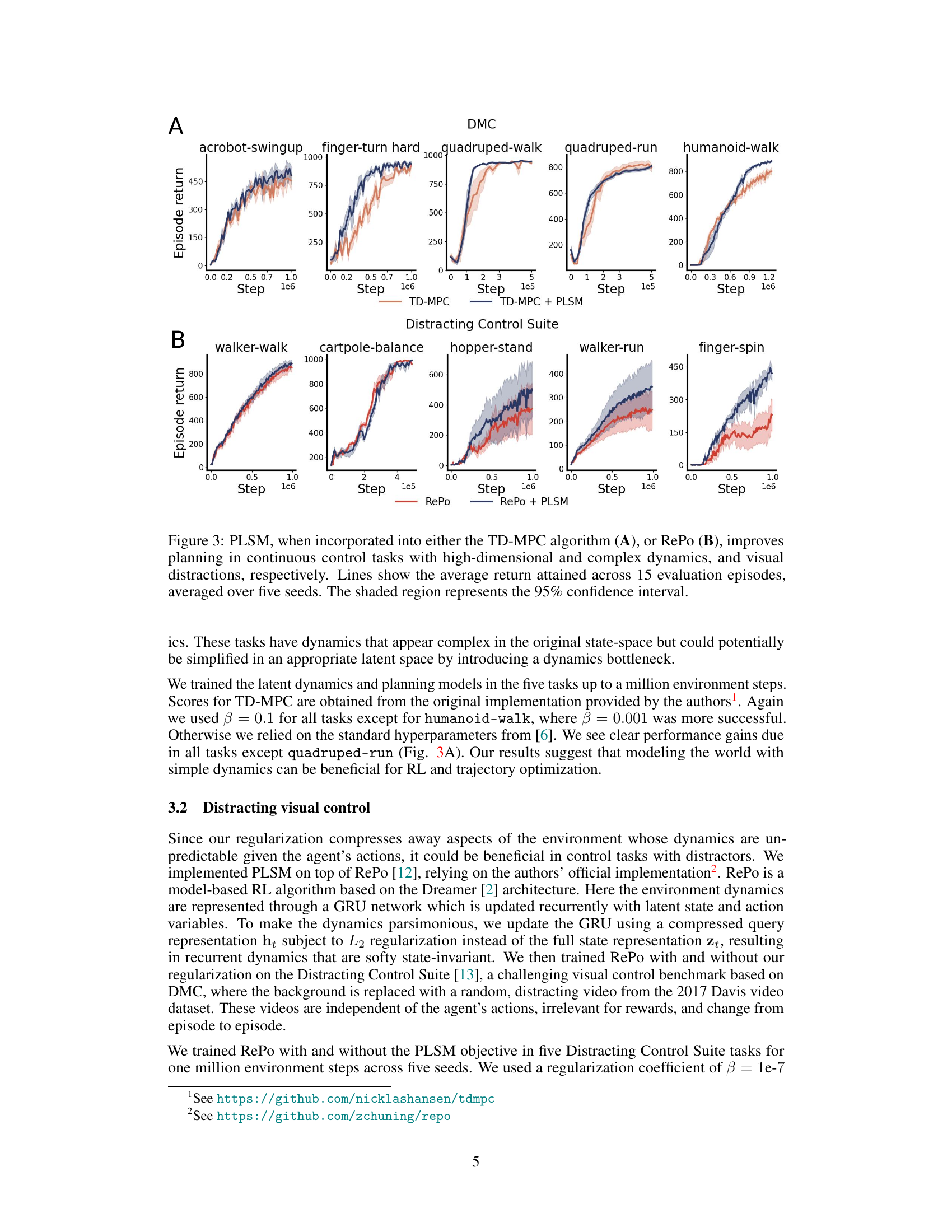
This figure displays the results of experiments comparing the performance of TD-MPC and RePo algorithms with and without the proposed PLSM method in continuous control tasks. Subfigure (A) shows results for five DeepMind Control Suite tasks, while subfigure (B) shows results for five Distracting Control Suite tasks. The y-axis represents the average episode return, while the x-axis represents the number of environment steps. Shaded areas represent 95% confidence intervals. The results demonstrate that incorporating PLSM improves the average return in most of the tasks, indicating the benefit of the proposed method for improving the efficiency and generalization of planning algorithms in complex scenarios.
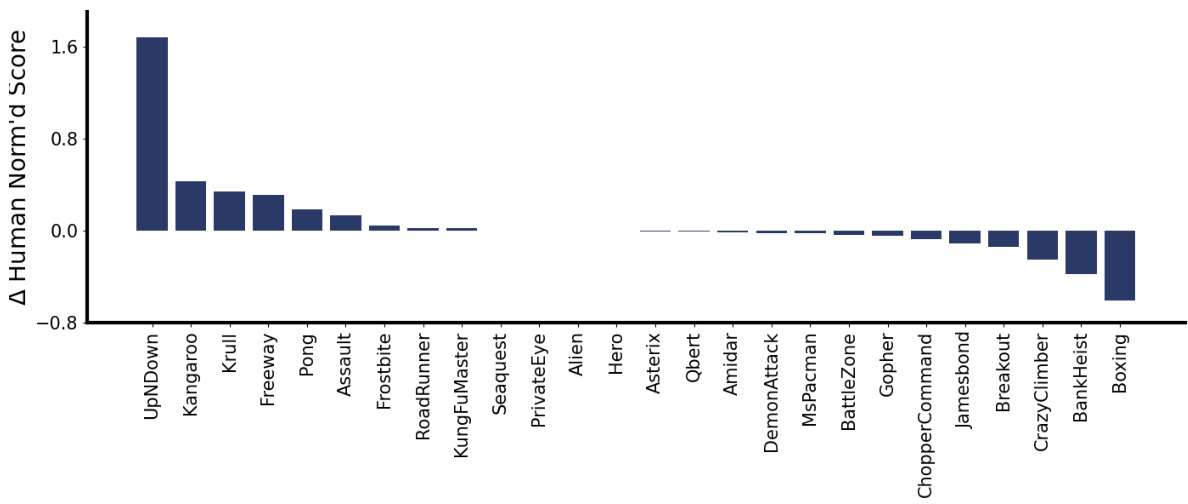
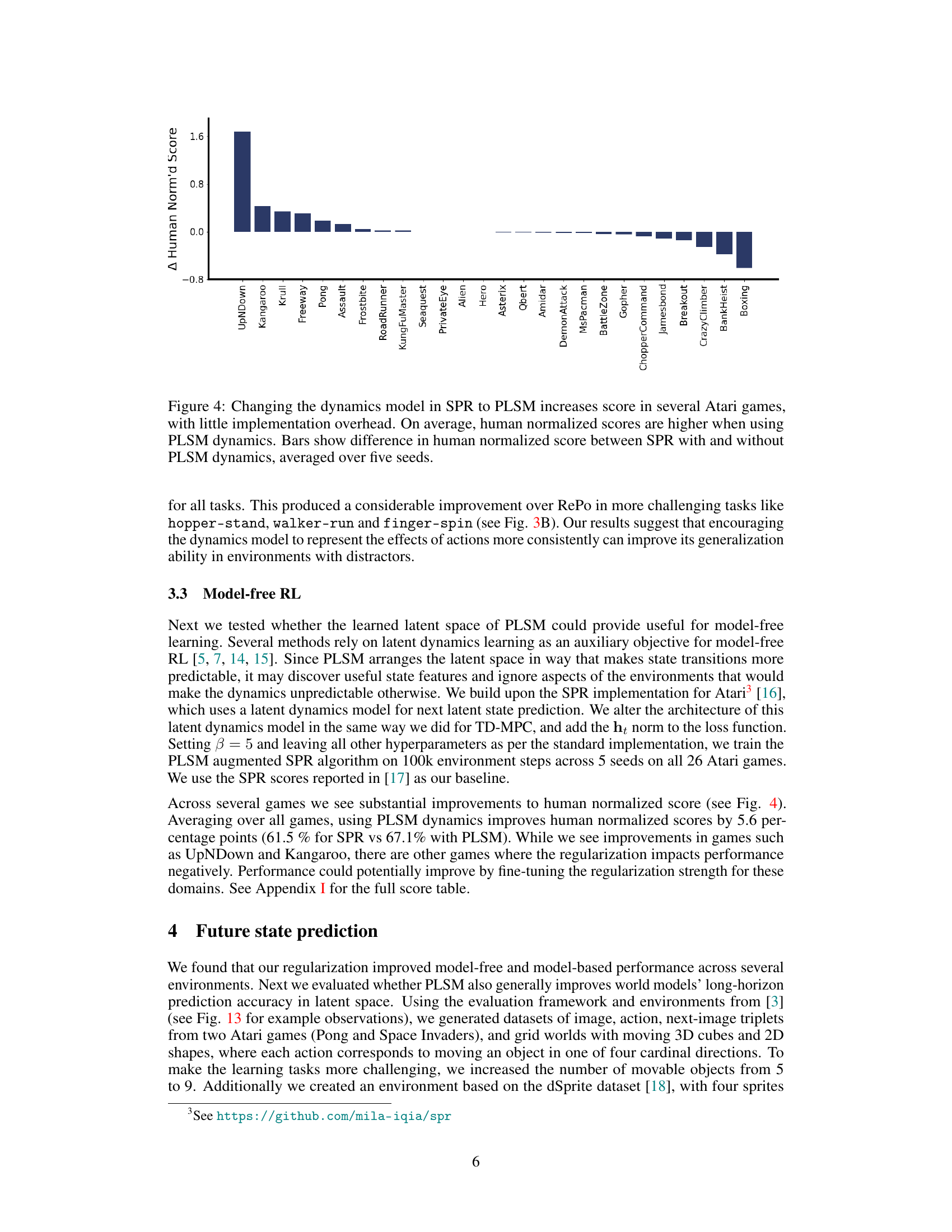
This figure shows the results of applying the Parsimonious Latent Space Model (PLSM) to several Atari games using the Self-Predictive Representations (SPR) model. The PLSM model improves the performance of the SPR model in most games, as indicated by the higher human-normalized scores. The bars in the figure show the difference in human-normalized scores between the SPR model with and without PLSM, averaged over five random seeds. The results indicate that incorporating PLSM into SPR improves the performance of the model, highlighting the effectiveness of the proposed method.
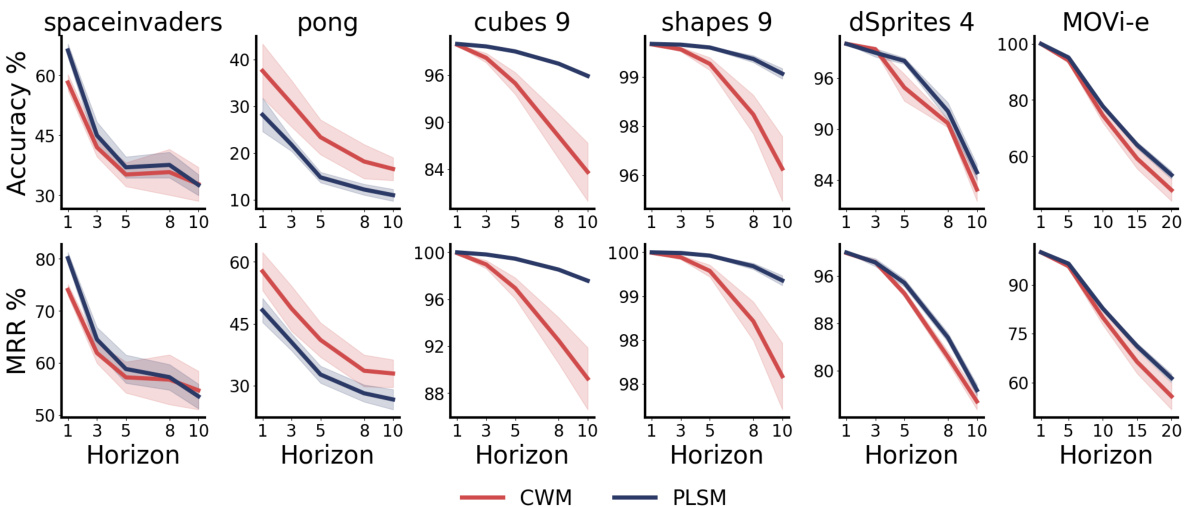
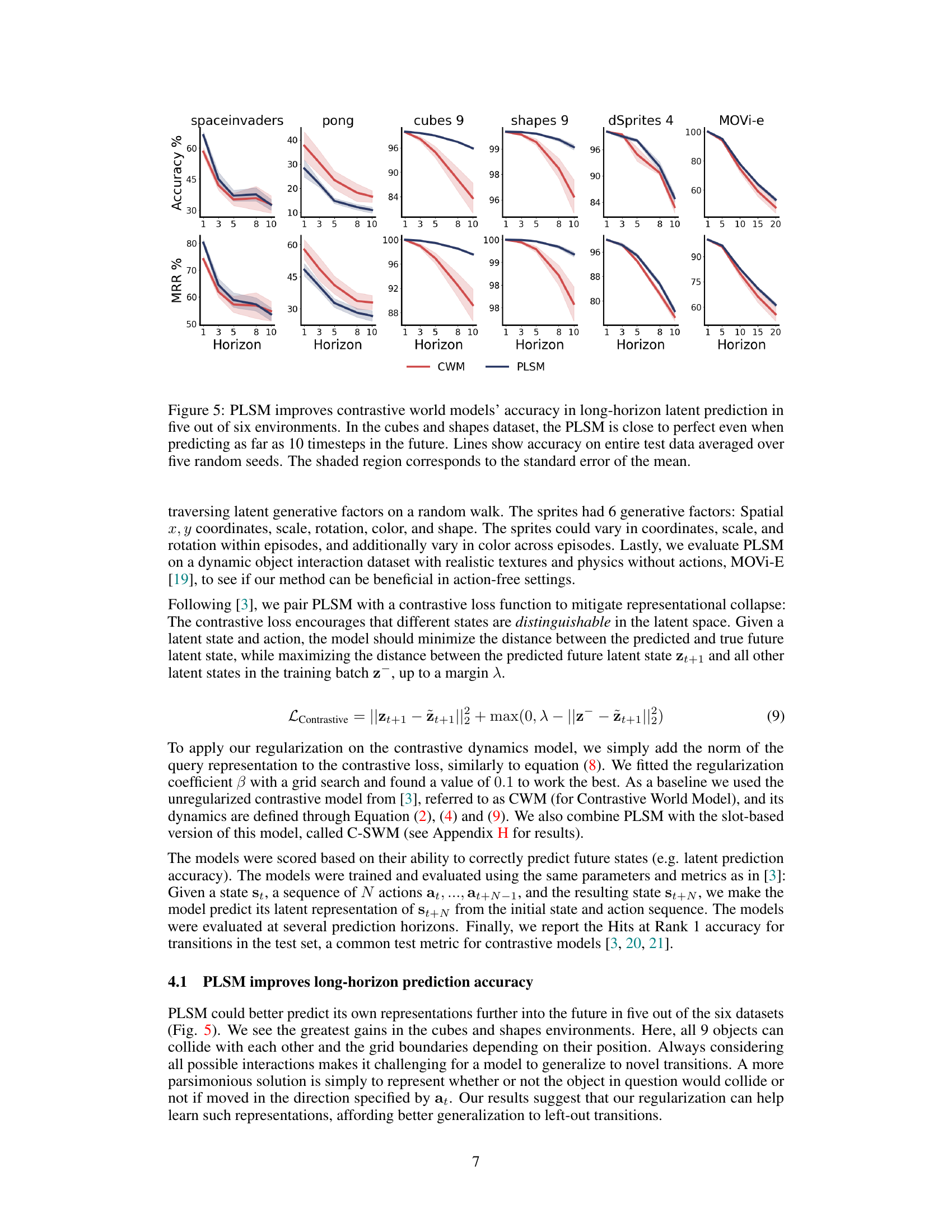
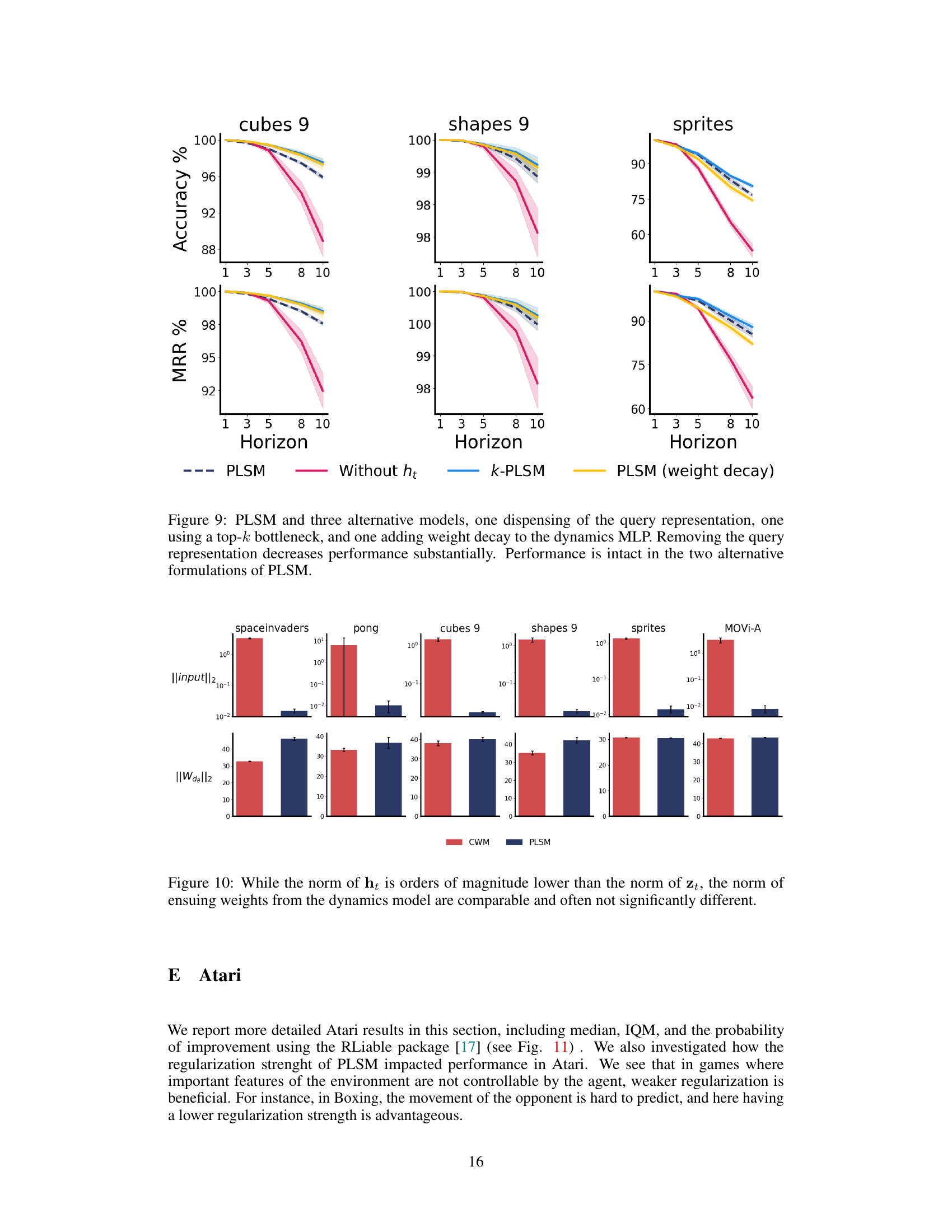
This figure compares the performance of contrastive world models (CWM) and parsimonious latent space models (PLSM) on long-horizon latent prediction tasks across six different environments. The results demonstrate that PLSM significantly improves prediction accuracy, particularly in the cubes and shapes datasets, where it achieves near-perfect accuracy even at prediction horizons of 10 timesteps. The shaded regions represent the standard error of the mean, showing the consistency of the results.

This figure compares the performance of PLSM and CWM models on generalization and robustness tests. The ‘Novel cubes’ and ‘Novel shapes’ plots show that PLSM generalizes better to unseen data with fewer objects than it was trained on, while the ‘Noise σ = 0.1’ and ‘Noise σ = 0.2’ plots demonstrate that PLSM is more robust to noisy data. The shaded areas and error bars represent confidence intervals.

This figure displays a bar chart comparing the decodability (R-squared value) of generative factors from latent states (zt), object-matched query states (when the query is conditioned on the action affecting a specific object), and query states (ht) in general. The results show that latent states (zt) have the highest decodability, meaning they retain the most information about the generative factors. Object-matched query states have intermediate decodability, while general query states (ht) have the lowest decodability. This demonstrates that the query network effectively filters out irrelevant information from the latent states, leaving only the information necessary to predict the effect of the action on the object it affects.

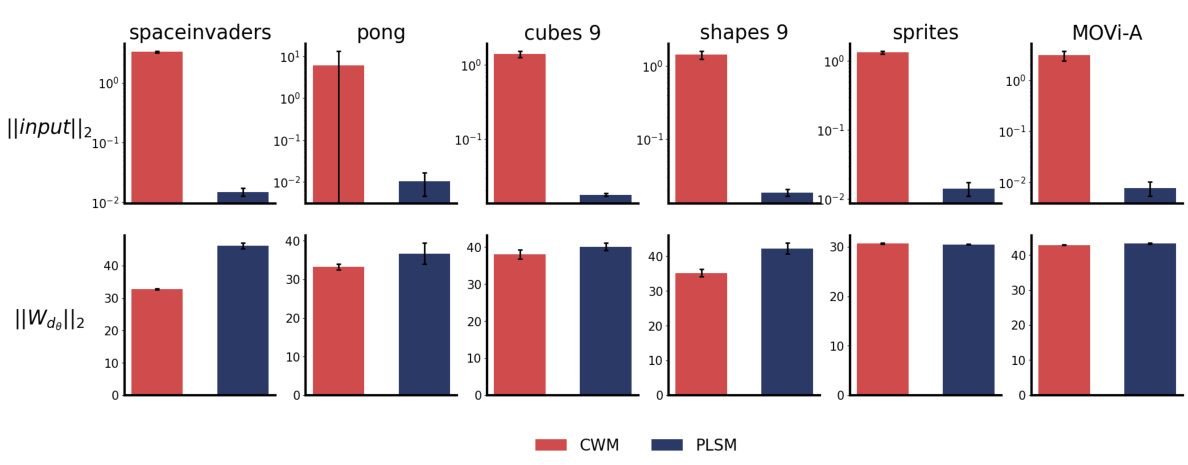
This figure compares the latent space representations learned by PLSM and two other methods that use L1 and L2 regularization. PLSM shows a more regular representation, while the others show a shrunken or distorted space. It highlights how PLSM’s mutual information minimization leads to better organization of the latent space.
This figure compares the performance of the proposed Parsimonious Latent Space Model (PLSM) against a baseline contrastive world model (CWM) in predicting future latent states. It shows that PLSM significantly improves accuracy, especially at longer prediction horizons (up to 10 timesteps), across various datasets (spaceinvaders, pong, cubes with 9 objects, shapes with 9 objects, dSprites with 4 factors, and MOVi-e). The results demonstrate PLSM’s effectiveness in learning more predictable and generalizable latent dynamics.
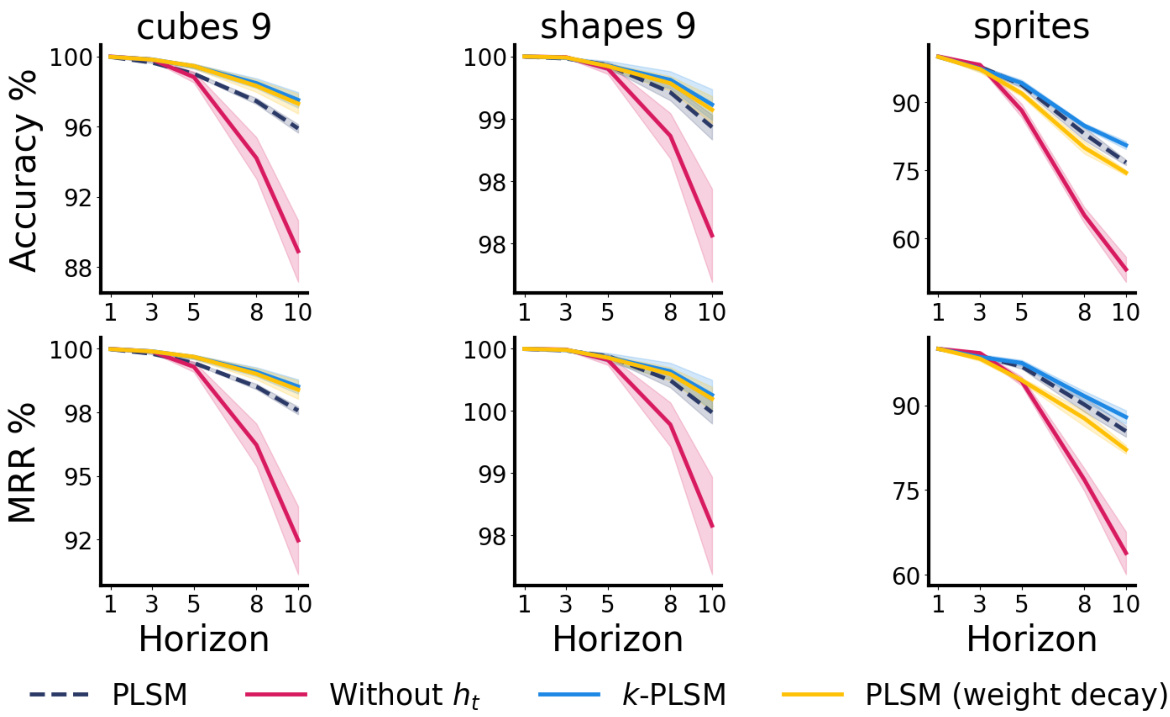
This figure displays the results of long-horizon latent prediction experiments comparing the performance of the Parsimonious Latent Space Model (PLSM) against a standard contrastive world model (CWM) across six different environments. The results show that PLSM significantly improves prediction accuracy, particularly in the cubes and shapes environment, where it achieves near-perfect accuracy even when predicting 10 timesteps into the future. The figure plots the accuracy across different prediction horizons for each environment, with error bars representing the standard error of the mean across five random seeds.

This figure shows the results of experiments comparing the performance of TD-MPC and RePo algorithms with and without PLSM in continuous control tasks. Panel A displays results for TD-MPC across five different DeepMind Control Suite environments, demonstrating the improvement in average return achieved by using PLSM. Panel B shows similar results for RePo across a different set of environments, which also include distracting visual elements. The shaded areas represent 95% confidence intervals, highlighting the statistical significance of the observed performance differences.

This figure shows the results of using PLSM with two different model-based RL algorithms, TD-MPC and RePo. The x-axis represents the number of steps, and the y-axis represents the average return across five different runs of each experiment. The shaded regions indicate the 95% confidence interval. In both (A) and (B), PLSM improves the performance of the respective baseline algorithm across a variety of tasks. The results indicate that PLSM enhances the ability of these algorithms to learn effective policies in continuous control environments with complex dynamics and visual distractions.

This figure shows an overview of the proposed architecture and results. The architecture consists of a world model with a query network that extracts a sparse representation for predicting latent transition dynamics. Three sets of RL benchmarks show performance improvements when combining the proposed method with contrastive learning, planning, and model-free RL. The lines and bars in the graphs represent the mean performance, with error bars indicating the 95% confidence interval.

This figure compares the long-horizon prediction accuracy of contrastive world models with and without the proposed PLSM method across six different environments. The results demonstrate that PLSM significantly improves accuracy, particularly in the cubes and shapes dataset, where it achieves near-perfect accuracy even when predicting 10 time steps into the future. Error bars represent the standard error of the mean, indicating confidence in the results.

The figure shows the performance of contrastive world models with and without parsimonious latent space model (PLSM) regularization on six different datasets. The x-axis represents the prediction horizon (how many steps into the future the model is predicting), and the y-axis represents the accuracy of the prediction. For most datasets, PLSM improves accuracy, particularly for longer prediction horizons. The error bars indicate the standard error of the mean.
More on tables

This table shows the accuracy of latent prediction at a horizon of 10 steps for both PLSM with slots and the baseline C-SWM model. The results are averaged over five different random seeds, with the standard error of the mean included to represent the variability of the results. The higher accuracy of PLSM with slots demonstrates its improved ability to predict future states.

This table lists the hyperparameters used for training the contrastive model, including the number of hidden units, batch size, number of hidden layers in the MLP, latent dimensions, query dimensions, regularization coefficient, margin, learning rate, activation function, and optimizer.
This table presents the accuracy of latent prediction at a horizon of 10 steps for both PLSM with slots and the contrastive world model (C-SWM). The results are averaged over five random seeds, and error bars representing the standard error of the mean are included. The table highlights the superior performance of PLSM in this specific task.
Full paper#